Интегрирование функций комплексной переменной

1. ИНТЕГРИРОВАНИЕ ФУНКЦИЙ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ

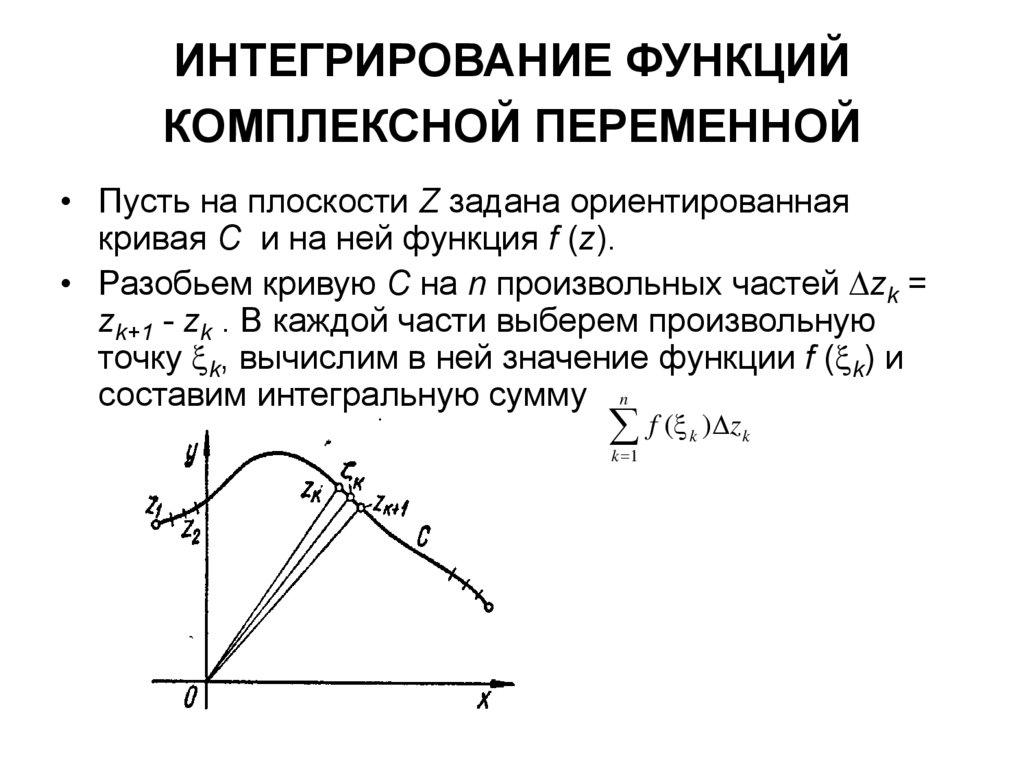
• Пусть на плоскости Z задана ориентированная
кривая С и на ней функция f (z).
• Разобьем кривую С на n произвольных частей zk =
zk+1 - zk . В каждой части выберем произвольную
точку k, вычислим в ней значение функции f ( k) и
составим интегральную сумму n
f ( ) z
k 1
k
k

2.

• Интегралом от функции f (z) вдоль кривой (контура)
С называется предел интегральной суммы
f ( z)dz
C
n
lim
max z k 0
f ( ) z
k 1
k
k
если он существует и не зависит от способа
разбиения и выбора точек внутри каждой
элементарной части.
• Если f (z) — кусочно-непрерывная функция, а
кривая С — кусочно-гладкая кривая, то интеграл
всегда существует.

3.

• Очевидно, что
zk = xk + iyk, xk = xk+1 - xk, yk = yk+1 - yk .
• Поэтому
n
n
n
k 1
n
k 1
k 1
f ( k ) z (u k iv k )( xk i yk ) (uk xk vk yk i(u k yk vk xk ))
n
(u k xk vk y k ) i (u k y k vk xk )
k 1
k 1
• После перехода к пределу при max| zk|→ 0
получаем сумму криволинейных интегралов от
действительных функций действительных
переменных.
f ( z)dz (udx vdy) i (udy vdx)
C
C
C

4.

• Некоторые свойства

5.

• Рассмотрим интеграл с переменным верхним пределом от
аналитической функции в односвязной области
z
f ( )d F ( z )
z0
• Теорема о производной интеграла по верхнему
пределу. Производная от интеграла по его верхнему
пределу равна подынтегральной функции
F ( z ) f ( z )
• Иными словами: интеграл с переменным верхним пределом
является первообразной для подынтегральной функции в
односвязной области.
• Любая аналитическая в односвязной области функция имеет в
ней первообразную.
• F(z) имеет производную в любой точке области определения,
следовательно, является в ней аналитической.

6.

• Для комплексной функции определяется и
неопределенный интеграл как совокупность
первообразных
f ( z )dz F ( z ) c
с = const.
• Если функция f (z) аналитична в односвязной
области D, то имеет место формула НьютонаЛейбница
z2
z
f ( z )dz F ( z ) z 2 F ( z 2 ) F ( z1 )
z1
1
z1,z2 D
• Если функции f (z) и g (z) – аналитические в
односвязной области D, то имеет место формула
интегрирования по частям:
z2
z2
f ( z)g ( z)dz f ( z) g ( z) f ( z)g ( z)dz
z2
z1
z1
z1

7. Способы нахождения интегралов

• Первый способ. Вычисление интегралов от непрерывной
функции путем сведения к криволинейным интегралам от
функций действительных переменных:
f ( z)dz (udx vdy) i (udy vdx)
C
C
C
• Второй способ. Вычисление интегралов от непрерывной
функции путем сведения к определенному интегралу в случае
параметрического задания пути интегрирования.
f ( z )dz f ( z (t )) z (t )dt
C
- записать параметрическое уравнение кривой z = z(t) и из него
определить пределы интегрирования.
- найти дифференциал комплекснозначной функции z(t): dz = z'(t)dt
- подставить z(t) в подынтегральное выражение, преобразовать
интеграл к виду
f ( z (t )) z (t )dt (t )dt

8.

• Третий способ. Вычисление интегралов от аналитических
функций в односвязных областях - применение формулы
Ньютона-Лейбница
z2
z
f ( z )dz F ( z ) z 2 F ( z 2 ) F ( z1 )
z1
1

9. Интеграл типа Коши

• Пусть C - любая кусочно-гладкая ориентированная
кривая, (z) - непрерывная функция, определенная
вдоль C. Интегралом типа Коши называется
выражение
1 ( z )
dz F ( z0 )
2 i C z z0
• Интеграл типа Коши есть аналитическая функция для
всех z0 C.
• т.е. на классе непрерывных функций комплексного
переменного строится класс аналитических функций

10.

• Производная интеграла типа Коши определяется по
формуле
1
( z )
F ( z0 )
dz
2
2 i C ( z z0 )
• Теорема. Если однозначная функция комплексного
переменного имеет всюду в области первую
производную, то она имеет в этой области и
производные всех высших порядков.
• Производная порядка n от интеграла типа Коши
определяется по формуле
F ( n ) ( z0 )
n!
( z )
dz
n 1
2 i C ( z z0 )

11.

• Доказательство. Пусть есть произвольный круг, не имеющий
общих точек с кривой C (z - z0 0). Функция
( z , z0 )
( z )
z z0
• непрерывна на множестве точек {z C, z0 } и имеет на нем
непрерывную частную производную
d
( z )
dz0 ( z z0 ) 2
• Значит можно провести дифференцирование F(z0) под знаком
интеграла и производная будет непрерывна и аналитична вне C :
1
( z )
F ( z0 )
dz
2
2 i C ( z z0 )
• Рассуждая аналогично, вторая производная будет иметь вид
F ( z0 )
• И т.д.
1 2
( z )
dz
3
2 i C ( z z0 )

12.

• Теорема Коши. В односвязной области D интеграл от
аналитической функции, взятый по любому кусочногладкому замкнутому контуру, принадлежащему D,
равен нулю.
f ( z)dz 0
C
Доказательство. Из аналитичности функции следует
выполнение условий д`Аламбера-Эйлера и непрерывность
частных производных
f ( z)dz (udx vdy) i (udy vdx)
C
C
C
Воспользуемся формулой Грина
v u
(
udx
vdy
)
C
D x y dxdy 0
v u
(
udy
vdx
)
C
D y x dxdy 0

13.

• Следствие. Если функция f (z) аналитична в
односвязной области D, то комплексный интеграл от
такой функции по кривой, соединяющей точки z0 и z,
не зависит от формы пути интегрирования.
• Такой интеграл можно записать в виде интеграла с переменным
верхним пределом z
f ( )d F ( z )
z0
• В многосвязной области теорема Коши, вообще говоря, не
имеет места.

14.

• Пример. Функция f(z)=1/z аналитична в кольце 0,5<|z|<2.
Возьмем в этой двусвязной области замкнутый контур С —
окружность |z|=1 и на нем две точки z1 = - 1 и z2 = 1. Вычислим
интегралы по кривым С1 и С2, где С1 — верхняя, и С2 — нижняя
полуокружности.
На окружности С имеем |z| = 1, z = ei , dz= iei d .
dz
ie i d
C z ei id i
1
0
0
dz
ie i d
C z ei id i
2
0
0

15.

• Теорема Коши для многосвязной области
Пусть функция f (z) аналитична в многосвязной
области D и непрерывна в замкнутой многосвязной
области D и пусть кривая С — составная граница
этой области. Тогда, если при интегрировании вдоль
С эту границу проходить так, что область D будет
всегда расположена по одну сторону, то интеграл от
функции f (z) вдоль границы С будет равен нулю.
• Сложный контур многосвязной области состоит из внешнего
контура Г и внутренних С1 , С2, С3, контуры попарно не
пересекаются, обход границы – положительный. Проведем в
области разрезы так, чтобы получились 2 односвязные области.

16.

• Следствия из теоремы.
1. При выполнении условий теоремы интеграл по внешнему
контуру равен сумме интегралов по внутренним; обход на всех
контурах в одну сторону
n
f ( z )dz f ( z )dz
k 1C k
Г
2. Если f(z) является аналитической в односвязной области D и на
границе области, за исключением, быть может, точки а этой
области, то интегралы по различным замкнутым кривым,
которые лежат в области D и ограничивают области,
содержащие точку а, равны между собой:
f ( z )dz f ( z )dz
Ck
Cm

17. Интегральная формула Коши

• Устанавливает связь между значениями аналитической функции
в любой внутренней точке области со значениями этой функции
на контуре, охватывающем эту точку.
• Теорема. Если функция f(z) является аналитической
в области D и на ее границе, то для любой
внутренней точки z0(z0 D) имеет место равенство
f ( z0 )
1
f ( z)
dz
2 i C z z0
• Область D может быть односвязной или многосвязной, а
граница области - простым или сложным контуром.
• Этот интеграл называется интегралом Коши.
• Отличия от интеграла типа Коши: функция аналитическая, а не
непрерывная, контур замкнутый, а не произвольный
• Подынтегральная функция непрерывна на границе

18.

• Для интеграла Коши сохраняются свойства интеграла
типа Коши
1. Аналитическая функция в любой точке аналитичности
может быть записана в виде интеграла
f ( z0 )
1
f ( z)
dz, z 0 D
2 i C z z 0
2. Аналитическая функция имеет производные любого
порядка, для которых справедлива формула
f (n) ( z0 )
n!
f ( z)
dz
n 1
2 i C z z 0
• В окрестности каждой точки z0, где существует
производная, функция f(z) может быть представлена
сходящимся рядом (рядом Тейлора):
f ( z 0 )
f (n) ( z 0 )
2
f ( z ) f ( z 0 ) f ( z 0 )( z z 0 )
( z z 0 ) ...
( z z 0 ) n ...
2!
n!

19. Правила вычисления интегралов по замкнутому контуру от функций комплексного переменного

1.
( z )
( z ) dz
Будем рассматривать интегралы вида C
, где функция
D
(z) аналитическая
в , а (z) - многочлен, не имеющий
нулей на контуре С.
В области D нет нулей многочлена (z). Тогда f(z)- функция
аналитическая, применяем основную теорему Коши
f ( z )dz 0
C
2.
В области D расположен один простой нуль z = a многочлена
(z). Тогда записываем дробь в виде ( z ) f ( z )
, где f(z) ( z) z a
функция аналитическая в D.
Применяем интегральную формулу Коши
( z )
f ( z)
dz
( z )
z a dz 2 i f (a)
C
C

20.

3. В области D расположен один кратный нуль z = а многочлена (z)
( z )
(кратности n). Записываем дробь в виде
, f ( z)
( z ) ( z a) n
где f(z)- функция, аналитическая в D.
f ( z)
2 i
( n 1)
dz
f
(a)
n
n 1 !
C z a
4. В области D расположены несколько нулей многочлена (z): zi = аi
Используя следствие 1 из теоремы Коши для многосвязной
области, запишем интеграл в виде суммы
k
f ( z )dz f ( z )dz
C
i 1
Ci
где Сi - границы непересекающихся окрестностей точек zi . Для
каждого из полученных интегралов проводим вычисления
отдельно