Похожие презентации:
Контурные интегралы функций комплексного переменного (ФКП)
1.
Лекция 6Контурные интегралы ФКП
2.
«…très souvent les lois particulières déduites parles physiciens d'un grand nombre d'observations
ne sont pas rigoureuses, mais approchées.»
«… very often the laws derived by physicists from
a large number of observations are not rigorous,
but approximate.»
Augustin Louis Cauchy (1789-1857)
2
3.
Т. (Коши для односвязной области).Пусть в замыкании односвязной области D
задана однозначная аналитическая функция f(z).
Тогда для любого замкнутого контура ∂Ω D
Доказательство.
3
4.
Применим формулу Грина:5.
ПолучимC учетом условий КРЭД
u v u
v
x
x y y
теорема доказана.
5
6.
Обобщения теоремы КошиТ. (вторая ф-ка т. Коши) Если функция f(z)
является АФ в односвязной области Ω,
ограниченной кусочно-гладким контуром ∂Ω и
непрерывна на замыкании Ω, то
Следствие. Если f(z) – АФ в односвязной
области, то интеграл от неё вдоль любой дуги не
зависит от формы дуги, а зависит только от
начальной
и
конечной
точек
пути
интегрирования.
6
7.
Следствие. (аналог ф-лы Ньютона-Лейбницадля АФ).
Если:
1) кривая интегрирования AB находится в
односвязной
области,
в
которой
подынтегральная функция аналитична;
2) первообразная Ф(z) подынтегральной функции
однозначна в этой области, то
AB
B
f ( z )dz f ( z )dz ( z ) A ( B) ( A)
B
A
7
8.
Т. (Коши для многосвязной области).Пусть f(z) является аналитической функцией в
многосвязной области Ω, ограниченной извне
контуром C0, а изнутри контурами C1, C2, … ,Cn,
и f(z) непрерывна на замыкании Ω. Тогда
где
С+
–
полная
граница
области,
ориентированная так, что область остается слева.
8
9.
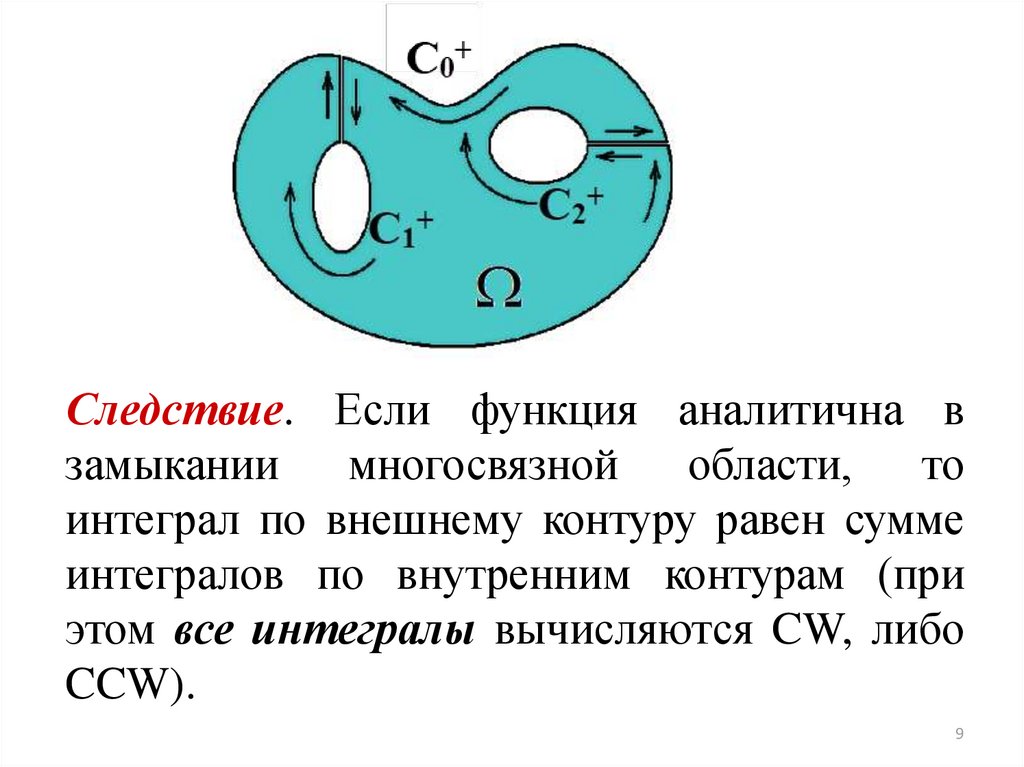
Следствие. Если функция аналитична взамыкании
многосвязной
области,
то
интеграл по внешнему контуру равен сумме
интегралов по внутренним контурам (при
этом все интегралы вычисляются CW, либо
CCW).
9
10.
П. Вычислить интегралdz
I С
z ,
C
0
где C0 – некоторый контур, внутри которого
находится точка z = 0.
10
11.
По следствию контур C0 можно заменитьокружностью С1: |z| = r достаточно малого радиуса
r, чтобы она целиком содержалась в области
ограниченной исходным контуром:
11
12.
Тогдаz rei
i
dz re id
0 2
2
0
i
2
re id
i d 2 i.
i
0
re
12
13.
П. Вычислить интегралze dz,
z
AB
где АВ – отрезок прямой, соединяющий точки
z=0 и z=1+i.
Так как f ( z ) A(C ), то
1 i
ze dz ze dz
z
AB
z
0
ze
z
1 i
0
1 i
e dz
z
0
13
14.
1 i(1 i )e
1 i
ie
e
z 1 i
0
1 i
(1 i)e
1 i
e
1
1 ie cos1 i sin1 1
1 e sin1 ie cos1.
П. Вычислить интеграл
d
w z ,
1
z
где интегрирование может совершаться по любой
линии, соединяющей точку ζ = 1 с точкой ζ = z,
не проходящей через т. ζ = 0.
14
15.
Случай 1. Вдоль пути, не окружающего нулевуюточку:
Первообразной является многозначная ф-ция
Ln z ln z i arg z 2 k , k Z .
15
16.
Для применения формулы НЛ необходимовыбрать какую-либо ветвь этой функции,
например, главную (k=0):
z
d
1 ln i arg 1
z
ln z i arg z ln 1 i arg1 ln z.
Случай 2. Путь интегрирования окружает один
раз нулевую точку.
16
17.
Эту кривую нельзя поместить в односвязную область,где подынтегральная функция аналитична. Ф-ла
Ньютона – Лейбница неприменима.
17
18.
d2 i ln z
C
Если путь интегрирования делает k оборотов в
положительном направлении, то
d
ln z 2 ki
C
Формула дает интегральное представление
функции Lnz и объясняет многозначность этой
функции.
18
19.
Т. (формула Коши, интеграл Коши).Пусть функция f(z) аналитична в замыкании
области Ω и z0 Ω – произвольная точка. Тогда
имеет место формула Коши
где C – произвольный замкнутый контур,
целиком лежащий в замыкании Ω и
содержащий точку z0 внутри себя.
19
20.
Формальное доказательство.Пусть ε – произвольное достаточно малое число,
такое, что окружность этого радиуса с центром
в точке z0 целиком лежит внутри контура C.
Подынтегральная функция аналитична в области
|z – z0| > ε. Поэтому
z z0 ei
i
dz ie d
0 2
20
21.
2f z0 e
0
e
i
i
i e
2
i
d i f z0 e
i
d
0
Переходя к пределу при ε→0, получим
ч.т.д.
21
22.
Следствие. При выполнении условий теоремыКоши АФ имеет производные любого порядка
и
Замечание. Если т. z0 лежит на контуре, то
22
23.
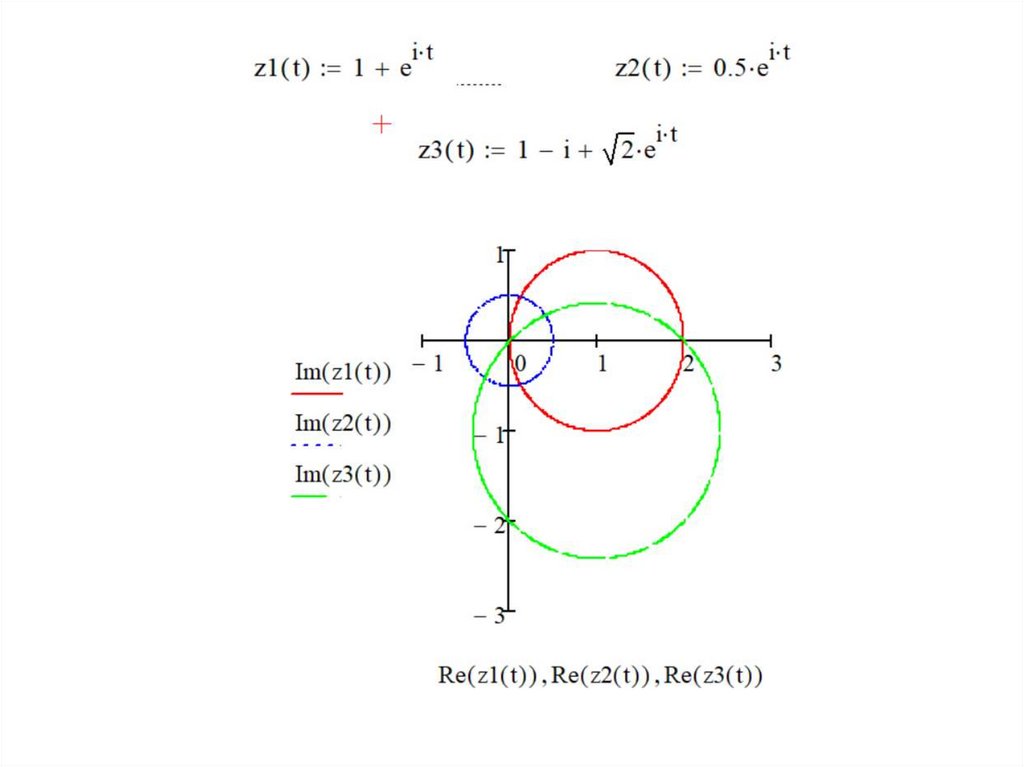
Обобщенный вариант формулы Коши:П. Вычислить
23
24.
25.
a) Перепишем интеграл в виде:26.
zze
I 2 i 2
z 1
z 1
ei
26
27.
z1 1, z2 iРазложим функцию на сумму простых дробей
z
z 1
1
.
2
2
( z 1)( z 1)
2 ( z 1) 2 ( z 1)
27
28.
( z 1) ei
z i
2
z
z i
ie
z
z 1
(1 i ) e ei.
i
28
29.
П. Вычислить2 i
I
( z sin ( z ))
2!
z 2
29
30.
i ( 2cos ( z ) z sin ( z ))z 2
2 i (cos2 sin 2).
30























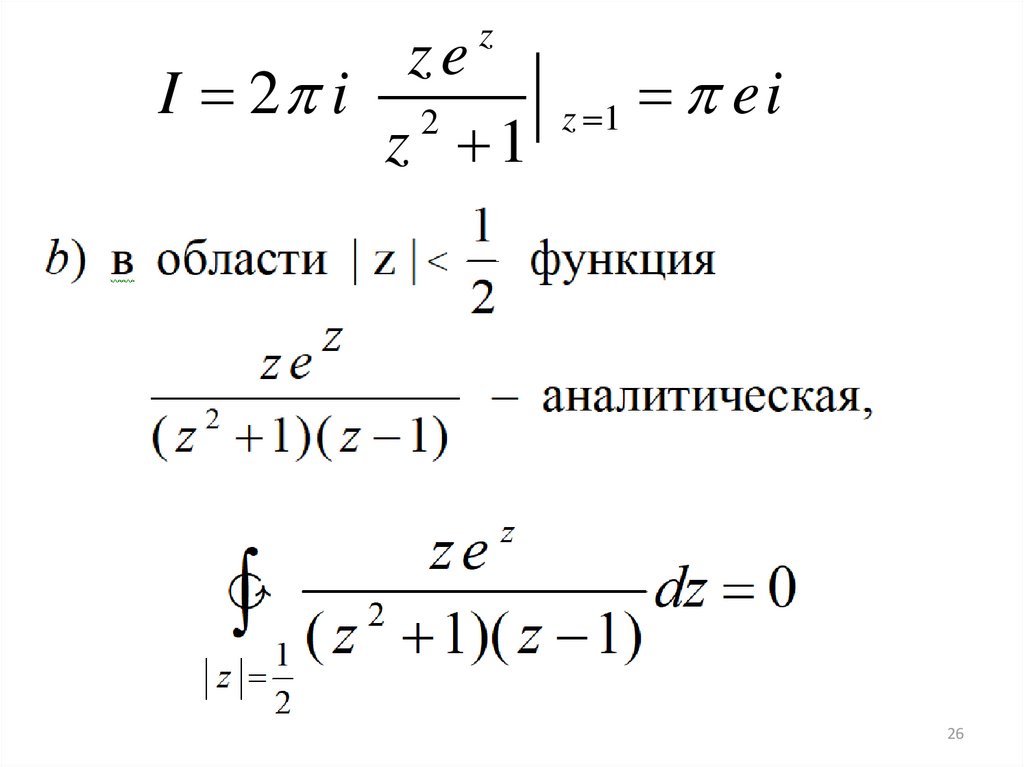

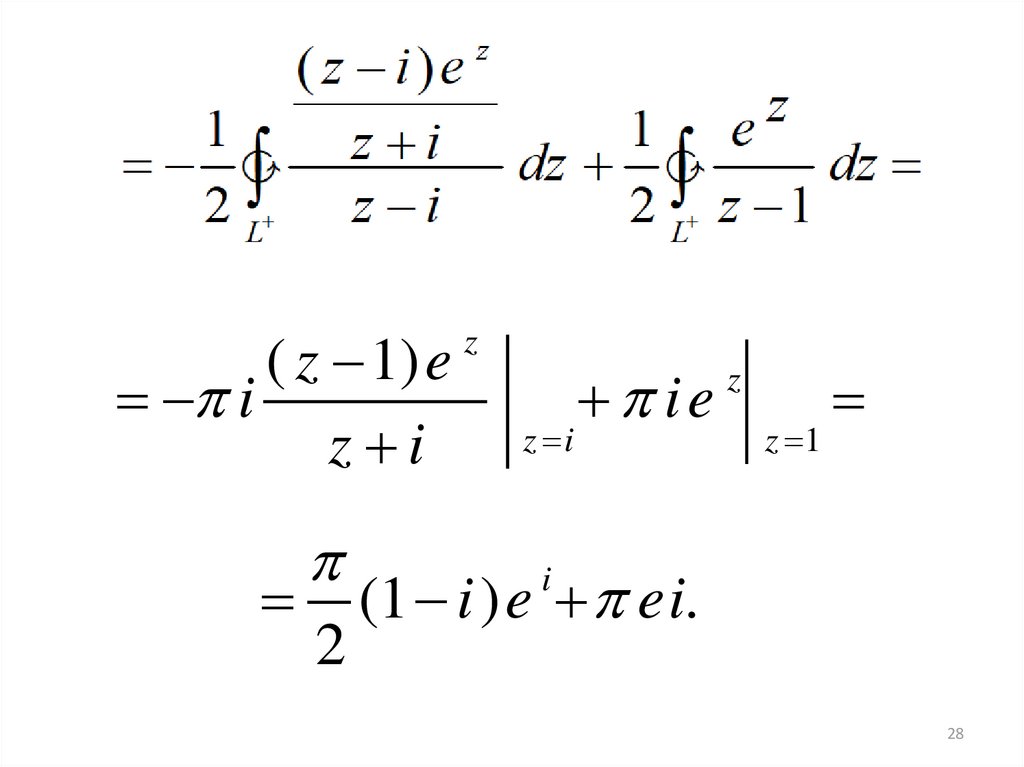
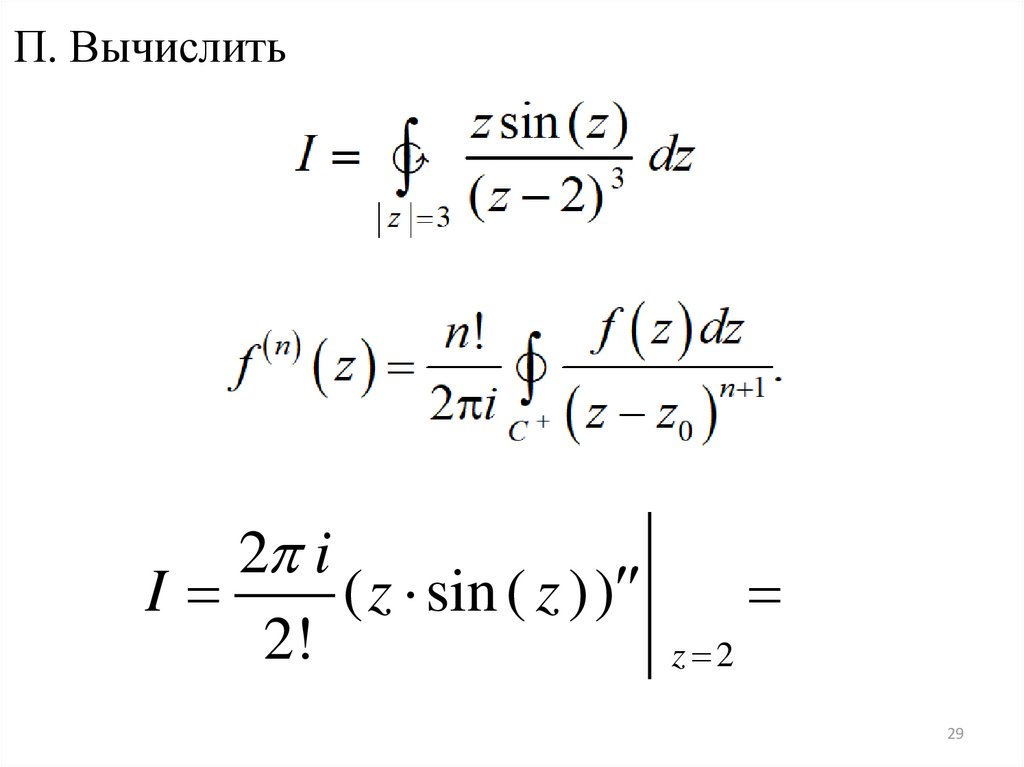
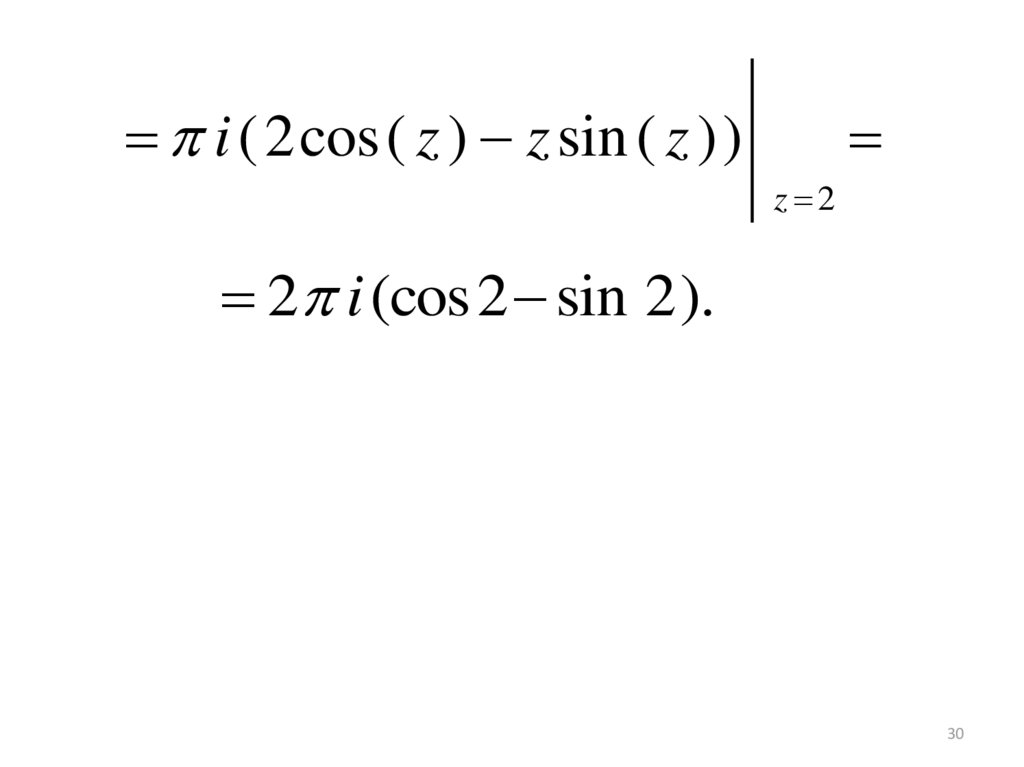
 Математика
Математика








