Похожие презентации:
Интеграл. Формула Ньютона-Лейбница. Что называют криволинейной трапецией?
1.
ИНТЕГРАЛ. ФОРМУЛАНЬЮТОНА-ЛЕЙБНИЦА
2. Здравствуйте, внимательно изучите тему, рассмотрите пример нахождения интеграла
3.
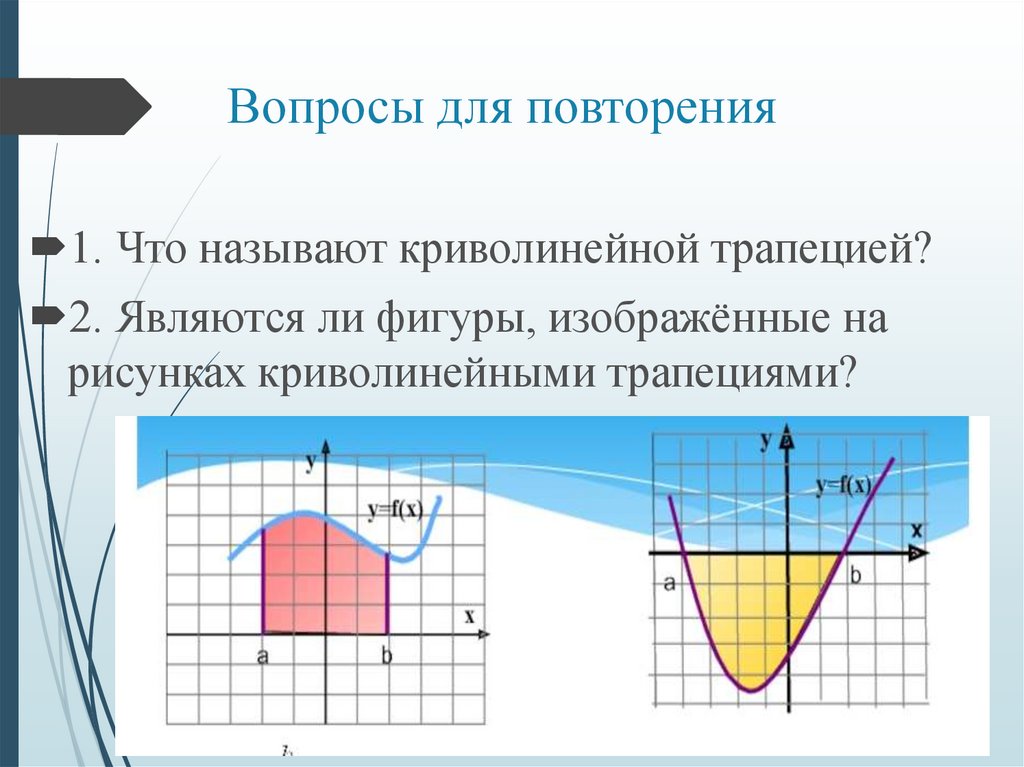
4. Вопросы для повторения
1. Что называют криволинейной трапецией?2. Являются ли фигуры, изображённые на
рисунках криволинейными трапециями?
5. 3. Запишите формулу для вычисления площади криволинейной трапеции
6. Рассмотрим другой подход к вычислению площади криволинейной трапеции
Будем считать функцию fнеотрицательной и непрерывной на
отрезке [а; в], тогда площадь S
соответствующей криволинейной
трапеции можно приближённо
подсчитать следующим образом
7.
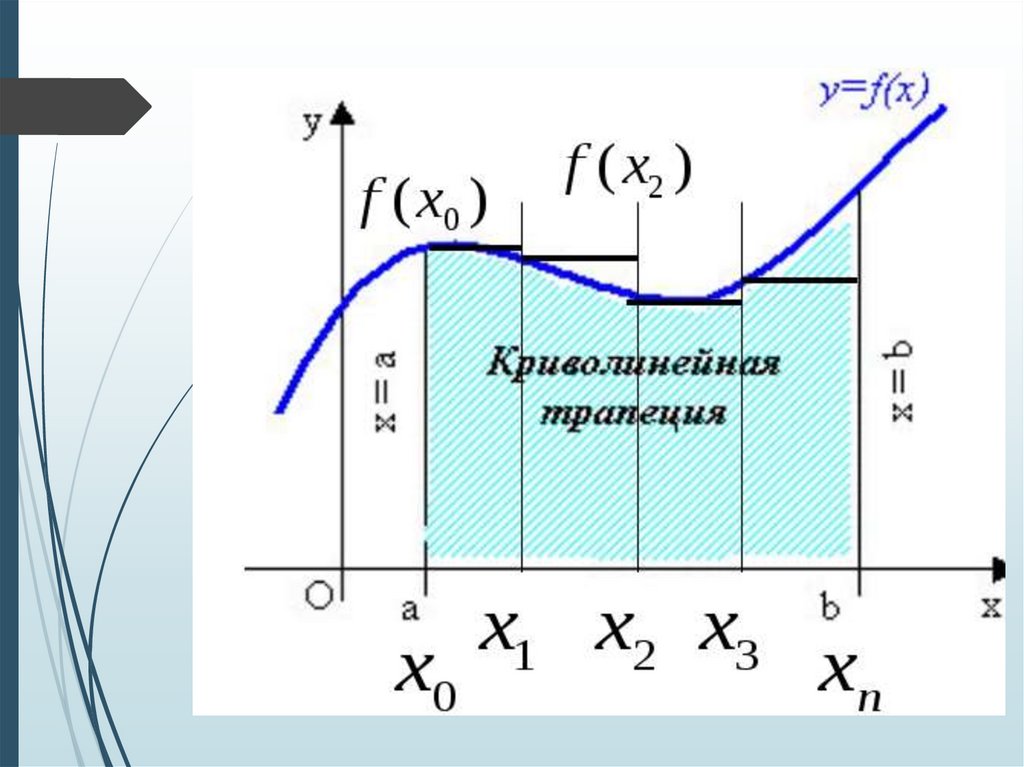
8. Разобьём отрезок [а; в] на n отрезков одинаковой длины точками
х0 а х1 х2 ... х n 1 х вn
в а
х
n
Рассмотрим
сумму
S n f ( x0 ) х f ( x1 ) х f ( x2 ) х ... f ( xn 1 ) х
( f ( x0 ) f ( x1 ) f ( x2 ) ... f ( xn 1 )) х
9. При n → ∞ Sn→ к некоторому числу
Это число называют интеграломфункции f от а до в и обозначают:
в
∫ f(х)dх
а
10.
Числа а и в - называются пределамиинтегрирования, а – нижним пределом,
в – верхним.
Знак ∫ - называют знаком интеграла
Функцию f называют подынтегральной
функцией, а переменная х – переменной
интегрирования
df- знак дифференциала
11.
Итак, если f( х ) ≥0 на отрезке [а; в], топлощадь соответствующей
криволинейной трапеции выражается
формулой:
в
S = ∫ f(х)dх
а
12.
Сравнивая формулыкриволинейных трапеций :
в
S = ∫ f(х)dх и S = F(в) – F(а)
а
Делаем вывод:
13.
Формула Ньютона-Лейбница14.
Иссак Ньютон(1643-1716)
Готфрид
Лейбниц(1646-1716).
15.
Функция f
K–
пос
тоян
ная
Общи
й
вид
первообр
аз
ных
кх
+С
F
хn
sin x
cos x
(n-целое
n≠1)
хn+1
n+ 1
+C
-cosx
+C
sin x
+C
1
1
сos2x
sin2x
tgx
+C
-ctgx
+C
1
х
2 х
16.
17. Пример:
33
3
3
х
3
2
8 1
3
2
2 х dx 3 3 3 9 3 6 3
2
2
х2
2
2
2
(
2
х
4
)
dx
(
2
4
х
)
(
2
8
)
(
1
4) 12 5 7
1
2
1
18.
22
х
dx
0
2
х dx
3
1
4
3
(5х 3)dx
1
2
0
sin 5 xdx
П
dx
2
x





![Разобьём отрезок [а; в] на n отрезков одинаковой длины точками Разобьём отрезок [а; в] на n отрезков одинаковой длины точками](https://cf3.ppt-online.org/files3/slide/f/FjAIapdYr93BSbHkvXE1RfzLMiOK6oy5mwt8N4/slide-7.jpg)








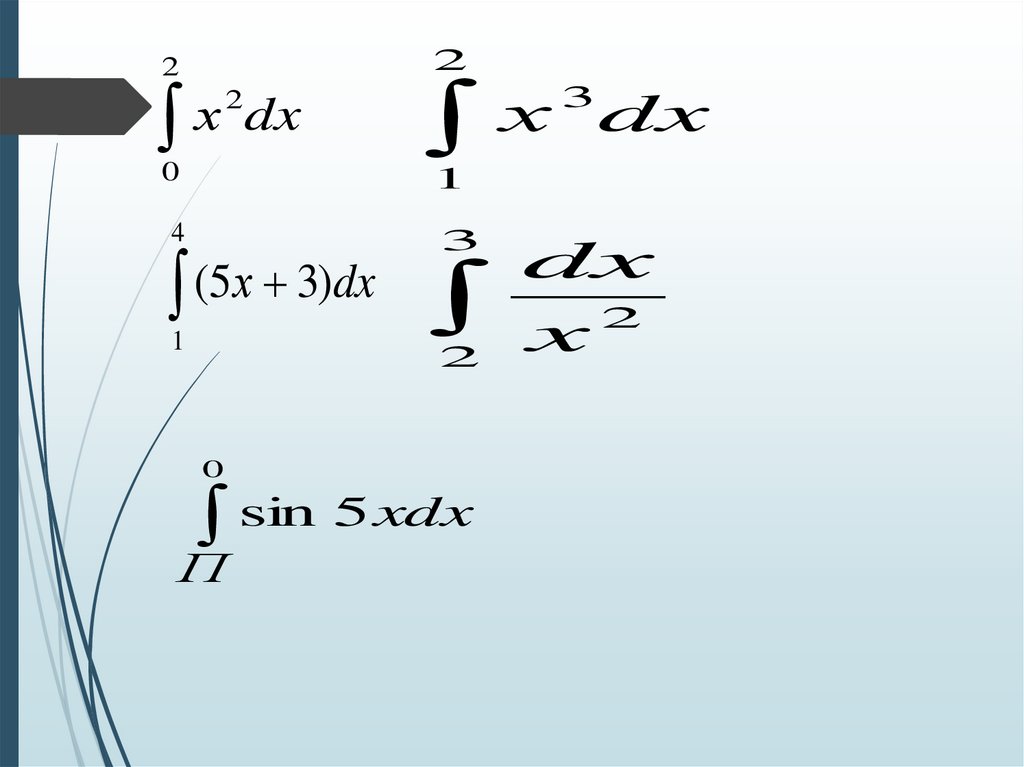

 Математика
Математика








