Похожие презентации:
Понятие потока вектора. Теорема Гаусса
1. ПОНЯТИЕ ПОТОКА ВЕКТОРА
• Рассмотрим некоторую замкнутуюповерхность в электрическом поле
E
2.
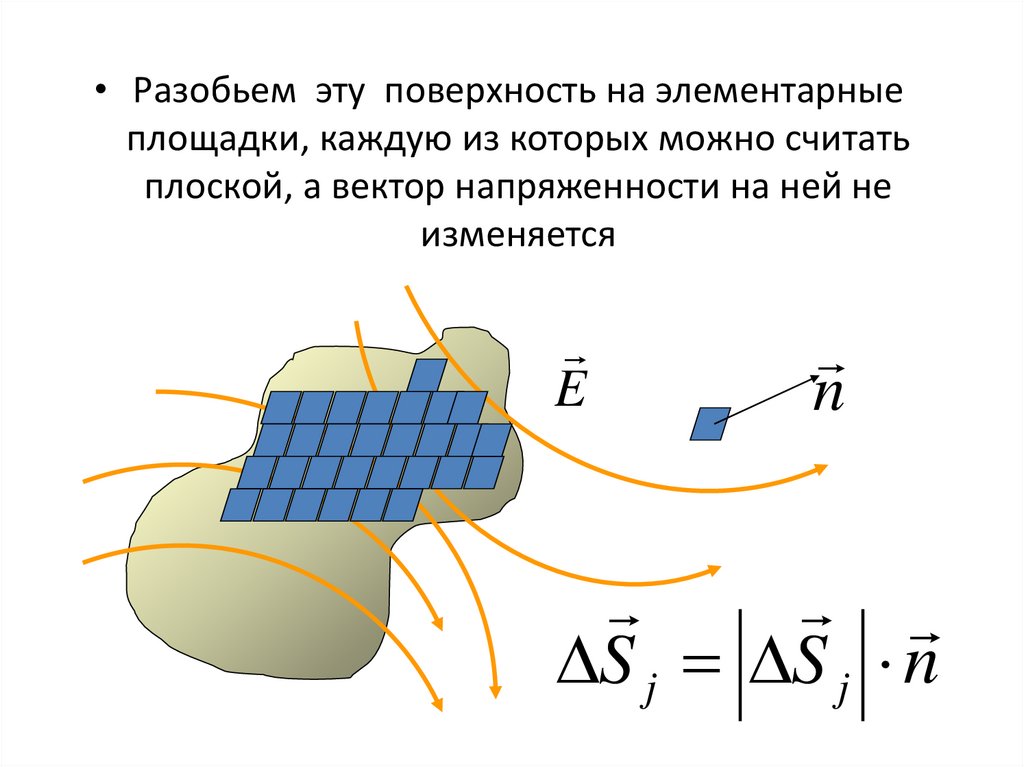
• Разобьем эту поверхность на элементарныеплощадки, каждую из которых можно считать
плоской, а вектор напряженности на ней не
изменяется
E
n
S j S j n
3. Поток вектора напряженности через площадку ∆S
j E S j E S j cosПоток вектора напряженности через всю
замкнутую поверхность S
S
E dS
4. Поле перпендикулярно площадке – поток максимальный
En
E S E S cos
E S cos 0
E S
5. Поле параллельно площадке – поток равен 0
nE
E S E S cos
E S cos 90 0
6. ТЕОРЕМА ГАУССА
7. Теорема Гаусса
• Поток вектора напряженности через любуюзамкнутую поверхность равен алгебраической
сумме зарядов, заключенных внутри данной
поверхности, поделенной на электрическую
постоянную.
qi
E dS
s
0
8. Напрерывное распределение заряда
1E dS ( x, y, z )dV
s
0
V
1
E dS ( x, y)dS
0
s
S
1
E dS (l )dl
s
0
L
9. ПРИМЕНЕНИЕ ТЕОРЕМЫ ГАУССА ДЛЯ РАСЧЕТА ЭЛЕКТРОСТАТИЧЕСКИХ ПОЛЕЙ В ВАКУУМЕ
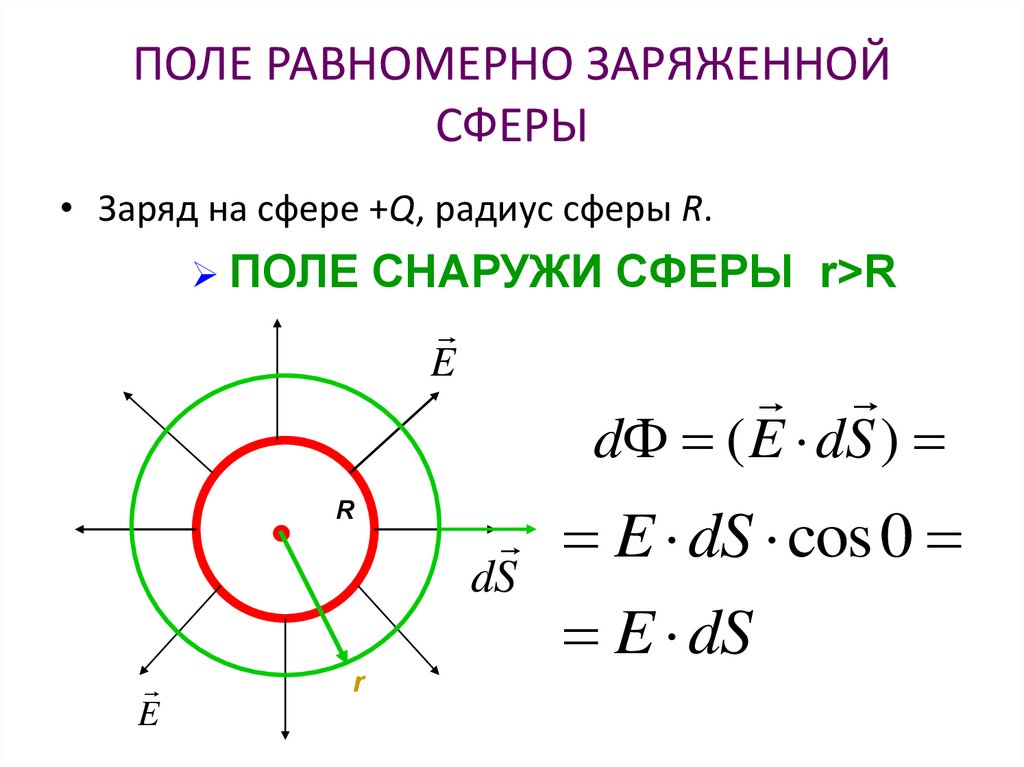
10. ПОЛЕ РАВНОМЕРНО ЗАРЯЖЕННОЙ СФЕРЫ
• Заряд на сфере +Q, радиус сферы R.ПОЛЕ
СНАРУЖИ СФЕРЫ r>R
E
R
E
r
d ( E dS )
dS
E dS cos 0
E dS
11.
qiE dS E dS
0
s
s
E - постоянна на выбранной поверхности интегрирования
E dS E dS
q Q
S
S
i
0
0
Q
dS 4 r
2
S
E 4 r
2
kQ
1
E
,
k
2
2
4 0 r
r
4 0
Q
0
12. ПОЛЕ ВНУТРИ СФЕРЫ r<R
ПОЛЕ ВНУТРИ СФЕРЫ r<Rq
i
0
R
r
0
0
Заряд расположен на внешней сфере
радиуса R, внутри сферы радиуса r
заряда нет
E dS 0
s
Q
E 0
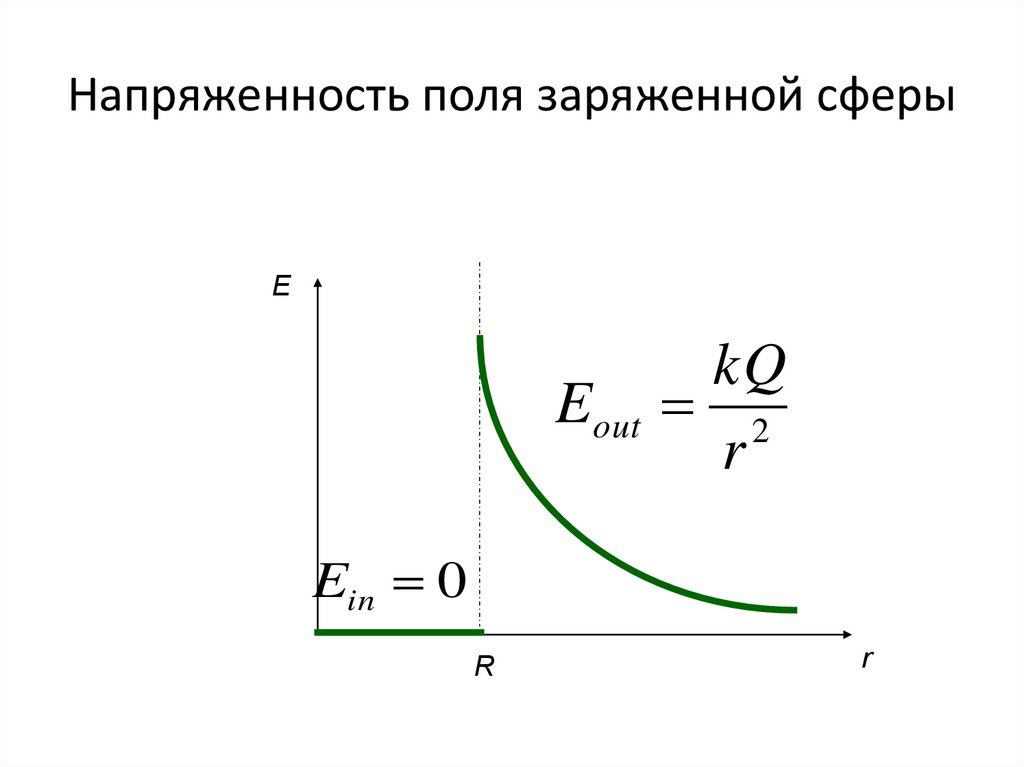
13. Напряженность поля заряженной сферы
EEout
kQ
2
r
Ein 0
R
r
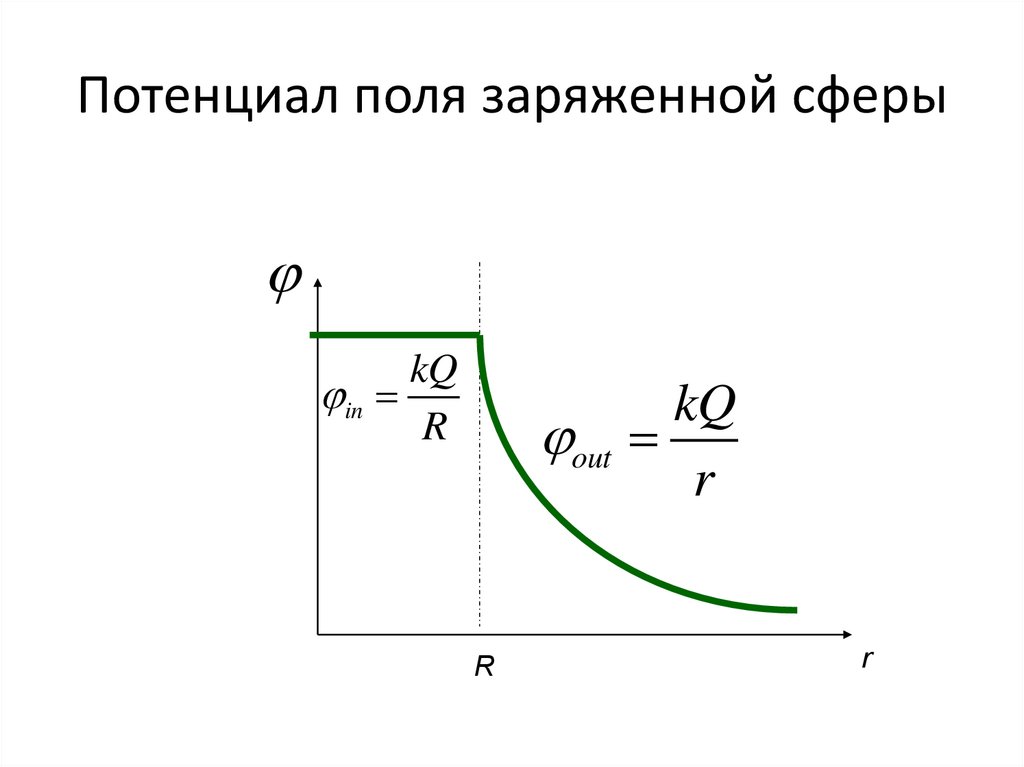
14. Потенциал поля равномерно заряженной сферы
Ein 0Eout
kQ
2
r
in Ein dr 0 const1
kQ
out Eout dr 2 dr
r
kQ
const 2
r
15.
• Одна из констант выбирается произвольно• Определяет начало отсчета
• Вторая – из условия непрерывности потенциала
на границе областей
in (r R) = out (r R)
r , out (r ) 0
const 2 0
16.
условие непрерывности потенциалана границе областей
kQ
const1
const 2
R
kQ
const1
R
17. Потенциал поля сферы
kQin R , r R
kQ , r R
out
r
18. Потенциал поля заряженной сферы
kQin
R
out
R
kQ
r
r
19. ПОЛЕ РАВНОМЕРНО ЗАРЯЖЕННОГО ШАРА
• Объемная плотность заряд шара + , радиусR.
ПОЛЕ СНАРУЖИ шара r>R
АНАЛОГИЧНО
ПОЛЮ СНАРУЖИ
СФЕРЫ
4 3
R
Q
3
E
=
2
2
4 0 r
4 0 r
R
3 0 r 2
3
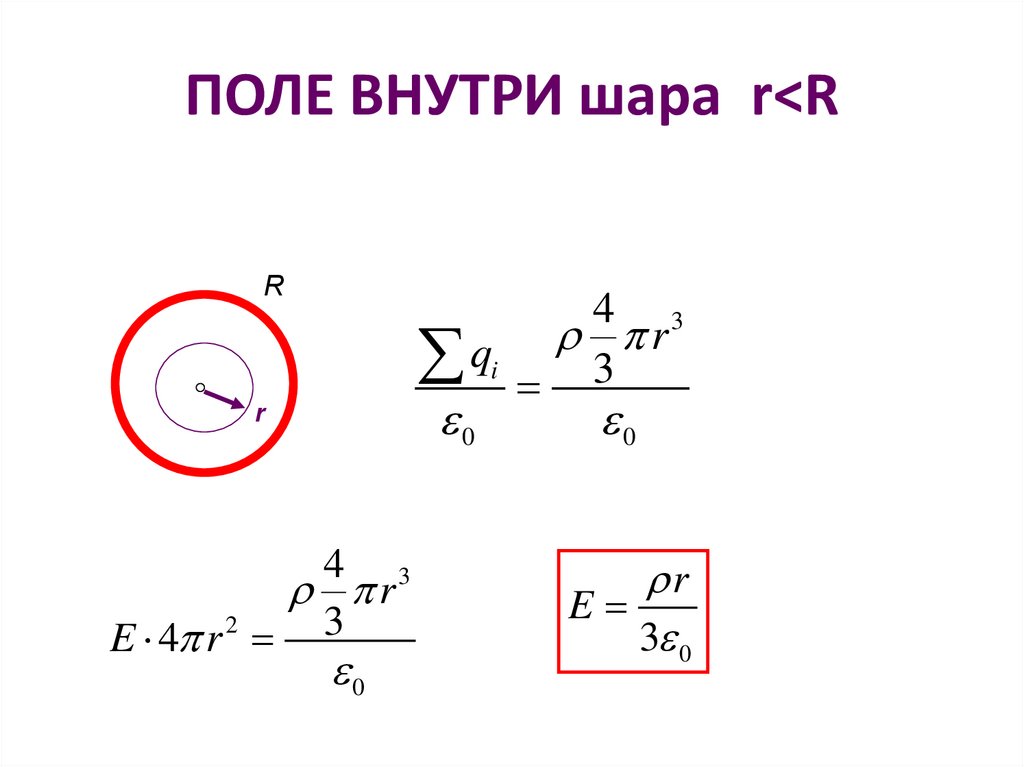
20. ПОЛЕ ВНУТРИ шара r<R
ПОЛЕ ВНУТРИ шара r<RR
4 3
r
q
i 3
0
r
4 3
r
E 4 r 2 3
0
0
r
E
3 0
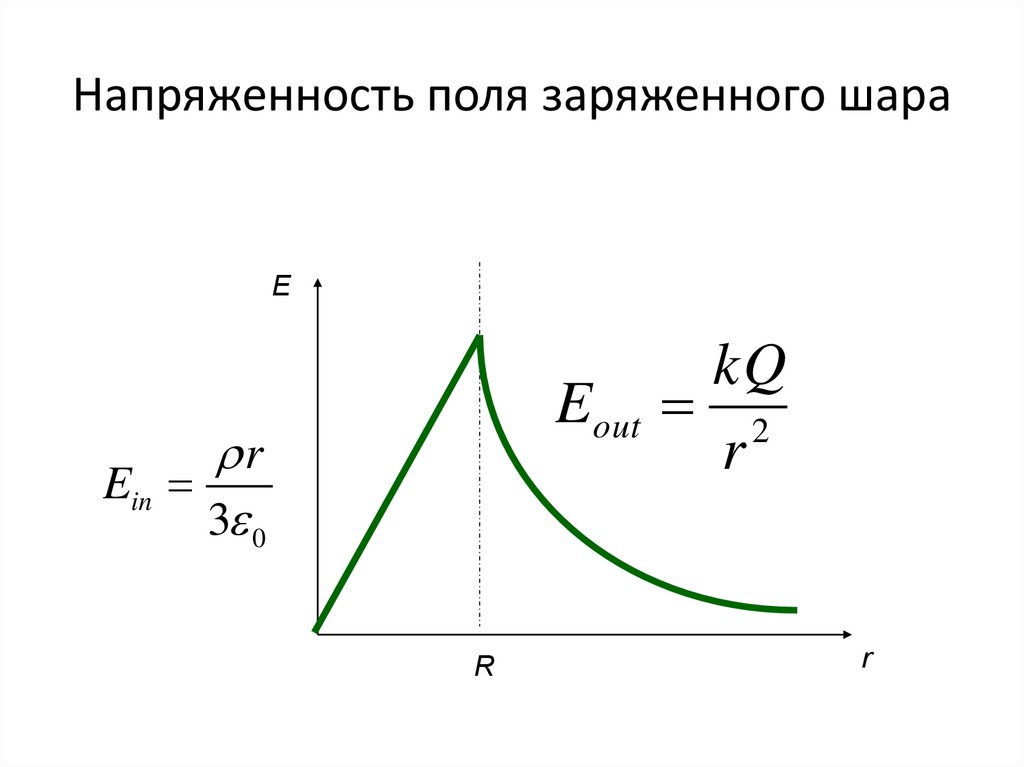
21. Напряженность поля заряженного шара
EEout
r
Ein
3 0
R
kQ
2
r
r
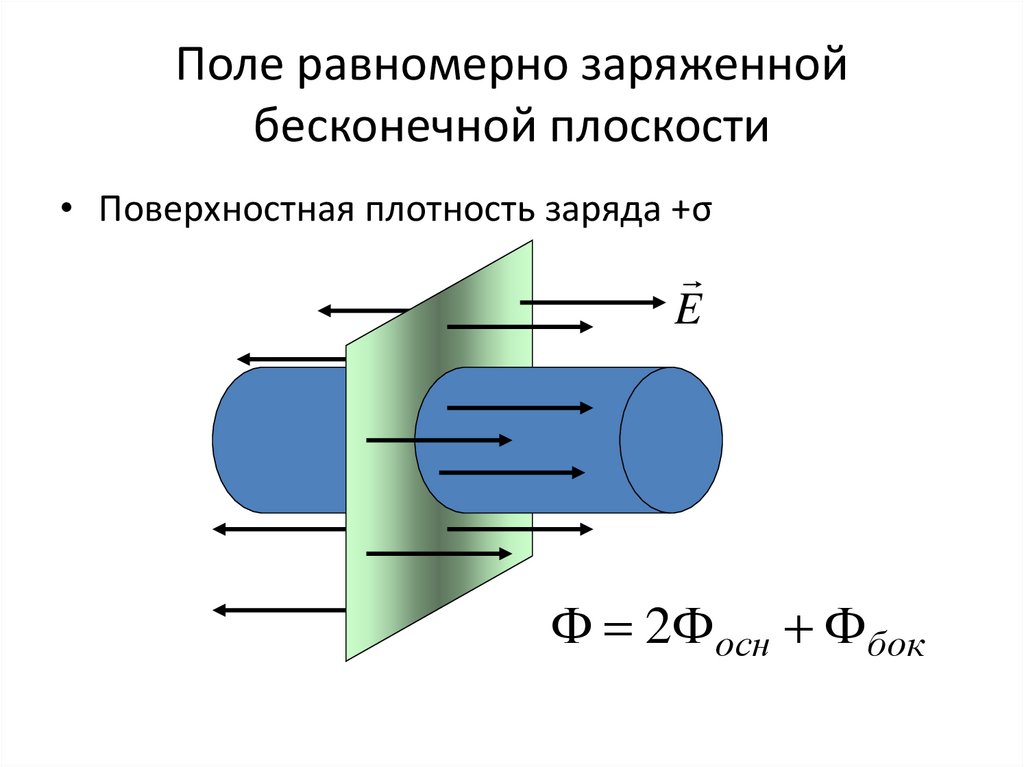
22. Поле равномерно заряженной бесконечной плоскости
• Поверхностная плотность заряда +σE
2 осн бок
23.
• Поток через боковую поверхность цилиндраdS
бок
s
E
E
dS
cos
E dS
2 0
S
24.
• Поток через основаниеr
осн
s
E
dS
E dS E dS cos0
E dS E r
S
S
2
25.
• Сумма зарядов внутри цилиндраQ
Q R
2
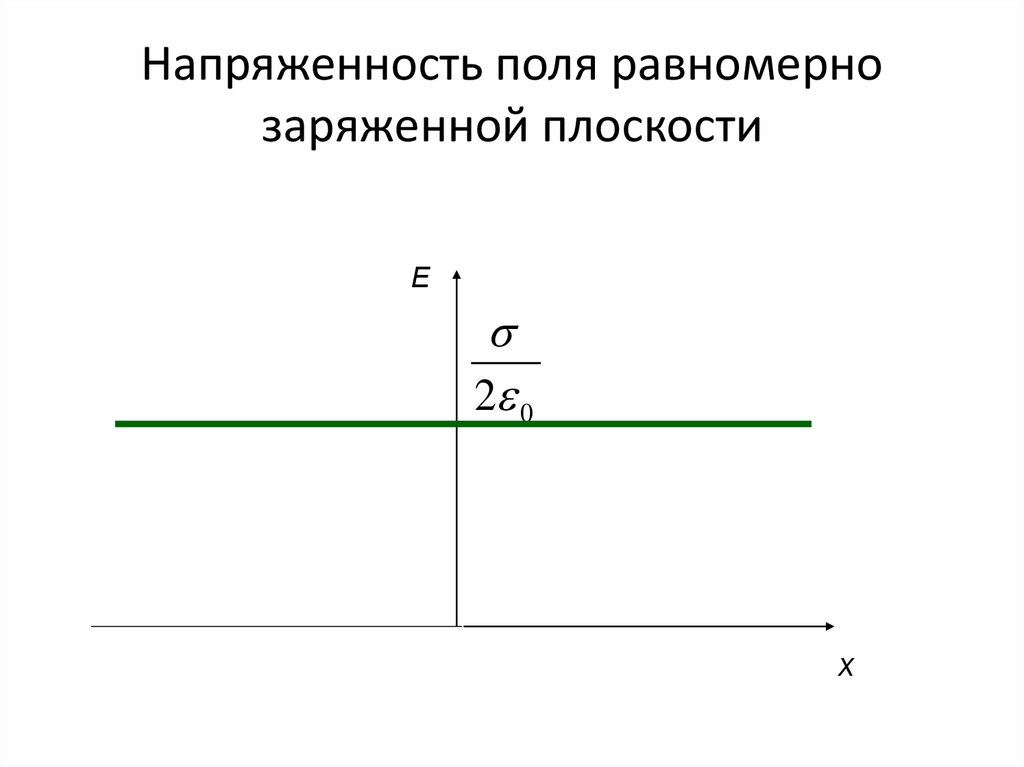
26. Напряженность равномерно заряженной плоскости
qiE dS
s
0
2 осн бок
r
2 E r
0
2
2 E r 0
2
2
E
2 0
27. Напряженность поля равномерно заряженной плоскости
E2 0
х
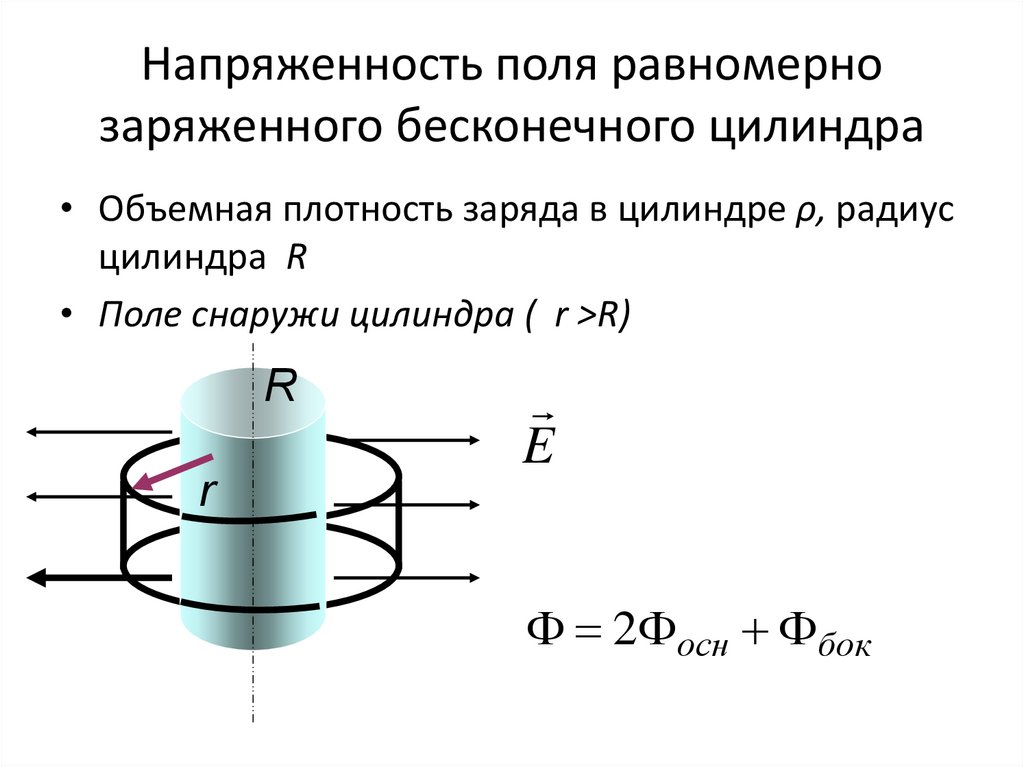
28. Напряженность поля равномерно заряженного бесконечного цилиндра
• Объемная плотность заряда в цилиндре ρ, радиусцилиндра R
• Поле снаружи цилиндра ( r >R)
R
r
E
2 осн бок
29. Поток через боковую поверхность цилиндра радиуса r
dSr
h
бок
s
E
E dS E dS cos0
S
E 2 rh
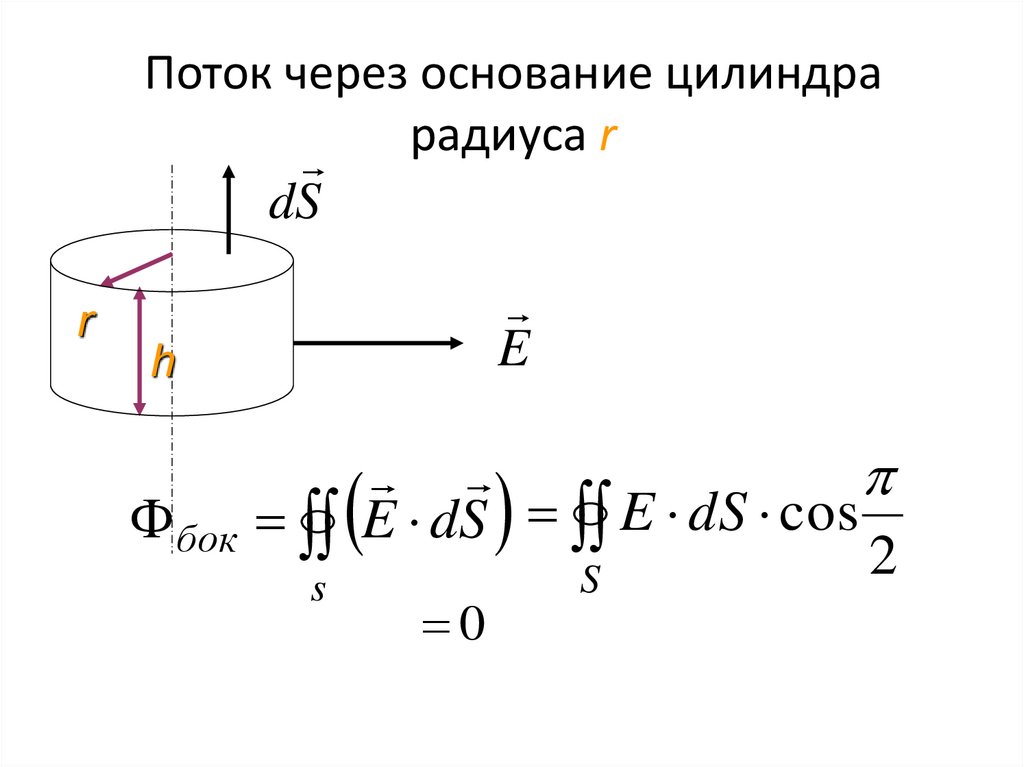
30. Поток через основание цилиндра радиуса r
dSr
E
h
бок
s
E dS E dS cos
2
S
0
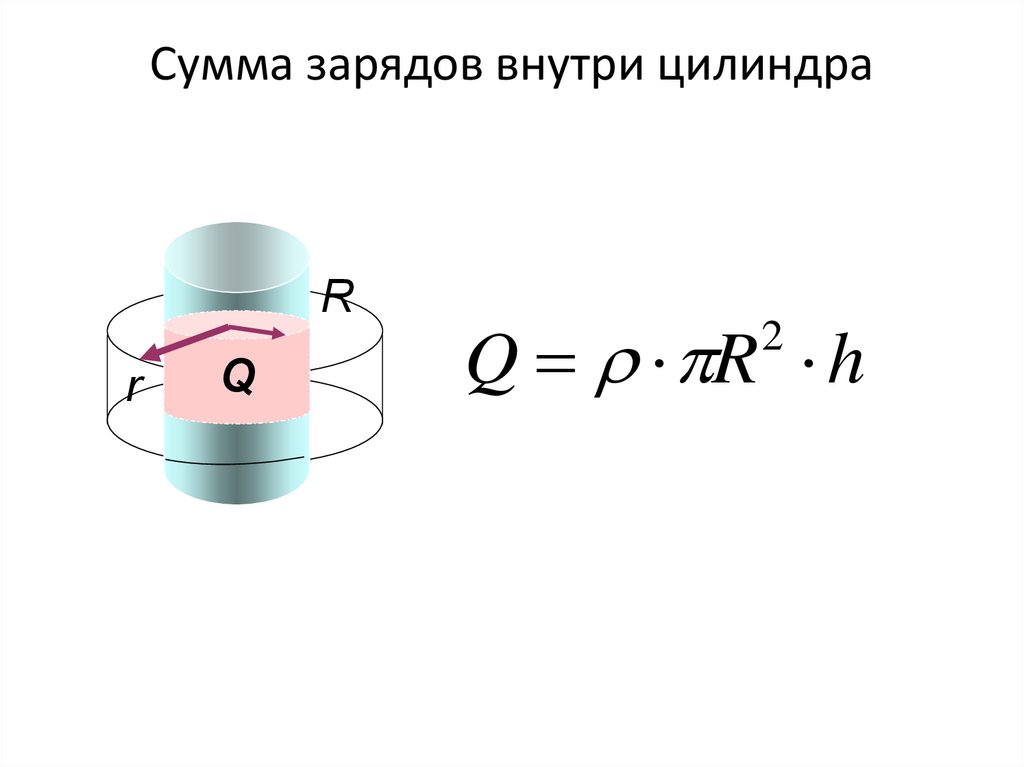
31. Сумма зарядов внутри цилиндра
Rr
Q
Q R h
2
32.
Напряженность равномернозаряженного бесконечного
цилиндра
qi
E dS
s
0
2 осн бок 0 E 2 rh
2
2
R h
R 1
E 2 rh
Eout
0
2 0 r
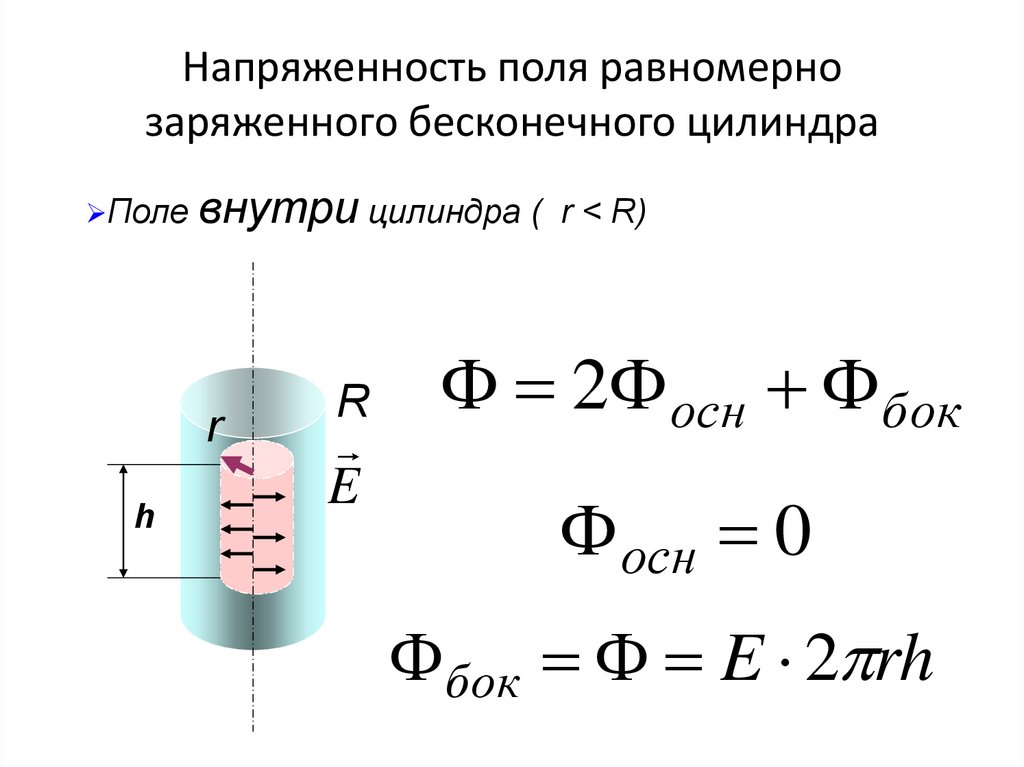
33. Напряженность поля равномерно заряженного бесконечного цилиндра
Полевнутри цилиндра (
r
h
R
E
r < R)
2 осн бок
осн 0
бок E 2 rh
34.
Сумма зарядов внутри цилиндраr
h
R
Q r h
2
35.
qiE dS
s
0
2 осн бок 0 E 2 rh
r h
E 2 rh
0
2
r
Ein
2 0
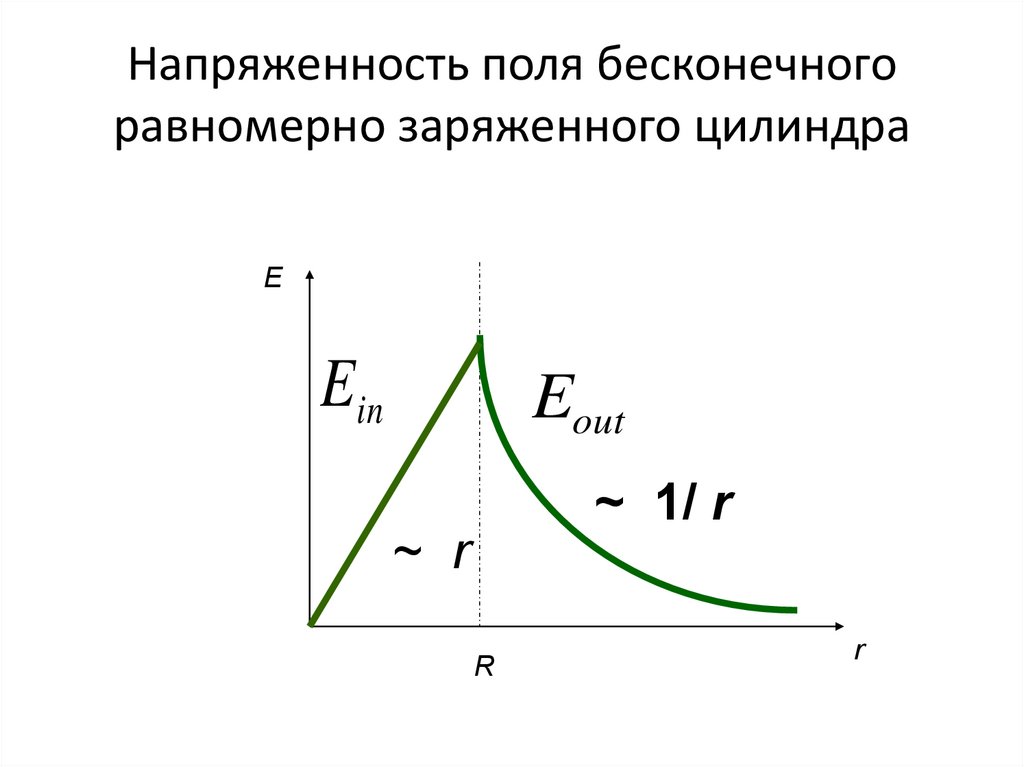
36. Напряженность поля бесконечного равномерно заряженного цилиндра
EEin
Eout
~ 1/ r
~ r
R
r
37.
Напряженность равномернозаряженного бесконечной нити
Линейная плотность заряда нити
r
E
38.
2 осн бок 0 E 2 rhh
E 2 rh
0
1
2 0 r
2
Eout
2k
r
39. Теорема Гаусса в дифференциальной форме
• Пусть заряд распределен в некоторойобласти пространства с плотностью ρ
Рассмотрим
поток вектора
напряженности через замкнутую
поверхность, когда ее объем
стремится к нулю
40.
1E dS ( x, y, z )dV
s
lim
V 0
0
V
1
E dS lim ( ( x, y, z )dV )
s
lim
V 0
V 0
0
V
E dS divE
s
Ex E y Ez
divE
x
y
z
дивергенция
41.
lim ( ( x, y, z )dV )V 0
0
0
V
1
divE
0
ТЕОРЕМА ГАУССА В
ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ
42.
• Дивергенция напряженности электрическогополя в данной точке зависит только от
локальной плотности заряда.
Там,
где div E положительна – имеем
положительные заряды – источники
поля
Там, где div E отрицательна – имеем
отрицательные заряды –стоки поля.
Линии
вектора напряженности идут от
истоков к стокам ( от положительных
зарядов к отрицательным)






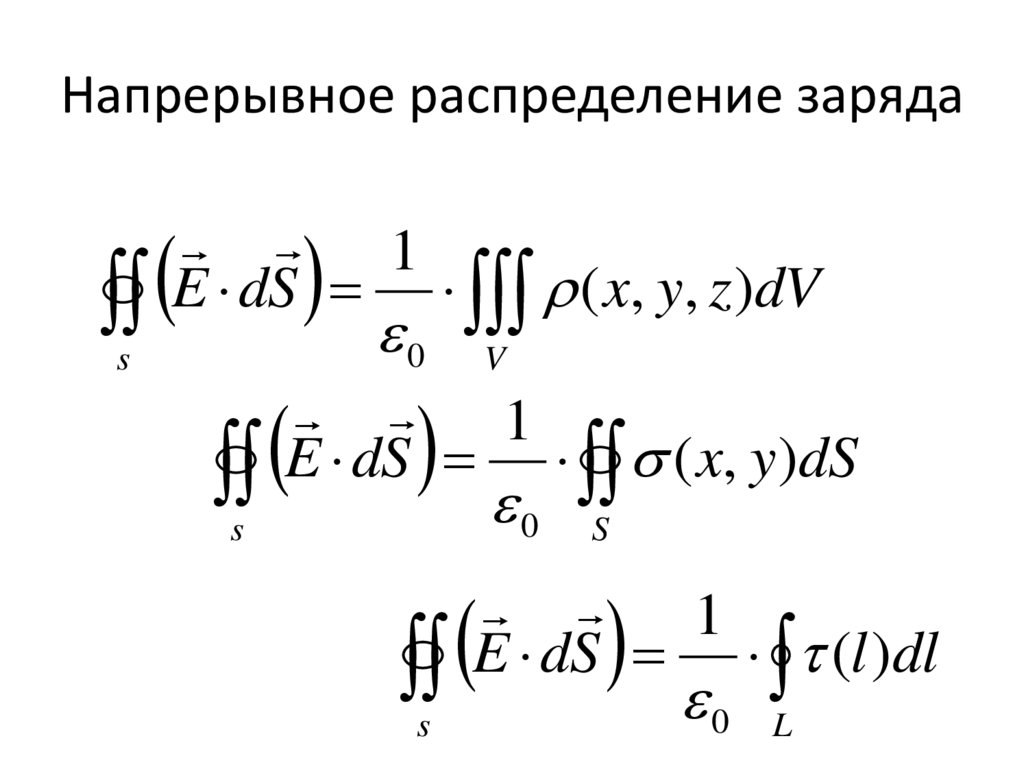



















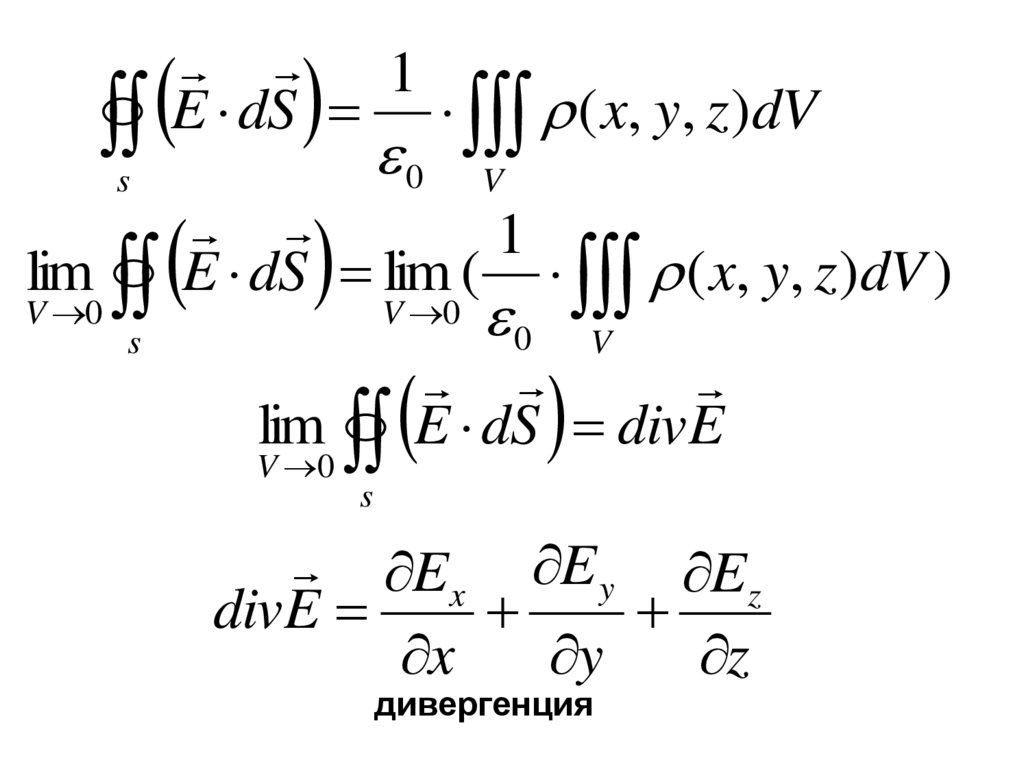



 Физика
Физика








