Обратная матрица. Лекция 3

1.

Матрица A-1 называется обратной к
матрице А, если
АA-1=A-1А=Е
где Е – единичная матрица

2.

1
Определяем, квадратная ли
матрица. Если нет, то
обратной матрицы для
нее не существует.

3.

2
Находим определитель матрицы.
Если он равен нулю, то обратной
матрицы не существует.

4.

3
Заменяем каждый элемент матрицы
его алгебраическим дополнением.

5.

4
Полученную матрицу транспонируем.

6.

5
Каждый элемент полученной
матрицы делим на определитель
исходной матрицы. Получаем
матрицу, обратную к данной.

7.

6
Делаем проверку. Для этого
перемножаем полученную и исходную
матрицы. Должна получиться
единичная матрица.

8.

Найти матрицу, обратную к матрице
2 1
A
3 2

9.

Применяем алгоритм нахождения обратной
матрицы.
1
Матрица
квадратная,
следовательно
обратная матрица для нее существует.
2
Находим определитель:
A
2 1
3 2
2 2 3 1 1 0

10.

3
Находим алгебраические дополнения
каждого элемента матрицы:
A11 ( 1) M11 2
2
A12 ( 1) M12 3
3
A21 ( 1)3 M 21 1
A22 ( 1) M 22 2
2
Составляем
матрицу:
из
полученных
2 3
1 2
значений

11.

4
Транспонируем ее:
T
2 3 2 1
1 2 3 2
5
Каждый элемент матрицы делим на
определитель Δ=1 и получаем обратную
матрицу:
2 1
A
3 2
1

12.

6
Проверяем:
2 1 2 1
A A
3 2 3 2
T
2 2 1 ( 3) 2 ( 1) 1 2 1 0
E
3 2 2 ( 3) 3 ( 1) 2 2 0 1

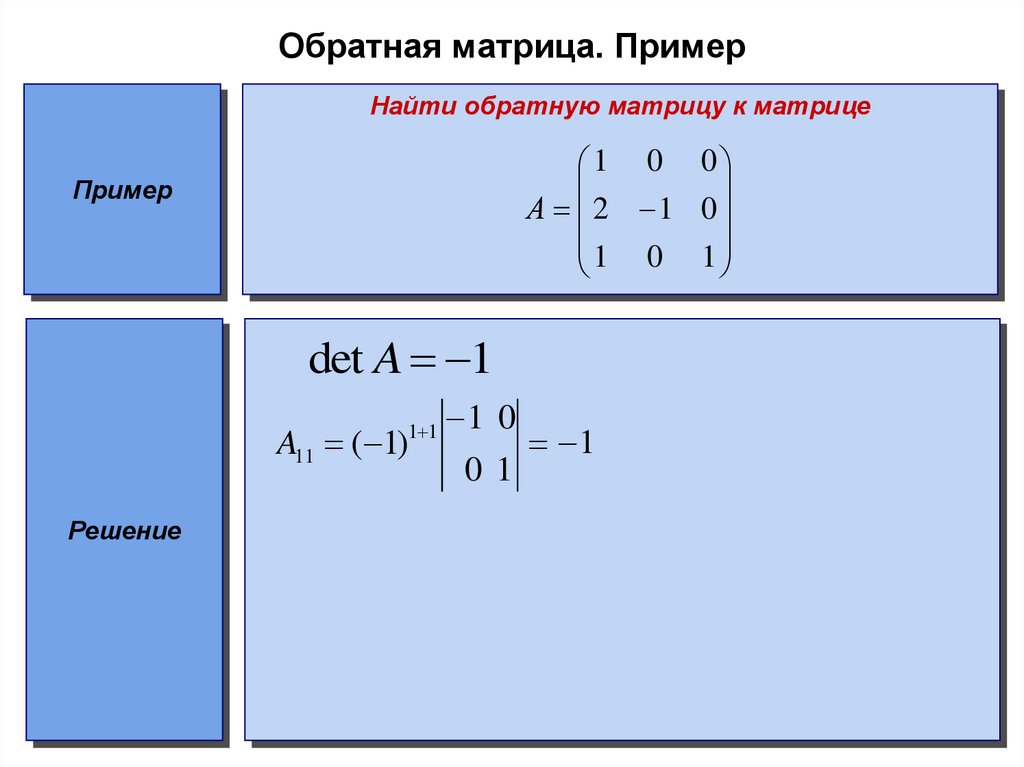
13. Обратная матрица. Пример

Найти обратную матрицу к матрице
Пример
1 0 0
А 2 1 0
1 0 1

14. Обратная матрица. Пример

Найти обратную матрицу к матрице
1 0 0
А 2 1 0
1 0 1
Пример
det A 1
Решение

15. Обратная матрица. Пример

Найти обратную матрицу к матрице
1 0 0
А 2 1 0
1 0 1
Пример
det A 1
1 1
A11 ( 1)
Решение
1 0
01
1

16. Обратная матрица. Пример

Найти обратную матрицу к матрице
1 0 0
А 2 1 0
1 0 1
Пример
det A 1
1 1
A11 ( 1)
Решение
1 0
01
1

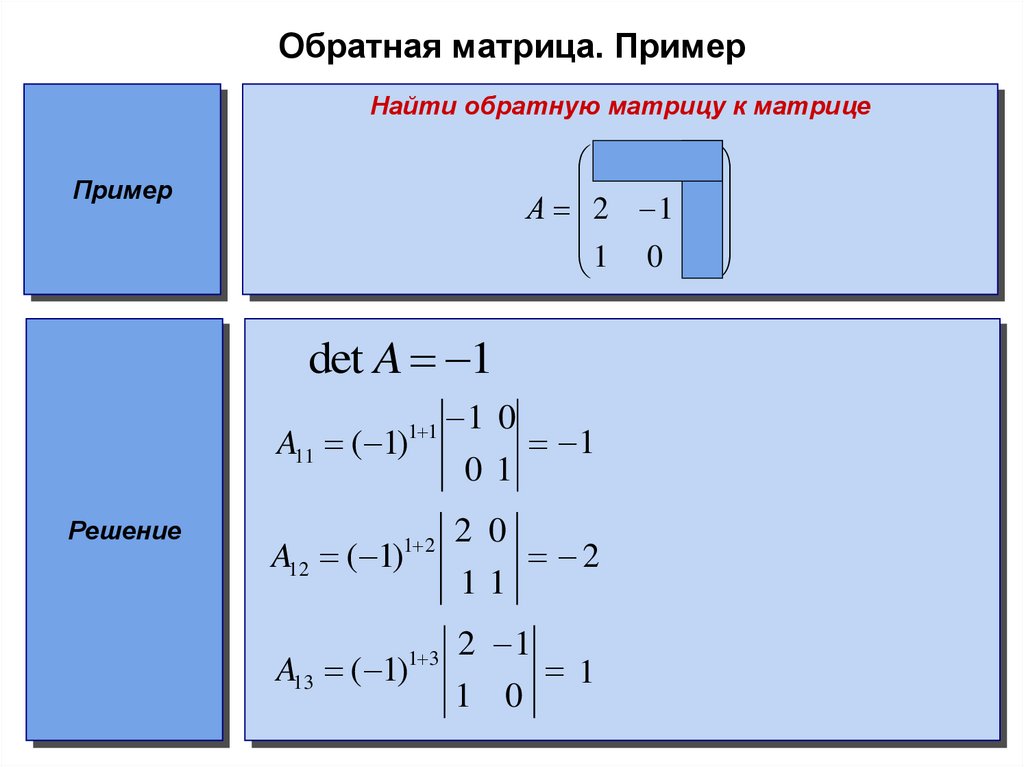
17. Обратная матрица. Пример

Найти обратную матрицу к матрице
1 0 0
А 2 1 0
1 0 1
Пример
det A 1
1 1
A11 ( 1)
Решение
1 2
A12 ( 1)
1 0
01
2 0
11
1
2

18. Обратная матрица. Пример

Найти обратную матрицу к матрице
1 0 0
А 2 1 0
1 0 1
Пример
det A 1
1 1
A11 ( 1)
Решение
1 2
A12 ( 1)
1 0
01
2 0
11
1 3
A13 ( 1)
1
2
2 1
1 0
1

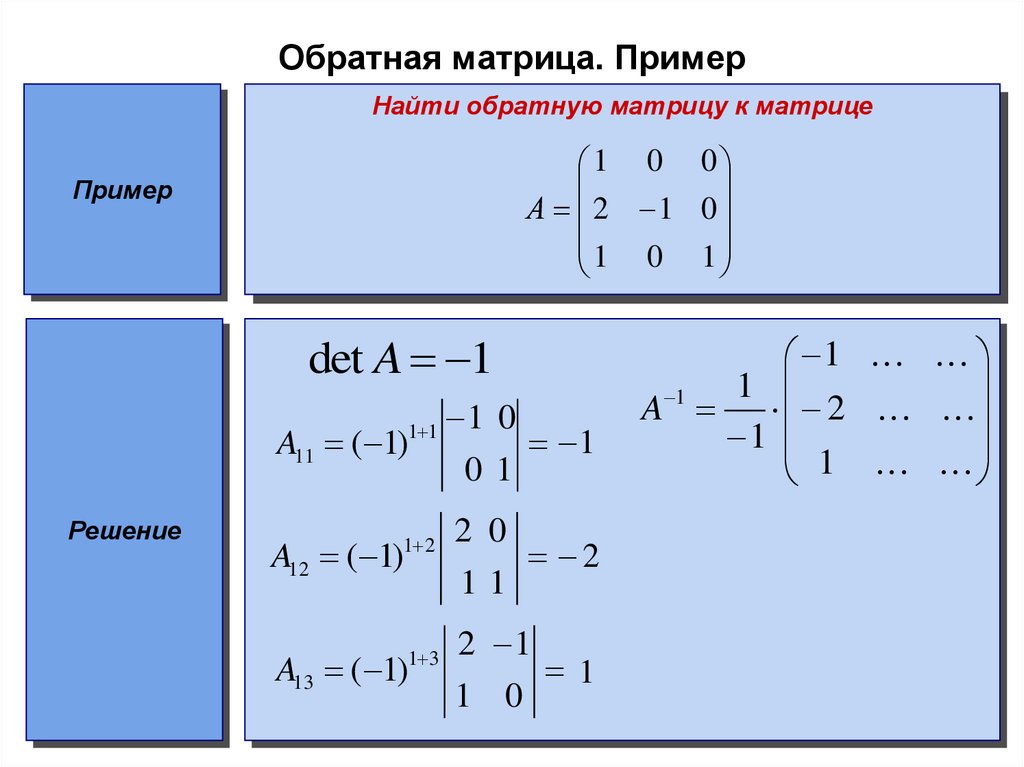
19. Обратная матрица. Пример

Найти обратную матрицу к матрице
1 0 0
А 2 1 0
1 0 1
Пример
det A 1
1 1
A11 ( 1)
Решение
1 2
A12 ( 1)
1 0
01
2 0
11
1 3
A13 ( 1)
1
2
2 1
1 0
1
1
1
1
A
2
1
1

20. Обратная матрица. Пример

1
1
1
A 2
1
1
1 0 0
А 2 1 0
1 0 1
A21 ( 1)
2 1
0 0
01
0

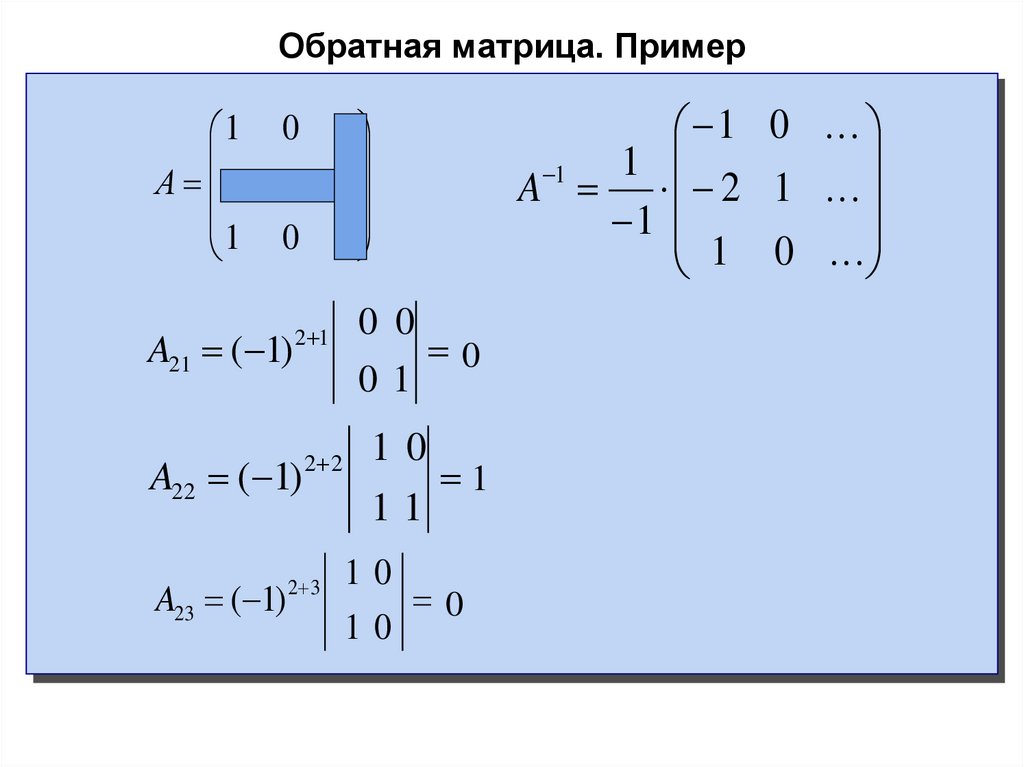
21. Обратная матрица. Пример

1
1
1
A 2
1
1
1 0 0
А 2 1 0
1 0 1
A21 ( 1)
2 1
A22 ( 1)
0 0
01
2 2
10
11
0
1

22. Обратная матрица. Пример

1 0
1
1
A 2 1
1
1
0
1 0 0
А 2 1 0
1 0 1
A21 ( 1)
2 1
A22 ( 1)
A23 ( 1)
0 0
01
2 2
2 3
10
11
10
10
0
1
0

23. Обратная матрица. Пример

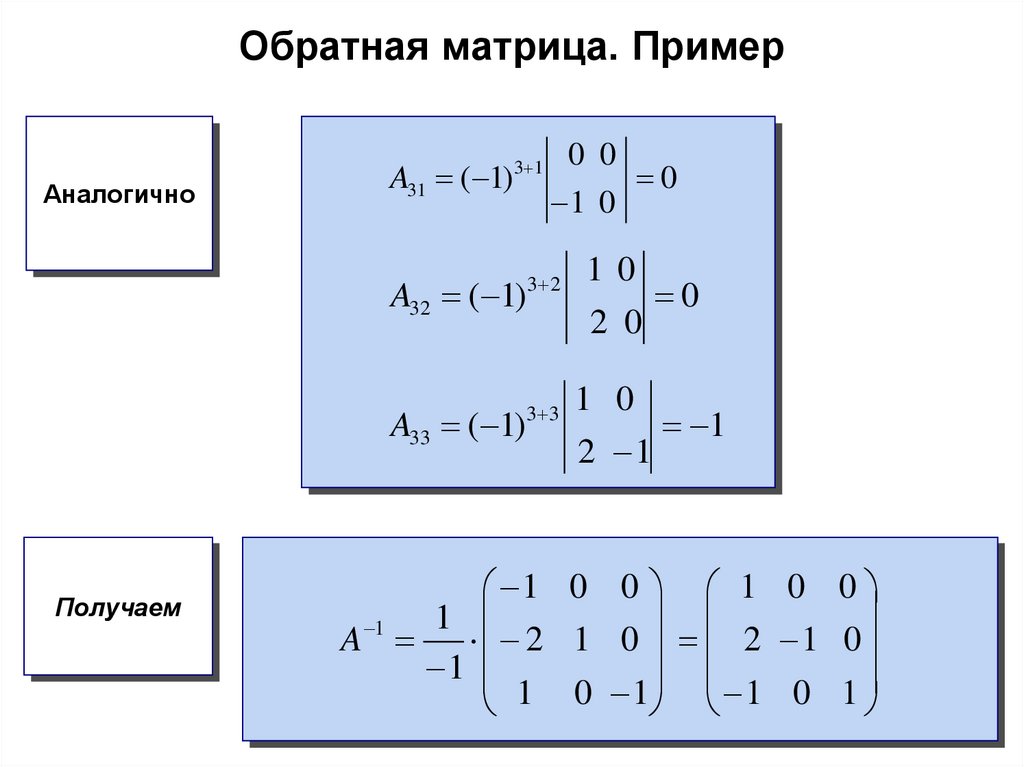
Аналогично
Получаем
A31 ( 1)
0 0
3 1
1 0
A32 ( 1)
3 2
A33 ( 1)
3 3
0
1 0
2 0
1 0
2 1
0
1
1 0 0 1 0 0
1
1
A
2 1 0 2 1 0
1
1 0 1
1
0
1