Похожие презентации:
Скалярное произведение векторов. Вычисление углов между прямыми
1.
Скалярное произведениевекторов.
Вычисление углов между
прямыми.
2.
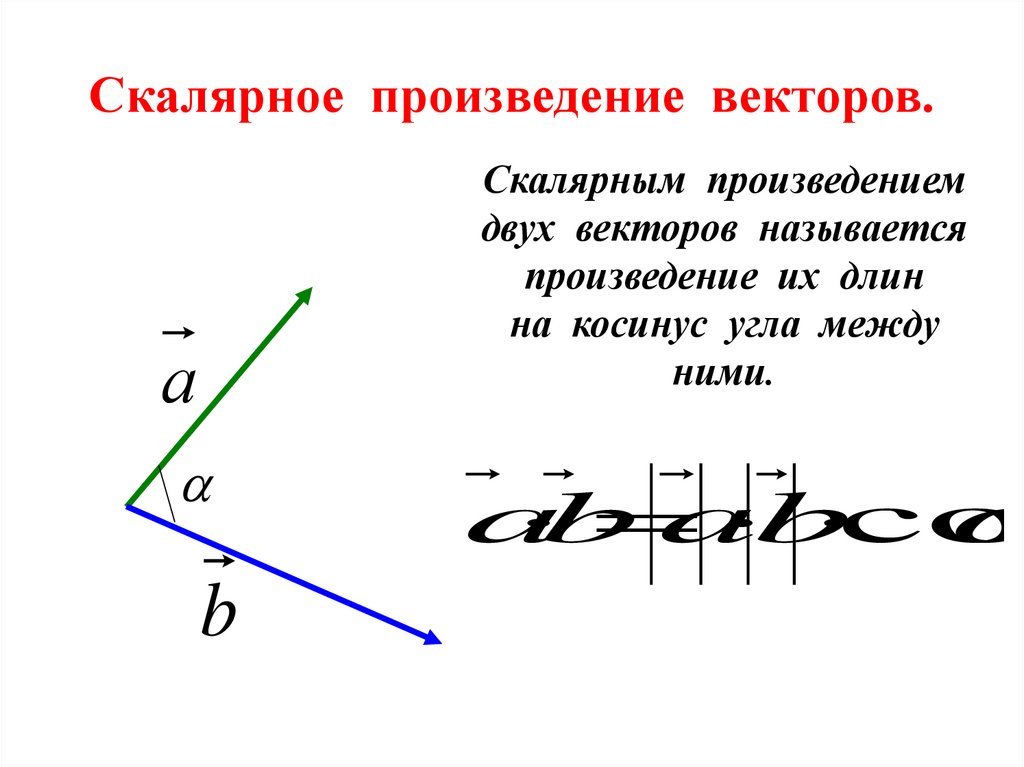
Скалярное произведение векторов.Скалярным произведением
двух векторов называется
произведение их длин
на косинус угла между
ними.
а
b
a
b
a
b
cos
3.
Свойства скалярного произведения векторовДля любых векторов
a, b, cи любого числа k справедливы равенства:
1
a 2 0 причем
2
a b = b a
3
(a + b) c = a c + b c
a 2 при
>0
a 0
Переместительный закон
Распределительный закон
4
(ka) b = k(a b)
Сочетательный закон
4. Скаляр – лат. scale – шкала.
Ввел в 1845 г.У. ГАМИЛЬТОН,
английский
математик.
5.
ab a b cos
Если
Если
Если
a b = 0
a b 0
, то
a b
- острый угол
a b 0 , то - тупой угол
, то
6. Формула скалярного произведения векторов в пространстве.
а x1 ; y1 ; z1b x2 ; y2 ; z2
a b x1 x2 y1 y2 z1 z2
Скалярное произведение двух векторов равно
сумме произведений соответствующих
координат этих векторов.
7.
a {3; -4; 2}, b {-2; 1; 3}, c {-2;-1,5; 0}Каким (острым, тупым или прямым) является угол между
Найдите
векторами
и ,
и ,
и
a
b bc
c a
a b = 3 (-2) + (-4) 1 + 2 3 = - 4
b c = (-2) (-2) + 1 (- 1,5) + 3 0 = 2,5
c a = 3 (-2) + (-4) (- 1,5) + 2 0 = 0
тупой
острый
прямой
8.
a {1; -1; 2}, b {-1; 1; 1}, c {5; 6; 2}Вычислить
a c = 1 5 + (-1) 6 + 2 2 = 3
a b = 1 (-1) + (-1) 1 + 2 1 = 0
b c = -1 5 + 1 6 + 1 2 = 3
a a = 1 1 + (-1) (-1) + 2 2 = 6
b b = -1 (-1) + 1 1 + 1 1 =
3
9.
Формула скалярного произведениявекторов в пространстве.
а x1;y1;z1
b x2;y2;z2
a
b
x
x
y
y
z
z
1
2
1
2
1
2
Косинус угла между ненулевыми
векторами
x
x
y
y
z
z
1
2
1
2
1
2
cos
2 2 2
2 2 2
x
y
z
x
y
z
1
1
1
2
2
2
10.
ЗадачаAB 1;0; 1
Вычислить угол между векторами СD 0; 2;2
Решение
AB 1;0; 1
cos =
x
x
y
y
z
z
1
2
1
2
1
2
cos
2 2 2
2 2 2
x
y
z
x
y
z
1 1 1
2
2
2
СD 0; 2;2
| 1 0 0 ( 2) ( 1) 2 |
12 0 2 ( 1) 2 0 2 ( 2) 2 2 2
1
cos
2
60
0
11.
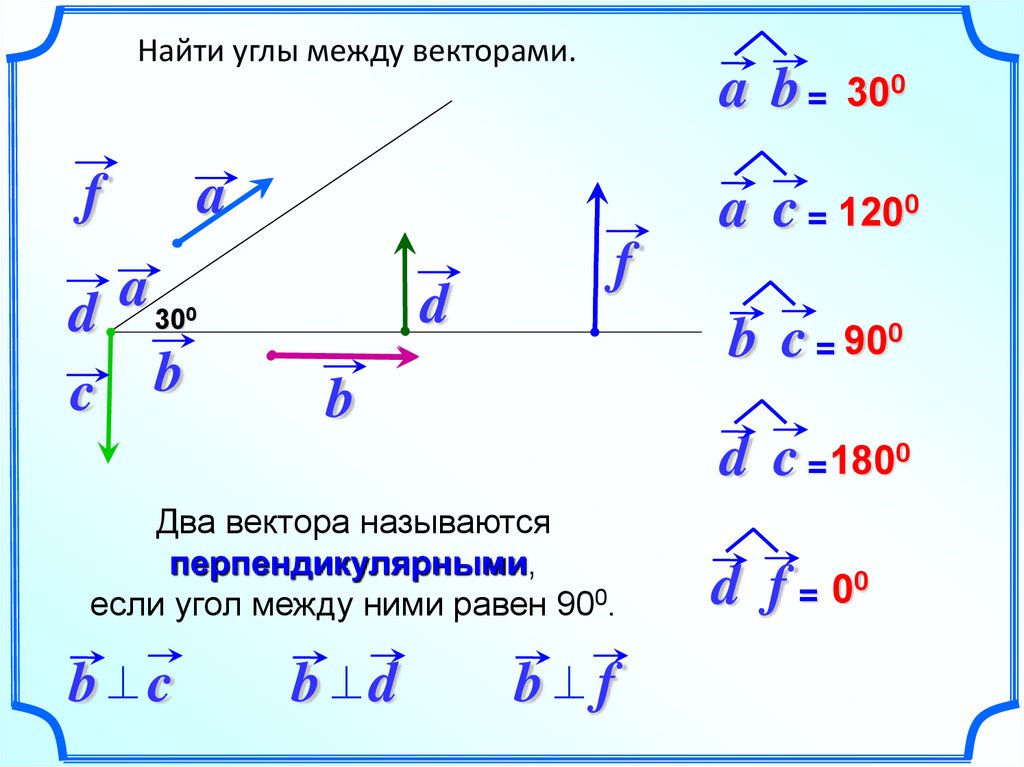
Найти углы между векторами.f
a
a
d 30
c
a b = 300
b
a c = 1200
d
0
f
b c = 900
b
d c = 1800
Два вектора называются
перпендикулярными,
если угол между ними равен 900.
b c
b d
b f
d f = 00
12.
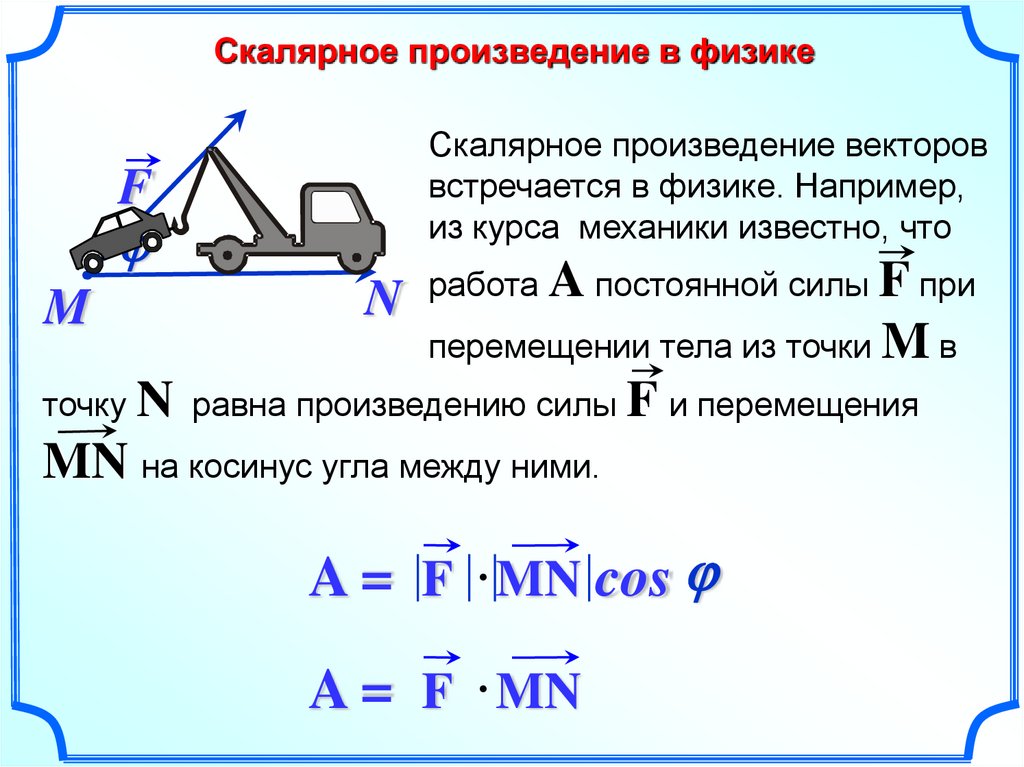
Скалярное произведение в физикеF
Скалярное произведение векторов
встречается в физике. Например,
из курса механики известно, что
работа A постоянной силы F при
N
M
перемещении тела из точки M в
точку N равна произведению силы F и перемещения
MN на косинус угла между ними.
A = F MN cos
A = F MN
13.
a b = 900b
a b = a b cos 900 = 0
a
a
b
Если векторы
и
перпендикулярны, то скалярное
произведение векторов равно нулю.
a b ,=то0 векторы
Обратно: если
перпендикулярны.
и
a
b
Скалярное произведение ненулевых векторов равно
нулю тогда и только тогда, когда эти векторы
перпендикулярны.
a b =0
a b
14.
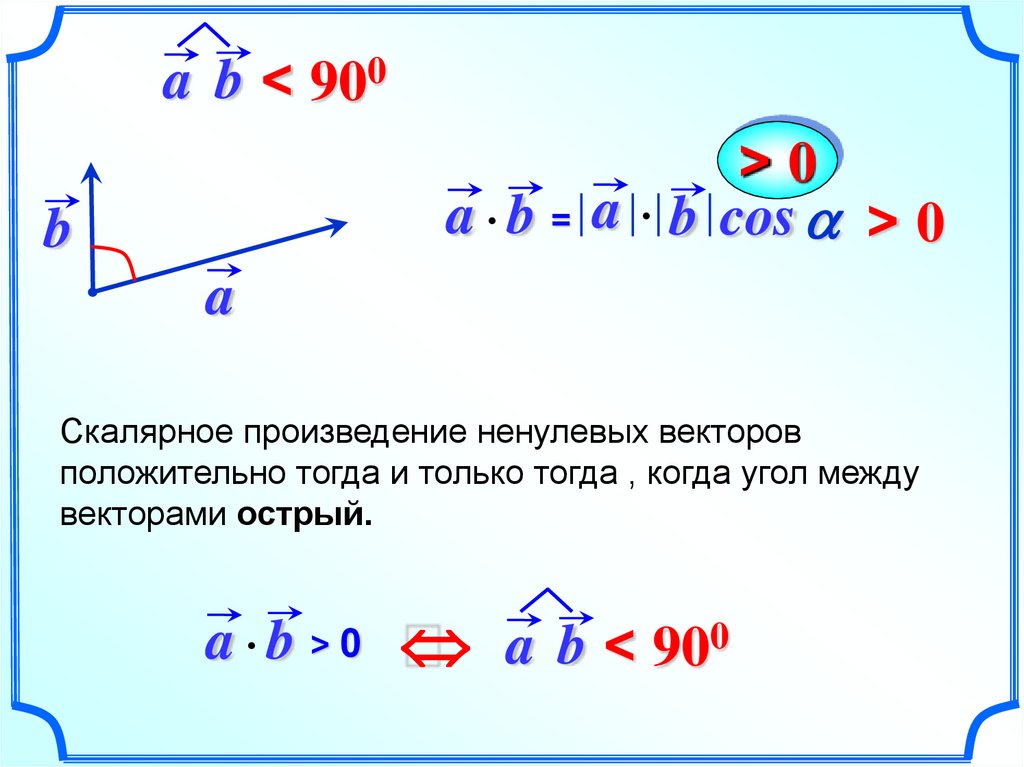
a b < 900>0
a b = a b cos > 0
b
a
Скалярное произведение ненулевых векторов
положительно тогда и только тогда , когда угол между
векторами острый.
a b > 0 a b < 900
15.
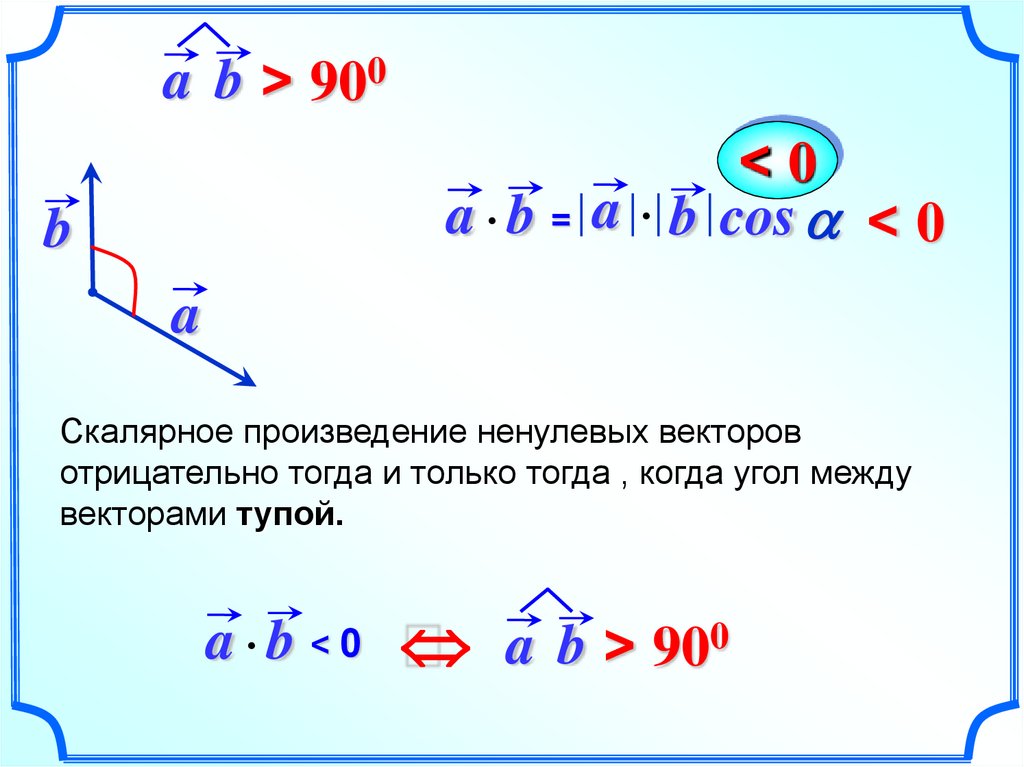
a b > 900<0
a b = a b cos < 0
b
a
Скалярное произведение ненулевых векторов
отрицательно тогда и только тогда , когда угол между
векторами тупой.
a b < 0 a b > 900
16.
Угол между прямымир - направляющий вектор прямой а
а
р
q - направляющий вектор прямой b
- угол между прямыми
q
b
p x1 ; y1 ; z1
р
q
cos =
q x2 ; y2 ; z2
| x1 x2 + y1 y2 + z1 z 2 |
x +y +z x +y +z
2
1
2
1
2
1
2
2
2
2
2
2



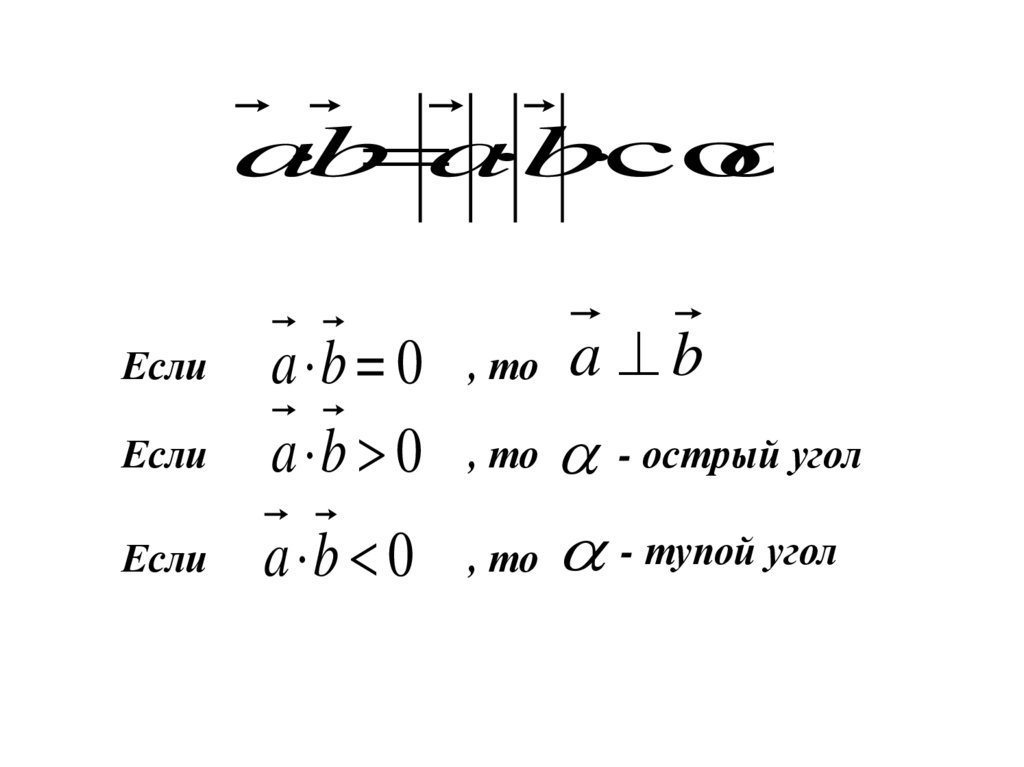







 Математика
Математика








