Похожие презентации:
Методическая разработка урока геометрии «Основные формулы метода координат в пространстве». Урок №1
1.
Методическая разработка урока геометрии«Основные формулы метода координат в
пространстве»
Урок №1
2.
Цели:• Изучить основные формулы метода координат
в пространстве
• Рассмотреть методику использования данных
формул при решении задач
• Применить изученный материал при решении
задач методом координат
07.02.2022
2
3.
Повторяем теорию:• Как находят координаты вектора, если известны координаты
его начала и конца?
АВ х В х А ; у В у А ; z B z A
• Как находят координаты середины отрезка?
х А хВ
;
2
• Как находят длину вектора?
у А уВ
;
2
z A zB
2
а х2 у2 z 2
• Как находят расстояние между точками?
АВ
х
х А у В у А z B z A
2
В
2
2
4.
Повторяем теорию:• Какие векторы называются перпендикулярными?
• Что называется скалярным произведением векторов?
а b a b cos
• Чему равно скалярное произведение
перпендикулярных векторов?
0
• Чему равен скалярный квадрат вектора?
Скалярный квадрат вектора равен квадрату его длины.
5.
Введение• В стереометрии используется два основных метода решения задач.
Первый метод основан на аксиомах, теоремах и свойствах фигур. Он
требует логической последовательности практических рассуждений.
Второй метод – это метод координат или координатно-векторный метод,
его можно успешно применять при решении большого числа задач, в том
числе, задач Единого Государственного экзамена (задания С2 или № 17 ).
А так как, эти задания - повышенной сложности, то они приносят
учащимся хорошие баллы при сдаче ЕГЭ.
• Сущность метода координат как метода решения задач состоит в том, что,
задавая фигуры уравнениями и выражая в координатах различные
геометрические соотношения, мы можем решать геометрическую задачу
средствами алгебры.
• В отношении школьного курса геометрии можно сказать, что в некоторых
случаях метод координат дает возможность строить доказательства и
решать многие задачи более рационально, красиво, чем чисто
геометрическими способами.
07.02.2022
5
6.
Этапы решения задач методомкоординат
• 1. Выбор системы координат в пространстве
• 2. Нахождение координат необходимых точек и
векторов, или уравнения плоскостей, кривых и
фигур
• 3. Решение примера, используя ключевые задачи
или формулы данного метода
• 4. Переход от аналитических соотношений к
метрическим.
07.02.2022
6
7.
Угол между прямыми а и в07.02.2022
7
8.
Вектор нормали к плоскостиN
M
P
– вектор нормали плоскости
– это вектор перпендикулярный
этой плоскости
Уравнение плоскости:
где A, B, C – координаты вектора нормали плоскости,
9.
Угол между прямой и плоскостью07.02.2022
9
10.
Угол между плоскостями07.02.2022
10
11.
Расстояния в пространстве• Расстояние между двумя точками А и В
Расстояние от точки А до плоскости
07.02.2022
11
12.
Расстояние от точки М до прямой а07.02.2022
12
13.
Расстояние между скрещивающимисяпрямыми а и в
07.02.2022
13
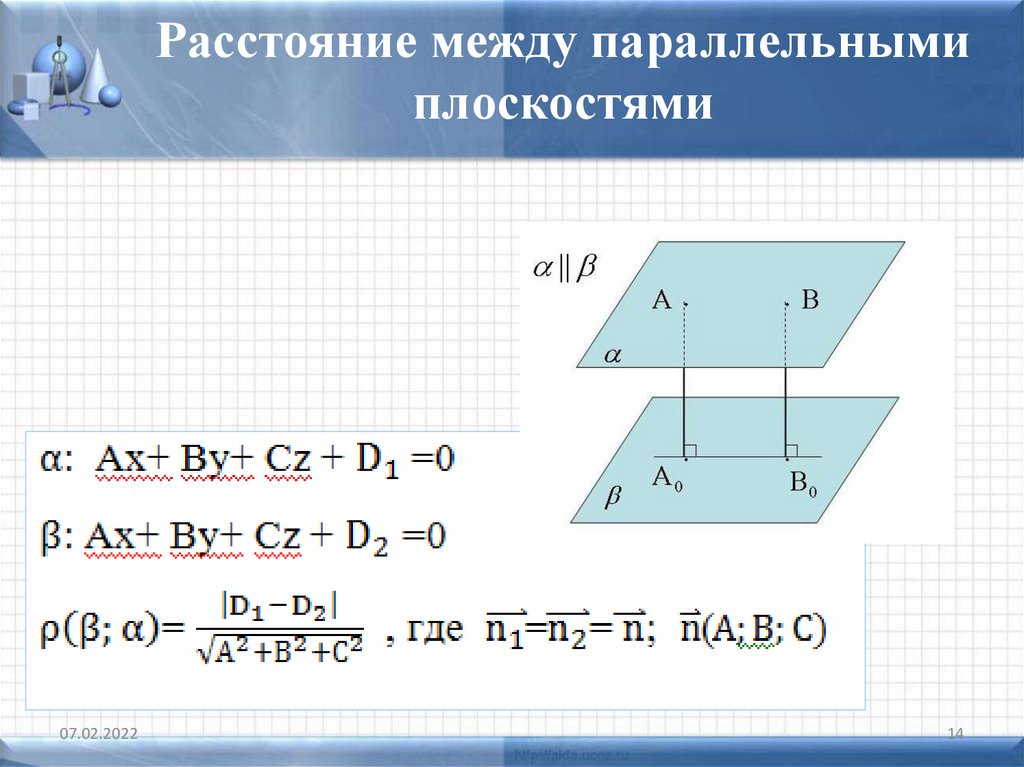
14.
Расстояние между параллельнымиплоскостями
07.02.2022
14
15.
№1Дано: А 3; 2;4 В 4; 1;2 С 6; 3;2 D 7; 3;1
Найти: угол между прямыми АВ и CD.
Ваши предложения…
1. Найдем координаты векторов
АВ 1;1; 2 и CD 1;0; 1
2. Воспользуемся формулой:
cos
x1 x2 y1 y 2 z1 z 2
x y z x y z
2
1
2
1
2
1
2
2
2
2
2
2
φ = 300
16.
№2Дано: куб АВСDA1B1C1D1 , точка М принадлежит
АА1; АМ : МА1 = 3 : 1; N – середина ВС
Вычислить косинус угла между прям. MN и DD1
z
1. Введем систему координат.
2. Рассмотрим DD1 и МN.
3. Пусть АА1= 4, тогда
D1
1
A1
М 0;4;3 N 4;2;0
4. Найдем координаты векторов М
DD1 и MN.
5. По формуле найдем cosφ.
Ответ:
3
29
C
A
у
B1
D
C
B
N
х















 Математика
Математика








