Похожие презентации:
Решение логарифмических неравенств
1.
Решение логарифмическихнеравенств
2.
Логарифмическим неравенствомназывается неравенство, в котором
переменная находится под знаком
логарифма
Логарифмическими неравенствами
называют неравенства вида
3.
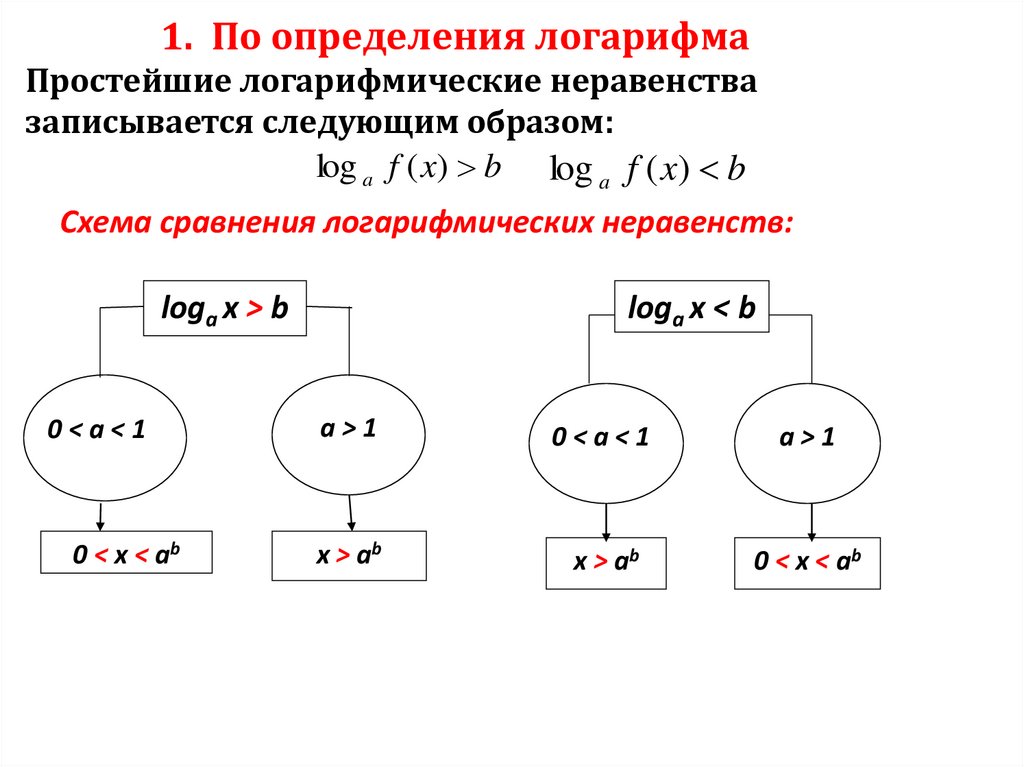
1. По определения логарифмаПростейшие логарифмические неравенства
записывается следующим образом:
log a f ( x) b log a f ( x) b
Схема сравнения логарифмических неравенств:
logа x > b
0<a<1
0 < x < ab
logа x < b
a>1
0<a<1
a>1
x > ab
x > ab
0 < x < ab
4.
Ответ : (3; )+
-1
+
4
1
1
-
2
2
+
х
+
Ответ : [ 1;1) (2;4].
х
5.
2. Метод потенцированияСуть метода в следующем: с помощью формул
неравенство привести к виду log a f ( x) log a g ( x)
Справедливы следующие утверждения:
f ( x) g ( x),
log a f ( x) log a g ( x) f ( x) 0, a 1
g ( x) 0;
f ( x) g ( x),
log a f ( x) log a g ( x) f ( x) 0, 0 a 1
g ( x) 0;
6.
1) log 5 (2 x) log 5 ( x 1)Т .к. 5 1, то функция у log 5 t возрастающая
и, учитывая ОДЗ , получаем
2 х х 1
х 1
х 1
х 1 0
х 1
Ответ : (1; )
7.
2) log 1 (2 x) log 1 ( x 1)2
2
1
Т .к. 0 1, то функция у log 1 t убывающая
2
2
и, учитывая ОДЗ , получаем
2 х х 1
х 1
решений нет
2 х 0
х 0
Ответ : решений нет
8.
3).9.
Самостоятельно :1) log 1 ( x 2) log 1 4 х
3
3
10.
Найдите ошибку:log8 (5х-10) < log8(14-х),
5x-10 < 14-x,
6x < 24,
x < 4.
Ответ: х (-∞; 4).
Решить верно:
log8 (5х-10)< log8(14-х)
Ответ: х (2;4).
11.
3.Метод введения новой переменной:Ищем в неравенстве некоторое повторяющееся
выражение,
которое
обозначим
новой
переменной,
тем
самым,
упрощая
вид
неравенства. Например:
12.
13.
Физминутка для глаз14.
Правильному применению методовможно научиться, только применяя их на
различных примерах
Цейтен






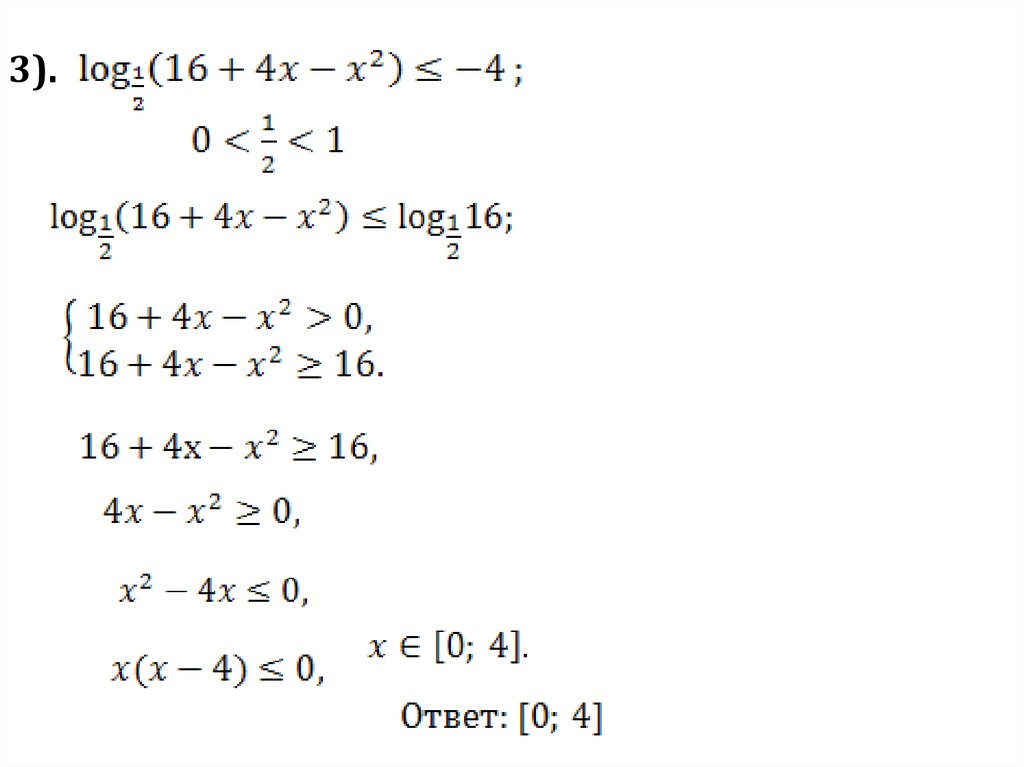







 Математика
Математика








