Похожие презентации:
Решение логарифмических уравнений и неравенств
1.
Решениелогарифмических
уравнений и неравенств.
2.
Логарифмические уравненияУравнения, содержащие неизвестное
под знаком логарифма или в основании
логарифма называются
логарифмическими.
log a f ( x) b
log f ( x ) b a
3.
Решение уравнений, содержащихнеизвестное под знаком логарифма,
основано на следующих теоремах:
log a f ( x) g ( x)
log a ( f ( x)) 2 n g ( x)
f ( x) a
2n log a f ( x) g ( x)
g ( x)
log a f ( x) log a g ( x)
f ( x) g ( x)
f ( x) 0
g ( x) 0
4.
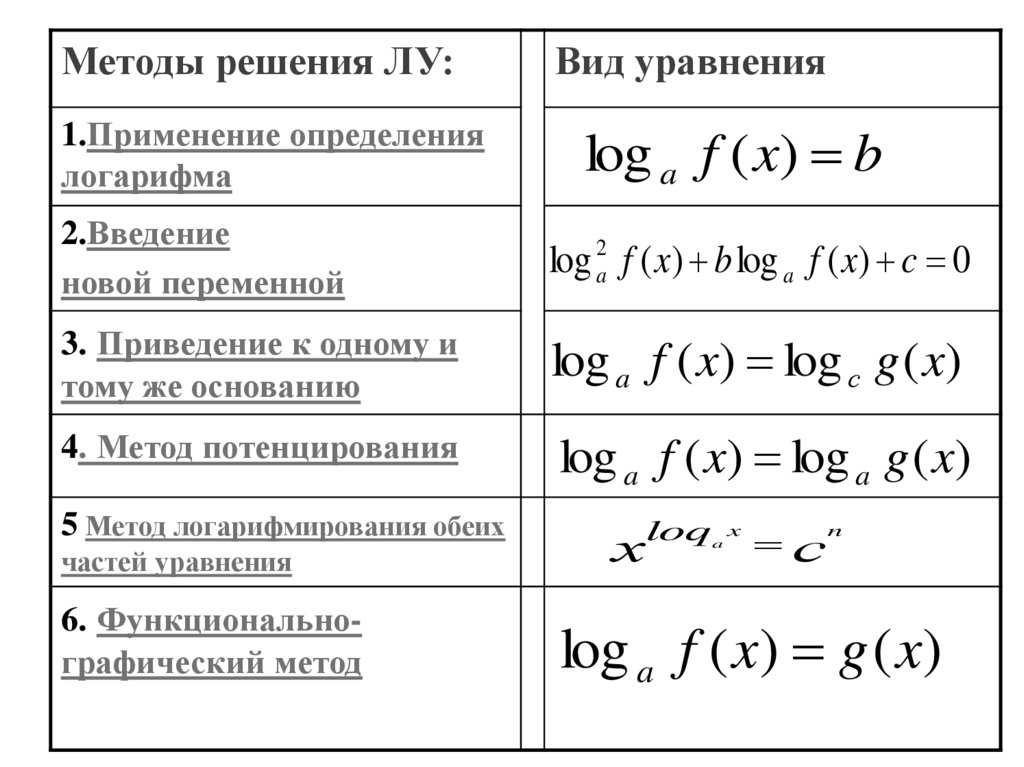
Методы решения ЛУ:1.Применение определения
логарифма
Вид уравнения
log a f ( x) b
2.Введение
новой переменной
log f ( x) b log a f ( x) c 0
3. Приведение к одному и
тому же основанию
log a f ( x) log с g ( x)
4. Метод потенцирования
log a f ( x) log a g ( x)
5 Метод логарифмирования обеих
частей уравнения
6. Функциональнографический метод
2
a
loq a x
х
с
n
log a f ( x) g ( x)
5.
Метод замены переменной:3 log 2 x 7 log 2 x 2 0
2
log 0, 2 x log 0, 2 x 6 0
2
1
2
1
4 lg x 2 lg x
Признак: Все логарифмы
в уравнении могут быть
сведены к одному и тому же
логарифму, содержащему
переменную.
1. Определить ОДЗ уравнения
(подлогарифмические
выражения положительны);
2. Произвести замену
переменной;
3. Решить полученное
уравнение;
4. Составить простейшие
логарифмические уравнения,
возвращаясь к
первоначальной
переменной;
5. Проверить полученные корни
по ОДЗ;
6. Записать удовлетворяющие
ОДЗ корни в ответ.
6.
log a f x log a g xМетод потенциирования:
log 1 7 x 9 log 1 x;
log 23 2 x 1 log 23 x
6
6
log 23 x 2
lg x 8 lg 2 9 x
2
Признак: уравнение может
быть представлено в виде
равенства двух логарифмов
по одному основанию .
1. Определить ОДЗ уравнения
(подлогарифмические
выражения положительны);
2. Пропотенцировать обе части
уравнения по основанию
равному основанию
логарифма;
3. Перейти к равенству
подлогарифмических
выражений, применив
свойство логарифма;
4. Решить уравнение и проверить
полученные корни по ОДЗ;
5. Записать удовлетворяющие
ОДЗ корни в ответ.
7.
Метод логарифмирования:x
10
2 log 3 x
x
9
lg x
2x
log 2 x
1.
2.
32
Признак: переменная
содержится и в основании
степени, и в показателе
степени под знаком
логарифма.
3.
4.
Определить ОДЗ
уравнения
(подлогарифмические
выражения
положительны);
Прологарифмировать обе
части уравнения по
основанию равному
основанию логарифма в
показателе степени;
Вынести показатель
степени за знак
логарифма, пользуясь
свойством логарифма;
Решить полученное
уравнение, пользуясь
методом замены
переменной.
8.
Выбери метод решения уравнения1
1) log 3 (4 x 1) 2 log 1
x 1
3
2) log
1
(2
x 2
4 ) 4
x
2
3)2 log 2 x 5 3 log x 2
1
4) log 9 x 2 (6 2 x x )
2
5) x lg x 3 0,01
2
9.
Решите уравнения;.
loq
2
(4 x 3) 3
loq (2x 3) loq ( x 4)
6
6
loq ( x 5) loq (2x 1) 2
3
loq
x
3
3
( x 2 3x 5) loq (7 2 x)
loq3 x
3
81
10.
Найти корни уравнения;.
loq x 4 x
3
11.
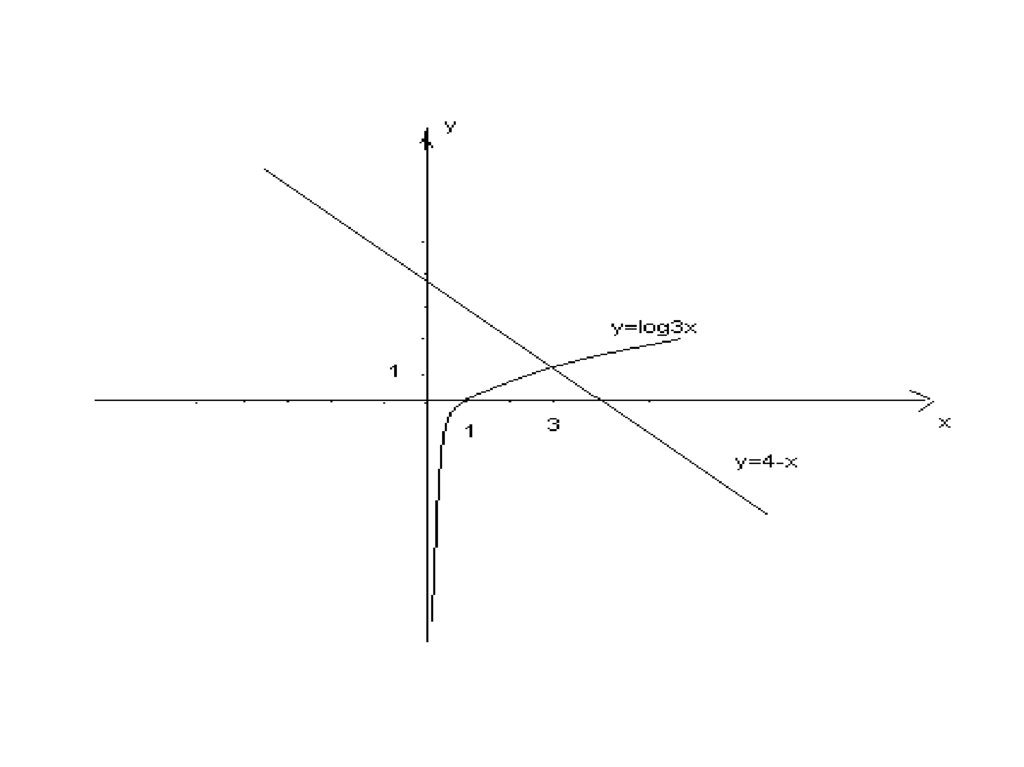
Для решения ЛУ графическим методом надо построить водной и той же системе координат графики функций,
стоящих в левой и правой частях уравнения и найти абсциссу
их точки пересечения
Найти корни уравнения
loq
3
x 4 x
Так как функция у= log3 х возрастающая, а функция у =4-х
убывающая на (0; + ∞ ),то заданное уравнение на этом
интервале имеет один корень.
12.
13.
Логарифмические неравенстваРешение неравенств, содержащих неизвестное под знаком
логарифма, основано на следующих теоремах:
log a f ( x ) g ( x )
f ( x ) a g ( x ) , если
log a f ( x ) g ( x )
f ( x ) a g ( x ) , если
log a f ( x) log a g ( x)
f ( x) g ( x), если
0 а 1
a 1
f ( x) 0
f ( x) 0
f ( x) 0
q ( x) 0
q ( x) 0
g ( x) 0
а 1
log a f ( x) log a g ( x)
f ( x) g ( x), если
0 a 1
f ( x) 0
g ( x) 0
14.
Решите неравенства.
loq
loq
2
1
2
x 2
x 2
loq x 2
loq (6 x) 2
loq (2 x 1) loq ( x 4)
2
4
3
3
3
15.
.loq x loq 72 loq 8
3
3
3
lq( x 8) lq(2 9x)
2
2
loq x 4 loq x 3
2
2







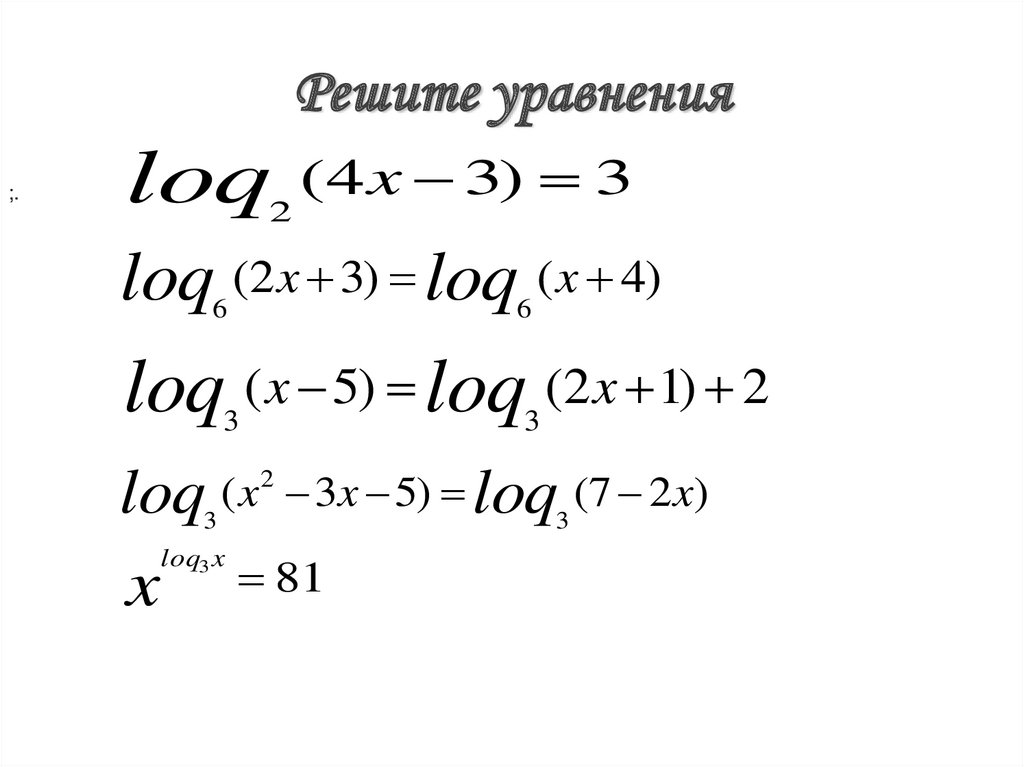



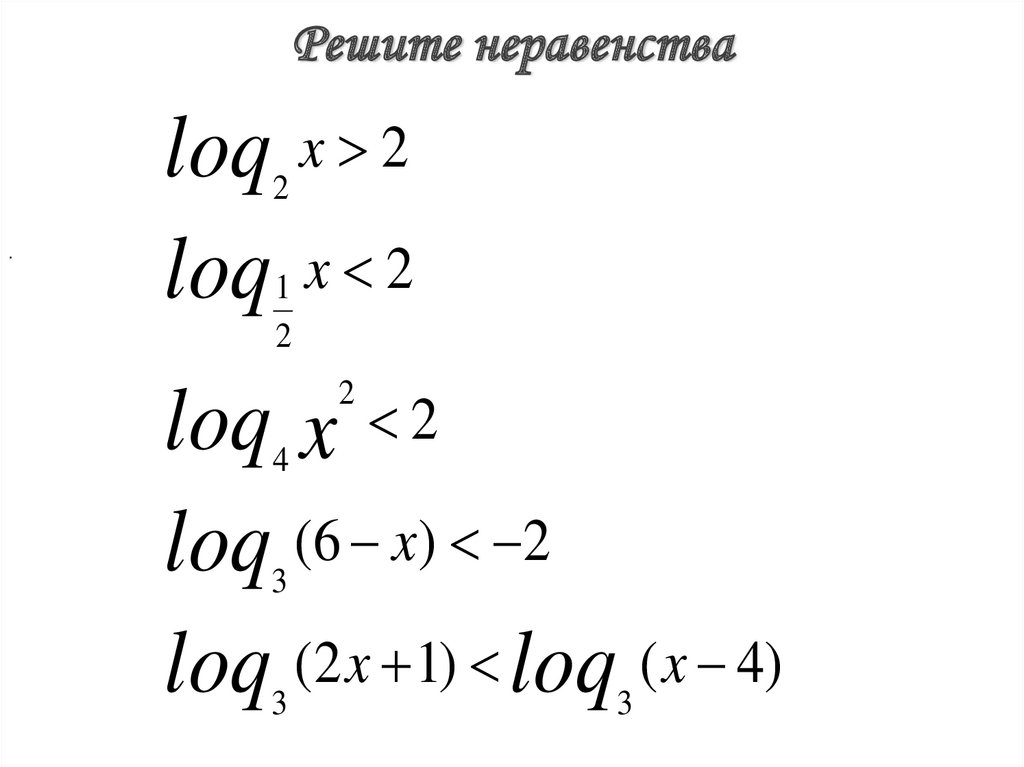
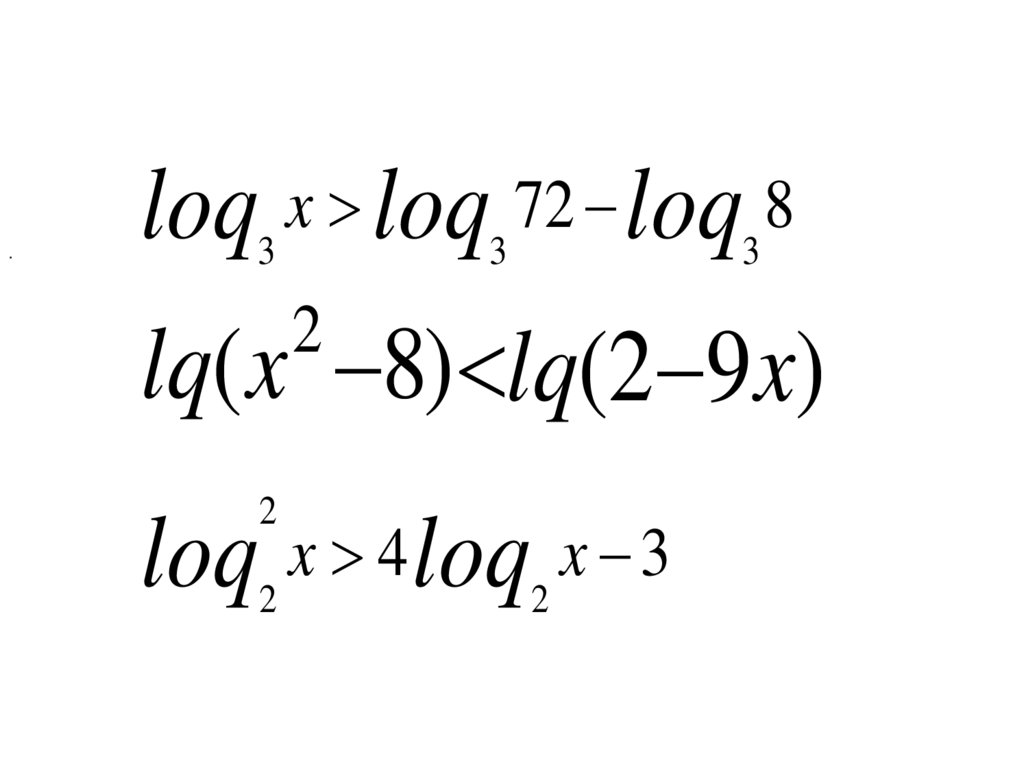
 Математика
Математика








