Похожие презентации:
Уравнение линии
1.
2.
Уравнением линии на плоскости XOYназывается уравнение, которому удовлетворяют
координаты x и y каждой точки этой линии
и не удовлетворяют координаты любой точки,
не лежащей на этой линии.
В общем случае уравнение линии может быть
записано в виде
F ( x, y) 0
или
y f (x)
3.
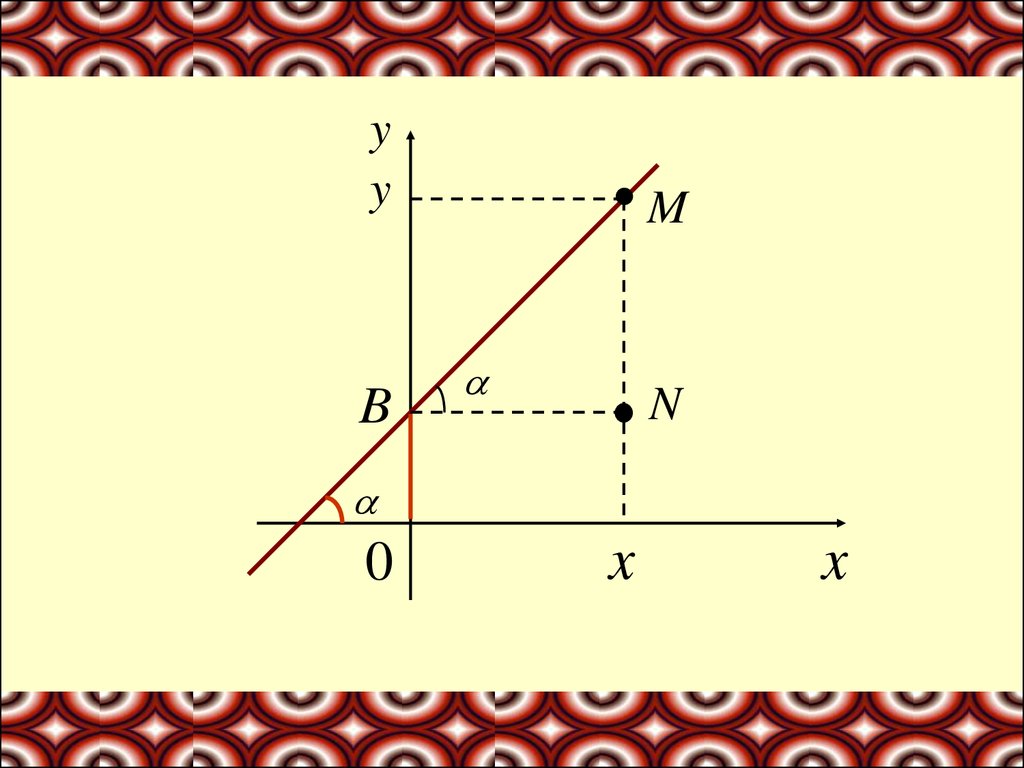
Пусть задана прямая, пересекающая ось у в точкеВ (0,в) и образующая с осью х угол α 0
2
Выберем на прямой произвольную точку
М(х,у).
4.
yy
B
M
N
0
x
x
5.
Координаты точки N (x,в). Из треугольника BMN:MN y b
tg
k
NB
x
k – угловой коэффициент прямой.
y kx b
1
6.
Рассмотрим частные случаи:b 0
1
-
y kx
уравнение прямой,
начало координат.
2
проходящей
через
0 tg 0 y b
- уравнение прямой, параллельной оси х.
7.
32
tg
2
- не существует
т.е. у вертикальной прямой нет углового
коэффициента.
Уравнение прямой, параллельной оси у, в этом
случае имеет вид
x a
где а – отрезок, отсекаемый прямой на оси х.
8.
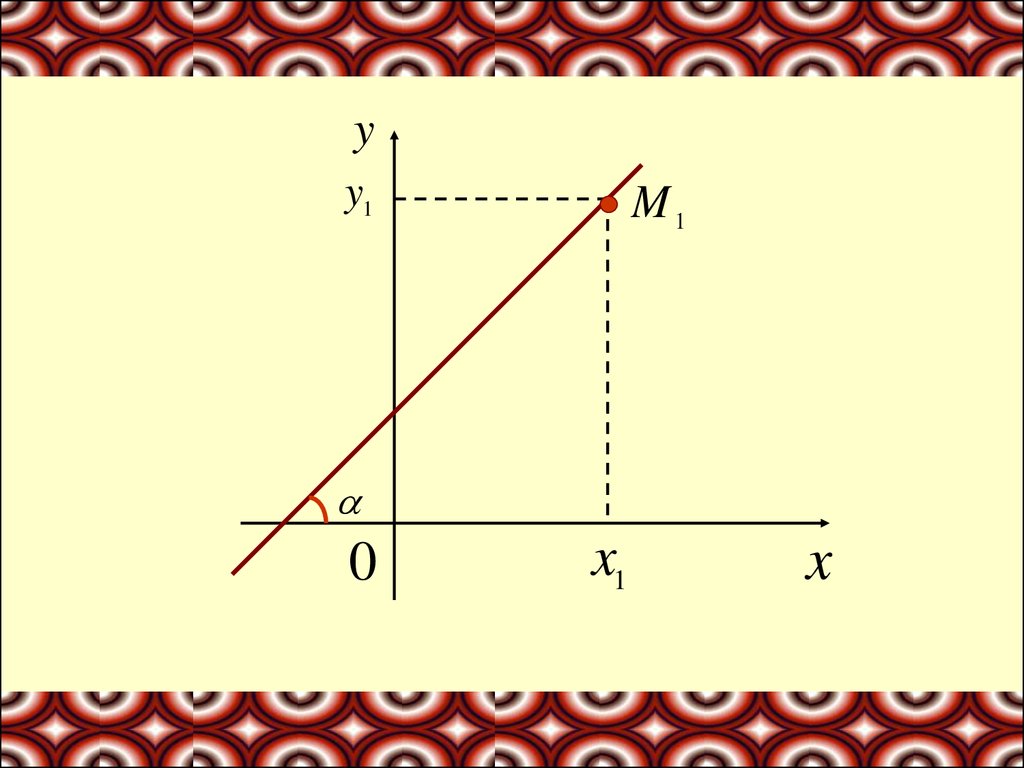
Пусть задана прямая, проходящая через заданнуюточку
M 1 ( x1 , y1 )
и образующая с осью х угол α
2
9.
yy1
M1
0
x1
x
10.
Т.к. точка М1 лежит на прямой, ее координатыдолжны удовлетворять уравнению (1):
y1 kx1 b
Вычитаем это уравнение из уравнения (1):
y y1 k ( x x1 )
2
11.
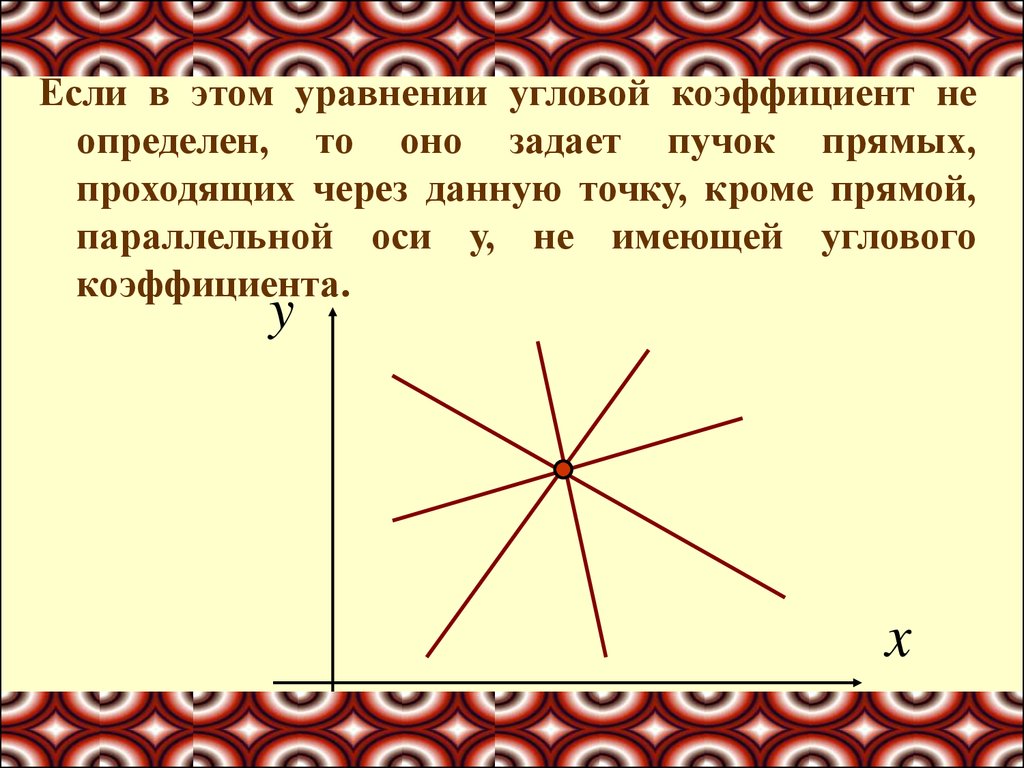
Если в этом уравнении угловой коэффициент неопределен, то оно задает пучок прямых,
проходящих через данную точку, кроме прямой,
параллельной оси у, не имеющей углового
коэффициента.
y
x
12.
Пусть задана прямая, проходящая через две точки:M 1 ( x1 , y1 )
M 2 ( x2 , y2 )
Запишем уравнение пучка прямых, проходящих
через точку М1:
y y1 k ( x x1 )
13.
Т.к. точка М2 лежит на данной прямой, подставимее координаты в уравнение пучка прямых:
y2 y1 k ( x2 x1 )
y2 y1
k
x2 x1
Подставляем k в уравнение пучка прямых. Тем
самым мы выделяем из этого пучка прямую,
проходящую через две данные точки:
14.
илиy2 y1
x x1
y y1
x2 x1
y y1
x x1
y2 y1 x2 x1
3
15.
ПРИМЕР.Составить уравнение прямой,
проходящей через точки А(-5,4) и
В(3,-2).
16.
РЕШЕНИЕ.Подставляем координаты точек в уравнение
прямой, проходящей через две точки.
y 4 x 5
2 4 3 5
6
y 4 ( x 5)
8
3
1
y x
4
4
17.
Пусть задана прямая,отсекающая на осях
координат отрезки, равные а и в.
Это значит, что она проходит через точки
A(a,0)
B(0, b)
Найдем уравнение этой прямой.
18.
yB
b
A
0
a
x
19.
Подставим координаты точек А и В в уравнениепрямой, проходящей через две точки (3):
y 0 x a
b 0 0 a
y x a
b a
x y
1
a b
y
x
1
b a
4
20.
ПРИМЕР.Составить уравнение прямой,
проходящей через точку А(2,-1) если она
отсекает от положительной полуоси у
отрезок, вдвое больший, чем на
положительной полуоси х.
21.
РЕШЕНИЕ.По условию задачи,
b 2a
x
y
1
Подставляем в уравнение (4):
a 2a
Точка А(2,-1) лежит на этой прямой, следовательно
ее координаты удовлетворяют этому уравнению:
2 1
1
a 2a
1 4
1
2a
3
a
2
x y
1
1.5 3
22.
Рассмотрим уравнение:Ax By C 0
5
Рассмотрим частные случаи этого уравнения и
покажем,
что
при
любых
значениях
коэффициентов А, В (не равных нулю
одновременно)
и С, это уравнение есть
уравнение прямой на плоскости.
23.
1B 0
Тогда уравнение (5) можно представить в виде:
A
C
y x
B
B
Обозначим:
A
k
B
C
b
B
Тогда получаем уравнение (1):
y kx b
24.
B 02
A 0
C 0
Тогда уравнение имеет вид:
A
y x
B
- уравнение прямой, проходящей через начало
координат.
3
B 0
A 0
C 0
C
Получаем уравнение: y
B
- уравнение прямой, параллельной оси х.
25.
4B 0
A 0
C 0
Тогда уравнение имеет вид:
- уравнение оси х.
5
B 0
A 0
Получаем уравнение:
y 0
C 0
C
x
A
- уравнение прямой, параллельной оси у.
26.
6B 0
A 0
C 0
Тогда уравнение имеет вид:
x 0
- уравнение оси у.
Таким
образом,
при
любых
значениях
коэффициентов А, В (не равных нулю
одновременно)
и С,
уравнение (5) есть
уравнение прямой на плоскости.
Это























 Математика
Математика








