Антагонистические игры

1.

Тема 1. Антагонистические игры
Введение
1. Матричные игры в чистых стратегиях
2. Мажорирование (доминирование)
стратегий

2.

Введение
Основные вопросы теории игр
1. Какие свойства стратегий следует считать
признаками оптимальности?
2. Существуют ли стратегии игроков, которые
обладали бы свойствами
оптимальности?
3. Как определить оптимальные стратегии,
если они существуют?

3.

1. Матричные игры в чистых стратегиях
Антагонистическая игра представляет
собой математическую модель принятия
решения в условиях противоположности
интересов

4.

«Игра в орлянку»
- игра двух лиц с нулевой суммой
?
?
«Решка»
«Орел»

5.

Матрица игры
Возможные
чистые стратегии
а1 (орел)
а2 (решка)
b1
(орел)
b2
(решка)
1
-1
-1
1
1 1
A
1 1

6. «Дилемма заключенного»

- игра с ненулевой суммой
Два преступника ожидают приговора суда за совершенное злодеяние. Адвокат
конфиденциально предлагает каждому из преступников облегчить его участь (и
даже освободить!), если он сознается и даст показания против сообщника,
которому грозит угодить в тюрьму за совершенное преступление на 10 лет. Если
никто не сознается, то обоим угрожает заключение на определенный срок
(допустим, 1 год) по обвинению в незначительном преступлении. Если
сознаются оба преступника, то, с учетом чистосердечного признания, им
обоим грозит попасть в тюрьму на 5 лет. Каждый заключенный имеет на выбор 2
стратегии: не сознаваться или сознаваться, выдав при этом сообщника.
Сознаться
или
нет??????
Сознаться
или
нет??????

7. «Дилемма заключенного»

Матрица "выигрышей" для обоих игроков
Стратегии 2-го игрока
Сознаться Не сознаться
0, 10
Сознаться
5, 5
1, 1
Не сознаться 10, 0
Стратегии l-го игрока

8.

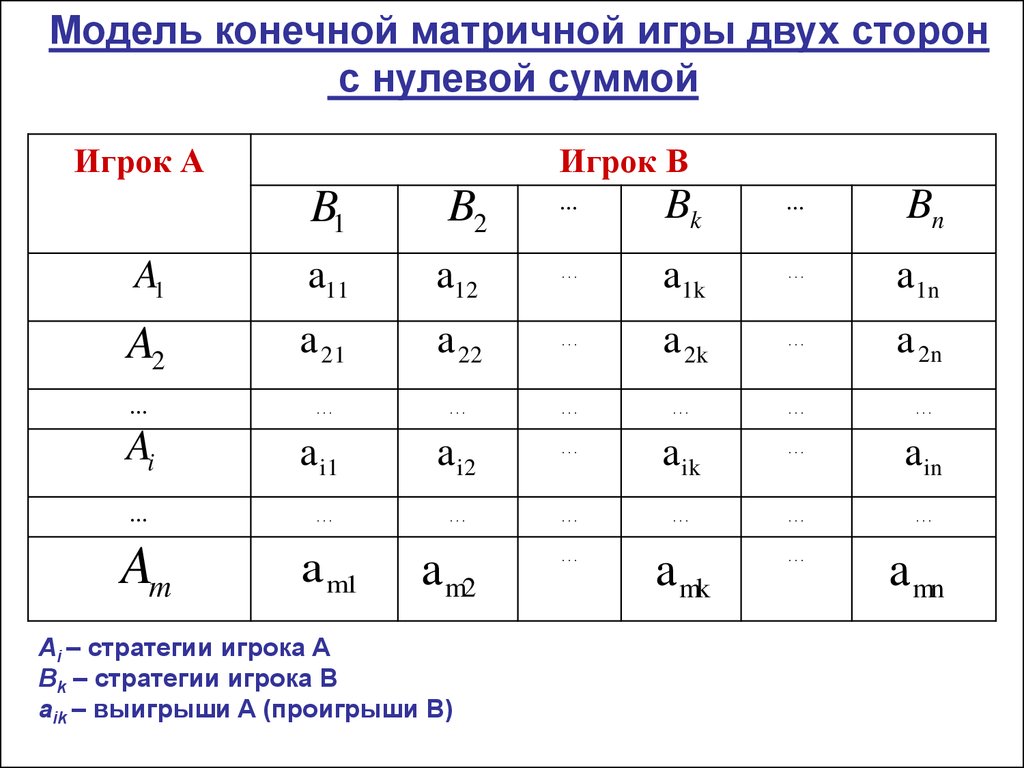
Модель конечной матричной игры двух сторон
с нулевой суммой
Игрок А
Игрок В
…
Bk
…
Bn
a12
…
a1k
…
a1n
a 21
a 22
…
a 2k
…
a 2n
…
…
…
…
…
…
…
Ai
a i1
a i2
…
a ik
…
a in
…
…
…
…
…
…
…
a mk
…
B1
B2
A1
a11
A2
Am
a m1
a m2
Ai – стратегии игрока A
Bk – стратегии игрока В
аik – выигрыши A (проигрыши B)
…
a mn

9.

Игрок А
B1
A1
A2
…
Ai
…
Am
Минимумы
Игрок В
B2
…
…
Bk
…
a11
a 21
a 22
…
…
a i1
a i2
…
…
a m1
a m2
Максимумы max a max ai 2
i1
столбцов
…
a1k
a12
…
…
…
…
…
a ik
…
…
…
a 2k
…
…
Bn
…
…
…
a mk
min max aik
k
i
…
строк
a1n
min a1k
a 2n
min a 2k
…
a in
…
max min aik
i
k
…
…
a mn
min a mk
max ain

10.

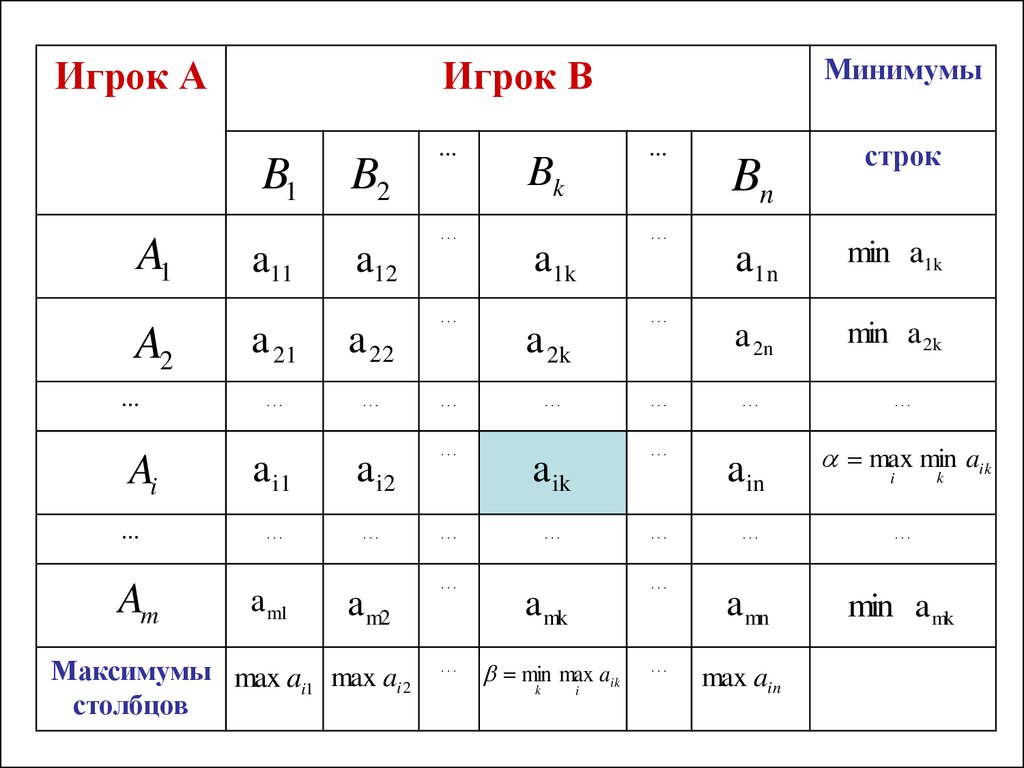
Нижняя цена игры
Верхняя цена игры
min max aik
max min aik
i
Аi
k
k
- максиминная
стратегия
Bk
i
- минимаксная
стратегия
Цена игры
V
Игра с седловой точкой
V
Аi
(
Аi
Bk
оптимальные
стратегии
, Bk ) – решение игры
и
-
aik - седловая точка, ее значение - цена игры

11. Пример

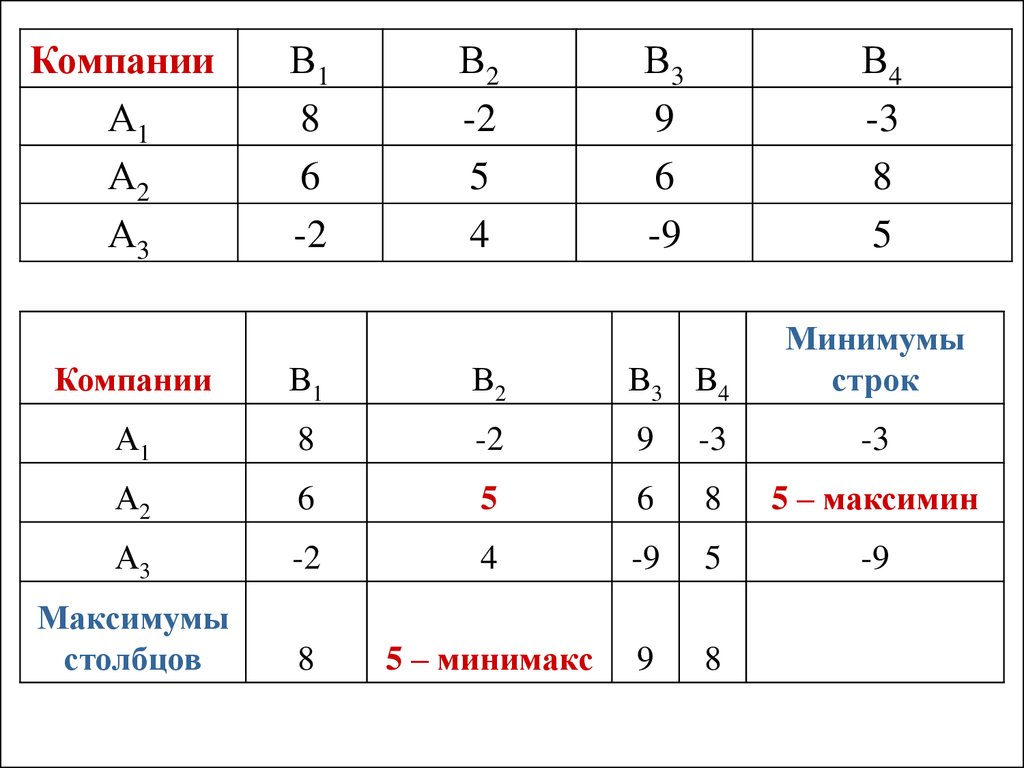
Две компании А и В продают два вида лекарств против гриппа.
Компания А рекламирует продукцию на радио (A1), телевидении (А2) и
в газетах (А3). Компания В, в дополнение к использованию радио (B1),
телевидения (В2) и газет (В3) рассылает также по почте брошюры
(В4.). В зависимости от умения и интенсивности проведения
рекламной кампании, каждая из компаний может привлечь на свою
сторону часть клиентов конкурирующей компании.
«Радио»
«Телевидение»
Компания «А»
«Газеты»
«Брошюры»
Компания «В»
?

12.

Компании
А1
А2
А3
В1
8
6
-2
В2
-2
5
4
В3
9
6
-9
В4
-3
8
5
Минимумы
строк
Компании
В1
В2
В3 В4
А1
8
-2
9
-3
-3
А2
6
5
6
8
5 – максимин
А3
-2
4
-9
5
-9
Максимумы
столбцов
8
5 – минимакс
9
8

13.

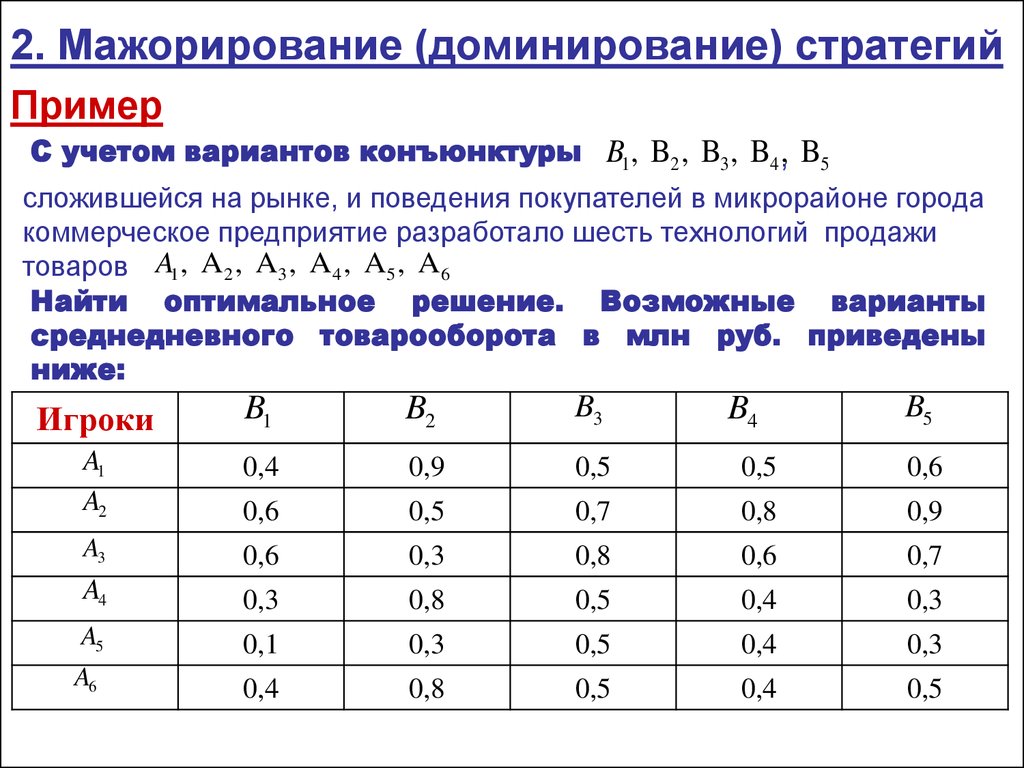
2. Мажорирование (доминирование) стратегий
Пример
С учетом вариантов конъюнктуры B1, B2 , B3 , B4 ,, B5
сложившейся на рынке, и поведения покупателей в микрорайоне города
коммерческое предприятие разработало шесть технологий продажи
товаров A1 , A 2 , A3 , A 4 , A5 , A6
Найти оптимальное решение. Возможные варианты
среднедневного товарооборота в млн руб. приведены
ниже:
B5
Игроки
B1
B2
B3
A1
A2
0,4
0,9
0,5
0,5
0,6
0,6
0,5
0,7
0,8
0,9
A3
0,6
0,3
0,8
0,6
0,7
A4
0,3
0,8
0,5
0,4
0,3
A5
0,1
0,3
0,5
0,4
0,3
A6
0,4
0,8
0,5
0,4
0,5
B4

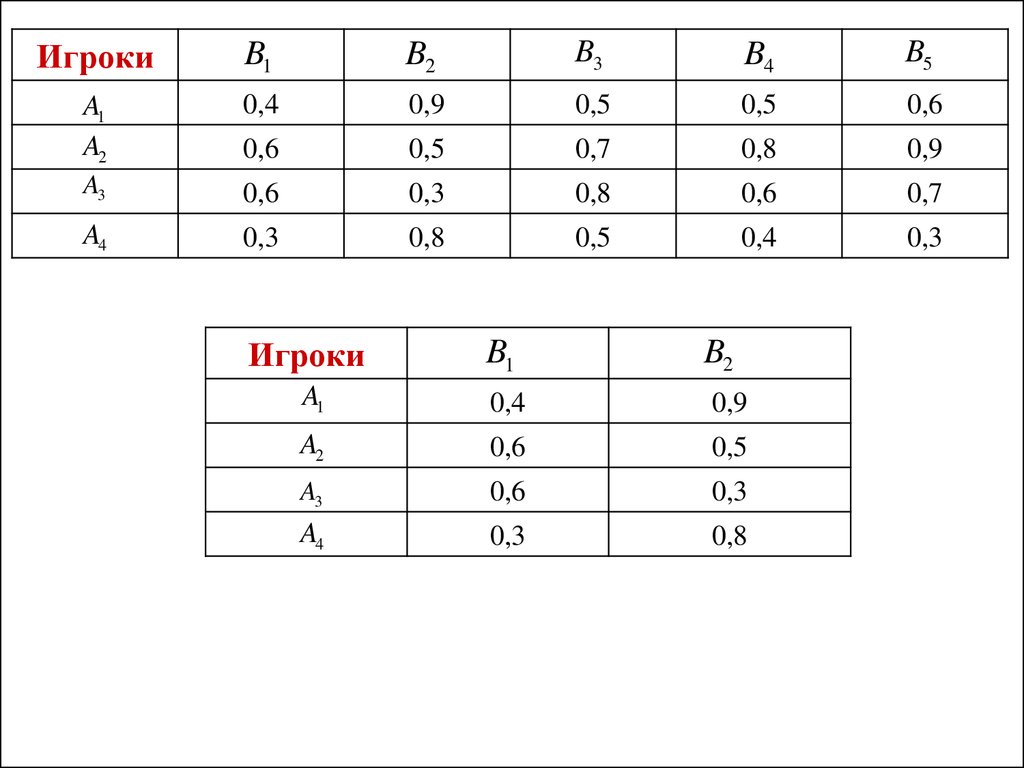
14.

Игроки
B1
B2
B3
B4
B5
A1
A2
0,4
0,9
0,5
0,5
0,6
0,6
0,5
0,7
0,8
0,9
A3
0,6
0,3
0,8
0,6
0,7
A4
0,3
0,8
0,5
0,4
0,3
Игроки
B1
B2
A1
0,4
0,9
A2
0,6
0,5
A3
0,6
0,3
A4
0,3
0,8

15.

Игроки
B1
B2
A1
0,4
0,9
A2
0,6
0,5
Игроки
B1
B2
Минимумы
строк
A1
0,4
0,9
0,4
A2
0,6
0,5
0,6
0,9
Максимумы
столбцов
0,5 0,6
0,5