Колебательные процессы

1.

РАЗДЕЛ 4
КОЛЕБАНИЯ И ВОЛНЫ.
ВОЛНОВАЯ ОПТИКА
Тема 23
КОЛЕБАТЕЛЬНЫЕ ПРОЦЕССЫ
Лекция 1

2.

Цель лекции – ознакомиться с общими характеристиками
колебательных процессов и методами количественного
описания гармонических колебаний.
Вопросы лекции:
1. Классификация колебательных процессов и их
общие характеристики.
2. Линейный гармонический осциллятор. Свободные
механические колебания.
3. Свободные электромагнитные колебания. LC –
контур.
Литература:
БЭУ; Доп. [1, стр. 208-220]; [2, стр. 168-184]
Техническое обеспечение:
Комплект мультимедийных средств обучения.
База данных анимаций физических процессов.

3.

23.1.1. Классификация колебательных
процессов и их общие характеристики.
Колебательные процессы (колебания) – это любые
физические процессы, повторяющиеся во времени.
Физическая система, участвующая в таких процессах,
называется колебательной системой или осциллятором.
Классификация колебательных процессов
► по физической природе колебательной системы:
– механические колебания (повторяющиеся движения тел);
– электромагнитные колебания (повторяющиеся изменения
электрического и магнитного полей);
– термодинамические колебания (циклические процессы в
макроскопических системах).

4.

► по виду зависимости параметров колебаний от времени :
– периодические колебания (значения параметров
повторяются через одинаковые промежутки времени);
– непериодические колебания (значения параметров
повторяются через разные промежутки времени).
► по характеру внешнего воздействия на колебательную
систему:
– свободные колебания (возникают в системе вследствие
однократного начального внешнего воздействия);
– вынужденные колебания (возникают в системе
вследствие повторяющегося внешнего воздействия).
Особое место среди всех колебательных процессов
занимают периодические колебания.
(ограничимся их рассмотрением!)

5.

Общие характеристики периодических колебаний:
Для любой переменной физической величины S при
периодических колебаниях справедливо равенство:
s (t ) s (t T )
(23.1)
Т - период колебаний
Период колебаний – это наименьший промежуток
времени, по истечении которого, значения физической
величины повторяются.
Пример:
периодическое колебание
давления в точке волнового
поля звуковой волны.
осциллограмма
Р
t
T

6.

Частота колебаний – это число полных колебаний,
совершаемых за единицу времени.
1
T
Единица частоты:
(23.2)
1 с 1 1 Гц
Циклическая (круговая) частота – это число полных
колебаний, совершаемых за 2 секунд.
2
T
(23.3)
Единица циклической частоты:
1 с 1
Простейшими периодическими колебаниями являются
гармонические колебания.

7.

23.1.2. Линейный гармонический осциллятор.
Свободные механические колебания.
При гармоническом колебании уравнение (23.1) имеет вид:
s (t ) smax sin ( 0t 0 )
s
или
осциллограмма
smax
s (t ) smax cos ( 0t 0 )
амплитуда
колебаний
фаза
колебаний
0 - начальная фаза
t
T
(в момент времени t =0)
0 и smax зависят от
начальных условий!
0 собственная частота колебаний (характеристическая
величина для данной колебательной системы).

8.

Гармонические колебания всегда являются свободными и
возникают в системах, имеющих положение устойчивого
равновесия.
Линейный гармонический осциллятор это колебательная
система, совершающая одномерные свободные колебания.
Свободные механические колебания
Механические свободные колебания это повторяющиеся
движения точки (тела или системы тел) относительно
положения устойчивого равновесия.
Механический
линейный
осциллятор
маятником. Различают маятники:
► пружинный;
► математический;
► физический.
называется

9.

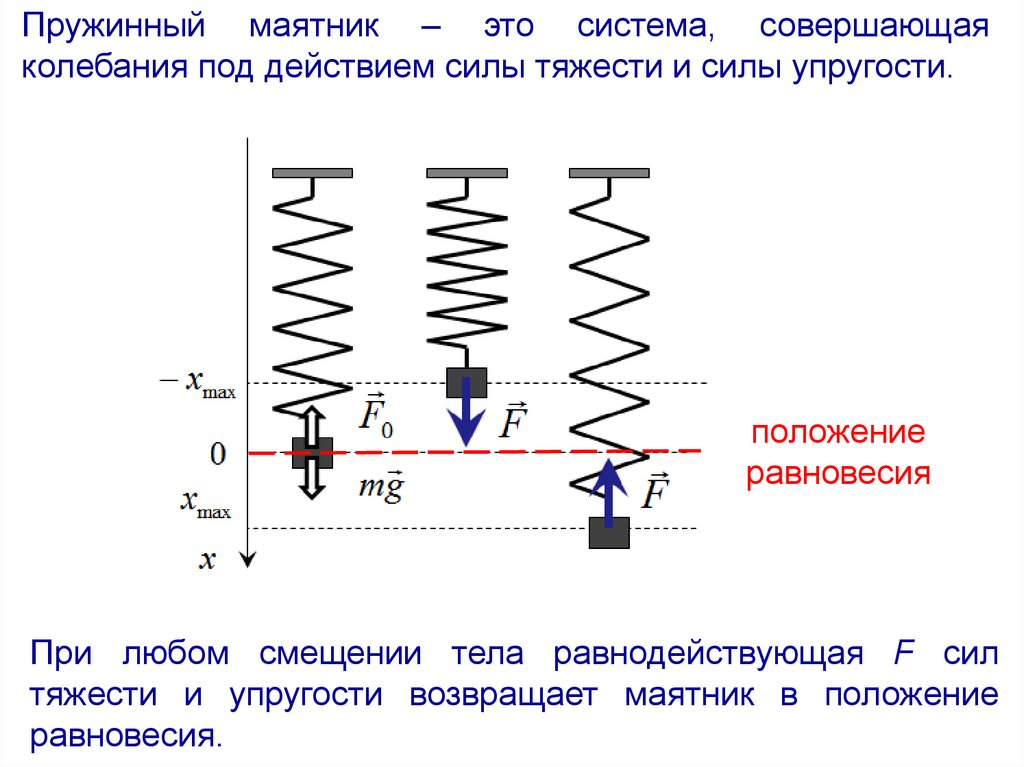
Пружинный маятник – это система, совершающая
колебания под действием силы тяжести и силы упругости.
положение
равновесия
При любом смещении тела равнодействующая F сил
тяжести и упругости возвращает маятник в положение
равновесия.

10.

Возвращающая (квазиупругая) сила
По определению
F kx ma
d 2x k
x 0
2
dt
m
d 2x
a 2
dt
обозначим
Получим
d 2x
2
0x 0
2
dt
решение
k
02
m
линейное
однородное
второго порядка.
x A cos( 0t 0 )
ДУ
(23.4)
уравнение колебаний маятника (смещение тела)
А xmax
где
k
0
m
амплитуда колебаний
собственная частота колебаний

11.

Кинематические
маятника:
и
динамические
характеристики
1) скорость
dx
v
A 0 sin ( 0 t 0 )
dt
(23.5)
2) ускорение
d2 x
а 2 A 02 cos ( 0 t 0 )
dt
(23.6)
3) импульс
p mv mA 0 sin ( 0 t 0 )
(23.7)
4) сила
F mа mA 02 cos ( 0 t 0 )
(23.8)
Из (23.5)
v max A 0
Из (23.6)
аmax A 02
и
а 02 х

12.

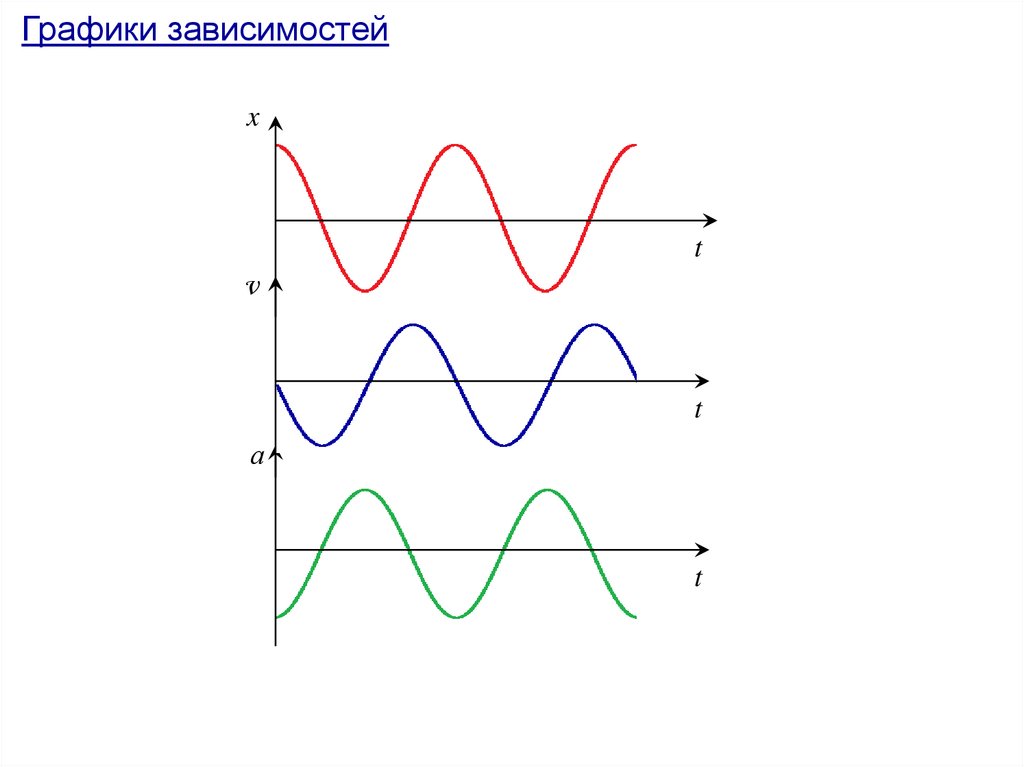
Графики зависимостей
x
t
v
t
а
t

13.

Энергия колебаний маятника:
2
1) кинетическая
mv
mA2 02 2
Wк
sin ( 0 t 0 )
2
2
(23.9)
2
kx
mA2 02
2) потенциальная Wп
cos 2 ( 0 t 0 )
2
2
(23.10)
Система консервативна, т.е. полная энергия не изменяется!
mA2 02
W Wк Wп
2
W
Wп
(23.11)
закон сохранения
энергии
Wк
t

14.

23.1.3. Свободные электромагнитные колебания.
LC – контур.
Свободные
электромагнитные
колебания
–
это
повторяющиеся во времени взаимные превращения
электрического и магнитного полей.
C
L C
qmax 0; I 0
L
q 0; I max
C
L
qmax 0; I 0

15.

По 2-му правилу Кирхгофа:
U Ei
ЭДС самоиндукции по закону Фарадея:
dI
Ei L
dt
Учтем:
Получим
где
q CU
d 2U
U LС 2
dt
d 2U
1
U 0
2
LC
dt
обозначим
Получим
d 2U
2
0U 0
2
dt
dq
I
dt
1
02
LC
линейное
однородное
второго порядка.
ДУ

16.

U U max cos( 0t 0 )
решение
амплитуда колебаний
напряжения
U max
где
0
1
LC
(23.12)
собственная частота LC-контура
Заряд на обкладках конденсатора:
q qmax cos( 0t 0 )
где
qmax CU max
(23.13)
Ток отстает по фазе от напряжения:
dq
I
I max sin( 0t 0 )
где
dt
I max 0CU max
(23.14)

17.

Графики зависимостей
q;U
U (t )
q (t )
t
I
I (t )
t

18.

Энергия колебаний контура:
1) электрического поля
CU 2 q2
Wэл
2
2C
(23.15)
LI2
Wм
2
(23.16)
2) магнитного поля
Система консервативна, т.е. полная энергия не изменяется!
2
2
C U max
qmax
L I max
W Wэл Wм
2
2C
2
закон сохранения энергии
2
(23.17)

19.

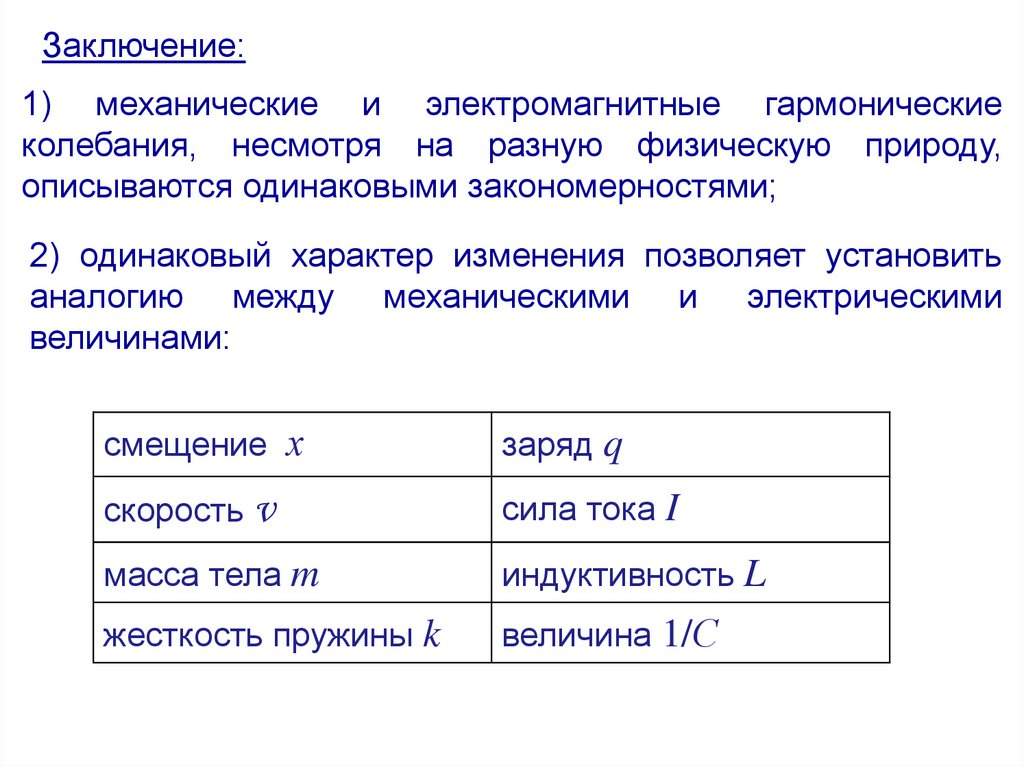
Заключение:
1) механические и электромагнитные гармонические
колебания, несмотря на разную физическую природу,
описываются одинаковыми закономерностями;
2) одинаковый характер изменения позволяет установить
аналогию между механическими и электрическими
величинами:
cмещение х
заряд q
cкорость v
cила тока I
масса тела m
индуктивность L
жесткость пружины k
величина 1/С