Похожие презентации:
Соотношения между сторонами и углами прямоугольного треугольника
1. СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА
* СООТНОШЕНИЯ МЕЖДУСТОРОНАМИ И УГЛАМИ
ПРЯМОУГОЛЬНОГО
ТРЕУГОЛЬНИКА
2.
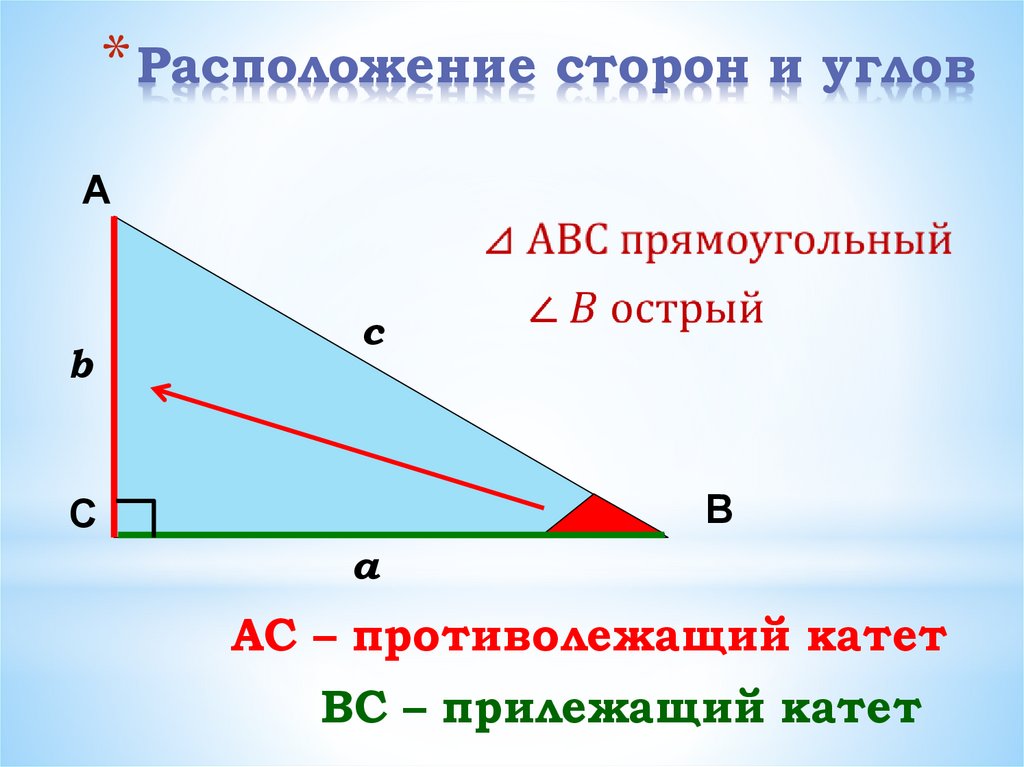
3. Расположение сторон и углов
* Расположение сторон и угловА
b
c
В
С
a
AС – противолежащий катет
ВС – прилежащий катет
4. Расположение сторон и углов
* Расположение сторон и угловА
c
b
С
a
В
ВС - противолежащий катет
АС – прилежащий катет
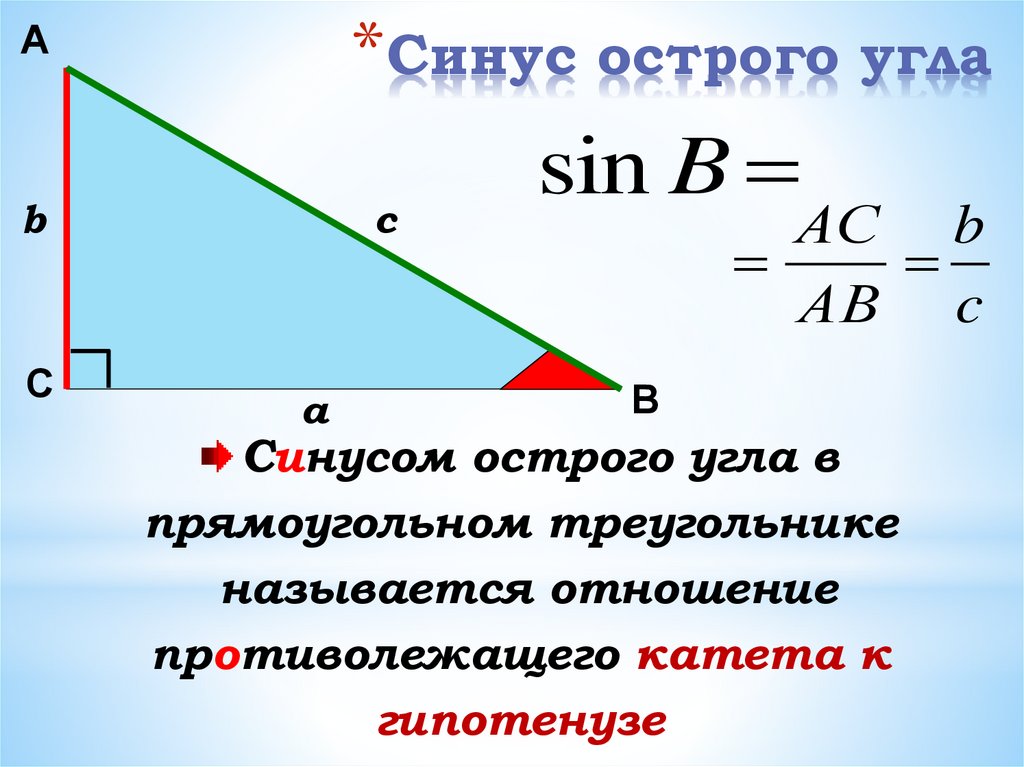
5. Синус острого угла
*Синус острого углаА
b
С
c
a
sin B
АС b
АВ c
В
Синусом острого угла в
прямоугольном треугольнике
называется отношение
противолежащего катета к
гипотенузе
6.
АКосинус острого угла
cos B
c
ВС
a
АВ
c
b
С
a
В
Косинусом острого угла в
прямоугольном треугольнике
называется отношение
прилежащего катета к
гипотенузе
7. Тангенс острого угла
Аb
С
* Тангенс острого угла
tgB
c
АС b
а
ВС
a
В
Тангенсом острого угла в
прямоугольном треугольнике
называется отношение
противолежащего катета к
прилежащему катету
8. Повторим
* ПовторимА
c
b
С
В
a
sinA
BС
a
AВ
c
cosA
AС
b
AВ
c
tgA
BС
a
AC
b
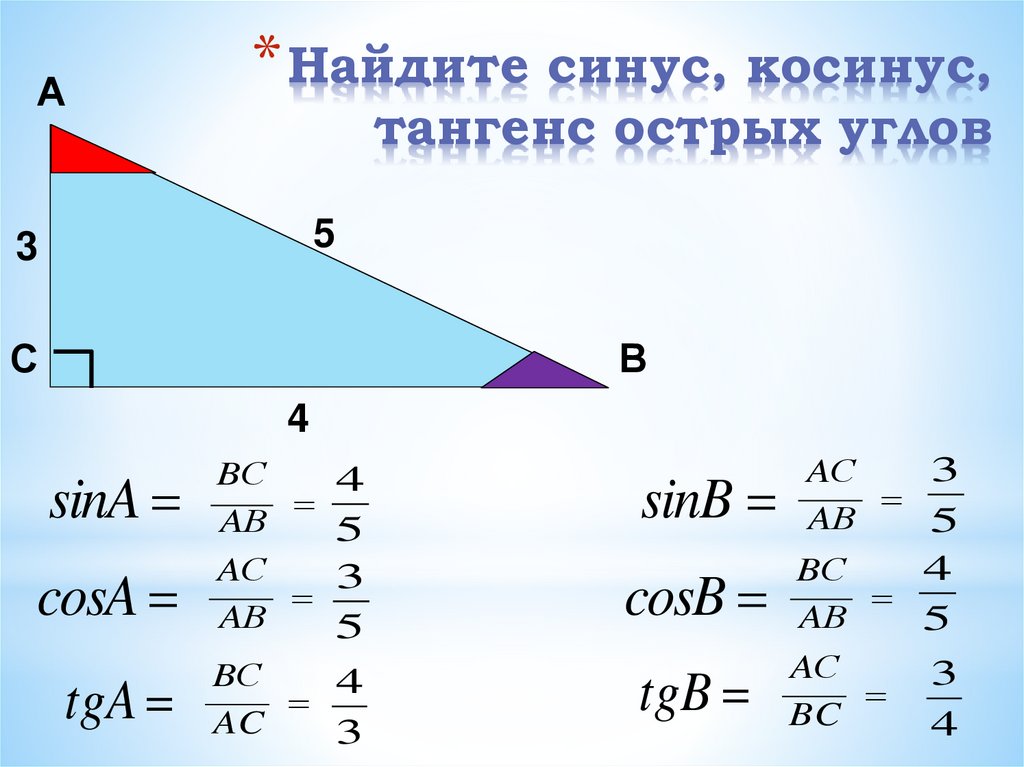
9. Найдите синус, косинус, тангенс острых углов
А* Найдите синус, косинус,
тангенс острых углов
5
3
В
С
4
sinA
cosA
tgA
BС
4
AВ
5
AС
3
AВ
5
BС
4
AC
3
sinB
cosB
tgB
3
AС
AВ
5
4
BС
AВ
5
AС
3
BC
4
10.
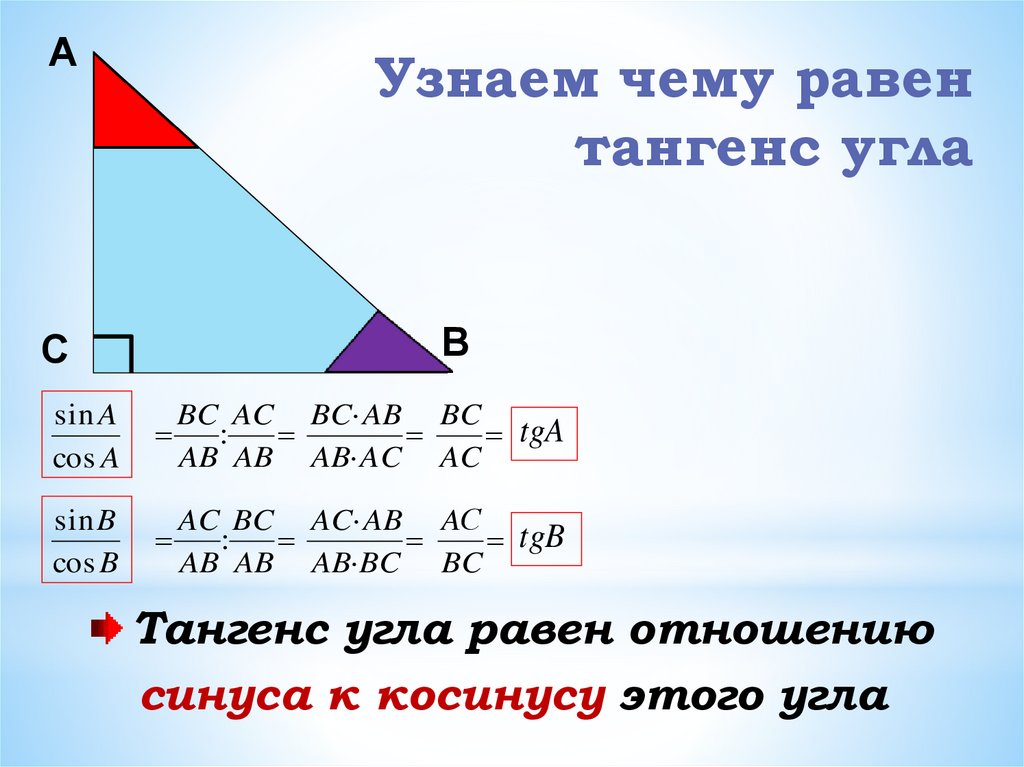
АУзнаем чему равен
тангенс угла
В
С
sin A
cos A
BC AC BC AB BC
:
tgA
AB AB AB AC AC
sin B
cos B
AC BC AC AB AС
:
tgB
AB AB AB BC BC
Тангенс угла равен отношению
синуса к косинусу этого угла
11.
АА1
С1
С
В1
В
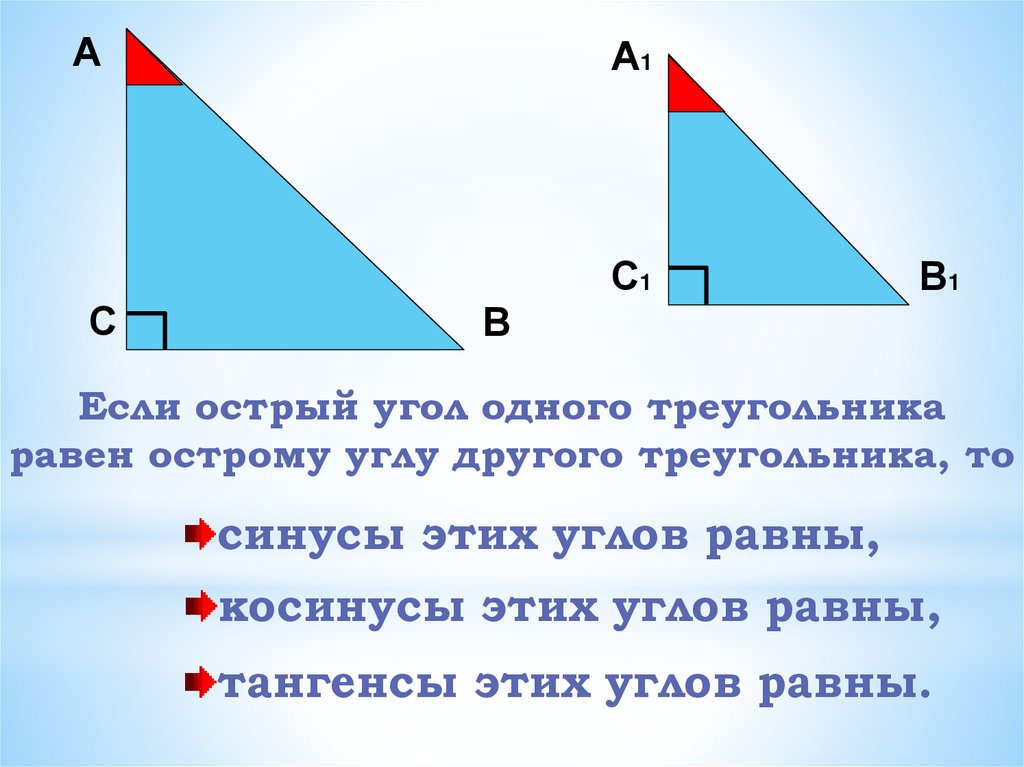
Если острый угол одного треугольника
равен острому углу другого треугольника, то
синусы этих углов равны,
косинусы этих углов равны,
тангенсы этих углов равны.
12.
Докажем равенствоА
sin A cos A 1
2
2
В
С
sinA
BС
AВ
cosA
AС
AВ
sin A cos A
2
2
AC
BA AC
BC
AB
1
2
2
2
2
AB
AB
AB
AB
2
2
2
2
2
13.
Равенствоsin cos 1
2
2
называется
основным
тригонометрическим
тождеством








 Математика
Математика








