Похожие презентации:
Геометрические приложения определенного интеграла
1. Геометрические приложения определенного интеграла
Для студентов 1 курса напр. «Мед.физика»2. Вычисление площадей плоских фигур
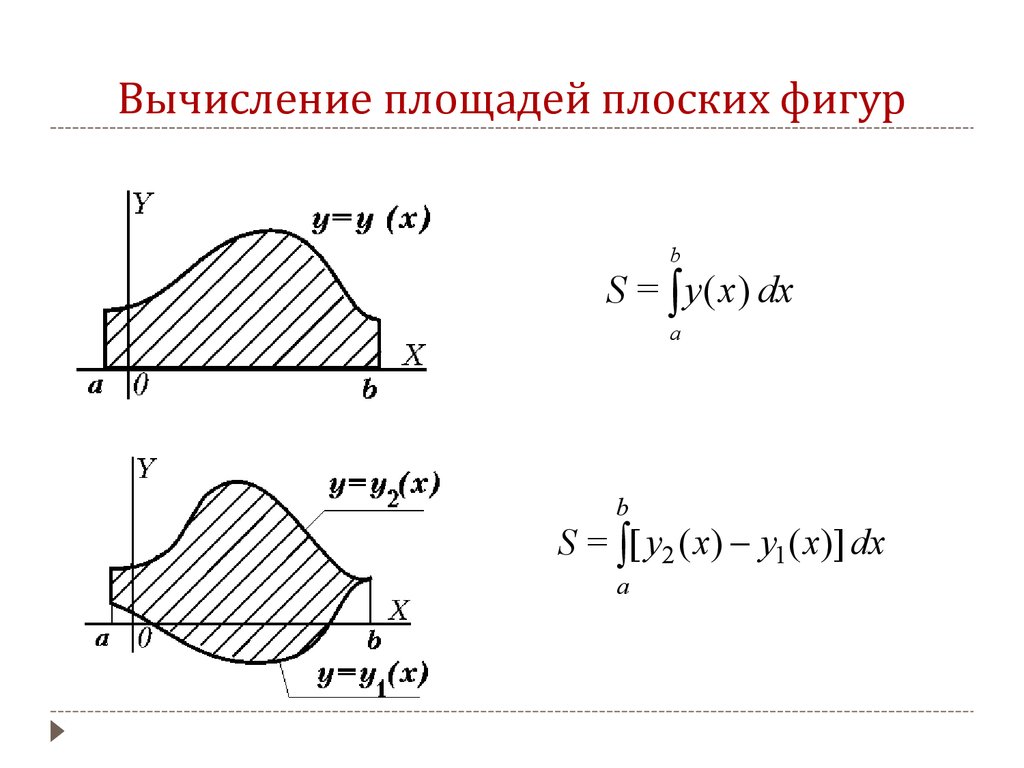
Вычисление площадеий плоских фигурb
S = y ( x) dx
a
b
S = [ y2 ( x) y1 ( x)] dx
a
3. Вычисление площадей плоских фигур
Вычисление площадеий плоских фигурd
S = x( y ) dy
c
d
S = [ x2 ( y ) x1 ( y )] dy
c
4. Пример. Найти площадь фигуры, ограниченной линиями
Пример. Наий ти площадь фигуры, ограниченноийлиниями xy = 2, y = 2 x, y = 3.
1. Строим фигуру.
d
2. Удобнее воспользоваться формулой
S = [ x2 ( y ) x1 ( y )] dy,
где
c
x1 ( y ) = 2/y, x2 ( y ) = y/2,
Значение
d = 3 определилось по построению
Значение
c = 2 получим, решая систему
ì xy = 2,
í
î y = 2 x.
3
y
y 2
9 4
5
3
S = dy = 2 ln y 2(ln 3 ln 2) 2 ln .
2 y
4
2
4
2 4 4
2
3
2
5. Вычисление площади криволинейного сектора в полярной системе координат
Вычисление площади криволинеий ного секторав полярноий системе координат
Y
( )
1
S 2 ( )d
2 1
2
1
2
X
Вычисление площади фигуры, заданноий
параметрически уравнениями
ì x = x(t )
L: í
,
t2
î y = y (t )
S = y (t ) x (t ) dt
t1
6. Вычисление объемов тел вращения
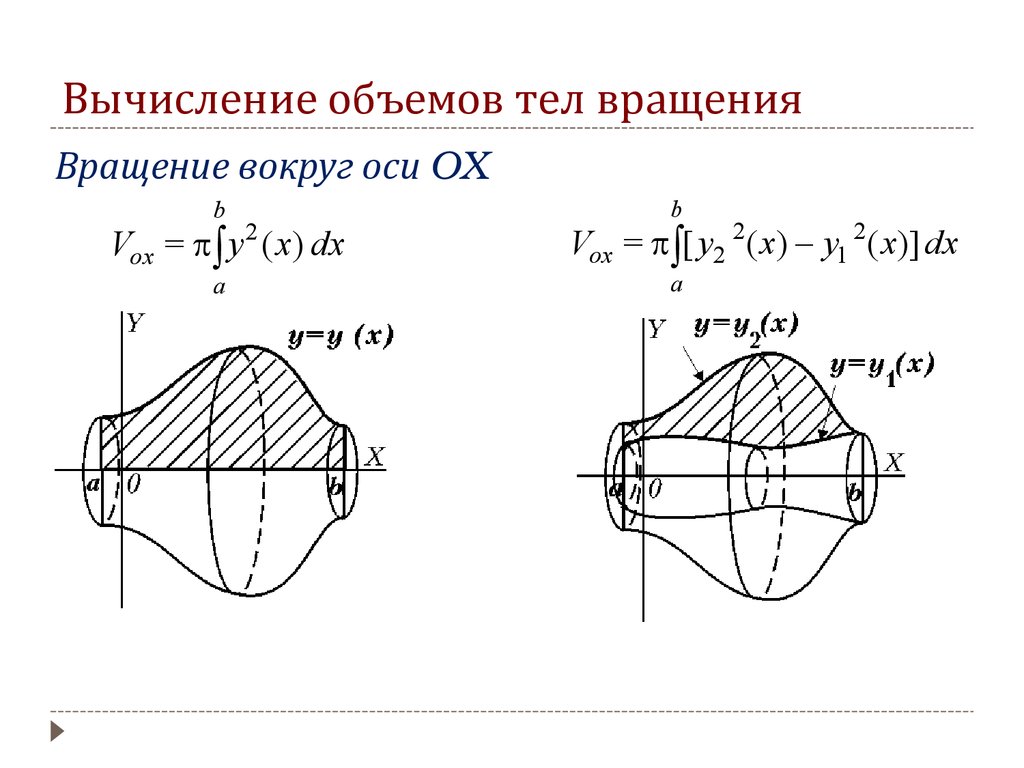
Вращение вокруг оси OXb
Vox = y 2 ( x) dx
a
b
Vox = [ y2 2( x) y1 2( x)] dx
a
7. Пример. Найти объем тела, полученного вращением вокруг оси ОХ кривой и ограниченного прямыми х=0 и у=1.
Пример. Наий ти объем тела, полученноговращением вокруг оси ОХ кривоий y = 2 x и
ограниченного прямыми х=0 и у=1.
b
Vox = [ y2 2( x) y1 2( x)] dx.
a
y2 ( x) = 1, y1 ( x) = 2 x .
Находим пределы интегрирования из условия
1/4
1/4
2 x = 1 x = 1/4.
2 14
Vox = [1 (2 x ) ] dx = (1 4 x) dx = ( x 2 x )
2
0
2
0
0
= .
8
8. Вычисление объемов тел вращения
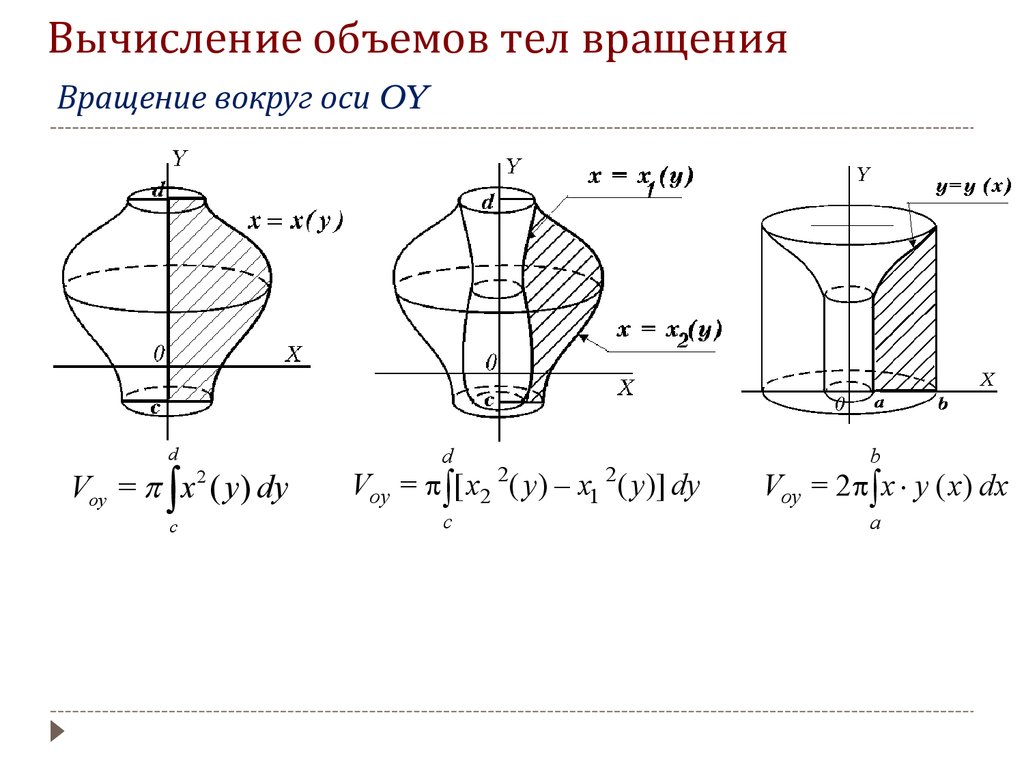
Вращение вокруг оси OYd
Voy = x ( y ) dy
2
c
d
2
2
Voy = [ x2 ( y ) x1 ( y )] dy
c
b
Voy = 2 x y ( x) dx
a
9. Вычисление длин дуг
bL : y f ( x), a x b
l
1 f ' ( x) dx
2
a
L : ( ),
l
( ) 2 ' ( ) 2 d
ì x x(t )
L: í
, t1 t t 2
î y y (t )
t2
l
t1
x' (t )
2
y ' (t ) dt
2
10. Пример. Найти длину части астроиды
Пример. Наий ти длину части астроидыì x = 2 cos 3 t ,
í
3
y
=
2
sin
t
î
L=
t2
0 t
2
xt2 yt2 dt.
t1
2
x
6
cos
t sin t ,
Предварительно находим t
2
yt 6 sin 2 t cos t ,
2
x y = 36 sin 2 t cos 4 t 36 sin 4 t cos 2 t = 36 sin 2 t cos 2 t sin 2 t cos 2 t =
t t
= 36 sin 2 t cos 2 t = 9 sin 2 2t.
2
2
x y = 3 sin 2t .
t t
/2
L=3 sin 2t dt=
0
3
3
3
cos 2t |0 /2 = cos cos 0 = 1 1 =3.
2
2
2







 Математика
Математика








