Лекция 13 по математике за 2 семестр

1.

Дисциплина: МАТЕМАТИКА
Раздел 3: Интегральное исчисление
Лекция №13
Определённые интегралы.
Применение интегралов в экономике
Разработчик: Бредихина Ольга Александровна

2.

3.2 Определённые интегралы
3.2.1 Основные понятия
Пусть на отрезке [a;b] задана функция y=f(x). Разобьём
этот отрезок на n частей точками a x0 x1 x2 ... xn 1 xn b.
На каждом малом отрезке [xi–1; xi], где i 1, n , выберём
точку ξi, найдём значение
функции в этой точке f(ξi) и
n
составим сумму J n f i xi , где xi xi xi 1.
i 1
Сумма Jn называется интегральной суммой для функции
y=f(x) на [a;b].
Определённым интегралом от функции f(x) на отрезке
[a;b] называется предел интегральной суммы Jn при
условии, что длина наибольшего
частичного отрезка Δxi
b
n
стремится к нулю, то есть f x dx lim
f x
a
n
max xi 0 i 1
i
i
где a – нижний предел интегрирования; b – верхний
предел интегрирования; f(x) – подынтегральная функция;
f(x)dx – подынтегральное выражение.

3.

3.2 Определённые интегралы
3.2.1 Основные понятия
Свойства определённого интеграла
Свойства определённого интеграла аналогичны свойствам
неопределённого интеграла. Дополнительные свойства:
b
c
b
1. f x dx f x dx f x dx , где c a; b ;
a b
2.
a
a
c
f ( x)dx f ( x)dx;
a
b
a
2 f ( x)dx, если f x чётная ,
a
3. f ( x)dx 0
a
0, если f x нечётная ;
4. Пусть функция f(x) непрерывна на [a;b], тогда
существует по крайней
мере одна точка c a; b такая, что
b
выполнено равенство f x dx f c b a .
a
Здесь f(c) называется средним значением функции.

4.

3.2 Определённые интегралы
3.2.2 Способы вычисления определённого интеграла
1. Использование формулы Ньютона-Лейбница.
Пусть f(x) непрерывна на отрезке [a;b] и F(x) – одна из её
первообразных, тогда справедлива формула
b
b
f ( x)dx F ( x) F (b) F (a) ,
a
a
называемая формулой Ньютона-Лейбница.
Пример 1 Вычислить определённый интеграл sin xdx .
0
Решение.
sin xdx cos x 0
0
Ответ: 2.
cos cos 0 1 1 2.

5.

3.2 Определённые интегралы
3.2.2 Способы вычисления определённого интеграла
2. Использование замены переменной.
Необходимо вычислить интеграл
b
f ( x)dx
, где f(x) –
a
непрерывная функция на [a;b]. Перейдем к новой
переменной t, полагая x=φ(t). Пусть a=φ(α), b=φ(β), кроме
того, при изменении t от α до β значения функции φ(t) не
выходят за пределы отрезка [a;b]. Предположим, что
функция
φ(t)
непрерывно
дифференцируема
на
промежутке [a;b], то справедлива следующая формула
замены переменной:
b
a
f ( x)dx f ( (t )) (t )dt

6.

3.2 Определённые интегралы
3.2.2 Способы вычисления определённого интеграла
Пример 2 Вычислить определённый интеграл x 2 x 2
1
5
dx .
0
Решение.
обозначим t 2 x 2
dt 2 x 2 dx 2 xdx
1
1
5
dt
2
5 1
x
2
x
dx
xdx
t
dt
2
2
0
2
x
0
,
тогда
t
2
0
2
x 1, тогда t 2 1 1
1
1 5
1 t6
t dt
22
2 6
Ответ: 5,25.
1
2
1 6
1
63 21
6
1 2 1 64
5,25.
12
12
12 4

7.

3.2 Определённые интегралы
3.2.3 Вычисление площадей плоских фигур
в декартовой системе координат
Пусть на отрезке [a;b] задана неотрицательная
непрерывная функция y=f(x). Фигура, ограниченная сверху
графиком y=f(x), снизу – осью Оx, сбоку прямыми x=a и
y=b, называется криволинейной трапецией.
Геометрический смысл определённого интеграла:
b
S f ( x)dx ,
(1)
a
где S – площадь криволинейной трапеции.
y
y
y
y=f(x)
y=f(x)
0
S
S
y=g(x)
0
a
b
Рис. 1
x
0
a
b
x

8.

3.2.3 Вычисление площадей плоских фигур
в декартовой системе координат
Если фигура, площадь которой необходимо вычислить,
ограничена сверху графиком функции y=f(x), снизу –
графиком функции y=g(x), а сбоку прямыми x=a и x=b, то
её площадь вычисляется по формуле:
b
S f ( x) g x dx
a
y
y=f(x)
S
y=g(x)
0
a
b
Рис. 2
x
(2)

9.

3.2.3 Вычисление площадей плоских фигур
в декартовой системе координат
Частным случаем при этом является нахождение площади
фигуры, ограниченной сверху осью Оx, снизу – графиком
функции y=g(x), а сбоку прямыми x=a и x=b. В этом
случае, в формулу (2) следует подставлять f(x)=0, тогда
формула для вычисления площади такой фигуры примет
вид:
b
S g x dx
(3)
a
y
a
b
x
0
S
y=g(x)
Рис. 3

10.

3.2.3 Вычисление площадей плоских фигур
в декартовой системе координат
В некоторых случаях, чтобы вычислить площадь искомой
фигуры, необходимо разбить её на сумму или разность
двух или более криволинейных трапеций.
S S1 S 2
(4)
c
b
S1 f x dx
S 2 f x dx
a
c
y
S1
0
a
y=f(x)
c
Рис. 4
S2 b
x

11.

3.2.3 Вычисление площадей плоских фигур
в декартовой системе координат
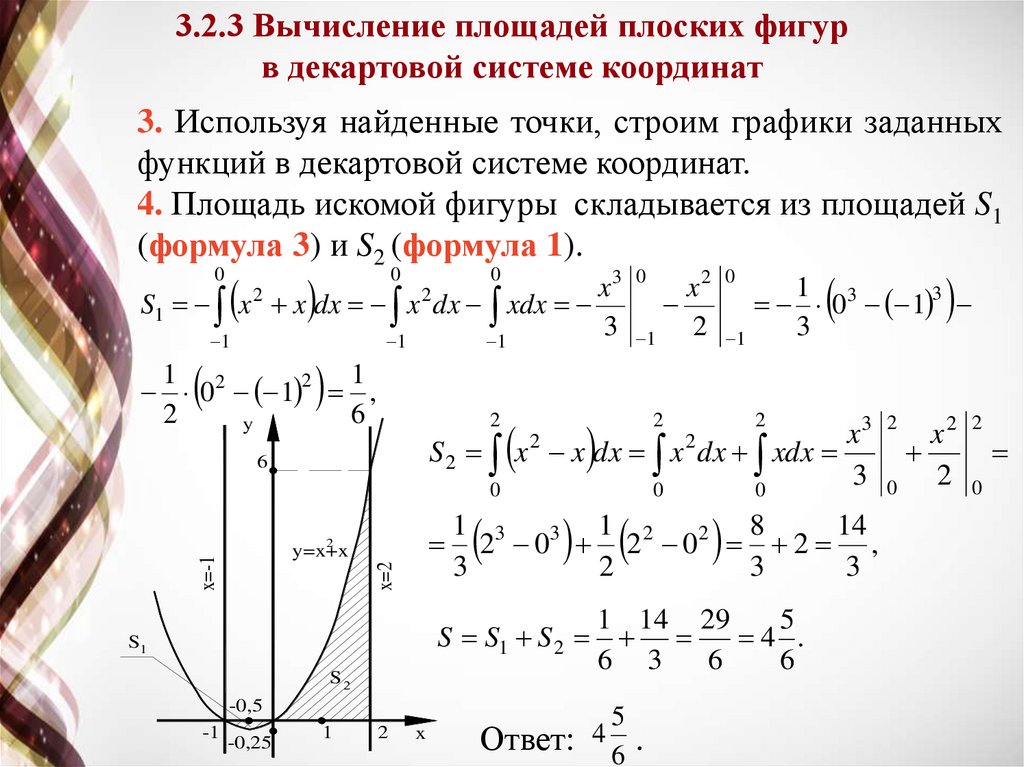
Пример 3 Вычислить площадь фигуры, ограниченной
графиками функций y=2x2, y=2.
Решение.
1. Вершиной параболы y=2x2 является точка (0;0).
2. Точки пересечения параболы и прямой находятся из
системы
x 1,
2
2
2
y 2x ,
2 x 2,
x 1,
y 2,
x 1,
y 2,
y 2,
y 2,
y 2.
Мы получили две точки (1;2) и (–1;2).

12.

П
3.2.3 Вычисление площадей плоских фигур
в декартовой системе координат
3. Используя найденные точки, строим графики заданных
функций в декартовой системе координат.
4. Сверху фигура ограничена прямой y=2, значит f(x)=2,
снизу – параболой, значит g(x)=2x2. По графику видно, что
a = –1, b = 1 (формула 2).
1 способ
b
1
1
1
1
x3
S f x g x dx 2 2 x dx 2 dx 2 x dx 2 x 2
3
1
a
1
1
1
2
1
2
1
2 3
2
4 8
2
3
2 1 1 1 1 2 2 2 4 2 .
3
3
3 3
3
y
2 способ
y=2
2
1
1
1
0
0
S 2S1 2 2 2 x dx 4 dx 4 x 2 dx
y=2x
-1
0
1
2
0
2
1
x
x3
4x 4
3
0
1
0
4 1 0
4 3
8
2
1 03 2 .
3
3
3

13.

3.2.3 Вычисление площадей плоских фигур
в декартовой системе координат
Пример 4 Вычислить площадь фигуры, ограниченной
кривой y=x2+x, прямыми x= –1, x=2 и осью Оx.
Решение.
1. Вершиной параболы является точка (–0,5;–0,25).
Замечание: координаты вершины параболы y=ax2+bx+c
(a≠0), находятся из системы
b
x0 ,
2a
y ax 2 bx c.
0
0
0

14.

3.2.3 Вычисление площадей плоских фигур
в декартовой системе координат
2. Точка пересечения параболы и прямой x = –1 находится
из системы:
x 1,
x 1,
x 1,
2
2
y 0,
y x x,
y 1 1 ,
а с прямой находится из системы:
x 2,
x 2,
x 2,
2
y 4 2,
y 6.
y x x,
Точки пересечения параболы с осью Оx (y=0) находятся из
системы:
x 0,
y x 2 x,
x 2 x 0,
x
x
1
0
,
y 0,
x 1,
y 0,
y 0,
y 0,
y 0.
Мы получили точки (–1;0), (2;6), (0;0).

15.

3.2.3 Вычисление площадей плоских фигур
в декартовой системе координат
3. Используя найденные точки, строим графики заданных
функций в декартовой системе координат.
4. Площадь искомой фигуры складывается из площадей S1
(формула 3) и S2 (формула 1).
0
0
0
3
x
S1 x 2 x dx x 2 dx xdx
3
1
1
1
1
1
0 2 1 2 ,
2
6
y
2
S2
6
0
y=x+x
2
x=2
S2
-0,25
2
1 14 29
5
4 .
6 3
6
6
-0,5
1
2
2
x
Ответ:
4
5
6
.
1
03 1 3
3
1
x3
x x dx x dx xdx
3
0
0
2
S S1 S 2
S1
-1
0
x2
2
1
1 3 3 1 2
8
14
2
2 0 2 0 2 ,
3
2
3
3
2
x=-1
0
2
x2
2
0
2
0

16.

3.2.3 Вычисление площадей плоских фигур
в декартовой системе координат
Если фигура, площадь которой необходимо вычислить,
ограничена слева осью Oy, справа – графиком функции
x=f(y), а снизу и сверху прямыми y=a, y=b соответственно,
то её площадь вычисляется по формуле:
b
S f ( y )dy
(5)
a
y
b
S
x=f(y)
a
x
0
Рис. 5

17.

3.2.3 Вычисление площадей плоских фигур
в декартовой системе координат
Если фигура, площадь которой необходимо вычислить,
ограничена слева графиком функции x=g(y), справа –
графиком функции x=f(y), а снизу и сверху прямыми y=a,
y=b соответственно, то её площадь вычисляется по
формуле:
b
S f ( y ) g y dy
(6)
a
y
b
S
x=g(y)
x=f(y)
a
x
0
Рис. 6

18.

3.2.3 Вычисление площадей плоских фигур
в декартовой системе координат
Пример 5 Вычислить площадь фигуры, ограниченной
кривой x= –2y2–1, прямой y= –1 и осями координат.
Решение.
1. Вершиной параболы является точка (–1;0).
Замечание: координаты вершины параболы x=ay2+by+c
(a≠0), находятся из системы
b
y0 ,
2a
x ax 2 bx c.
0
0
0

19.

3.2.3 Вычисление площадей плоских фигур
в декартовой системе координат
2. Точка пересечения параболы и прямой y= –1 находится
из системы:
x 2 1 2 1,
x 2 y 2 1,
x 3,
y 0,
y 1,
y 1,
с осью Оx (y=0):
x 2 y 2 1,
x 2 0 2 1,
x 1,
y 0,
y 0,
y 0,
с осью Оy (x=0):
1
2
x 2 y 2 1,
2 y 2 1 0,
y
,
2
x 0,
x 0,
y 0.
Так как последняя система не имеет решения, то точек
пересечения с осью Оy не существует.
Мы получили точки (–3;0) и (–1;0).

20.

3.2.3 Вычисление площадей плоских фигур
в декартовой системе координат
3. Используя найденные точки, строим графики заданных
функций в декартовой системе координат.
4. Слева фигура ограничена параболой, справа – осью Oy,
снизу – прямой y= –1, сверху – осью Оx.
Тогда f(y)=0, g(y)= –2y2–1, a= –1, b= 0 (формула 6).
b
S f ( y ) g y dy
a
y3
2
3
0
0 2 y
0
1
0
2
0
0
1
1
1 dy 2 y 2 dy dy
2 3
2
2
3
y 0 1 0 1 1 1 .
3
3
3
1
1
y
2
1
x=-2y-1
-3
-2
-1
0
S
-1
y=-1
1
x
Ответ: 1 2 .
3

21.

3.3 Применение интегралов в экономике
Интегральное исчисление активно используется в
экономике: степень неравенства в распределении доходов,
задача дисконтирования денежного потока, вычисление
выигрыша потребителей и выигрыша поставщиков от
установленной равновесной цены на некоторый товар и
т.п.
Предположим, что сама производственная функция f(x)
неизвестна, но известна её предельная величина f x .
Тогда при условии непрерывности справедливо равенство
f x f x dx C

22.

3.3 Применение интегралов в экономике
Пример 6 Функция предельных издержек некоторого
предприятия имеет вид С Q 60 0,04 Q 0,003 Q 2 .
Найти функцию издержек, если издержки производства
Q=100 единиц продукции составляют 7000 у.е.
Решение.
C Q С Q dQ 60 0,04 Q 0,003 Q 2 dQ 60 Q 0,02 Q 2
0,001 Q 3 A.
Постоянную A найдём из условия C(100)=7000,
тогда 60 100 0,02 1002 0,001 1003 A 7000 ,
откуда получаем A=200.
Ответ: C Q 60 Q 0,02 Q 2 0,001 Q 3 200 .

23.

3.3 Применение интегралов в экономике
Пример 7 Найти стоимость перевозки М т груза по
железной дороге на расстоянии L км при условии, что
тариф у перевозки одной тонны убывает на а рублей на
каждом последующем километре.
Решение.
Полагая, что тариф меняется непрерывно на протяжении L
километров, то есть тариф является непрерывной
функцией от l, где l 0; L , стоимость перевозки М т груза
по железной дороге на расстоянии L км можно выразить
определённым интегралом:
L
al 2 L
aL (руб.).
M y al dl M yl
ML y
2 0
2
0
aL
Ответ: ML y руб.
2

24.

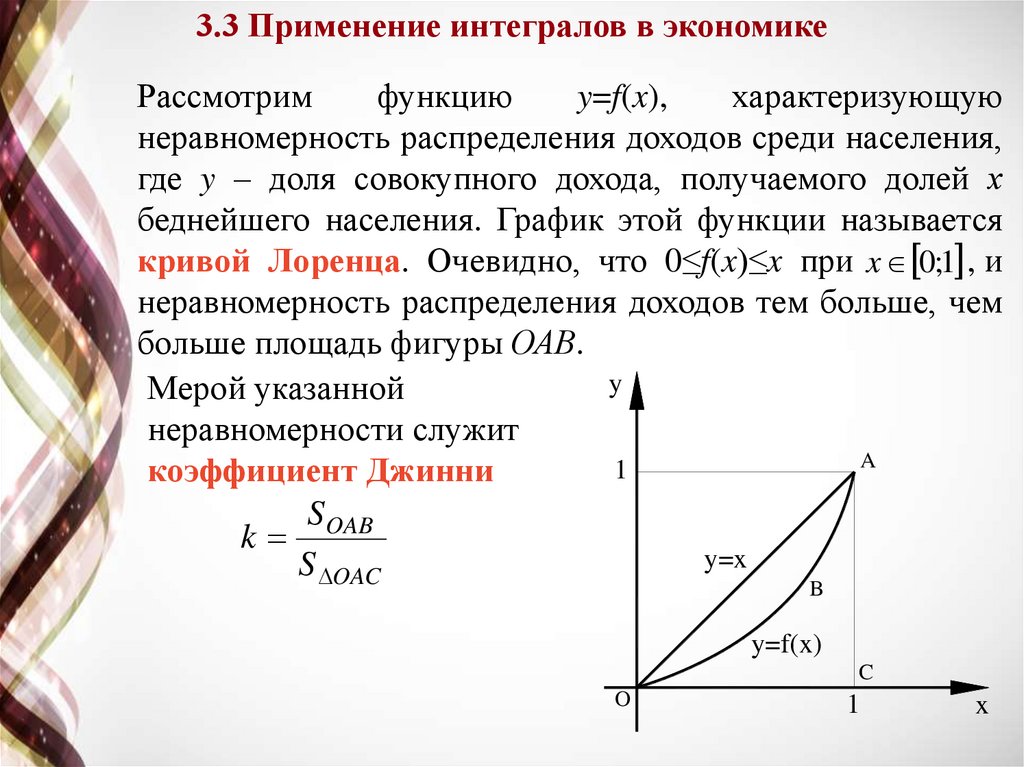
3.3 Применение интегралов в экономике
Рассмотрим
функцию
y=f(x),
характеризующую
неравномерность распределения доходов среди населения,
где y – доля совокупного дохода, получаемого долей х
беднейшего населения. График этой функции называется
кривой Лоренца. Очевидно, что 0≤f(x)≤x при x 0;1 , и
неравномерность распределения доходов тем больше, чем
больше площадь фигуры ОАВ.
y
Мерой указанной
неравномерности служит
A
1
коэффициент Джинни
S OAB
k
y=x
S OAC
B
y=f(x)
C
O
1
x

25.

3.3 Применение интегралов в экономике
Пример 8 По данным исследований в распределении
доходов одной из стран, кривая Лоренца может быть
3
5
, где x – доля населения,
описана уравнением y
2 x 3
y – доля доходов населения. Вычислить коэффициент
Джинни, оценить распределение доходов 40% наиболее
низко оплачиваемого населения.
Решение.
1
SOAB
3
5
x2
5
x
dx
3 ln 2 x x
2 x 3
2
3
0
13
3 ln 2 0,087.
6
1
0
1
5
3 ln 2
2
3
y
A
1
y=x
B
y=f(x)
C
O
1
x

26.

3.3 Применение интегралов в экономике
Вычислим коэффициент Джинни:
k
SOAB 0,087
0,174.
S OAC
0,5
3
5 5
y 0,4
0,21,
2 0,4 3 24
это означает, что 40% наиболее низко оплачиваемого
населения получает 21% совокупного национального
дохода.
Следует также отметить, что y 0,2
3
5
0,
2 0,2 3
получается, что 20% населения не получают ничего.
Ответ: k=0,174; y(0,4)=0,21.