Интегральное исчисление функций одной переменной. Определенный интеграл

1.

Лекция 25
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ
ОДНОЙ ПЕРЕМЕННОЙ
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ(3)

2.

Квадратурная формула Симпсона (формула парабол)
Оценка определенных интегралов
Вычисление площадей плоских фигур
Площадь в полярных координатах

3.

Квадратурная формула Симпсона (формула парабол).
Томас Симпсон (1710-1761)- английский
математик)
В диссертации 1743 озаглавленной «Of the areas
of curves etc. by approximation» (стр. 109—119),
вывел известную под названием правила
Симпсона формулу приближённого определения
квадратур

4.

Разделим отрезок интегрирования [a, b] на четное число отрезков (2m).
Площадь криволинейной трапеции, ограниченной графиком функции f(x)
на каждой паре отрезков заменим на площадь криволинейной трапеции,
ограниченной параболой второй степени с осью симметрии,
параллельной оси Оу и проходящей через точки кривой, со значениями
f(x0), f(x1), f(x2).
0 х0
х1
х2
х3
х4
х

5.

Уравнения этих парабол имеют вид Ax2 + Bx + C, где
коэффициенты А, В, С могут быть легко найдены по трем точкам
пересечения параболы с исходной кривой.
y 0 Ax 02 Bx 0 C
y1 Ax12 Bx1 C
y 2 Ax 22 Bx 2 C
Обозначим 2h x 2 x 0 .
x2
x3
x2
x2
S ( Ax Bx C ) dx A B
Cx
3
2
x0
x0
2

6.

h
3
Если принять х0 = -h, x1 = 0, x2 = h, то S ( 2 Ah 2 6C )
Тогда система уравнения примет вид:
y 0 Ah 2 Bh C
y1 C
y 2 Ah 2 Bh C
C учетом этого:
y 0 4 y1 y 2 2 Ah 2 6C

7.

Отсюда
h
S ( y 0 4 y1 y 2 )
3
Можно записать общее выражение
x2
x0
h
f ( x)dx ( y0 4 y1 y2 )
3
x4
x2
f ( x)dx
h
( y2 4 y3 y4 )
3
...............................................

8.

Складывая эти выражения, получаем формулу Симпсона:
b
a
f ( x)dx
b a
y 0 y 2 m 2( y 2 y 4 ... y 2 m 2 ) 4( y1 y3 ... y 2m 1 )
6m
Чем больше взять число m, тем более точное значение интеграла будет
получено.

9.

Оценим ошибку формулы Симпсона, то есть величину
Предположим, что функция f(x) имеет на отрезке [a;b] непрерывную
четвёртую производную , причём
при всех
Тогда при выборе постоянного шага
имеет место неравенство

10.

Таким образом, формула Симпсона -- это квадратурная формула
четвёртого порядка точности. Это означает, что при уменьшении шага
h вдвое ошибка уменьшится примерно в 16 раз, а при уменьшении шага
в 10 раз ошибка уменьшится примерно в 10000 раз.

11.

Пример.
Вычислить приближенное значение определенного интеграла
8
x 3 16dx
2
с помощью формулы Симпсона, разбив отрезок интегрирования
на 10 частей.
По формуле Симпсона получим:
8
2
x3 16dx
8 2
[ y ( 2) y (8) 2[ y (0) y (2) y (4) y (6)]
6 5
4[ y ( 1) y (1) y (3) y (5) y (7)]].

12.

8
2
x 3 16dx
8 2
[2.828 22.978 2[4 4.899 8.944 15.232]
6 5
4[3.873 4.123 6.557 1.874 18.947]] 91.151
Точное значение этого интеграла – 91.173.
Как видно, даже при сравнительно большом шаге разбиения точность
полученного результата вполне удовлетворительная

13.

Для сравнения применим к этой же задаче формулу
трапеций.
8
2
x 3 16dx
b a y0 yn
y
y
...
y
1
2
n 1
n 2
8 2 2.828 22.978
3.873 4 4.123
10
2
4.899 6.557 8.944 11.874 15.232 18.947) 91.352

14.

Кроме вышеперечисленных способов, можно вычислить значение
определенного интеграла с помощью разложения подинтегральной
функции в степенной ряд.
Принцип этого метода состоит в том, чтобы заменить
подинтегральную функцию по формуле Тейлора и почленно
проинтегрировать полученную сумму.

15.

16.

Оценка определенных интегралов
Имеют место более общие теоремы об оценке и среднем: если
функции f(x) и φ(x) непрерывны на отрезке [a, b] и φ(x) > 0, m наименьшее, M - наибольшее значения функции f(x), то
неравенство Коши-Буняковского

17.

Пример 1. Оценить определённый интеграл

18.

Вычисление площадей плоских фигур
1. Пусть функция y f(x) непрерывна и неотрицательна на
отрезке [a;b] .
Тогда по геометрическому смыслу определенного интеграла
площадь S под кривой (площадь криволинейной трапеции)
численно равна определенному интегралу
b
f(x)dx
a

19.

Пример
Найти площадь фигуры, ограниченной параболой y x 2 , прямыми
x 0 , x 1 и осью ОХ.
Решение.
1
x3
2
S x dx
3
0
1
0
1
.
3

20.

2. Пусть функция y f(x) непрерывна и неположительна на отрезке
[a; b] .
Отразим функцию y f(x) относительно оси ОХ, получим функцию
y f ( x ) , расположенную над осью ОХ.
Площадь
под
кривой
y f ( x ) будет равна
b
b
S - f(x) dx - f(x)dx
a
a
b
Следовательно, величина найденного интеграла
f(x)dx
a
знаком от величины площади S.
будет отличаться

21.

ПРИМЕР 2. Найти площадь фигуры, ограниченной параболой
y x 2 , прямыми x 0 , x 1 и осью ОХ.
1
Решение.
x3
2
S x dx
3
0
1
0
1
3

22.

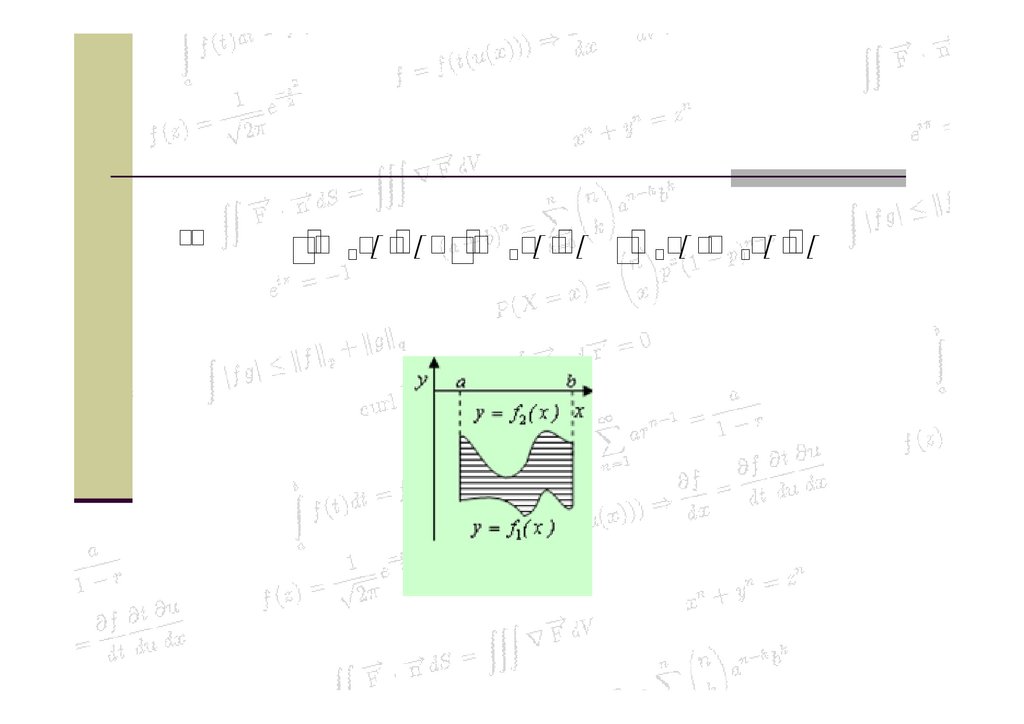
3. Пусть функции y f1(x) и y f 2 ( x ) непрерывны на
отрезке [a;b] , причем f 2 ( x ) f1 ( x )
Тогда площадь фигуры, ограниченная кривыми y f1(x) и
y f 2 ( x ) , будет равна разности площадей криволинейных
трапеций, ограниченных этими линиями:
b
S
f
a
2(
x ) f1 ( x ) dx

23.

а)
b
S
f
a
b
2(
x )dx
b
f ( x )dx f
1
a
a
2(
x ) f1 ( x ) dx

24.

b
б)
S
b
f ( x ) dx f
1
a
a
b
2(
x ) dx
f
a
2(
x ) f1 ( x ) dx

25.

b
в)
b
b
S f 2 ( x)dx f1 ( x) dx f 2 ( x) f1 ( x) dx
a
a
a

26.

г) Площадь на последнем рисунке может быть вычислена, как сумма
площадей криволинейных трапеций видов, изображенных на рис. а-в,
и, следовательно, по той же формуле.

27.

Пример
Найти площадь фигуры, ограниченной
линиями
y 2 x2
y x
Решение. Найдем точки пересечения графиков заданных
функций: 2 x 2 x , откуда x1 1, x2 2 .
2
Искомая площадь
2
x3 x2
2
S 2 x ( x ) dx 2 x
4 ,5
3
2
1
1

28.

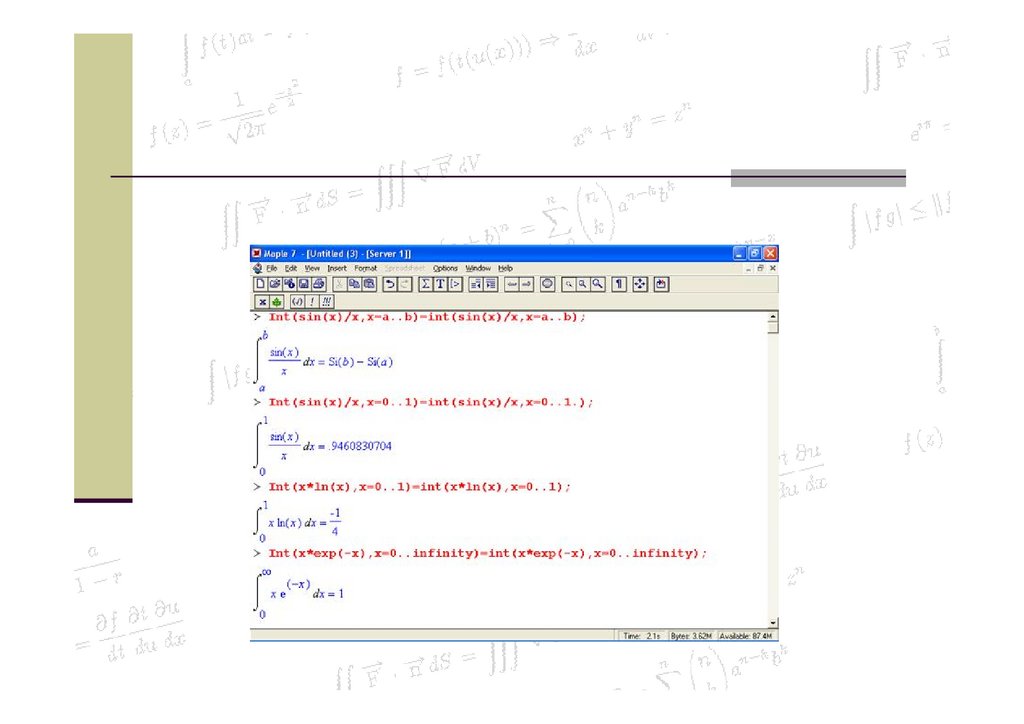
Вычисления в Maple
Площадь фигуры, ограниченной функцией f ( x ), пересекающей ось
абсцисс, определяется формулой
где xi – нули функции.

29.

Другими словами, чтобы вычислить площадь
этой фигуры, нужно разбить отрезок [ a ; b ] нулями функции f ( x )
на части, проинтегрировать функцию f по каждому из получившихся
промежутков знакопостоянства, сложить отдельно интегралы по отрезкам,
на которых функция f принимает разные знаки, и вычесть из первого
второе.

30.

Площадь в полярных координатах
Напомним, что определением интеграла служит предел интегральных
сумм, взятый при условии измельчения разбиения отрезка
интегрирования.
Этим определением мы воспользуемся для нахождения площади в
следующем случае.
Пусть на плоскости фиксирована система полярных координат:
полярными координатами точки М служат два числа
- полярный радиус,
- полярный угол.

31.

Уравнение, задающее зависимость величины τ от полярного угла φ
задаёт некоторую линию на плоскости.
Будем предполагать, что функция
непрерывна при

32.

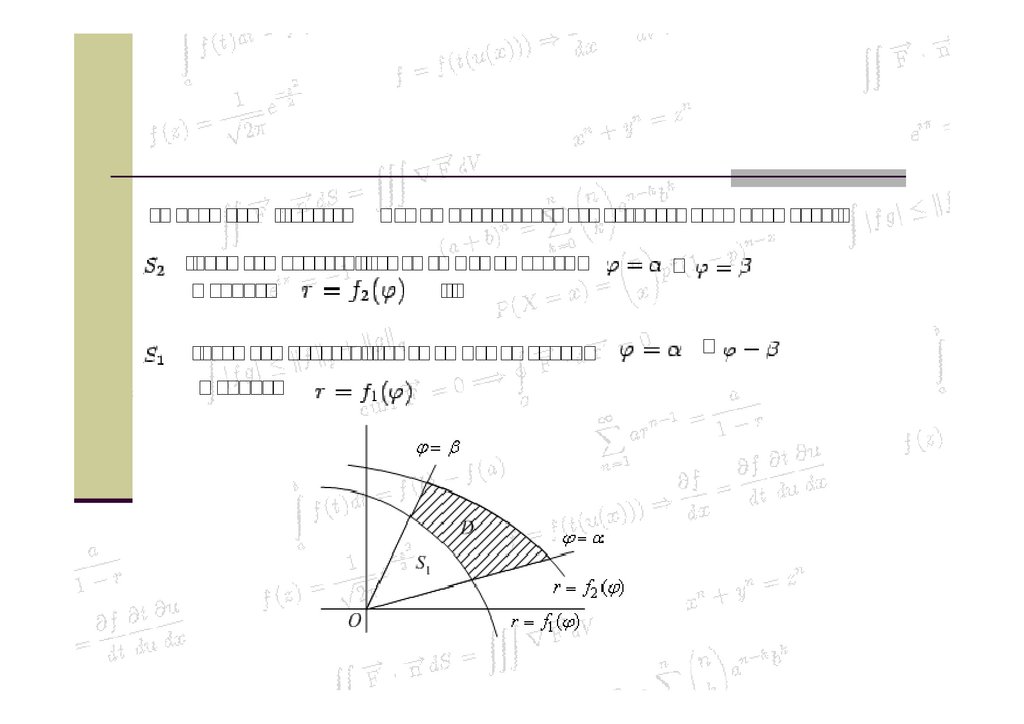
Рассмотрим область D на плоскости, расположенную
между выходящими из начала координат лучами
и
и линией

33.

Найдём площадь области D, вначале приблизив область ступенчатой
фигурой следующего устройства.
Область изменения угла φ, то есть отрезок [α; β], разобьём на части
точками деления
и выберем на каждом участке
некоторую отмеченную точку
Получаем размеченное разбиение отрезка [α; β].

34.

Приближённо будем считать площадь
лучами
и
с тем же центральным углом
сектора области D, лежащего между
, равной площади
кругового сектора
и радиусом, равным

35.

Площадь кругового сектора подсчитывается по формуле
Значит, площадь всей области приближённо равна интегральной сумме
построенной по выбранному размеченному разбиению отрезка [α; β] для функции

36.

При неограниченном измельчении разбиения
эта интегральная сумма будет стремиться к площади области D.
С другой стороны, предел интегральных сумм для функции
даст определённый интеграл от этой функции.
Таким образом, получаем формулу площади:

37.

Более кратко эту формулу можно записать так:
где имеется в виду, что вместо полярного радиуса нужно подставить
его выражение через полярный угол φ для зависимости, график которой
ограничивает область снаружи

38.

Вычислить площадь фигуры, ограниченной линией
угол, как и в примере с площадью круга, принимает все значения
от
до

39.

40.

Пример.
Найдём площадь S области, ограниченной частью спирали
(
)
при
Применяя формулу
получаем:
и отрезком
оси Ох

41.

Если область D имеет границу, состоящую из двух отрезков лучей
и
(эти отрезки могут вырождаться в одну точку)
и двумя линиями, заданными уравнениями в полярных координатах:
и
, причём
при всех

42.

то площадь S области D можно представить как разность двух площадей:
-площади области, лежащей между лучами
и линией
,и
-площади области, лежащей между лучами
и линией
,
,

43.

Каждую из площадей S1 и S2 можно подсчитать по формуле
Таким образом,

44.

Вычислить площадь фигуры, ограниченной линиями
в полярных координатах

45.

46.

47.

Вычисление объемов тел.
Вычисление объема тела по известным площадям его
параллельных сечений
Пусть имеется тело объема V.
Площадь любого поперечного
сечения тела Q, известна как
непрерывная функция Q =
Q(x).
Q(xi-1)
Q(xi)
a
xi-1
xi
b
Разобьем тело на “слои” поперечными сечениями, проходящими через точки хi
разбиения отрезка [a, b].
Т.к. на каком- либо промежуточном отрезке разбиения [xi-1, xi] функция Q(x)
непрерывна, то принимает на нем наибольшее и наименьшее значения.
Обозначим их соответственно Mi и mi.
x

48.

Если на этих наибольшем и наименьшем сечениях построить цилиндры с
образующими, параллельными оси х, то объемы этих цилиндров будут
соответственно равны Mi xi и mi xi здесь xi = xi - xi-1.
Произведя такие построения для всех отрезков разбиения, получим цилиндры,
n
объемы которых равны соответственно
M x
i
i
и
m x
i
i
i 1
При стремлении к нулю шага разбиения , эти суммы имеют общий предел:

49.

Таким образом, объем тела может быть найден по формуле:
Недостатком этой формулы является то, что для нахождения объема
необходимо знать функцию Q(x), что весьма проблематично для
сложных тел.

50.

Пример: Найти объем шара радиуса R.
y
В поперечных сечениях шара получаются окружности
переменного радиуса у.
-R
В зависимости от текущей координаты х этот
радиус выражается по формуле
.
Тогда функция площадей сечений имеет вид: Q(x) =
Получаем объем шара:
R
0
y
x
R
x

51.

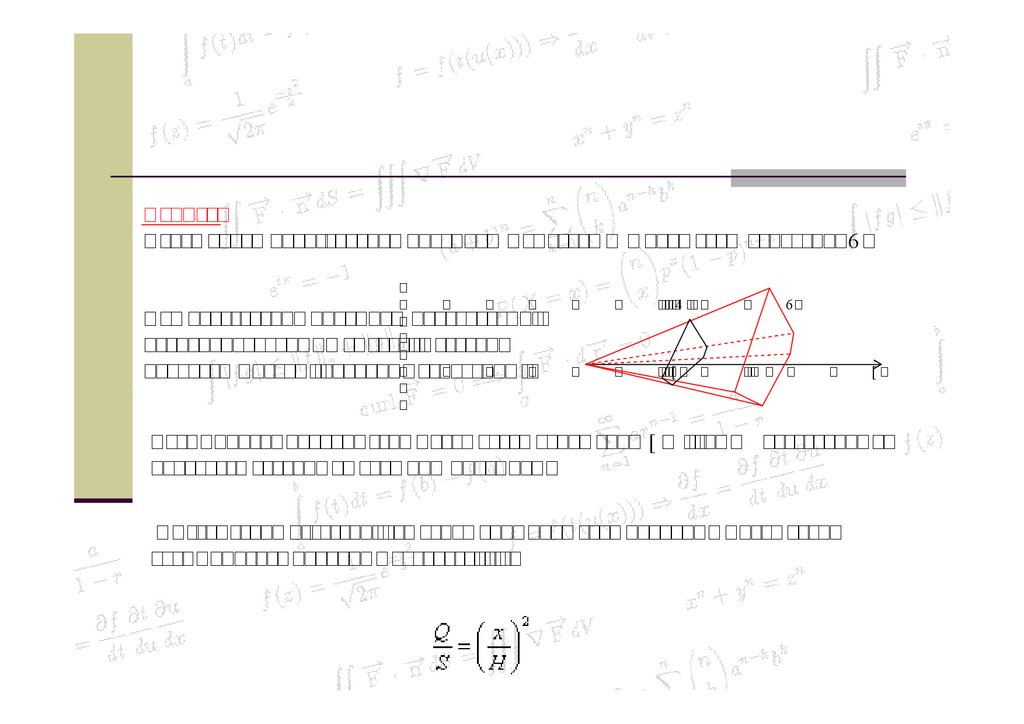
Пример:
Найти объем произвольной пирамиды с высотой Н и площадью основания S.
При пересечении пирамиды плоскостями,
перпендикулярными высоте, в сечении
получаем фигуры, подобные основанию.
Q
x
S
H
x
Коэффициент подобия этих фигур равен отношению x/H, где х – расстояние от
плоскости сечения до вершины пирамиды.
Из геометрии известно, что отношение площадей подобных фигур равно
коэффициенту подобия в квадрате, т.е.

52.

Отсюда получаем функцию площадей сечений:
Находим объем пирамиды:

53.

ОБЪЕМ ТЕЛ ВРАЩЕНИЯ
Рассмотрим кривую, заданную уравнением y = f(x).
Предположим, что функция f(x) непрерывна на отрезке [a, b].
Если соответствующую ей криволинейную трапецию с основаниями а и b
вращать вокруг оси Ох, то получим так называемое тело вращения.
Т.к. каждое сечение тела плоскостью x = const
представляет собой круг радиуса
,
то объем тела вращения может быть легко найден
по полученной выше формуле:
y = f(x)

54.

ПЛОЩАДЬ ПОВЕРХНОСТИ ТЕЛА ВРАЩЕНИЯ
Мi
Определение: Площадью поверхности вращения
кривой АВ вокруг данной оси называют предел, к
которому стремятся площади поверхностей вращения
ломаных, вписанных в кривую АВ, при стремлении к
нулю наибольших из длин звеньев этих ломаных
B
А
х
xi
Разобьем дугу АВ на n частей точками M0, M1, M2, … , Mn.
Координаты вершин полученной ломаной имеют координаты xi и yi.

55.

При вращении ломаной вокруг оси получим поверхность, состоящую из
боковых поверхностей усеченных конусов, площадь которых равна DPi.
Эта площадь может быть найдена по формуле:
Здесь Si – длина каждой хорды.

56.

Применяем теорему Лагранжа к отношению
Получаем:
Тогда

57.

Площадь поверхности, описанной ломаной равна:
Эта сумма не является интегральной, но можно показать, что

58.

Тогда
- формула вычисления площади поверхности тела вращения.