Похожие презентации:
Теорема Остроградского – Гаусса
1.
§5 Теорема Остроградского – ГауссаГлава 3
Электричество и магнетизм
2.
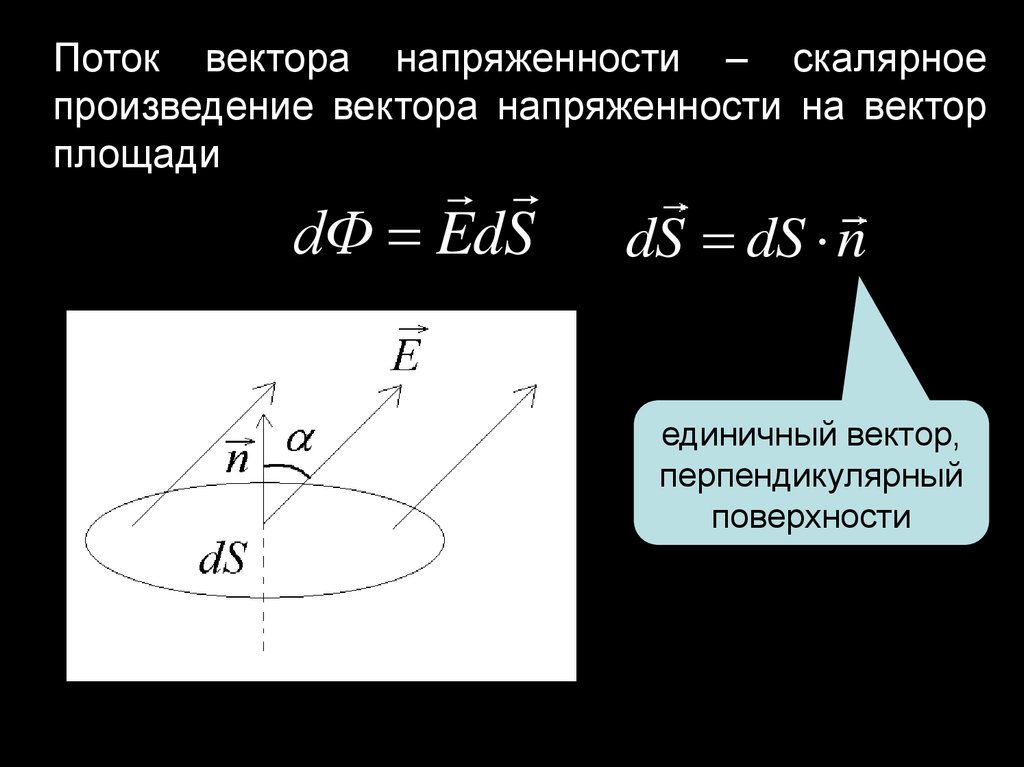
Поток вектора напряженности – скалярноепроизведение вектора напряженности на вектор
площади
dФ EdS
dS dS n
единичный вектор,
перпендикулярный
поверхности
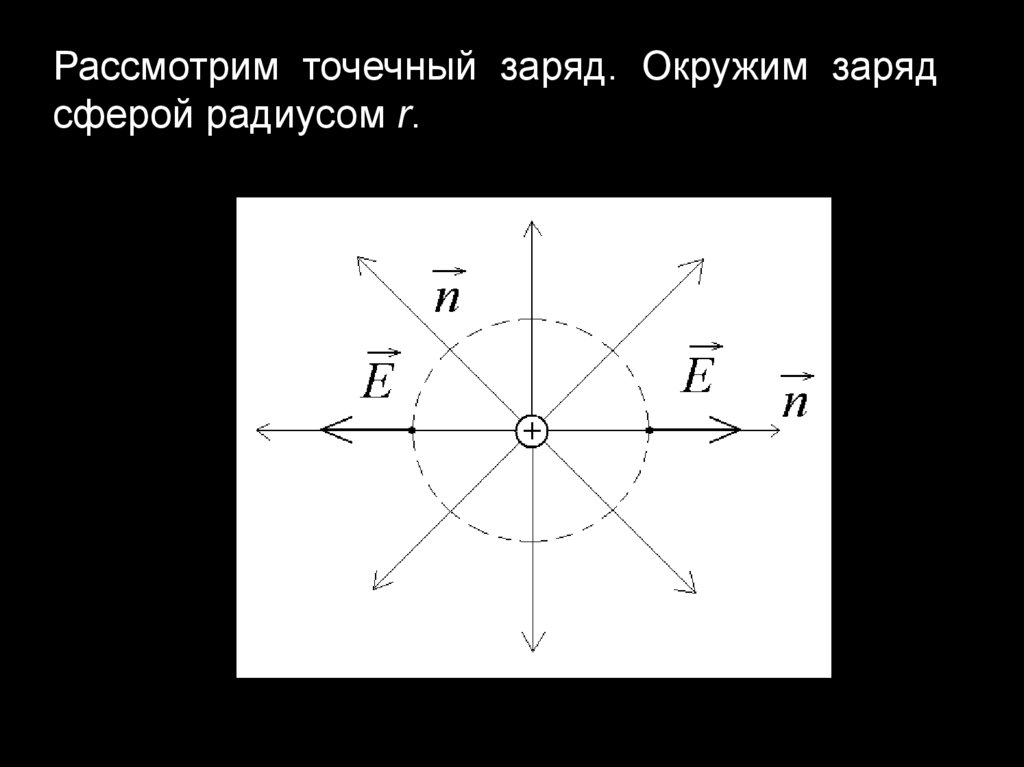
3.
Рассмотрим точечный заряд. Окружим зарядсферой радиусом r.
4.
Поток вектора напряженности сквозь поверхностьсферы равен
q
Ô EdS k 3 rndS
r
S
S
kq
2
r
kq
q
2
dS
4
r
2
S
r
0
5.
Таким образом, суммарный поток сквозьзамкнутую поверхность определяется зарядом,
охватываемым замкнутой поверхностью.
Ф
q
0
6.
Если поверхность охватывает множествозарядов, то согласно принципу суперпозиции:
n
E Ei
i 1
7.
Суммарныйпоток
сквозь
замкнутую
поверхность
определяется
зарядами,
охватываемыми замкнутой поверхностью.
n
n
EdS E dS E dS
i
S i 1
S
n
i 1
qi
0
1
0
i 1 S
n
q
i 1
i
i
8.
Теорема Гаусса в интегральной форме:S
q
EdS
i
0
поток вектора напряженности электрического
поля сквозь замкнутую поверхность равен
алгебраической сумме зарядов охватываемых
этой поверхностью, делённой на 0.
9.
Поскольку суммарный заряд может бытьнайден интегрированием по объему
q dV
i
V
то теорема Гаусса принимает вид:
EdS
S
1
dV
0 V
10.
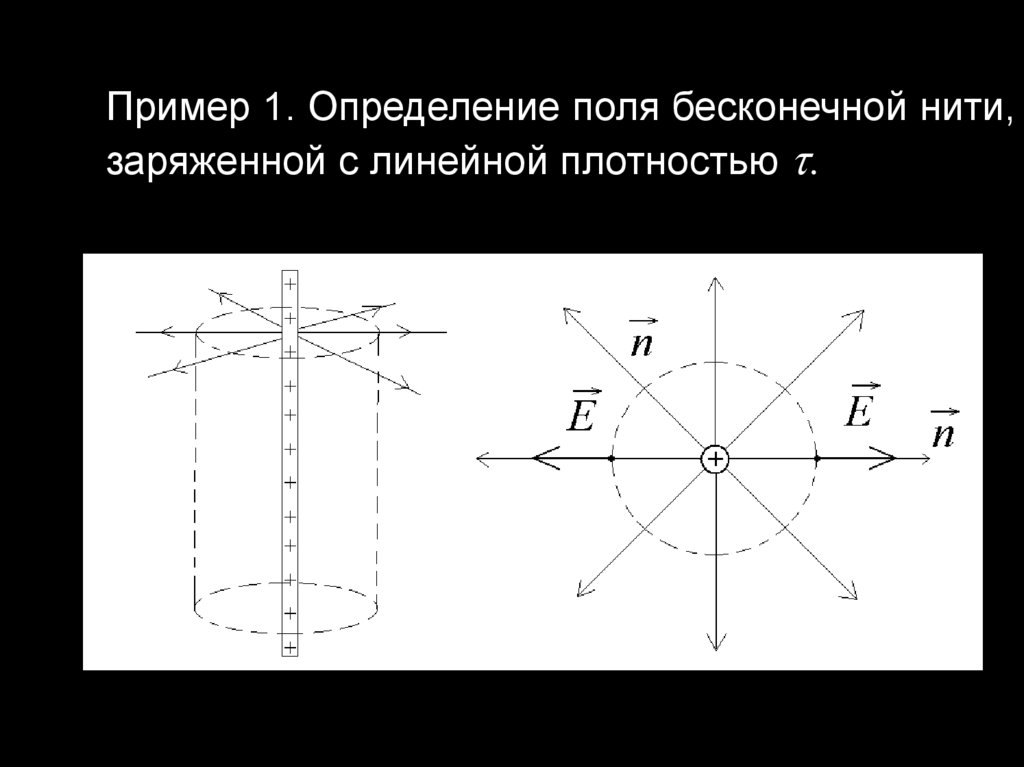
Пример 1. Определение поля бесконечной нити,заряженной с линейной плотностью .
11.
В качестве поверхности выберем поверхностьцилиндра.
Поток
через
поверхность,
определяется только потоком через боковую
поверхность:
EdS E 2 rl
S
q
0
i
1
0
l
E
2 0 r
12.
Пример 2. Найти напряженностьконцентрических заряженных сфер.
поля
двух
R1 R
R2 2 R
1
2
E (r ) ?
13.
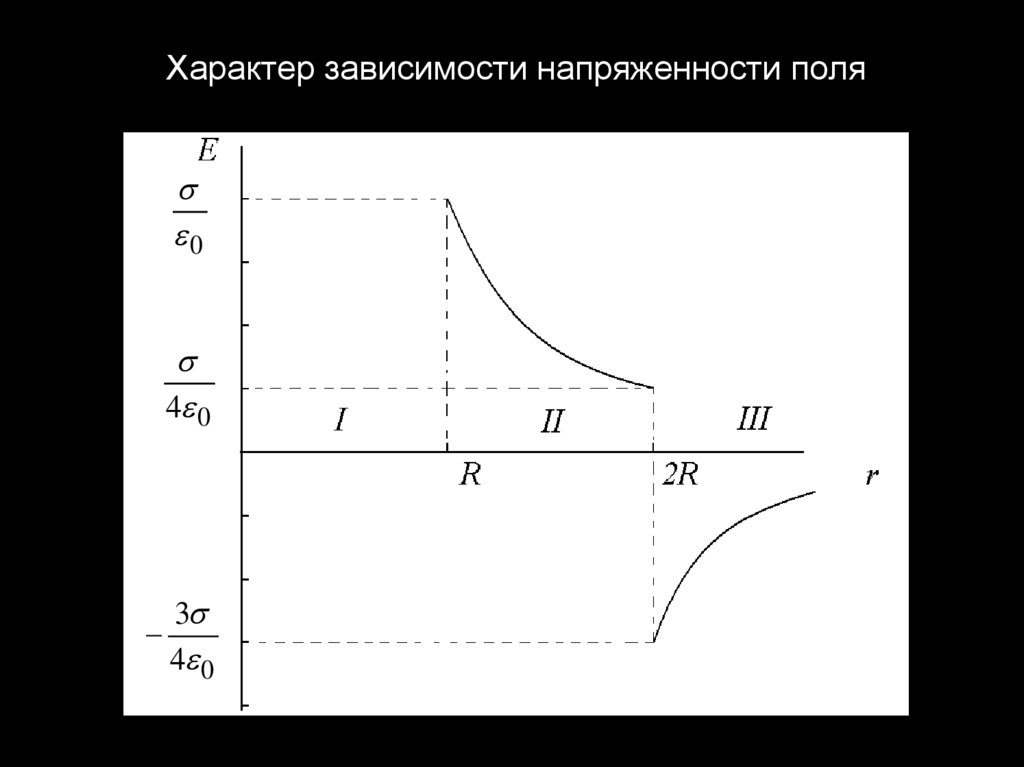
Поле двух концентрических сфер в трех областях.I . EI = 0
II . E 4 r
2
1
0
R
E
0r 2
2
EII ( R )
0
EII ( 2 R )
4 0
4 R
2
14.
III . E 4 r2
1
0
( 4 R 4 ( 2 R ) )
2
3 R
E
2
0r
2
3
E III (2 R)
4 0
2
15.
Характер зависимости напряженности поля0
4 0
3
4 0
16.
Пример 3. Рассмотрим поле двух коаксиальныхцилиндров.
1
2
R1 R
R2 2 R
E (r ) ?
17.
I . EI 02 Rh
II . EII 2 rh
0
R
EII
0r
E II ( R)
0
E II (2 R)
2 0
18.
2 Rh ( )2 2 Rh 2 RhIII . EIII 2 rh
0
0
R
E III
0r
E III (2 R)
2 0










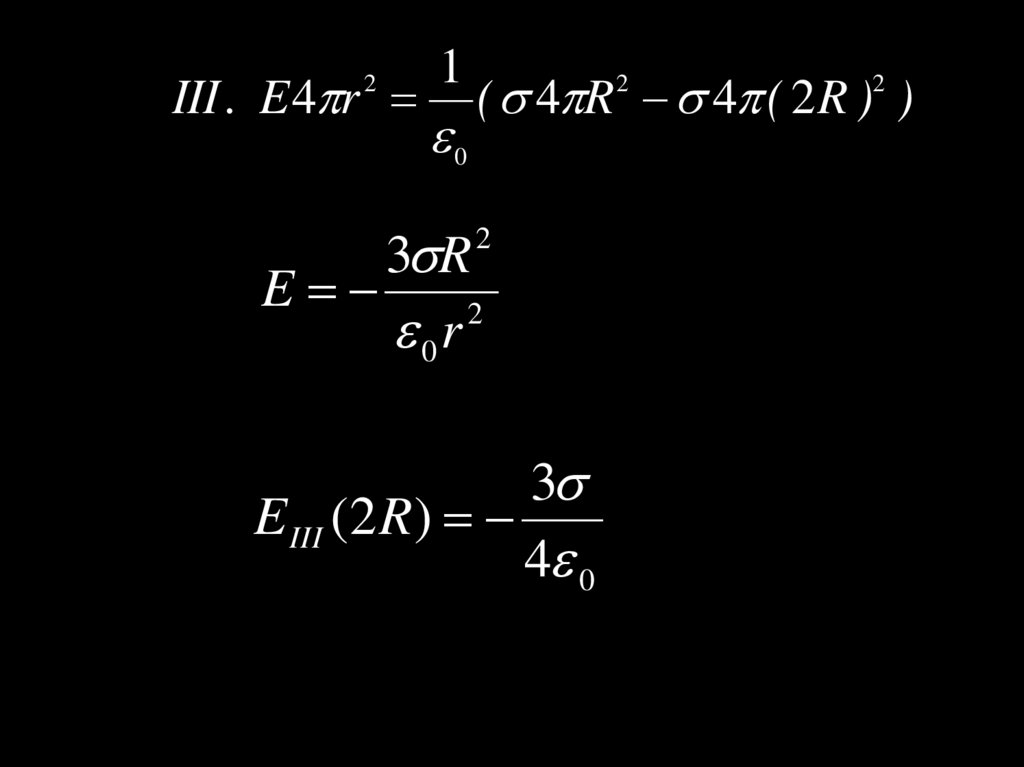

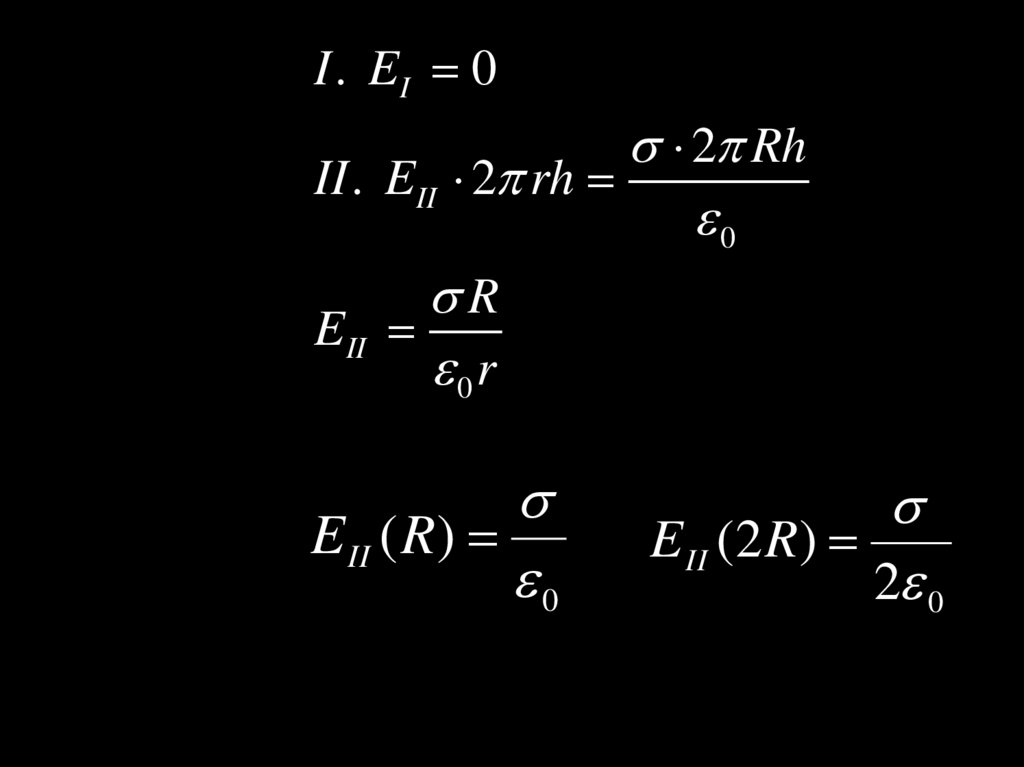

 Физика
Физика








