Проецирование. Виды проецирования

1. ЛЕКЦИЯ 2

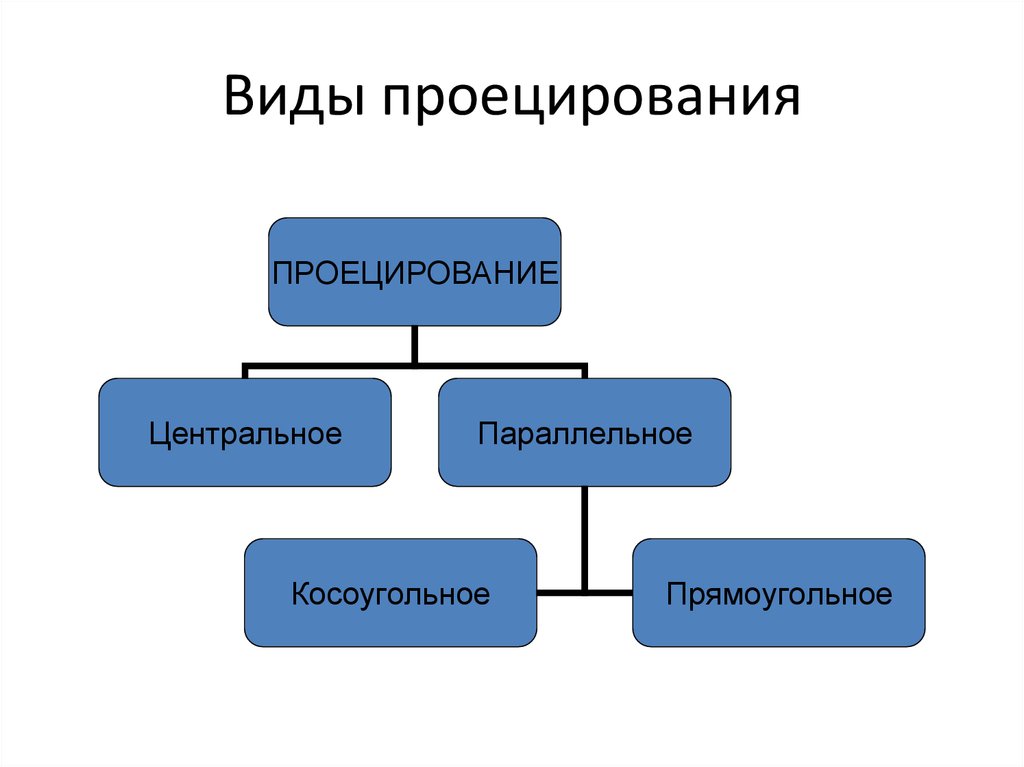
ПРОЕЦИРОВАНИЕ

2. Виды проецирования

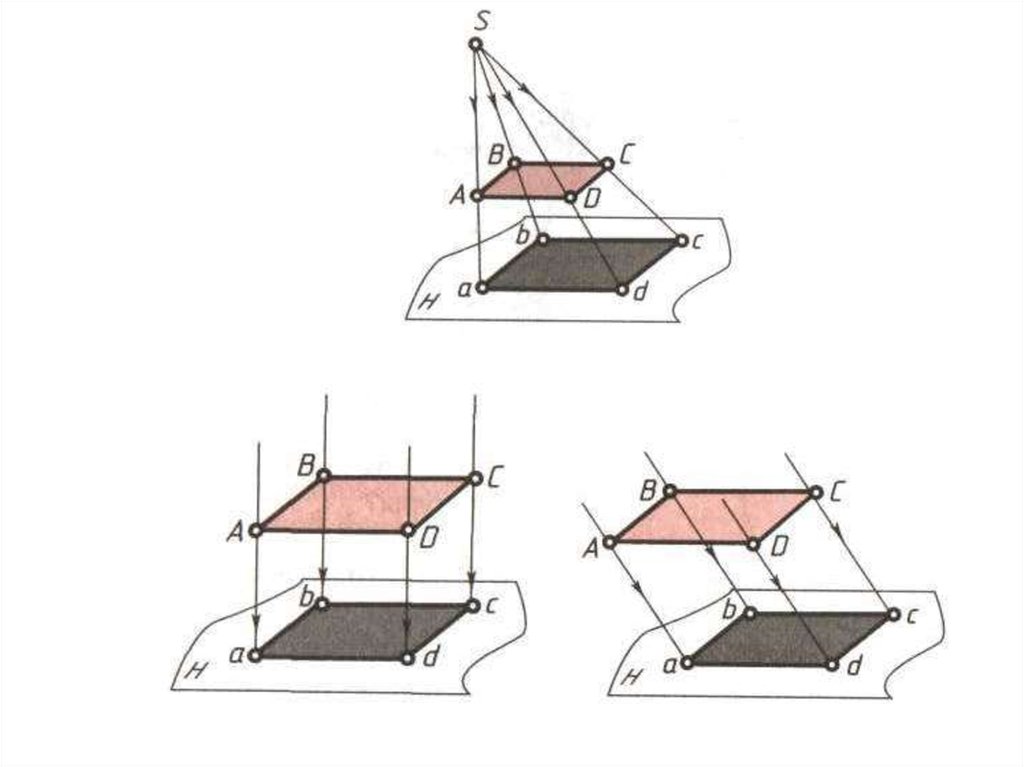
ПРОЕЦИРОВАНИЕ
Центральное
Параллельное
Косоугольное
Прямоугольное

3.

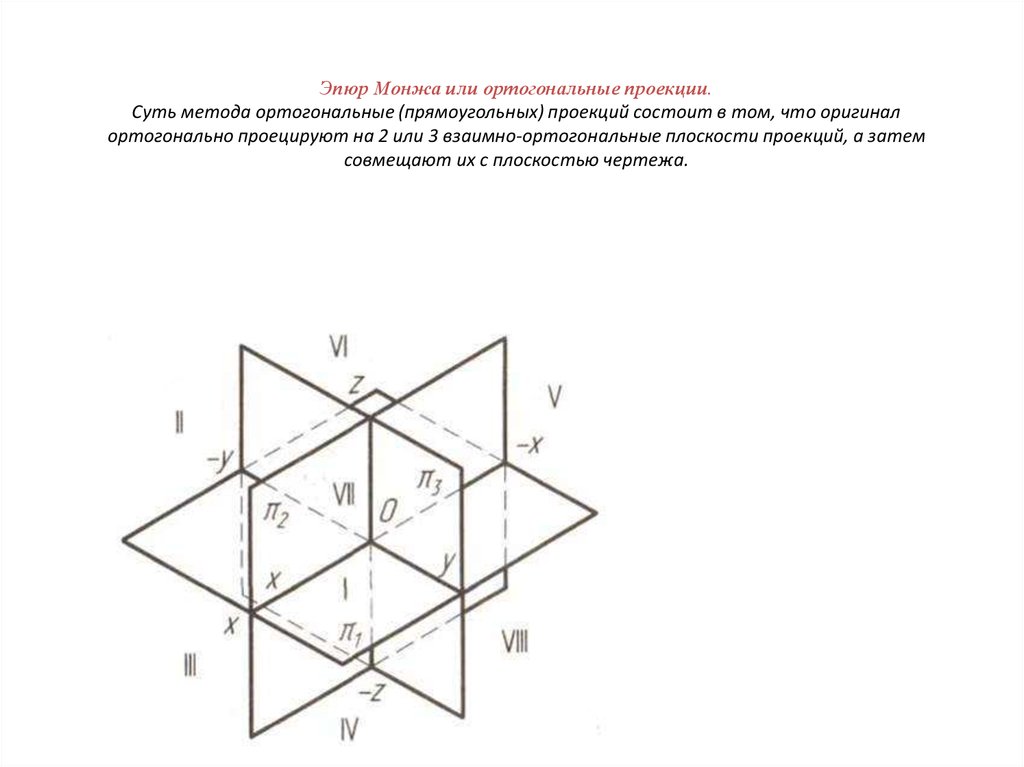
4. Эпюр Монжа или ортогональные проекции. Суть метода ортогональные (прямоугольных) проекций состоит в том, что оригинал

ортогонально проецируют на 2 или 3 взаимно-ортогональные плоскости проекций, а затем
совмещают их с плоскостью чертежа.

5. Проекции точки, линии, плоскости

6.

7.

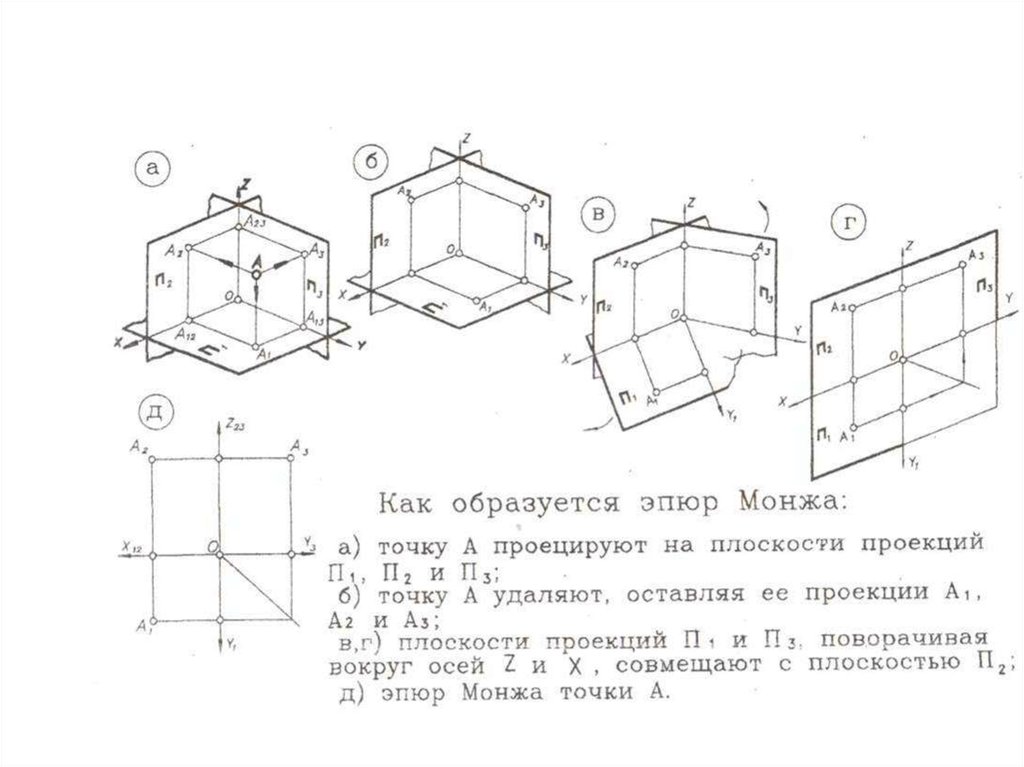
Полученный чертеж является трёхпроекционным ортогональным
чертежом точки А.
На чертеже линии связи А2 А1 и А2 А3 перпендикулярны к
соответствующим осям. По ортогональному чертежу можно судить о
расстоянии от точки А до плоскостей П1, П2 и П3.

8.

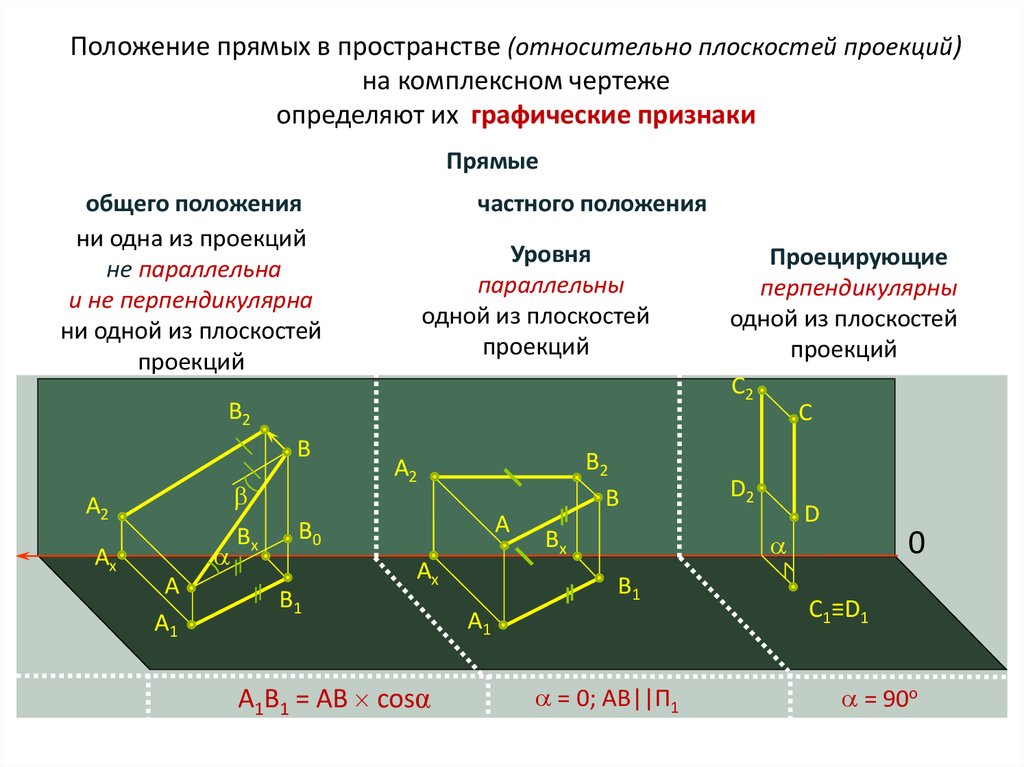
Положение прямых в пространстве (относительно плоскостей проекций)
на комплексном чертеже
определяют их графические признаки
Прямые
общего положения
ни одна из проекций
не параллельна
и не перпендикулярна
ни одной из плоскостей
проекций
частного положения
Уровня
параллельны
одной из плоскостей
проекций
B2
B
A2
Ax
A
A1
Вx
B2
B
A2
A
B0
B1
Ax
А1В1 = АВ cosα
Вx
Проецирующие
перпендикулярны
одной из плоскостей
проекций
C2
C
D2
D
0
B1
A1
= 0; АВ||П1
C1≡D1
= 90o

9.

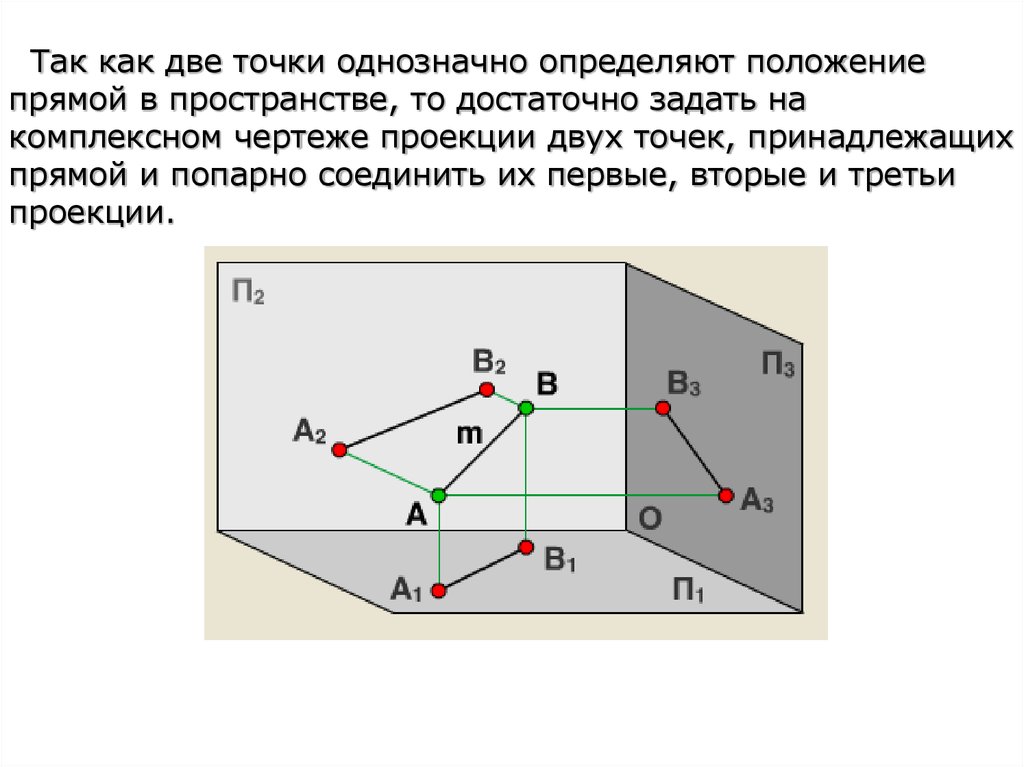
Так как две точки однозначно определяют положение
прямой в пространстве, то достаточно задать на
комплексном чертеже проекции двух точек, принадлежащих
прямой и попарно соединить их первые, вторые и третьи
проекции.

10.

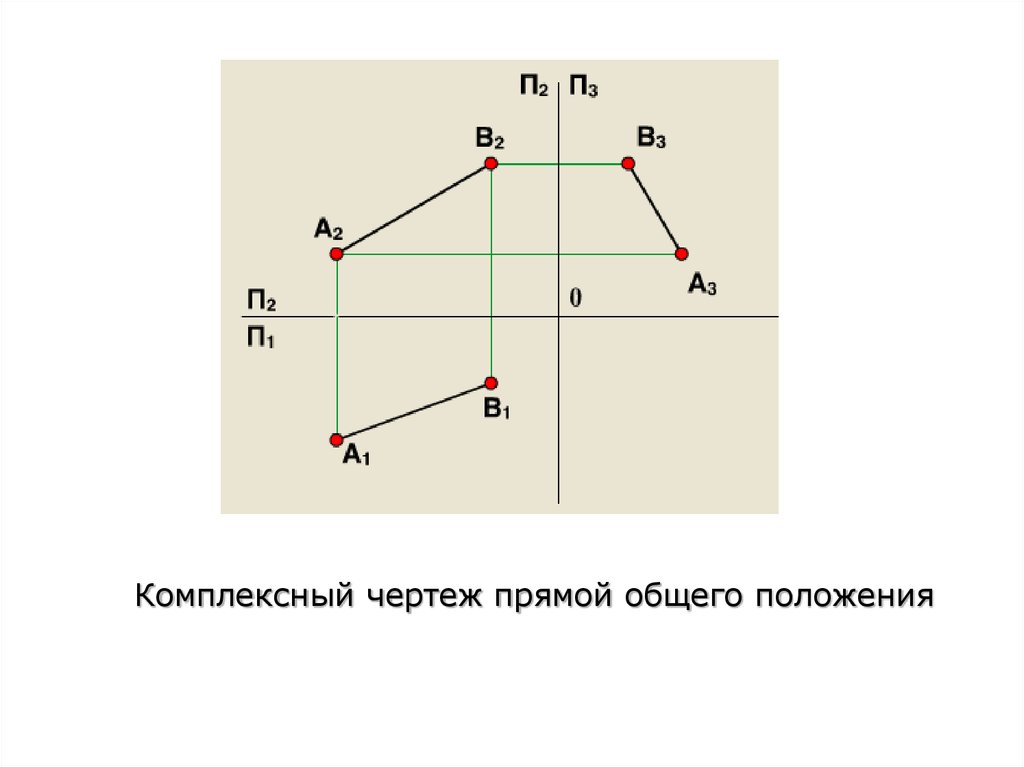
Комплексный чертеж прямой общего положения

11.

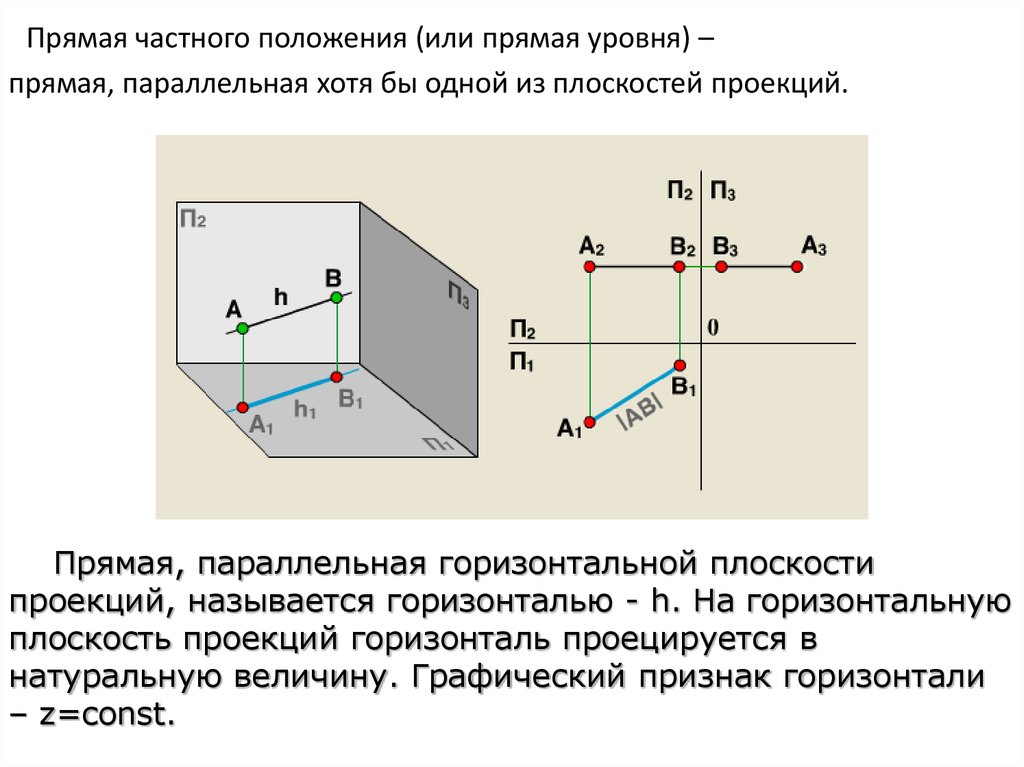
Прямая частного положения (или прямая уровня) –
прямая, параллельная хотя бы одной из плоскостей проекций.
Прямая, параллельная горизонтальной плоскости
проекций, называется горизонталью - h. На горизонтальную
плоскость проекций горизонталь проецируется в
натуральную величину. Графический признак горизонтали
– z=const.

12.

Прямая, параллельная фронтальной плоскости проекций,
называется фронталью - f. На фронтальную плоскость
проекций фронталь проецируется в натуральную величину.
Графический признак фронтали – y=const.

13.

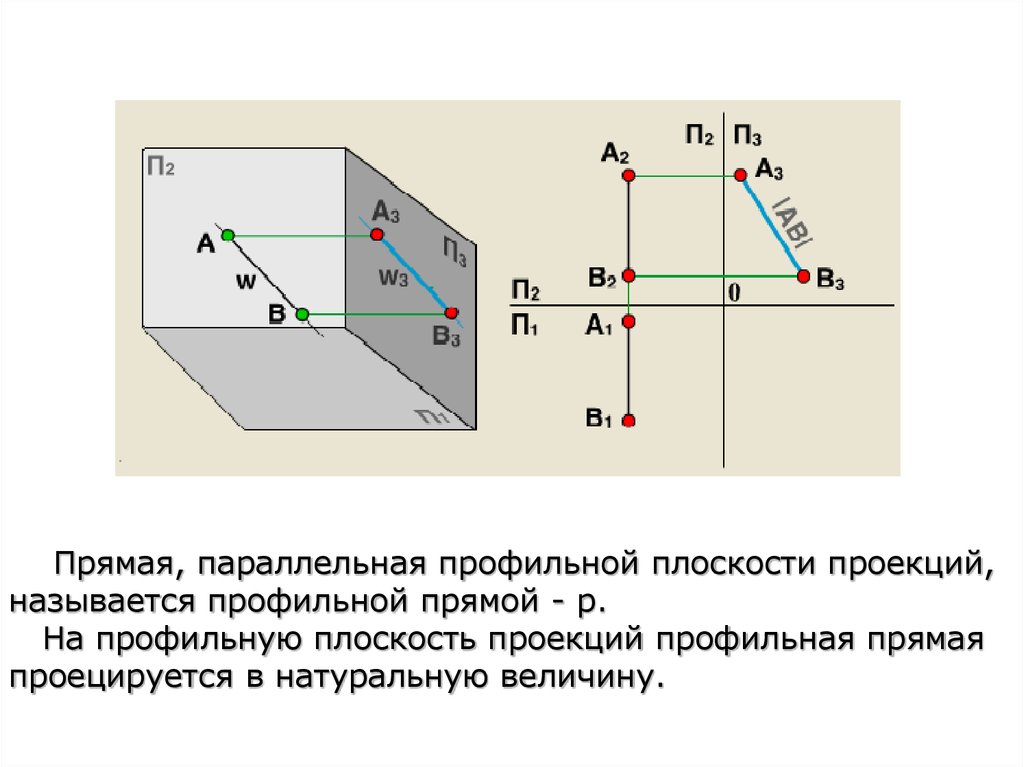
Прямая, параллельная профильной плоскости проекций,
называется профильной прямой - р.
На профильную плоскость проекций профильная прямая
проецируется в натуральную величину.

14.

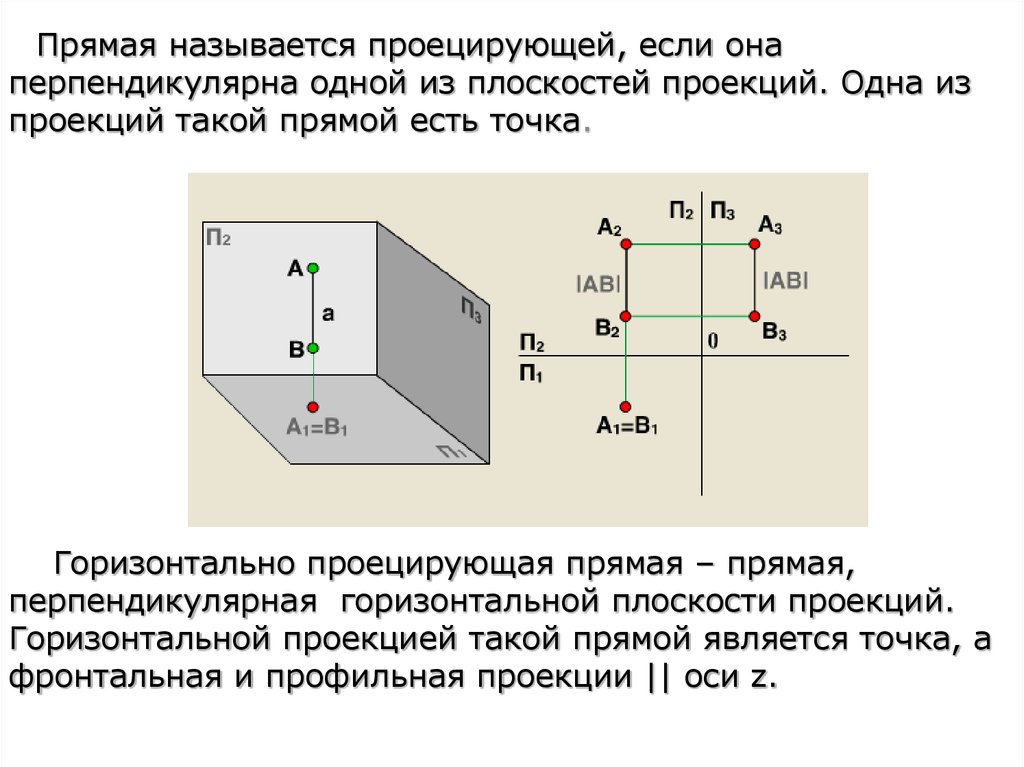
Прямая называется проецирующей, если она
перпендикулярна одной из плоскостей проекций. Одна из
проекций такой прямой есть точка.
Горизонтально проецирующая прямая – прямая,
перпендикулярная горизонтальной плоскости проекций.
Горизонтальной проекцией такой прямой является точка, а
фронтальная и профильная проекции || оси z.

15.

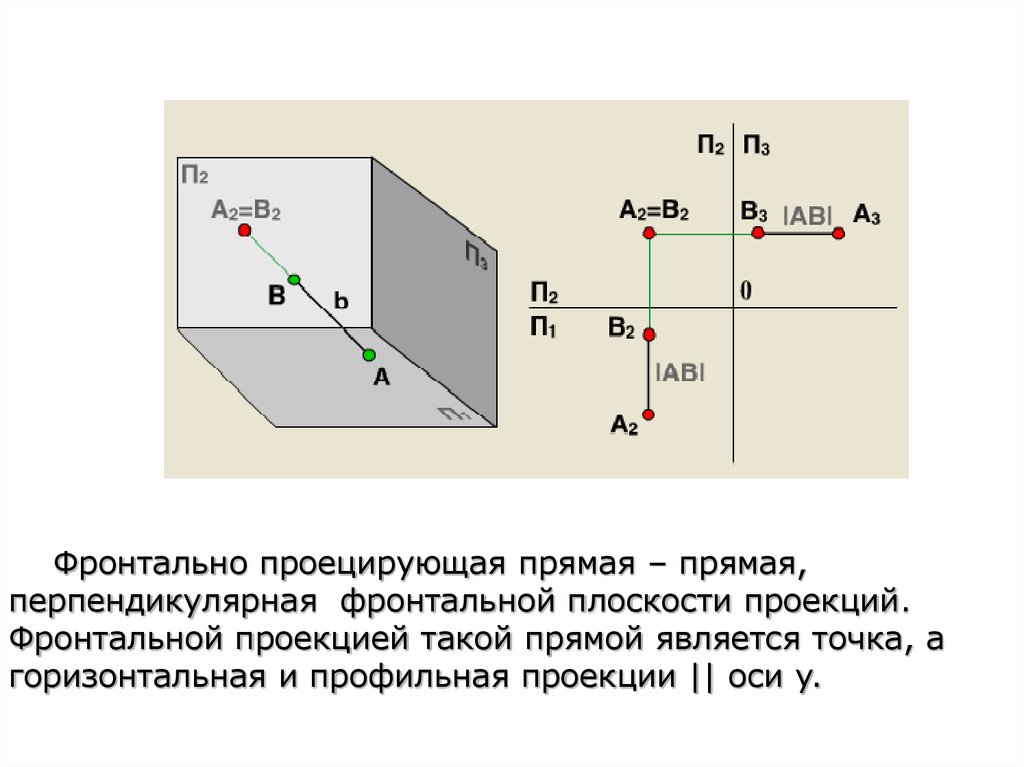
Фронтально проецирующая прямая – прямая,
перпендикулярная фронтальной плоскости проекций.
Фронтальной проекцией такой прямой является точка, а
горизонтальная и профильная проекции || оси y.

16.

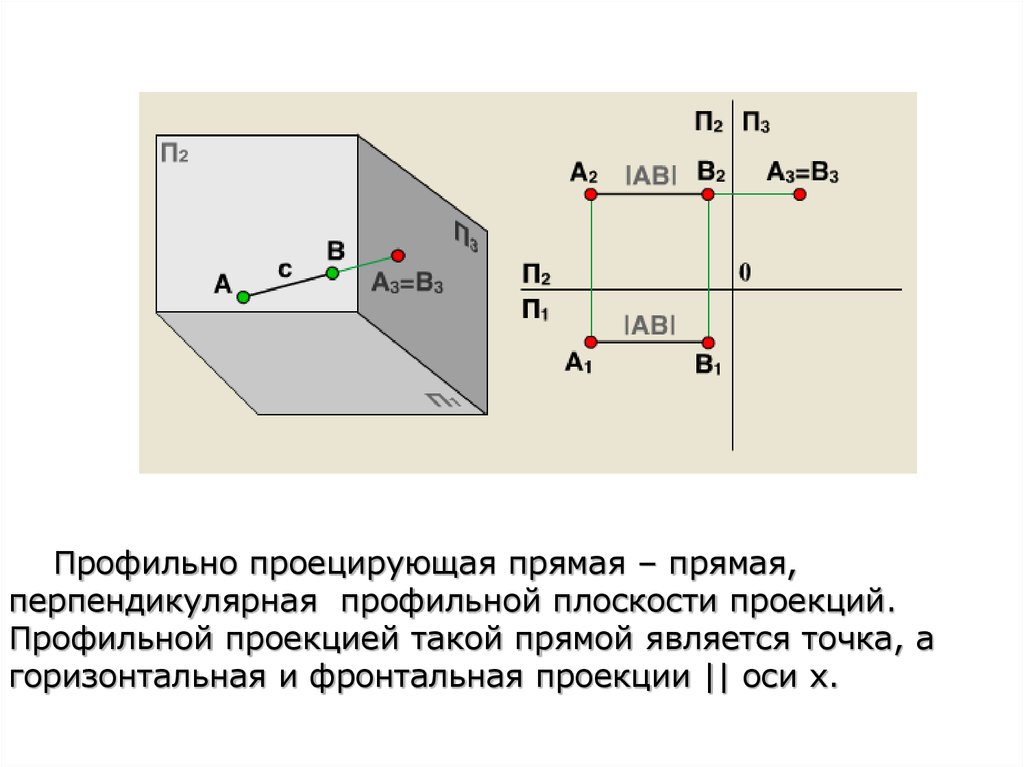
Профильно проецирующая прямая – прямая,
перпендикулярная профильной плоскости проекций.
Профильной проекцией такой прямой является точка, а
горизонтальная и фронтальная проекции || оси x.

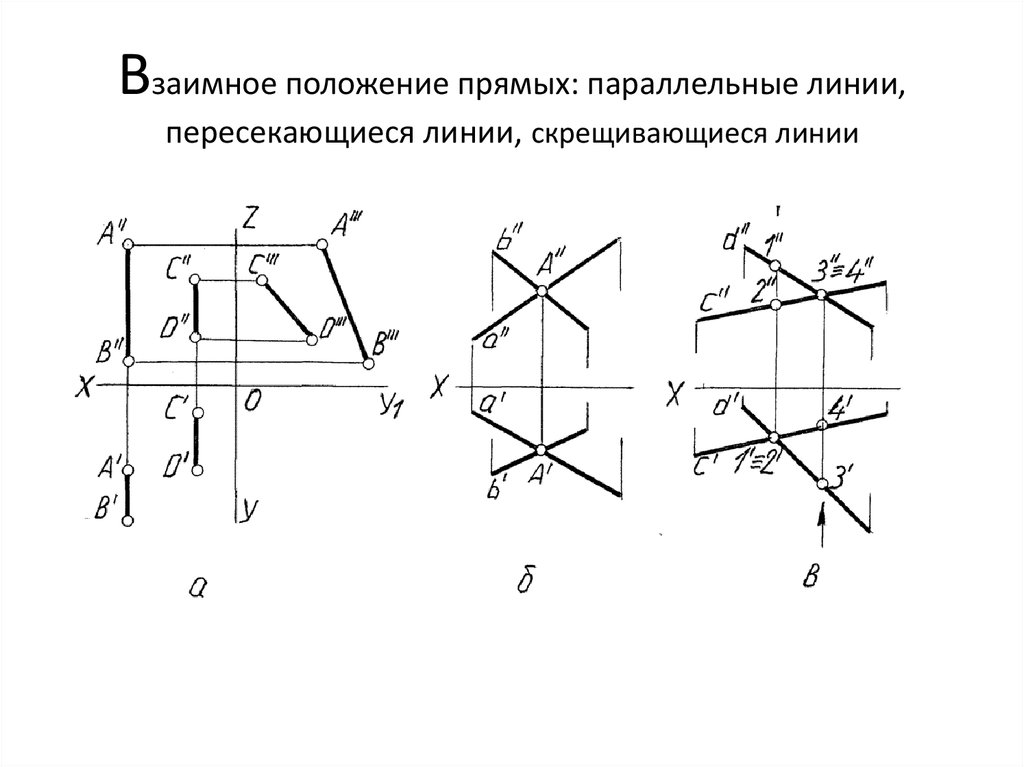
17. Взаимное положение прямых: параллельные линии, пересекающиеся линии, скрещивающиеся линии

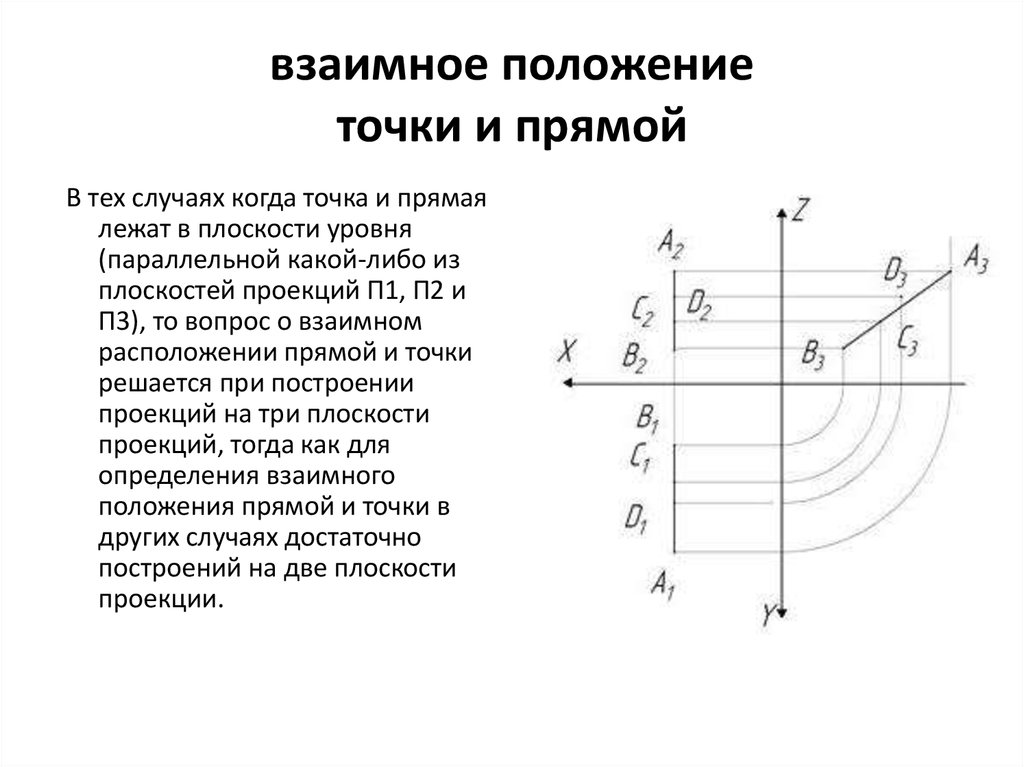
18. взаимное положение точки и прямой

В тех случаях когда точка и прямая
лежат в плоскости уровня
(параллельной какой-либо из
плоскостей проекций П1, П2 и
П3), то вопрос о взаимном
расположении прямой и точки
решается при построении
проекций на три плоскости
проекций, тогда как для
определения взаимного
положения прямой и точки в
других случаях достаточно
построений на две плоскости
проекции.

19.

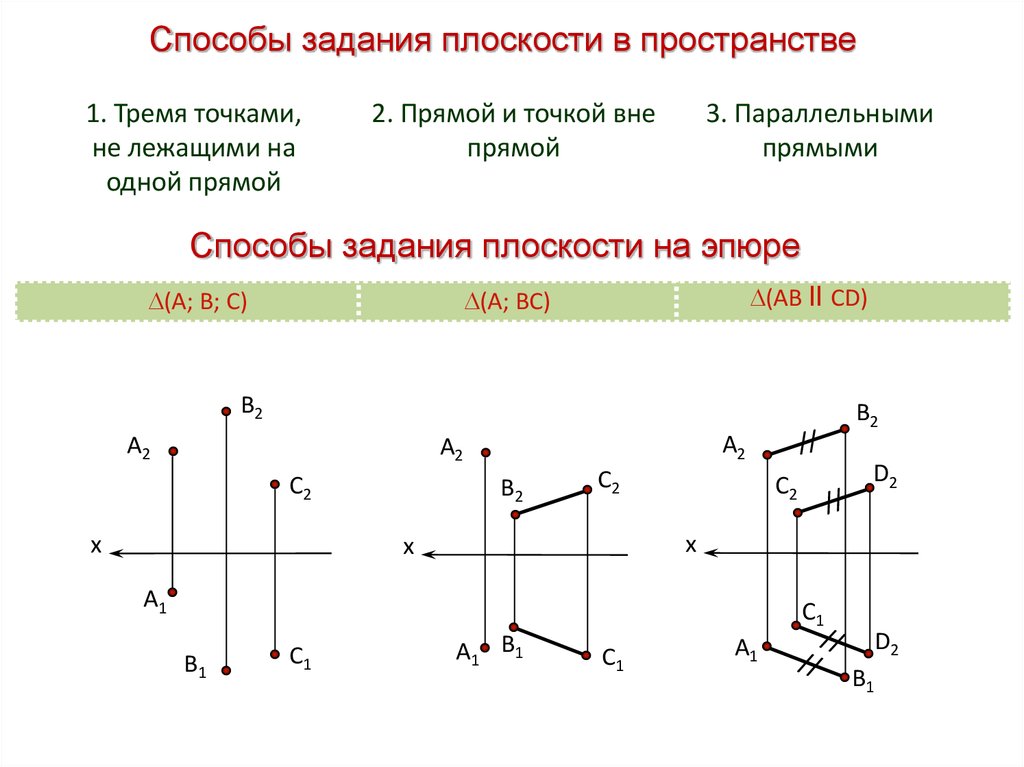
Способы задания плоскости в пространстве
1. Тремя точками,
не лежащими на
одной прямой
2. Прямой и точкой вне
прямой
3. Параллельными
прямыми
Способы задания плоскости на эпюре
(АВ ll СD)
(А; ВС)
(А; В; С)
В2
В2
А2
А2
А2
С2
х
В2
С2
D2
С2
х
х
А1
С1
В1
С1
А1 В 1
С1
D2
А1
В1

20.

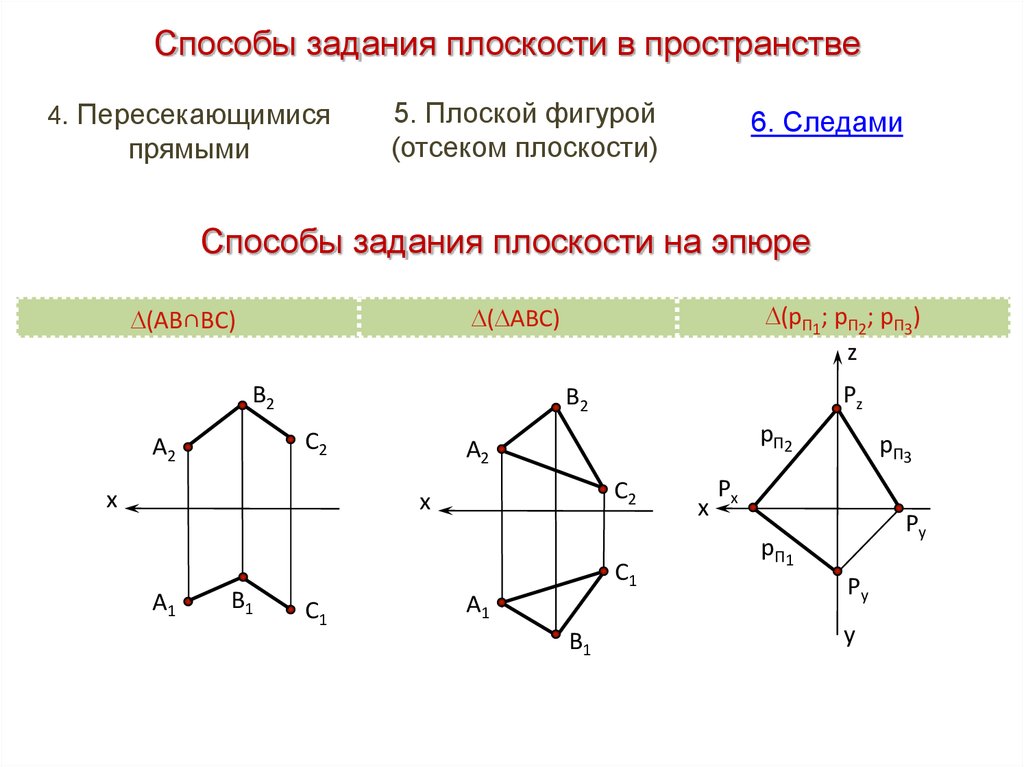
Способы задания плоскости в пространстве
4. Пересекающимися
прямыми
5. Плоской фигурой
(отсеком плоскости)
6. Следами
Способы задания плоскости на эпюре
В2
х
pП2
А2
С2
х
А1
В1
Pz
В2
С2
А2
(рП1; рП2; рП3)
z
( АВС)
(
АВС)
(АВ∩ВС)
(АВ BС)
С1
С1
А1
В1
х
pП3
Px
Py
pП1
Py
y

21.

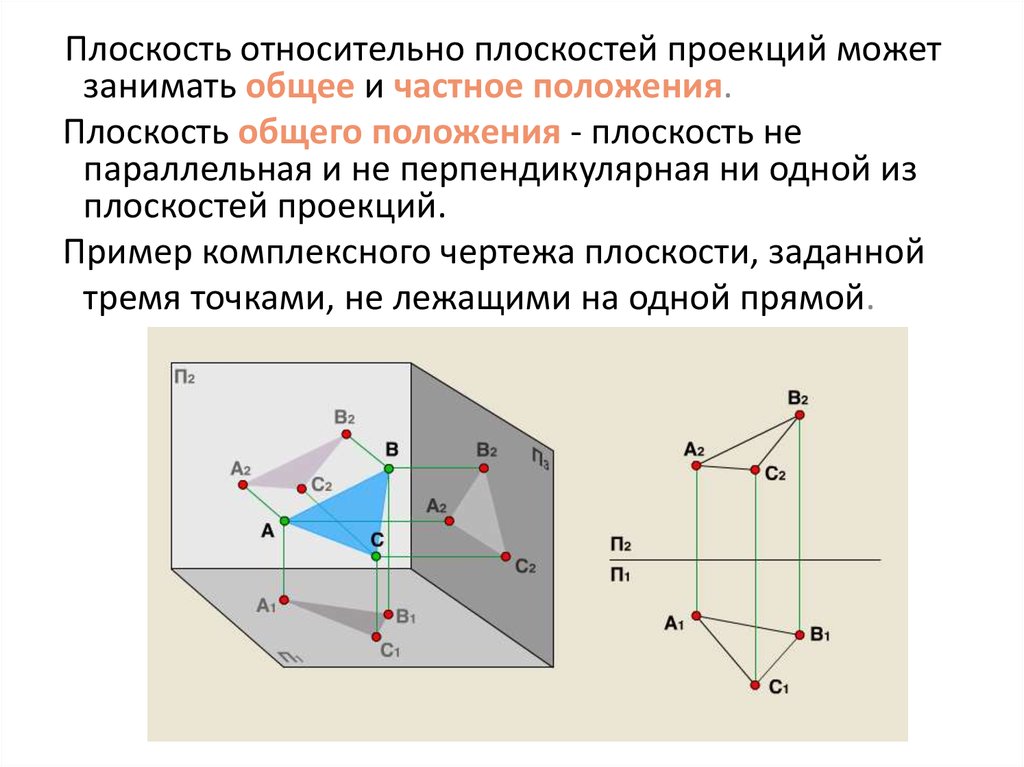
Плоскость относительно плоскостей проекций может
занимать общее и частное положения.
Плоскость общего положения - плоскость не
параллельная и не перпендикулярная ни одной из
плоскостей проекций.
Пример комплексного чертежа плоскости, заданной
тремя точками, не лежащими на одной прямой.

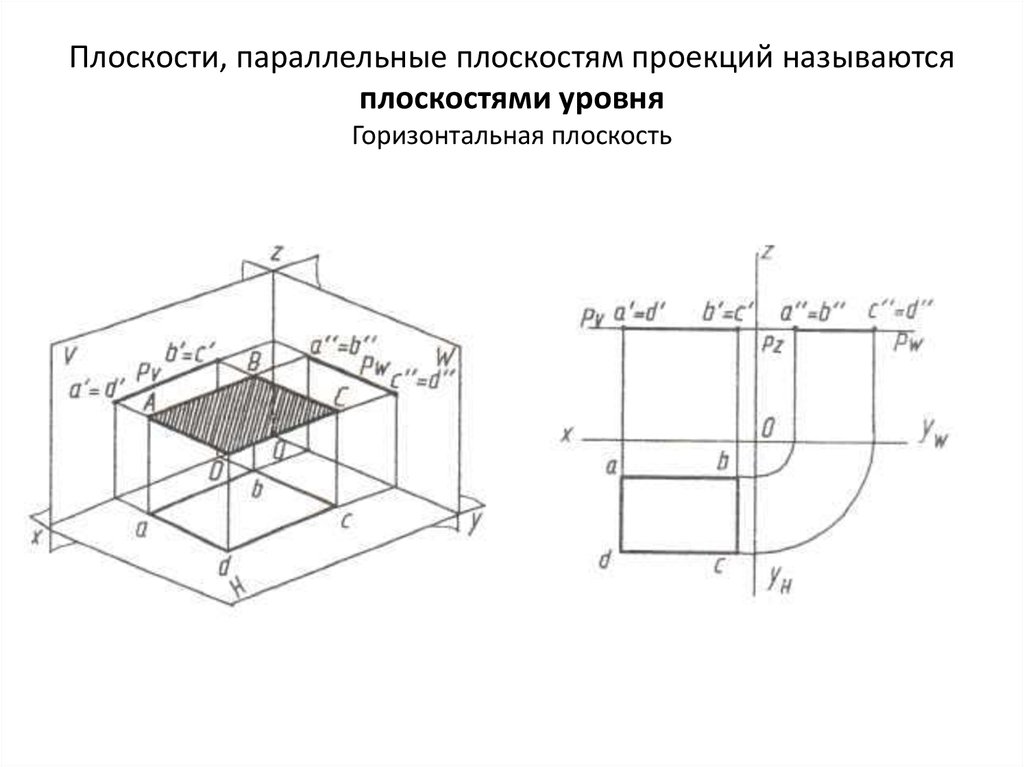
22. Плоскости, параллельные плоскостям проекций называются плоскостями уровня Горизонтальная плоскость

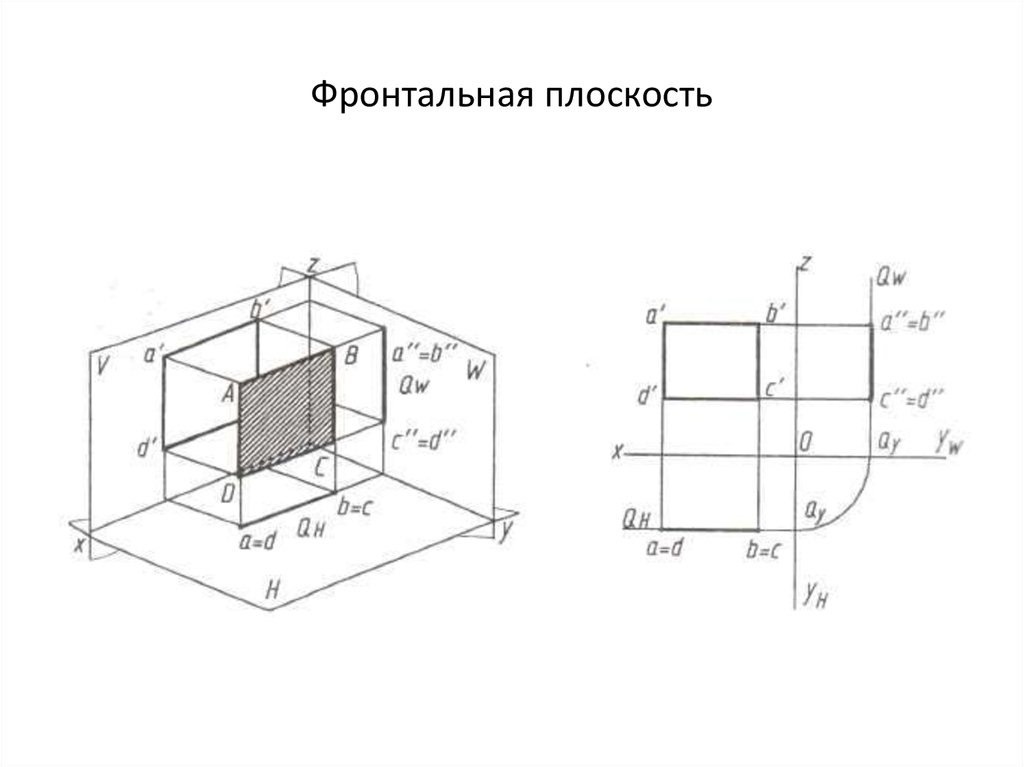
23. Фронтальная плоскость

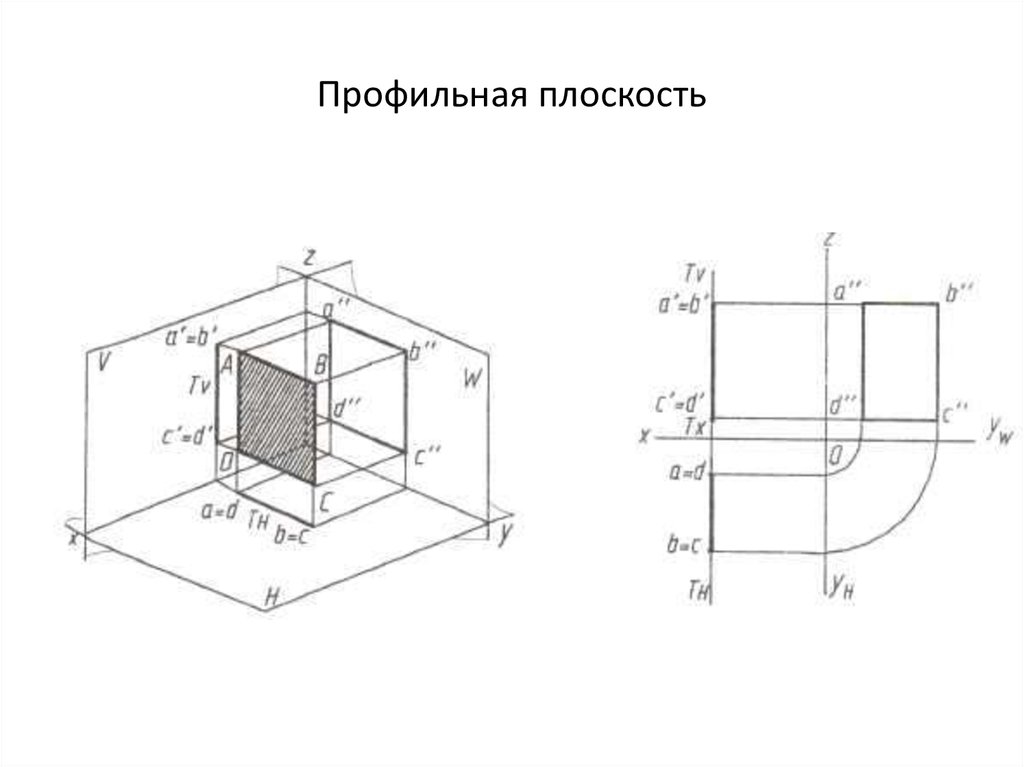
24. Профильная плоскость

25.

Фронтально проецирующая плоскость
перпендикулярна П2. На П2 проекция плоскости
прямая.

26.

Профильно- проецирующая плоскость перпендикулярна
П3. На П3 проекция плоскости прямая.

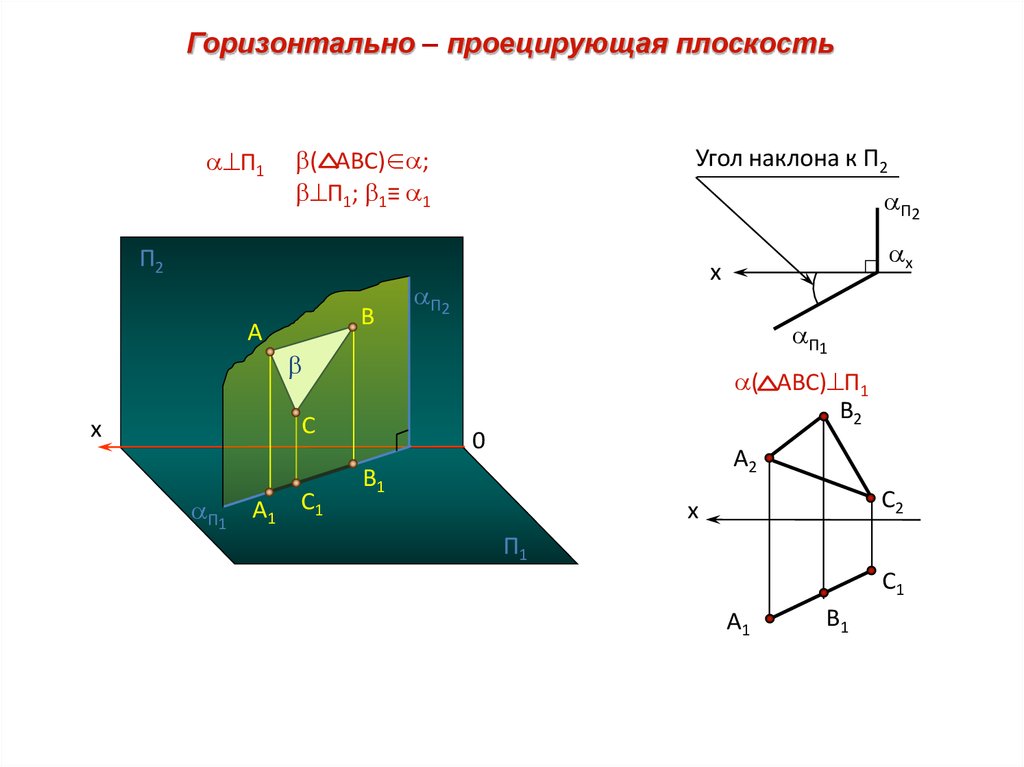
27.

Горизонтально – проецирующая плоскость
П1
( АВС)∈ ;
П1; 1≡ 1
Угол наклона к П2
П2
П2
B
A
П2
П1
x
C
П1 A1 С1
x
x
( АВС) П1
В2
0
А2
B1
С2
х
П1
С1
А1
В1

28. Взаимное расположение прямых и плоскостей.

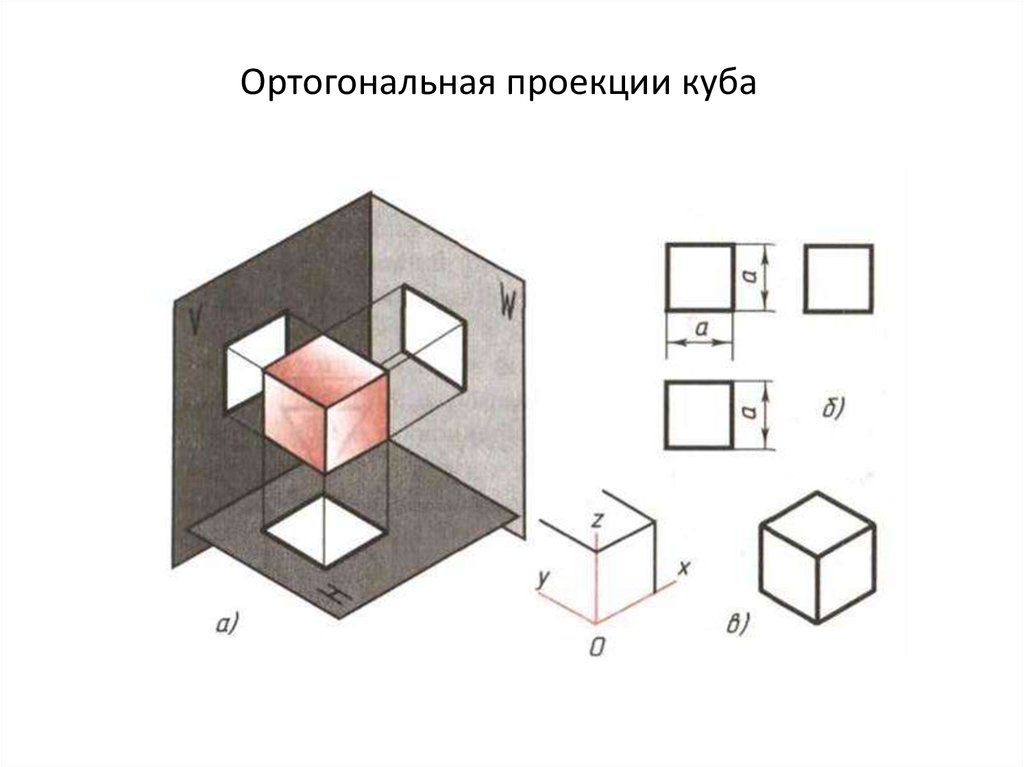
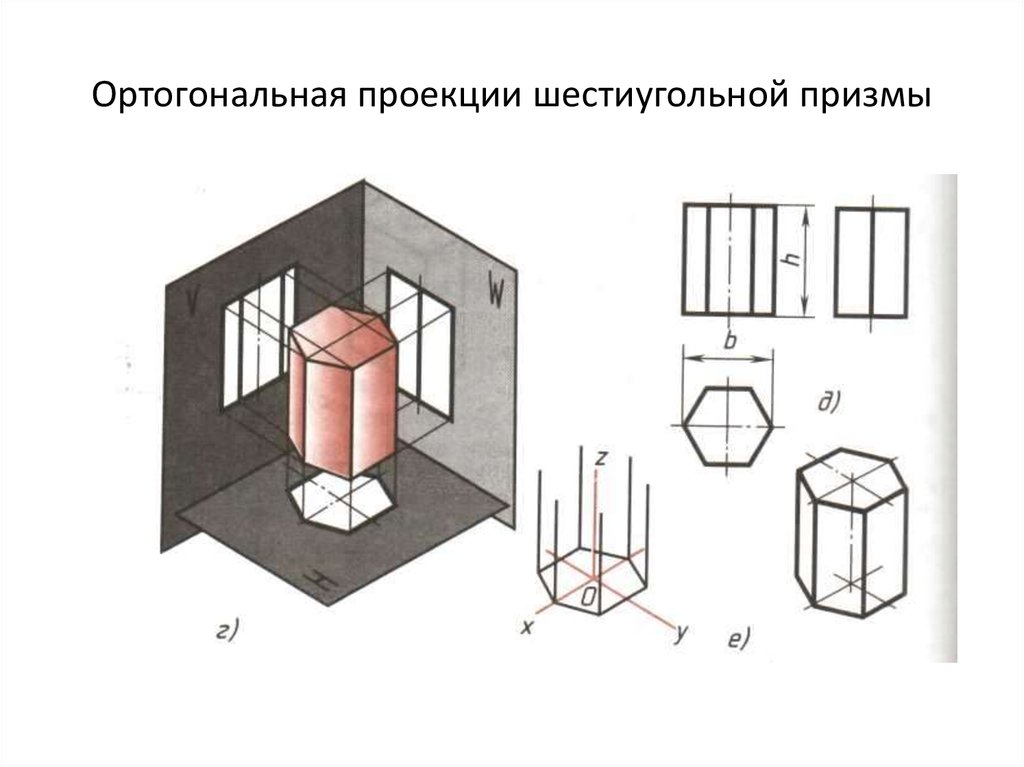
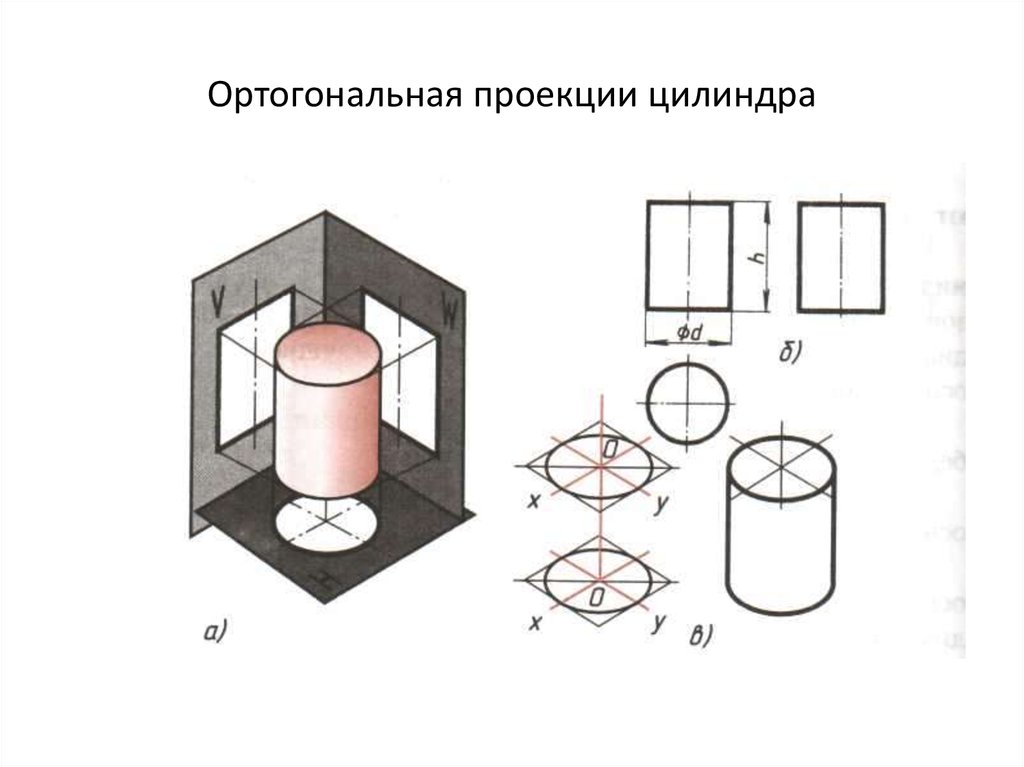
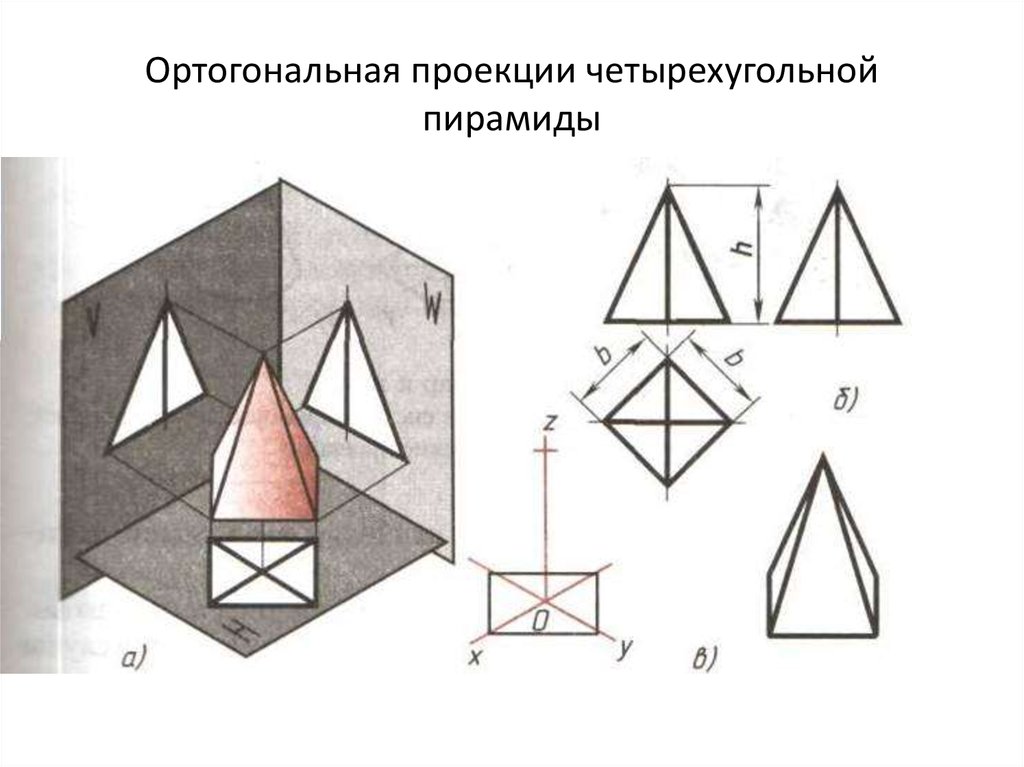
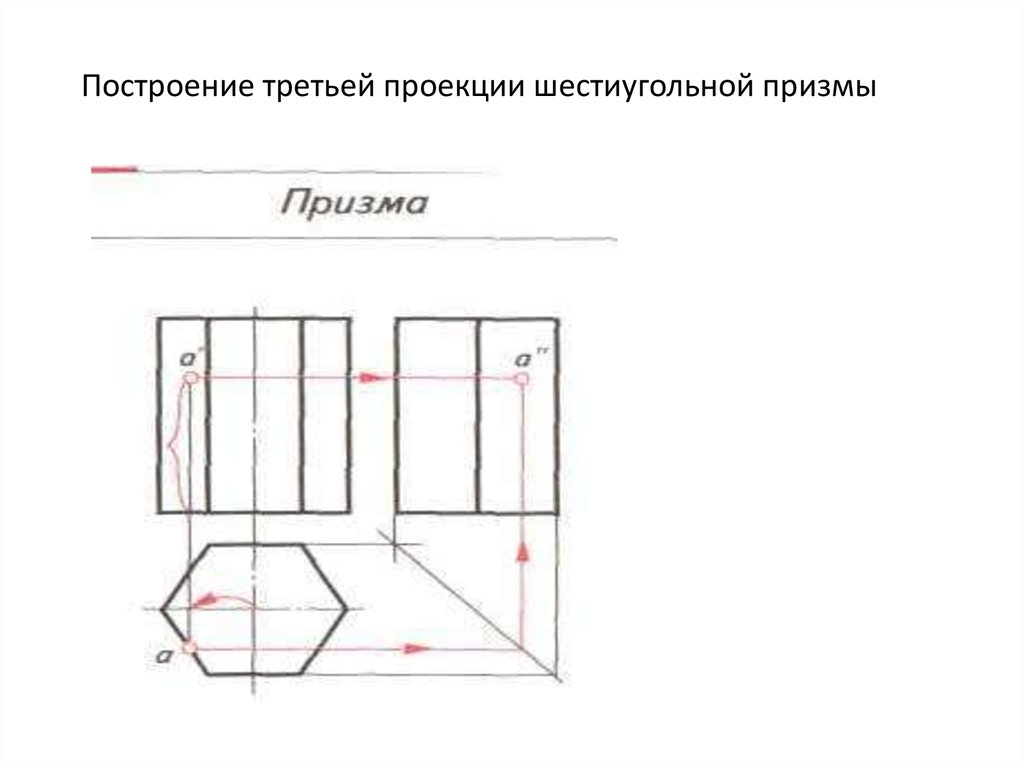
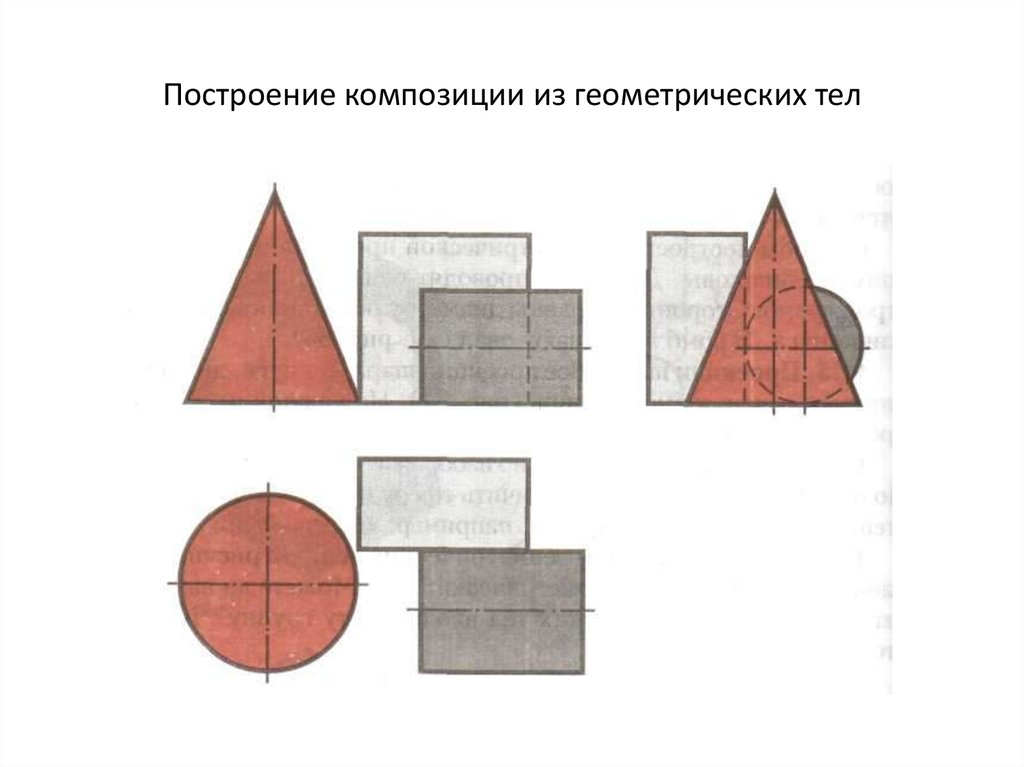
29. Проекции объемных тел

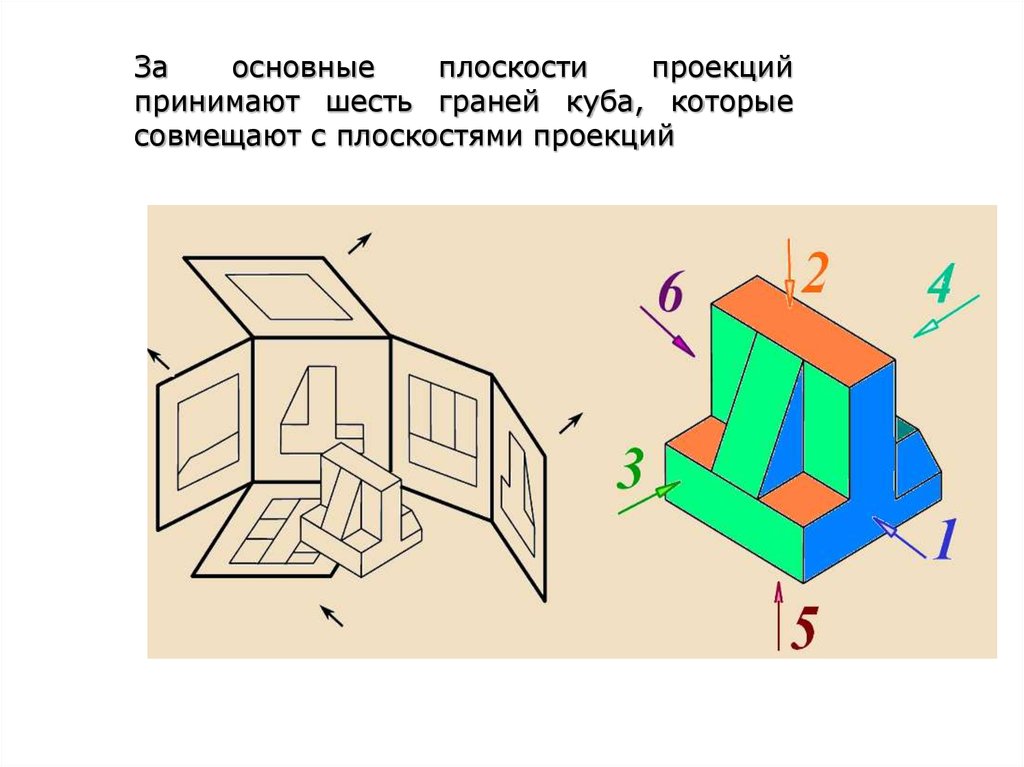
30.

За
основные
плоскости
проекций
принимают шесть граней куба, которые
совмещают с плоскостями проекций

31. Ортогональная проекции куба

32. Ортогональная проекции шестиугольной призмы

33. Ортогональная проекции цилиндра

34. Ортогональная проекции четырехугольной пирамиды

35. Построение третьей проекции шестиугольной призмы

36. Построение композиции из геометрических тел