Похожие презентации:
Площадь ортогональной проекции. Проекция
1. Проекция (лат. projectio — выбрасывание вперёд) — изображение трёхмерной фигуры на плоскости.
Проекция (лат. projectio — выбрасывание вперёд) —изображение трёхмерной фигуры на плоскости.
Проекционный метод изображения предметов основан на их
зрительном представлении.
Если соединить все точки предмета прямыми линиями (проекционн
ыми лучами) с постоянной точкой О (центр проекции), в которой предполагает
ся глаз наблюдателя, то на пересечении этих лучей с плоскостью получается проекция всех точек предмета.
Соединив эти точки прямыми линиями в том же порядке, как он
и соединены в предмете, получим на плоскости перспективное изображе
ние предмета или центральную проекцию.
Если центр проекции бесконечно удалён от картинной плоскости
говорят о параллельной проекции, а если при этом проекционные лучи па
дают перпендикулярно к плоскости — то об ортогональной проекции.
2. Теорема
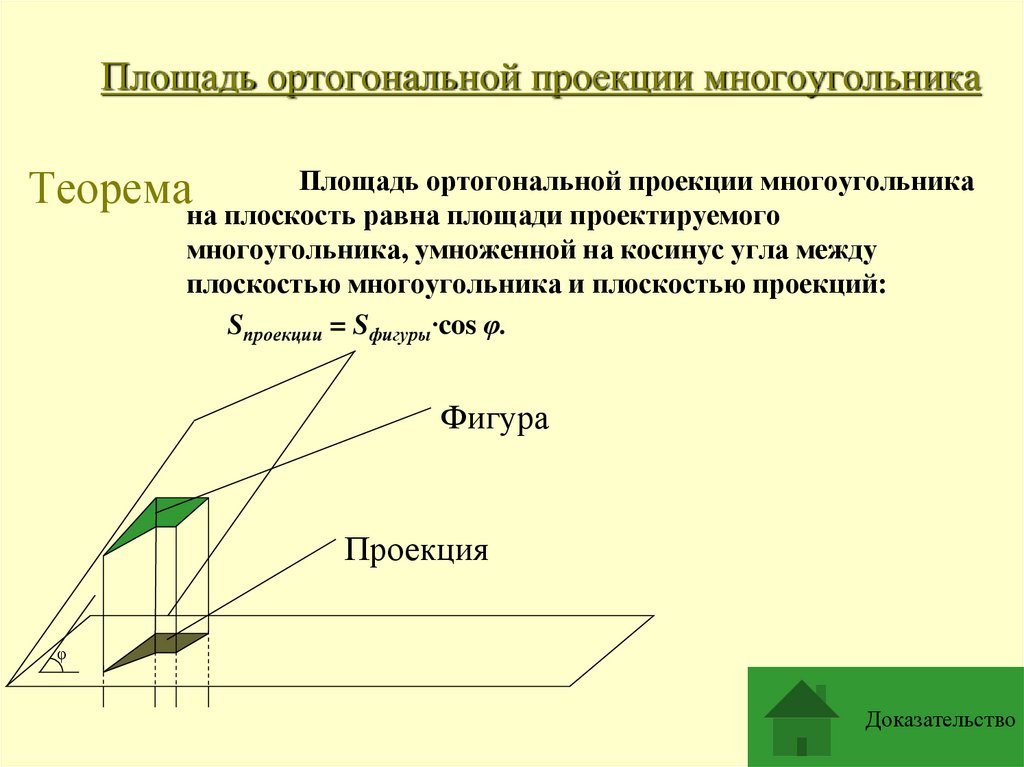
Площадь ортогональной проекции многоугольникаПлощадь ортогональной проекции многоугольника
Теоремана плоскость
равна площади проектируемого
многоугольника, умноженной на косинус угла между
плоскостью многоугольника и плоскостью проекций:
Sпроекции = Sфигуры·cos φ.
Фигура
Проекция
φ
Доказательство
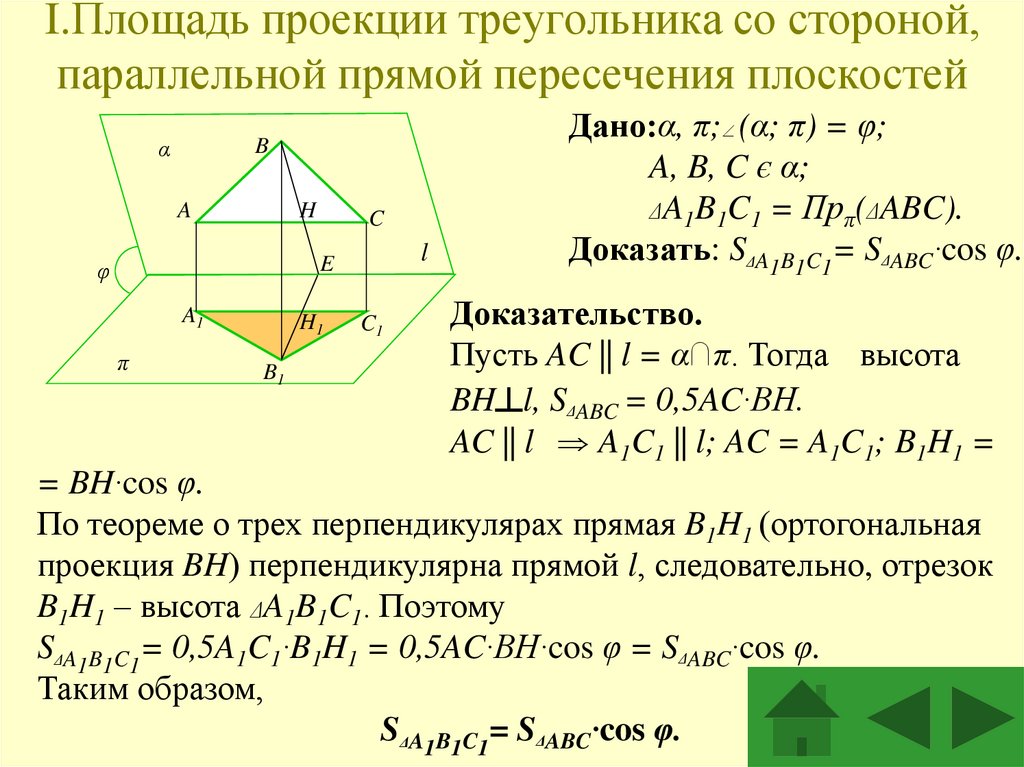
3. I.Площадь проекции треугольника со стороной, параллельной прямой пересечения плоскостей
αB
A
H
C
l
E
φ
A1
π
H1
B1
C1
Дано:α, π; (α; π) = φ;
A, B, C є α;
ΔA1B1C1 = Прπ(ΔABC).
Доказать: SΔA1B1C1= SΔABC·cos φ.
Доказательство.
Пусть AC || l = α∩π. Тогда высота
BH┴l, SΔABC = 0,5AC·BH.
AC || l A1C1 || l; AC = A1C1; B1H1 =
= BH·cos φ.
По теореме о трех перпендикулярах прямая B1H1 (ортогональная
проекция BH) перпендикулярна прямой l, следовательно, отрезок
B1H1 – высота ΔA1B1C1. Поэтому
SΔA1B1C1= 0,5A1C1·B1H1 = 0,5AC·BH·cos φ = SΔABC·cos φ.
Таким образом,
SΔA1B1C1= SΔABC·cos φ.
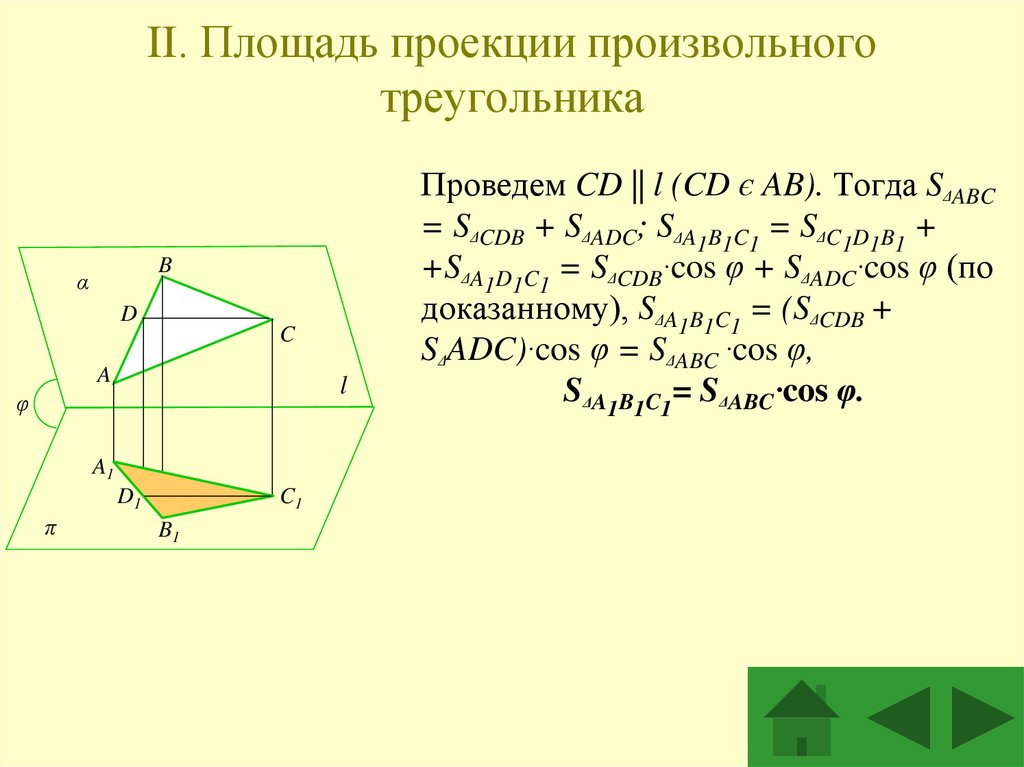
4. II. Площадь проекции произвольного треугольника
Bα
D
C
A
l
φ
A1
D1
π
C1
B1
Проведем CD || l (CD є AB). Тогда SΔABC
= SΔCDB + SΔADC; SΔA1B1C1 = SΔC1D1B1 +
+SΔA1D1C1 = SΔCDB·cos φ + SΔADC·cos φ (по
доказанному), SΔA1B1C1 = (SΔCDB +
SΔADC)·cos φ = SΔABC ·cos φ,
SΔA1B1C1= SΔABC·cos φ.
5.
Задача 4.089. Величина двугранного угла A(BC)M равна 60º. Отрезок AMперпендикулярен плоскости BCM. Найдите отношение площади треугольника ABC к
площади треугольника MBC.
Дано: A(BC)M = 60º; AM ┴(BCM).
Найти: SABC:SMBC.
Решение. AM ┴(BCM), значит, M –
ортогональная проекция A на плоскость
(MBC), следовательно, ΔMBC –
ортогональная проекция ΔABC на плоскость
(MBC). По теореме о площади
ортогональной проекции SMBC=SABC·cos 60º;
S ABC
SABC:SMBC =
= 2.
A
S ABC cos 60
C
B
M
Ответ: 2.
6. Задача 4.090. Квадрат ABCD перегнули по его диагонали BC так, что образовался острый двугранный угол α. Найдите отношение
площади ортогональнойпроекции треугольника ABC на плоскость BDC к площади треугольника BDC.
Дано: ΔBAC; ΔBDC; AB = BC = CD = AD; BAC =
BDC = 90º ; A(BC)D = α.
Найти: Sпр.ABC:SBDC.
Решение.
По теореме о площади ортогональной проекции
Sпр.ABC = SABC ·cos α.
ABC = ΔBDC (по 3 сторонам).
Sпр.ABC:SBDC = (SABC ·cos α)/ SABC = cos α.
A
Δ
C
B
Ответ: cos α.
D
7. Задача 4.094. Сумма площадей всех боковых граней правильной пятиугольной пирамиды в шесть раз больше площади ее основания.
Найдите двугранный угол при ребреоснования пирамиды.
Дано: PQRSTU – правильная пирамида;
SPQR + SPRS + SPST + SPTU + SPUQ = 6SQRSTU.
Найти: φ = P(UT)R.
Решение.
P
Пусть PO┴(QUT).
По определению боковые грани равны, SPQR =
=SPRS = …; SOQR = SORS = ….
SQRSTU = 5SOQR = 5SPQR ·cos φ (т. к. ΔOQR –
ортогональная проекция ΔPQR);
R
Q
S
O
U
T
5SPQR = 6·5SPQR ·cos φ;
cos φ = 1/6;
φ = arccos 1/6.
Ответ: arccos 1/6.
8. Задача 4.095. В правильной треугольной пирамиде MABC все боковые ребра образуют с плоскостью основания углы, равные 60º.
Найдите отношение площадиоснования пирамиды к площади сечения, проведенного через вершины B и C
перпендикулярно ребру MA.
Дано: MABC – правильная треугольная пирамида; MAO = MBO = MCO =
60º; сечение BCH┴AM (H Є AM).
Найти: SABC : SBCH.
Решение. Пусть AB = BC = AC = a; AM = BM = CM = b. (BCH)┴AM,
следовательно NH┴AM; из ΔANH ANH = 180º - 60º - 90º = 30º. Вследствие
симметрии BH
= CH; BN = NC (т. к. AN – медиана), т. е. HN – высота,
M
HN┴BC; AN┴BC, значит, угол между (BCH) и
b
b
b
H
60º
a
A
C
O
a
a
B
N
(ABC) равен ANH= 30º. AH┴(BCH),
следовательно, ΔBCH – это ортогональная
проекция ΔABC на плоскость (BCH); SBCH =
3
=SABC·cos ANH =
SABC.
2
2 3
SABC : SBCH =
.
3
Ответ:
2 3
.
3
9. Задача 4.096.а) В правильной треугольной пирамиде MABC проведено сечение через середину ребра MC и вершины A и B. Площадь этого
сечения составляет 8/9площади основания пирамиды. Определите: угол наклона плоскости сечения к плоскости
основания пирамиды.
Дано: МАВС – правильная пирамида; О – центр основания
АВС; К - середина МС; Р – середина АВ; (АВК) – сечение.
В правильной треугольной пирамиде MABC проведено
сечение через середину ребра MC и вершины A и B. SΔАВК =
8
/9 SΔАВС.
М
Найти: ( ABC; ABR)
Решение.
MO – высота пирамиды, тогда СРК = φ = ( ABC; ABR) . При
К
этом. SΔАВК = 8/9 SΔАВС. КР = 8/9РС.
Если АВ = а, то
Н
А
φ
Р
α
a 3
2
и
KP
8a 3 4a 3
9 2
9 .
С середина МС и КН||ОМ, то НС = ОН = ОР=
О
В
CP
a 3
РН = 3
3
arccos
4.
. Тогда
a 3
3
cos 3
4a 3 4
9
,
откуда
Так как К -
a 3
= 6
, значит,
arccos
3
4 .Ответ:
10. Задача 4.096.в) В правильной треугольной пирамиде MABC проведено сечение через середину ребра MC и вершины A и B. Площадь этого
сечения составляет 8/9площади основания пирамиды. Определите: угол наклона бокового ребра пирамиды к
плоскости её снования .
Дано: МАВС – правильная пирамида; О – центр основания
АВС; К - середина МС; Р – середина АВ; (АВК) – сечение.
В правильной треугольной пирамиде MABC проведено
сечение через середину ребра MC и вершины A и B. SΔАВК = 8/9
SΔАВС.
Найти: ( ABC; MC)
М
Решение.
MCP ( ABC; MC) , так как МО – перпендикуляр, прямая СР
– проекция прямой МС на плоскость (АВС). Sсеч = 8/9 SАВС,
Sсеч = ( аРК)/2, а площадь SАВС находим по формуле
К
площади равностороннего треугольника. Откуда находим,
KP
Н
А
φ
Р
О
α
С
Из
В
8a 3 4 a 3
9 2
9
CKH
2 7
arctg 3
4a 3 7
KH PK sin
9
4 2 7
CH
CH
3
a 3
6
tg
.
Ответ: α =
2 7
arctg 3
.
, откуда α =
11.
Задача 4.097. В правильной четырехугольной пирамиде МАВСD через ребро АВи середину ребра МС проведено сечение, площадь которого в 1,125 раза больше площади
основания. Найдите величину угла между плоскостью сечения и плоскостью основания, а
также угол при ребре основания данной пирамиды.
М
Дано: MABCD – правильная пирамида, К – середина МС,
(АВК) – сечение, Sсеч = 1,125SABCD; МО – высота.
Найти: K ( AB)C , M ( AC ) A .
Решение.
Пусть АВ = а, Н – середина АВ, F – середина CD. АВ||ЕК по
K
теореме о пересечении двух плоскостей третьей, АЕ = ВК
P
вследствие симметрии сечение АВЕК – равнобедренная
E
B
трапеция с основаниями АВ = а и КЕ = 0,5АВ = 0,5а (так как
C
КЕ||АВ и К – середина СМ, то есть КЕ – средняя линия MDC )
α
O
φ
F
a
H
T
a
AB KE
3a
PH 2 PH PH (Р – середин
Тогда Sсеч = SABKE =
2
2
4
A
D
КЕ).
9
3a
9
3a
Имеем: S ABKE S ABCD PH a 2 PH .
8
4
8
2
3
a
Так как Р – середина MF и PT||OM, то НТ = а, FT = ,
4
4
12. Задача 4.097.В правильной четырехугольной пирамиде МАВСD через ребро АВ и середину ребра МС проведено сечение, площадь которого
в 1,125 раза больше площадиоснования. Найдите величину угла между плоскостью сечения и плоскостью основания, а
также угол при ребре основания данной пирамиды.
Дано: MABCD – правильная пирамида, К – середина МС,
(АВК) – сечение, Sсеч = 1,125SABCD; МО – высота.
Найти: K ( AB)C , M ( AC ) A .
М
K
P
E
B
C
D
F
α
O
φ
T
A
H
При этом PHT – линейный угол двугранного угла,
образованного секущей плоскостью и плоскостью
основания пирамиды, PFT – линейный угол
двугранного угла при ребре основания пирамиды.
Решение (продолжение). Из прямоугольного ΔРНТ
3
a
HT 4
1
60 .
находим: cos
HP 3 a 2
2
PT PH sin 60
Из прямоугольного ΔРFТ находим: tg α
=
FP
FP
3
3
a
= 2 2 3 3 arctg(3 3 ).
a
4
Ответ: 60 ; arctg(3 3 ).
13.
Задача 4.098. К плоскости треугольника АВС по одну от нее проведеныперпендикуляры АК и ВМ. Найдите угол между плоскостями АВС и СКМ, если АВ
= АС = ВС = АК = 0,5ВМ
К
P
A
φ
C
Дано: ΔАВС, АК┴(АВС), ВМ┴(АВС). АВ = АС = ВС = АК =
=0,5ВМ.
Найти: ( ABC;CKM ) .
M
Решение. Пусть Р = МК∩АВ = МК∩АВС. Так как АК||BM и
ВМ = 2АК, то АР = АВ = АС. Это означает, что ΔАРС –
равнобедренный.Так как CAP 120 , то ACP 30 .
H Значит, BCP 90 . Тогда по теореме о трех
перпендикулярах МС┴СР, поэтому BCM - линейный
угол двугранного угла М(СР)В.
Пусть АВ = а. Тогда ВМ = 2а. МС = а 5 , значит,
BC 1
5
5
B cos
, откуда φ = arccos
.
MC 5 5
5
5
Ответ: arccos
5
14. Задача 4.100. Через вершину A квадрата ABCD проведен к его плоскости перпендикуляр AM, равный 10. Угол между плоскостями ABC и
MBC равен 45º. Найдитеплощадь треугольника MBC.
M
10
D
A
B
Дано: ABCD – квадрат; AM┴(ABC); AM = 10;
(ABC; MBC) = 45º.
Найти: SMBC.
Решение. (ABC; MBC) = MBА = 45º., АВ = 10
SABC = 0,5АВ·ВС = 0,5·10·10= 50
МА – перпендикуляр к плоскости (АВС), значит, ΔABC –
C ортогональная
проекция ΔMBC на плоскость
(ABC), SАBC
= SМBC·cos (ABC; MBC) ; SМBC = SАBC :cos (ABC; MBC)
= 50 2
Ответ: 50 2.
15. Задача 4.101. В основании прямого параллелепипеда квадрат со стороной a. Через середины двух смежных сторон основания проведена
плоскость, пересекающая три боковых ребра параллелепипеда и наклоненная кплоскости основания под углом φ. Найдите площадь сечения.
B1
A1
R
C1
D1
S
B
C
Q
A
T
Дано: ABCDA1B1C1D1 – прямой параллелепипед;
ABCD – квадрат; AB = a. Сечение PQRST (рис.);
(PQR; ABC) = φ; P –середина AD; T – середина
DC.
Найти: SPQRST.
Решение. PABCT – ортогональная проекция
сечения PQRST, следовательно,
S PABCT = Sсеч cos φ, S PABCT = 7/8 a2, Sсеч cos φ
7a2
=7/8 a2 , Sсеч =
8 cos
Ответ: 7 a 2 .
8 cos
P
D
U
16.
Задача 4.105. В правильной треугольной призме, каждое ребро которой равно 9дм, постройте сечение, проходящее через сторону основания и середину отрезка,
соединяющего центры оснований призмы. Найдите: а) угол между плоскостью сечения и
плоскостью основания призмы; б) площадь сечения.
Дано: АВСА1В1С1 - правильная треугольная призма, ребро 9
дм, О – центроид АВС, О1 – центроид А1В1С, Е – середина
ОО1
H
B1
Найти: E(BC) A ; Sα.
A1
L
O1 K1
φ
Решение.
M
C1
К – середина ВС и К1 – середина В1С1. Пересечением
плоскости ВСЕ с гранью А1В1С1 является отрезок МН,
который параллелен отрезку В1С1 и В1С1 = 3МН, откуда
1
следует, что S A MH S A B C
1
9 1 1 1
8
8 81 3
φ
C
S B MHC S A B C
18 3 .
O
A
1
1
1
1
1
9
9 4
K
B
17.
Задача 4.105. В правильной треугольной призме, каждое ребро которой равно 9дм, постройте сечение, проходящее через сторону основания и середину отрезка,
соединяющего центры оснований призмы. Найдите: а) угол между плоскостью сечения и
плоскостью основания призмы; б) площадь сечения.
A1
L
M
A
H
O1
φ
B1
K1
C1
φ
O
C
K
B
Так как А1К1┴В1С1, В1С1|| МН, то А1К1┴МН, значит, KL┴МН
(где L=MH∩А1К1). Тогда по теореме о трех
перпендикулярах KL┴ВС, поэтому AKL – линейный
угол двугранного угла между секущей плоскостью и
плоскостью основания призмы. Это означает, что
S B MHC
1 .
S BMHC 1
cos
Найдем φ.
1
9 3 3 3
Так как OK AK
, ОЕ = 4,5, то
3
3 2
2
OE 4,5
tg φ =
3 , значит, φ = 60?. Тогда
OK 3 3
2
18 3
Sñå÷ S BMHC
36 3
cos 60
Ответ: φ = 60; Sñå÷ 36 3
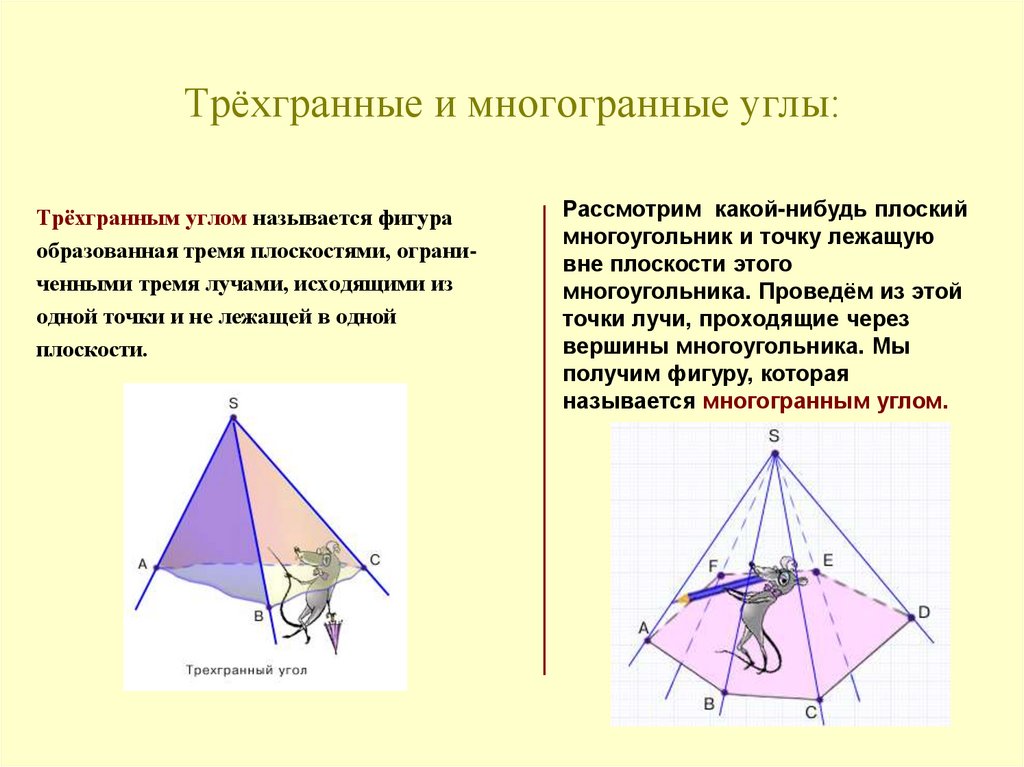
18. Трёхгранные и многогранные углы:
Трёхгранным углом называется фигураобразованная тремя плоскостями, ограниченными тремя лучами, исходящими из
одной точки и не лежащей в одной
плоскости.
Рассмотрим какой-нибудь плоский
многоугольник и точку лежащую
вне плоскости этого
многоугольника. Проведём из этой
точки лучи, проходящие через
вершины многоугольника. Мы
получим фигуру, которая
называется многогранным углом.
19.
Трёхгранный угол — это часть пространства, ограниченнаятремя плоскими углами с общей вершиной и попарно
общими сторонами, не лежащими в одной плоскости. Общая
вершина О этих углов называется вершиной трёхгранного
угла. Стороны углов называются рёбрами, плоские углы при
вершине трёхгранного угла называются его гранями. Каждая
из трёх пар граней трёхгранного угла образует двугранный
угол
20.
Определение.Трехгранные углы называются равными если равны
все их соответствующие плоские и двугранные
углы.
Признаки равенства трехгранных углов.
Трехгранные углы равны, если у них
соответственно равны:
1) два плоских угла и двугранный угол между ними;
2) два двугранных угла и плоский угол между ними;
3) три плоских угла;
4) три двугранных угла.
21.
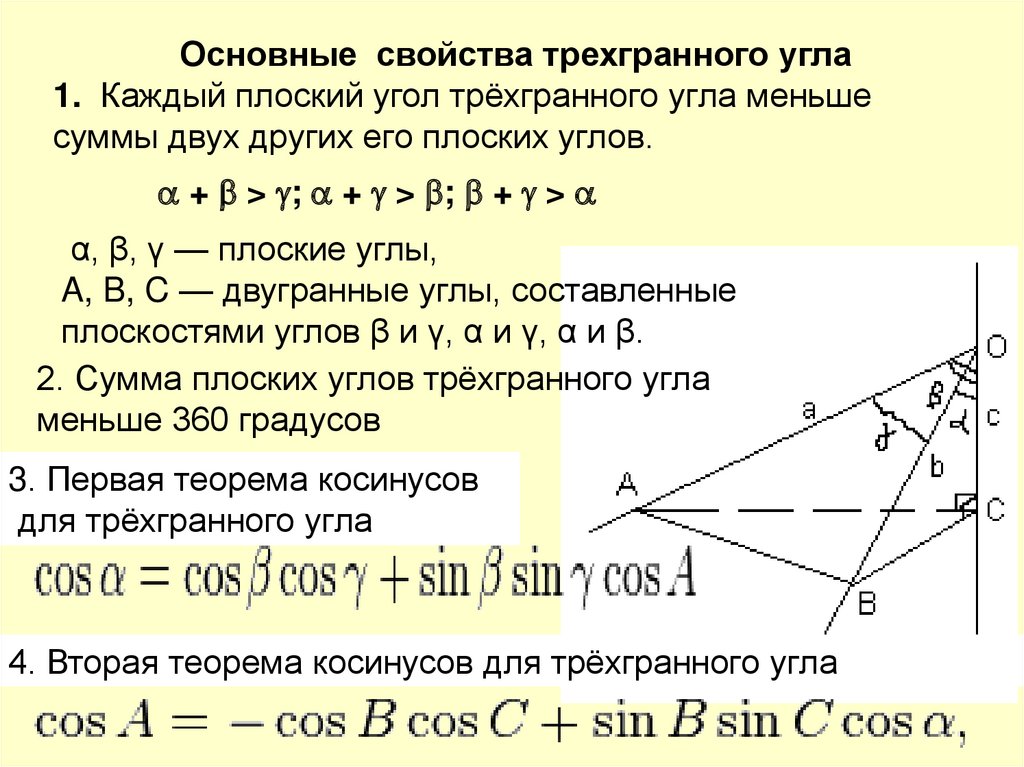
Основные свойства трехгранного угла1. Каждый плоский угол трёхгранного угла меньше
суммы двух других его плоских углов.
+ > ; + > ; + >
α, β, γ — плоские углы,
A, B, C — двугранные углы, составленные
плоскостями углов β и γ, α и γ, α и β.
2. Сумма плоских углов трёхгранного угла
меньше 360 градусов
3. Первая теорема косинусов
для трёхгранного угла
4. Вторая теорема косинусов для трёхгранного угла
22.
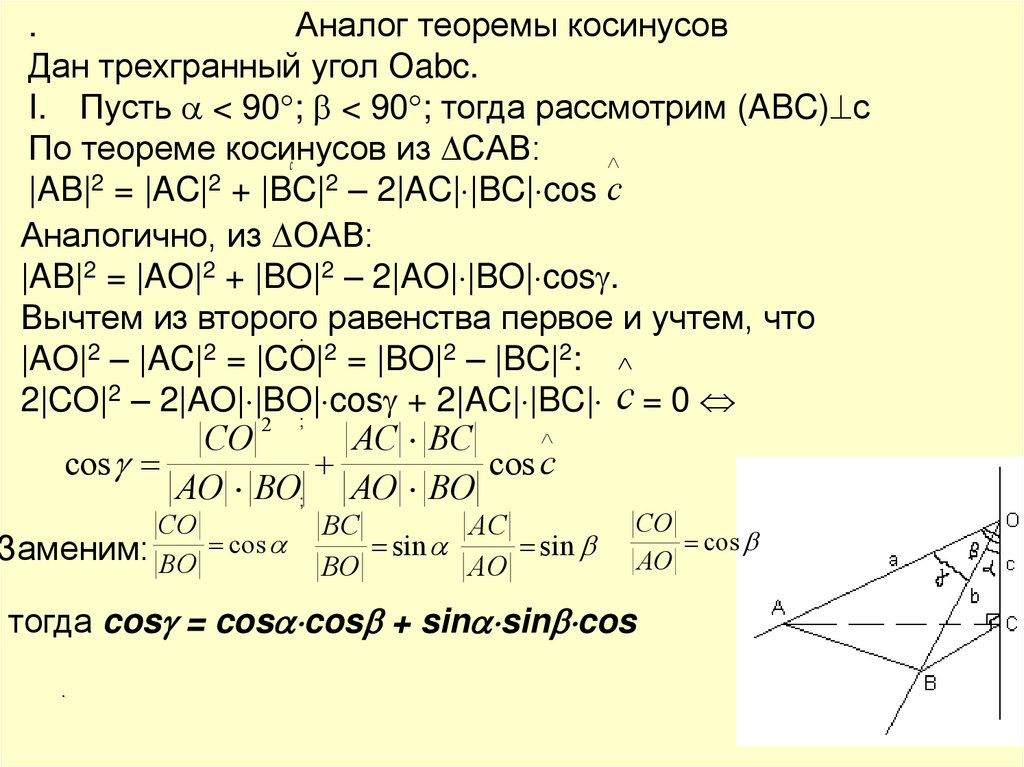
.Аналог теоремы косинусов
Дан трехгранный угол Оabc.
I. Пусть < 90 ; < 90 ; тогда рассмотрим (ABC) с
По теореме косинусов
из CАВ:
c
|AB|2 = |AC|2 + |BC|2 – 2|AC| |BC| cos c
Аналогично, из OАВ:
|AB|2 = |AO|2 + |BO|2 – 2|AO| |BO| cos .
Вычтем из второго равенства первое и учтем, что
;
2
2
|AO| – |AC| = |CO|2 = |BO|2 – |BC|2:
2|CO|2 – 2|AO| |BO| cos
+ 2|AC| |BC| c = 0
2 ;
CO
AC BC
cos
cos c
AO BO; AO BO
Заменим:
CO
cos
BO
BC
AC
sin
sin
BO
AO
CO
cos
AO
тогда cos = cos cos + sin sin cos
.
23.
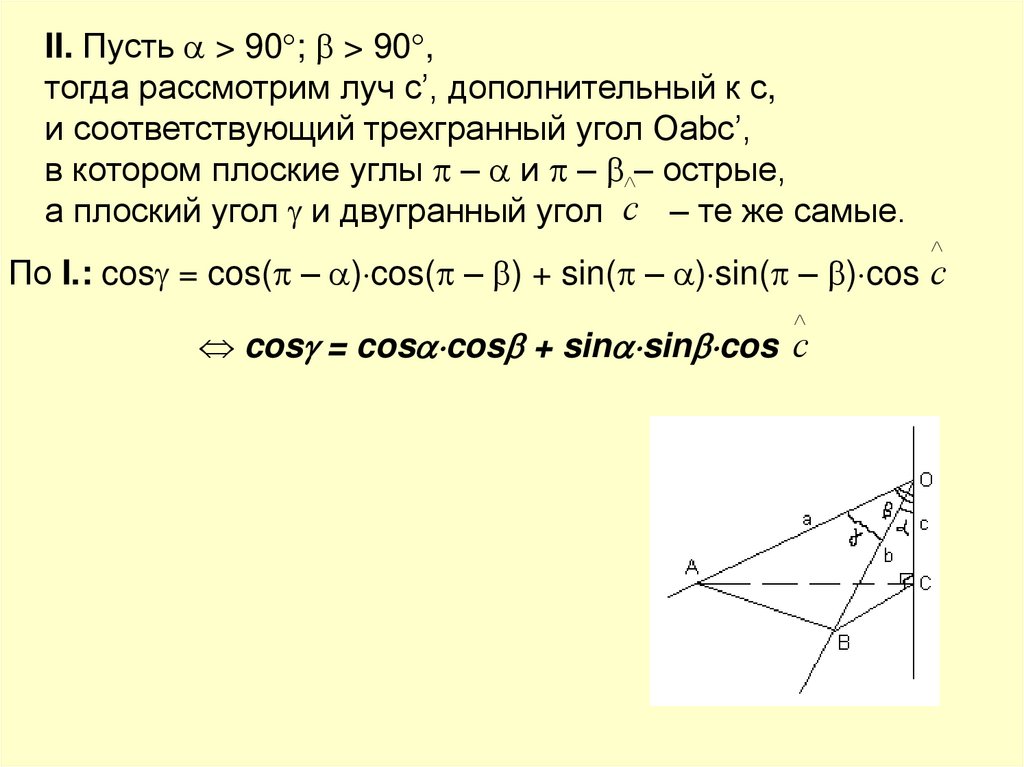
II. Пусть > 90 ; > 90 ,тогда рассмотрим луч с’, дополнительный к с,
и соответствующий трехгранный угол Оаbс’,
в котором плоские углы – и – – острые,
а плоский угол и двугранный угол c – те же самые.
По I.: cos = cos( – ) cos( – ) + sin( – ) sin( – ) cos c
cos = cos cos + sin sin cos c
24.
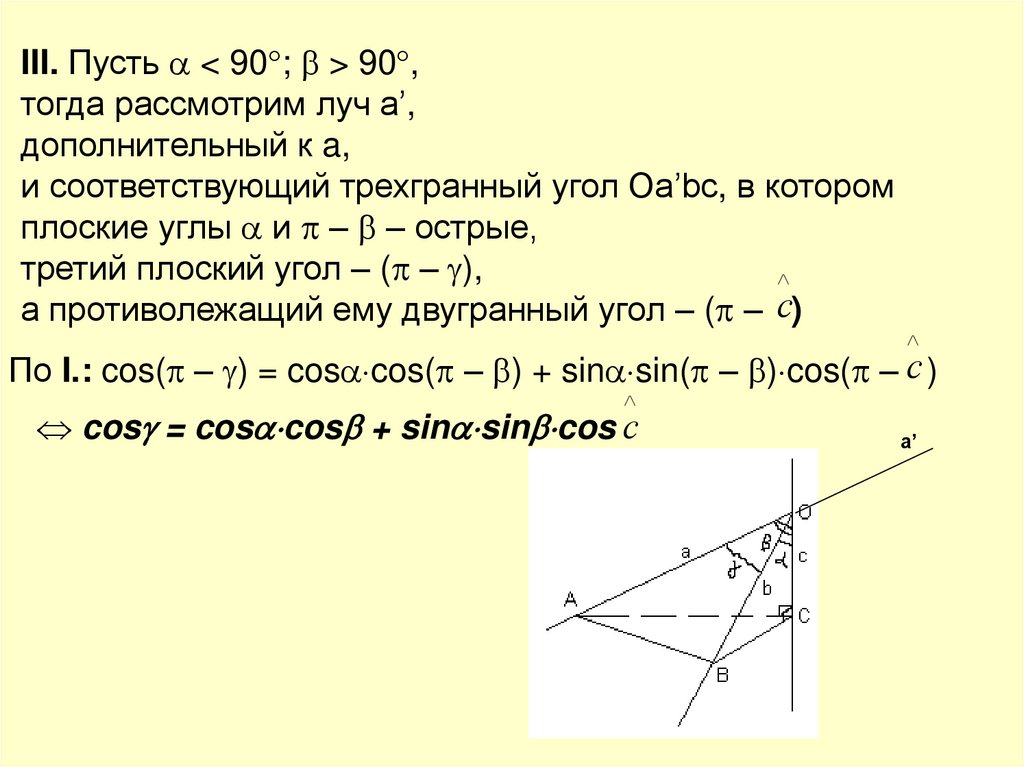
III. Пусть < 90 ; > 90 ,тогда рассмотрим луч a’,
дополнительный к a,
и соответствующий трехгранный угол Оа’bс, в котором
плоские углы и – – острые,
третий плоский угол – ( – ),
а противолежащий ему двугранный угол – ( – c)
По I.: cos( – ) = cos cos( – ) + sin sin( – ) cos( – c )
cos = cos cos + sin sin cos c
a’
25.
IV. Пусть = 90 ; = 90 , тогда = cи равенство, очевидно, выполняется.
Если же только один из этих углов,
например, = 90 ,
то доказанная формула имеет вид:
cos = sin cos c cos = cos(90 – ) cos c
Следствие. Если
c = 90 , то cos = cos cos –
аналог теоремы Пифагора!
26.
,5. Теорема синусов
Многогранный угол, внутренняя область которого
расположена по одну сторону от плоскости каждой из его
граней, называется выпуклым многогранным углом. В
противном случае многогранный угол
называется невыпуклым.
27.
28.
• Многогранник- это тело, поверхностькоторого состоит из конечного числа
плоских многоугольников.
29.
• Грани многогранника - этомногоугольники, которые его
образуют.
• Ребра многогранника - это стороны
многоугольников.
• Вершины многогранника - это
вершины многоугольника.
• Диагональ многогранника - это
отрезок, соединяющий 2 вершины,
не принадлежащие одной грани.
30.
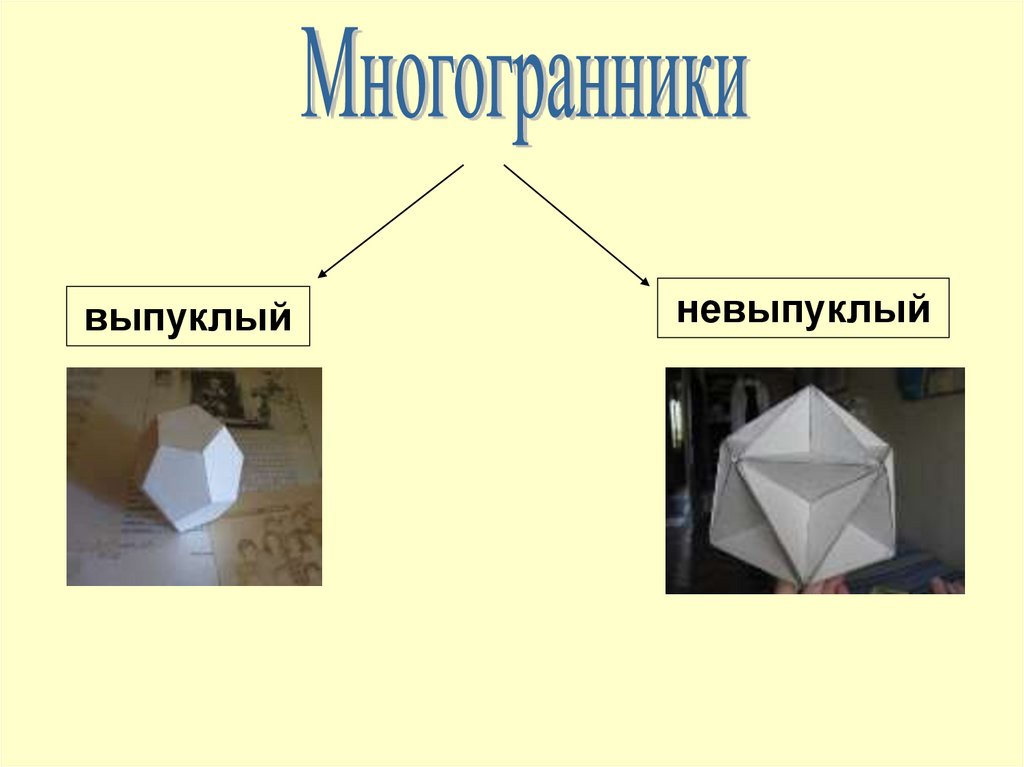
выпуклыйневыпуклый
31.
• Многогранник называется выпуклым, если онрасположен по одну сторону плоскости каждого
многоугольника на его поверхности.
32. Правильные многогранники
• Если грани многогранника являются правильнымимногоугольниками с одним и тем же числом сторон и в
каждой вершине многогранника сходится одно и то же
число ребер, то выпуклый многогранник называется
правильным.
33. Названия многогранников
пришли из Древней Греции,в них указывается число граней:
«эдра» грань;
«тетра»
4;
«гекса»
6;
«окта»
8;
«икоса» 20;
«додека»
12.
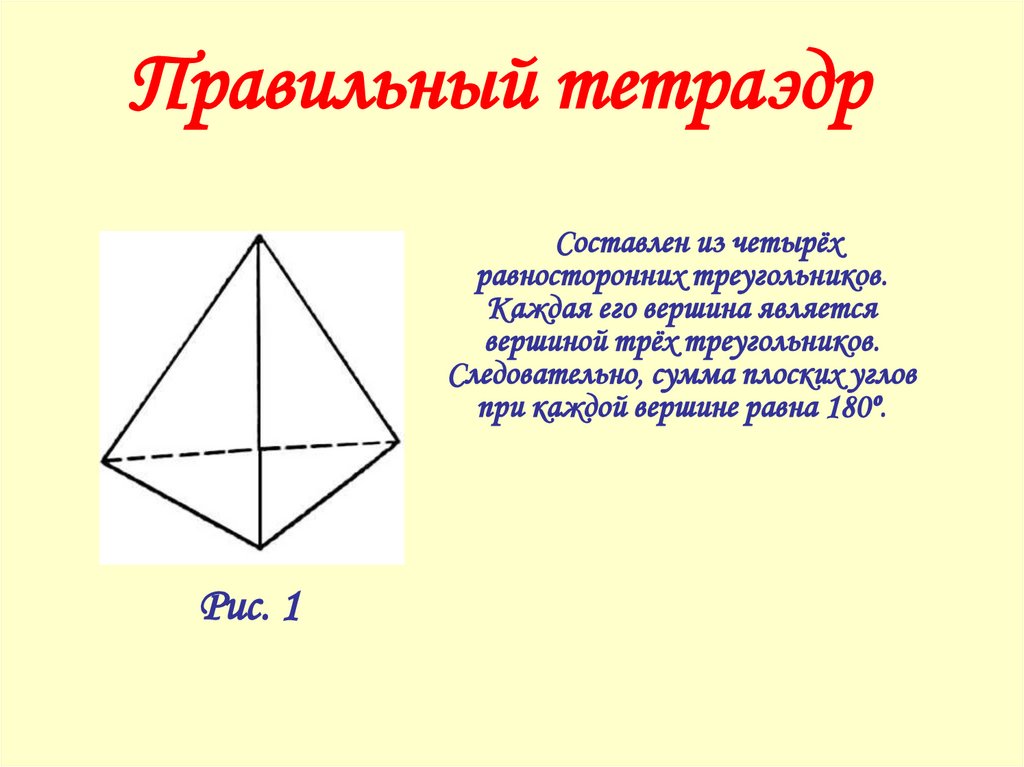
34. Правильный тетраэдр
Составлен из четырёхравносторонних треугольников.
Каждая его вершина является
вершиной трёх треугольников.
Следовательно, сумма плоских углов
при каждой вершине равна 180º.
Рис. 1
35.
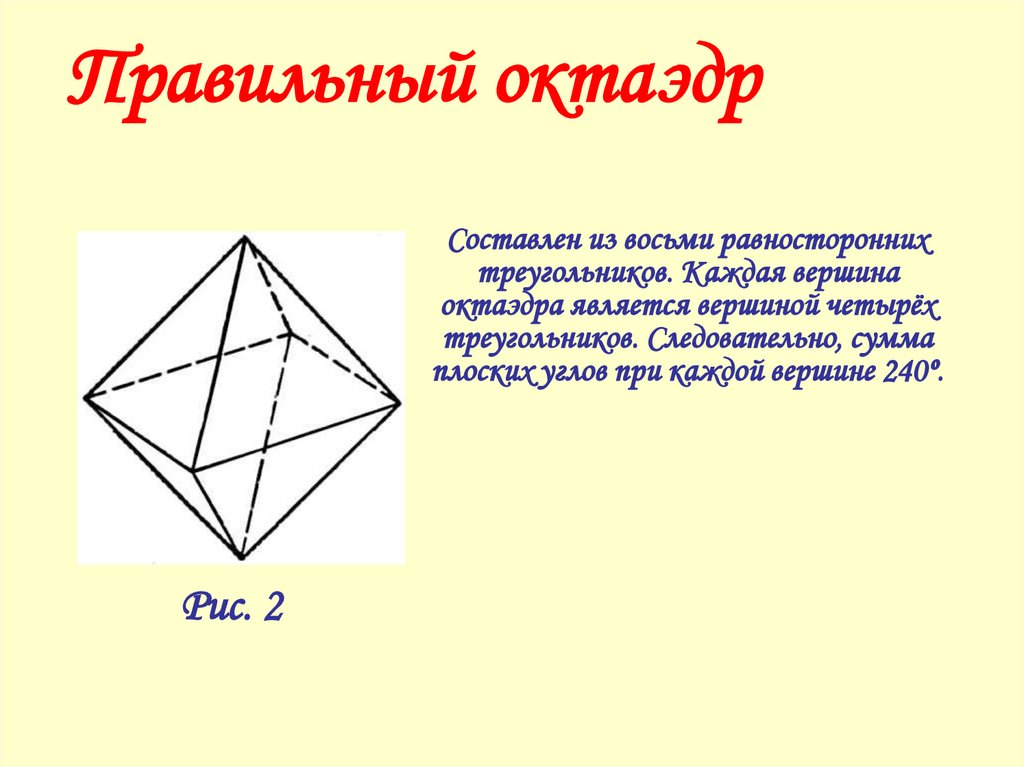
Правильный октаэдрСоставлен из восьми равносторонних
треугольников. Каждая вершина
октаэдра является вершиной четырёх
треугольников. Следовательно, сумма
плоских углов при каждой вершине 240º.
Рис. 2
36.
Правильный икосаэдрСоставлен из двадцати равносторонних
треугольников. Каждая вершина
икосаэдра является вершиной пяти
треугольников. Следовательно, сумма
плоских углов при каждой вершине равна
300º.
Рис. 3
37. Куб (гексаэдр)
Составлен из шестиквадратов. Каждая вершина
куба является вершиной трёх
квадратов. Следовательно,
сумма плоских углов при
каждой вершине равна 270º.
Рис. 4
38.
Правильный додекаэдрСоставлен из двенадцати правильных
пятиугольников. Каждая вершина
додекаэдра является вершиной трёх
правильных пятиугольников.
Следовательно, сумма плоских углов при
каждой вершине равна 324º.
Рис. 5
39.
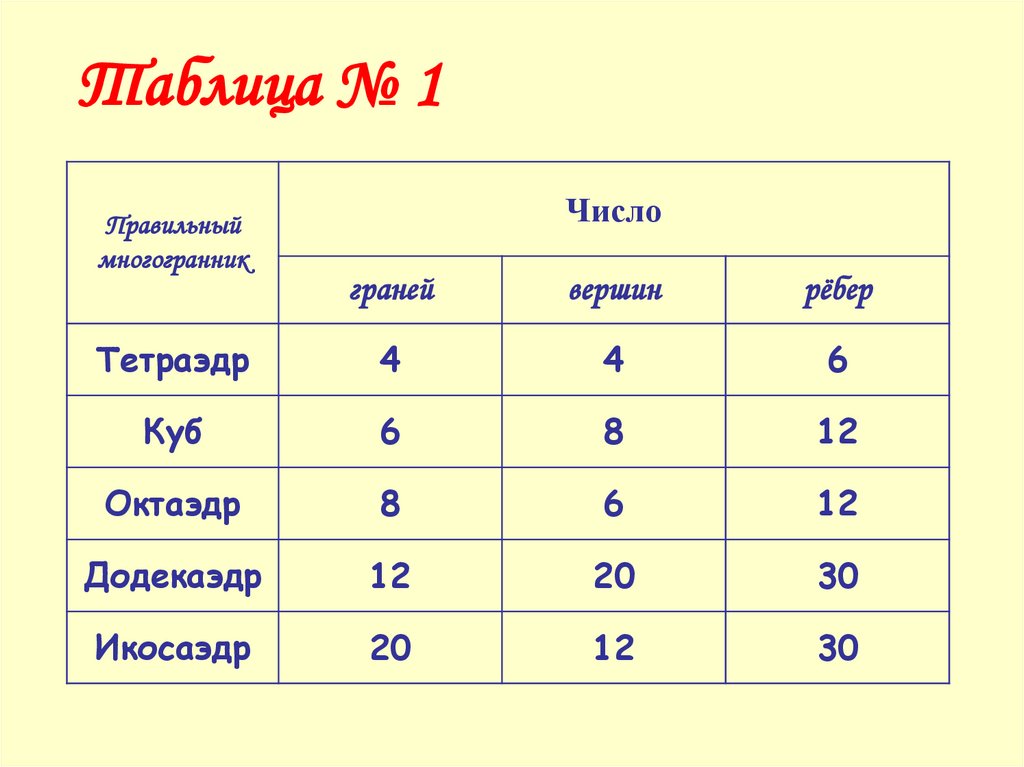
Таблица № 1Правильный
многогранник
Число
граней
вершин
рёбер
Тетраэдр
4
4
6
Куб
6
8
12
Октаэдр
8
6
12
Додекаэдр
12
20
30
Икосаэдр
20
12
30
40.
Формула ЭйлераСумма числа граней и вершин любого многогранника
равна числу рёбер, увеличенному на 2.
Г+В=Р+2
Число граней плюс число вершин минус число рёбер
в любом многограннике равно 2.
Г+В Р=2
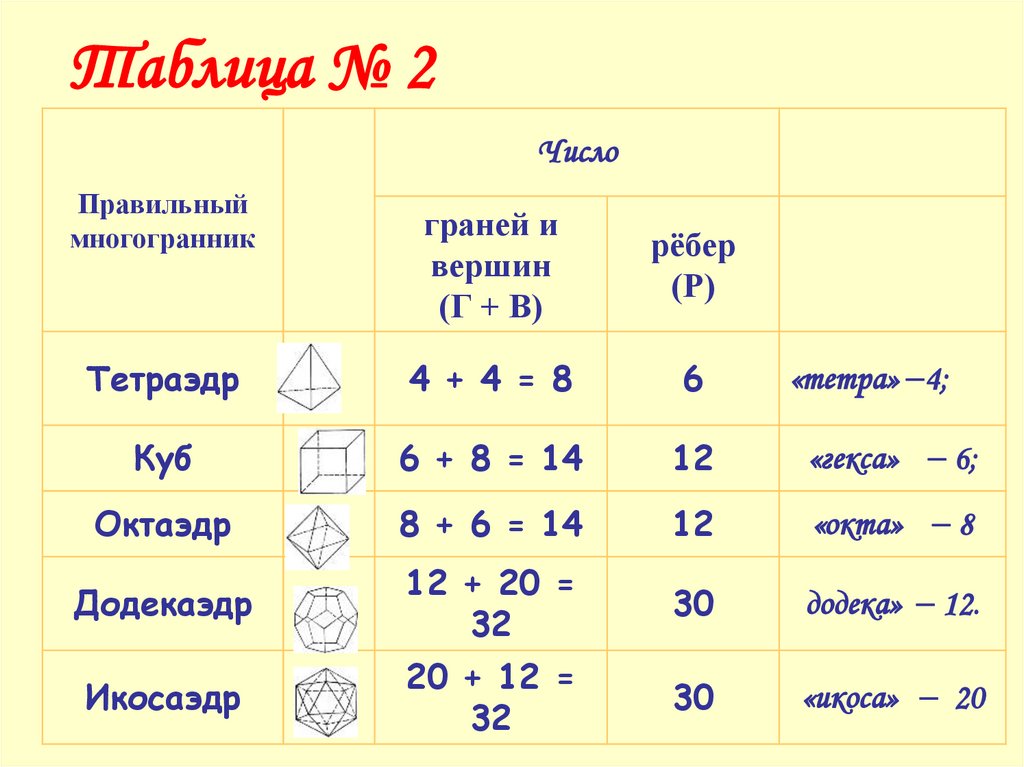
41.
Таблица № 2Число
Правильный
многогранник
граней и
вершин
(Г + В)
рёбер
(Р)
Тетраэдр
4 + 4 = 8
6
Куб
6 + 8 = 14
12
«гекса» 6;
Октаэдр
8 + 6 = 14
12
«окта» 8
Додекаэдр
12 + 20 =
32
30
додека» 12.
Икосаэдр
20 + 12 =
32
30
«икоса» 20
«тетра» 4;


























 Математика
Математика








