Площадь криволинейной трапеции

1. ПЛОЩАДЬ КРИВОЛИНЕЙНОЙ ТРАПЕЦИИ

2. Пусть функция у=f(х) неотрицательна и непрерывна на отрезке [a;b]. Криволинейной трапецией называется фигура, ограниченная

линиями-графиком функции y=f(x), осью Ох, прямыми х=а, х=b.

3.

Составим сумму
S= f(c) ∆x + f(c) ∆x + f(c) ∆x +…+ f(c) ∆x,
где ∆x= x- x.
S = ( f(c) ∆x + f(c) ∆x + f(c) ∆x +…+ f(c) ∆x).
Сумму S называют интегральной суммой.
Площадь криволинейной трапеции,
расположенной:
а) над отрезком [а; b] оси Ох, есть предел
интегральной суммы S, когда max ∆x→ 0;
б) под отрезком [а; b] оси Ох, есть взятый со
знаком «минус» предел интегральной суммы
S, когда max ∆x→ 0;

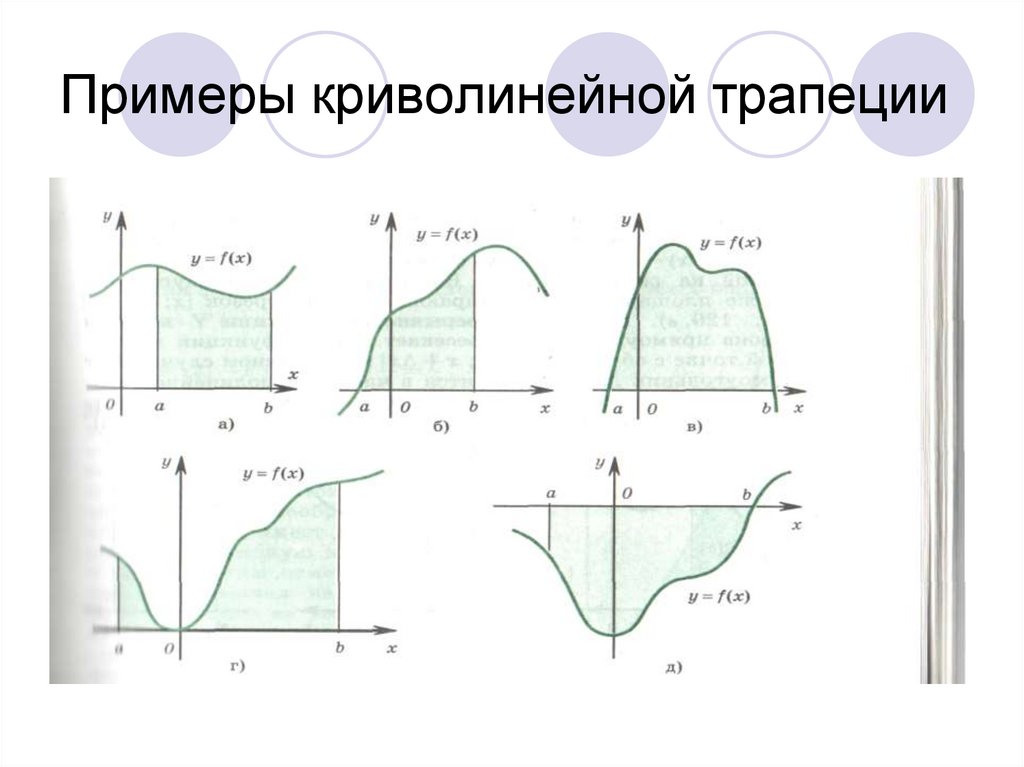
4. Примеры криволинейной трапеции

5. ТЕОРЕМА

Если f – непрерывная и
неотрицательная на отрезке [a; b]
функция, а F – ее первообразная на
этом отрезке, то площадь S
соответствующей криволинейной
трапеции равна приращению
первообразной на отрезке [a; b] , т.е.
S = F(b) – F(a).

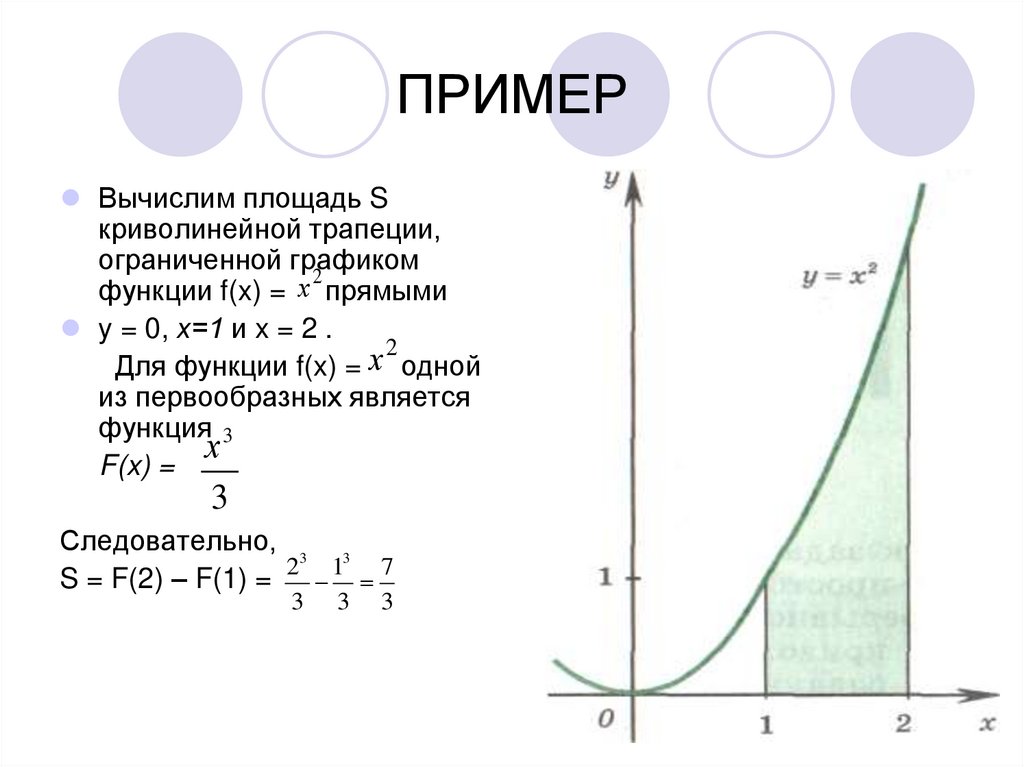
6. ПРИМЕР

Вычислим площадь S
криволинейной трапеции,
ограниченной графиком
2
функции f(x) = х прямыми
y = 0, х=1 и x = 2 .
2
х
Для функции f(x) = одной
из первообразных является
функция 3
х
F(x) =
3
Следовательно, 3 3
S = F(2) – F(1) = 2 1 7
3
3
3
х3
3