Похожие презентации:
Метод координат как универсальный способ решения заданий С-2 ЕГЭ по математике
1. Метод координат как универсальный способ решения заданий С-2 ЕГЭ по математике
2. Общий алгоритм для решения С2 методом координат
1. Ввести прямоугольную систему координат (выбор зависит отобъекта).
2. Выписать координаты всех необходимых точек.
3. Вычислить координаты необходимых векторов.
4. Применить формулу, выполнить вычисления.
5. Записать ответ.
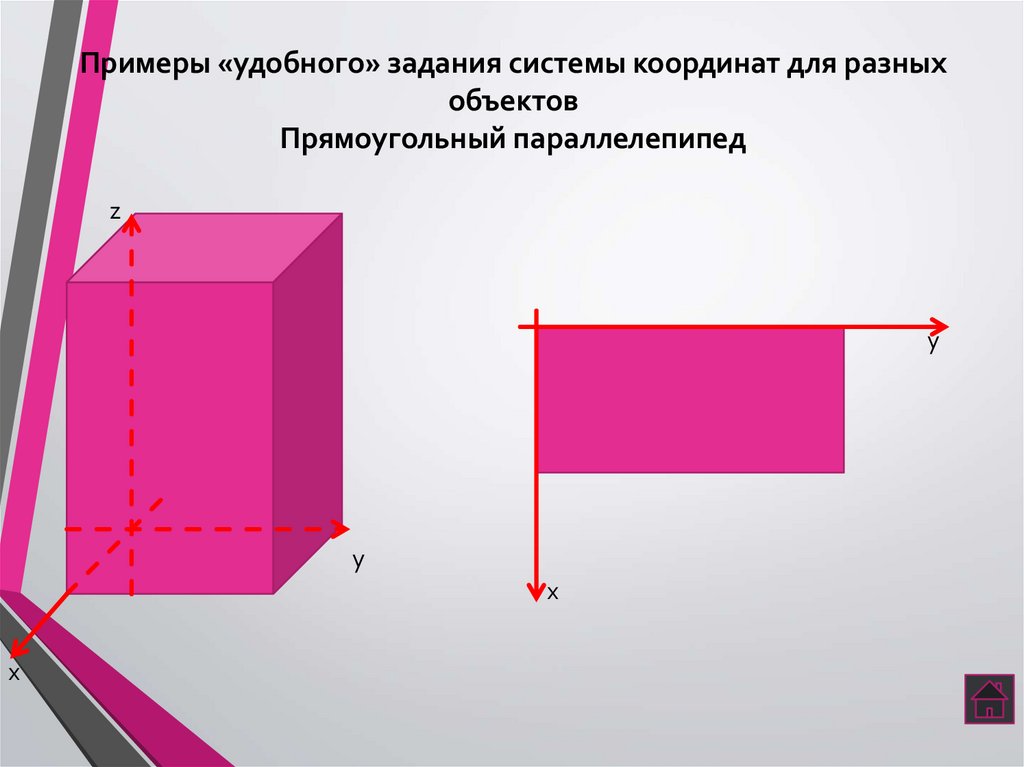
3. Примеры «удобного» задания системы координат для разных объектов Прямоугольный параллелепипед
zy
y
х
х
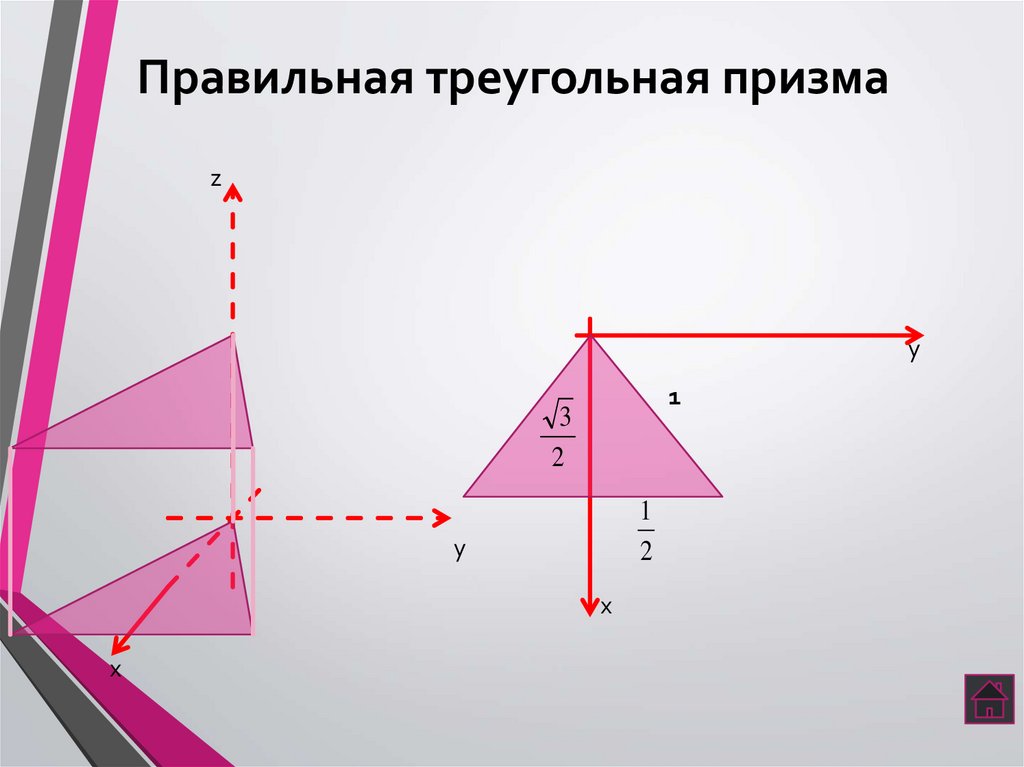
4. Правильная треугольная призма
zy
1
3
2
1
2
y
х
х
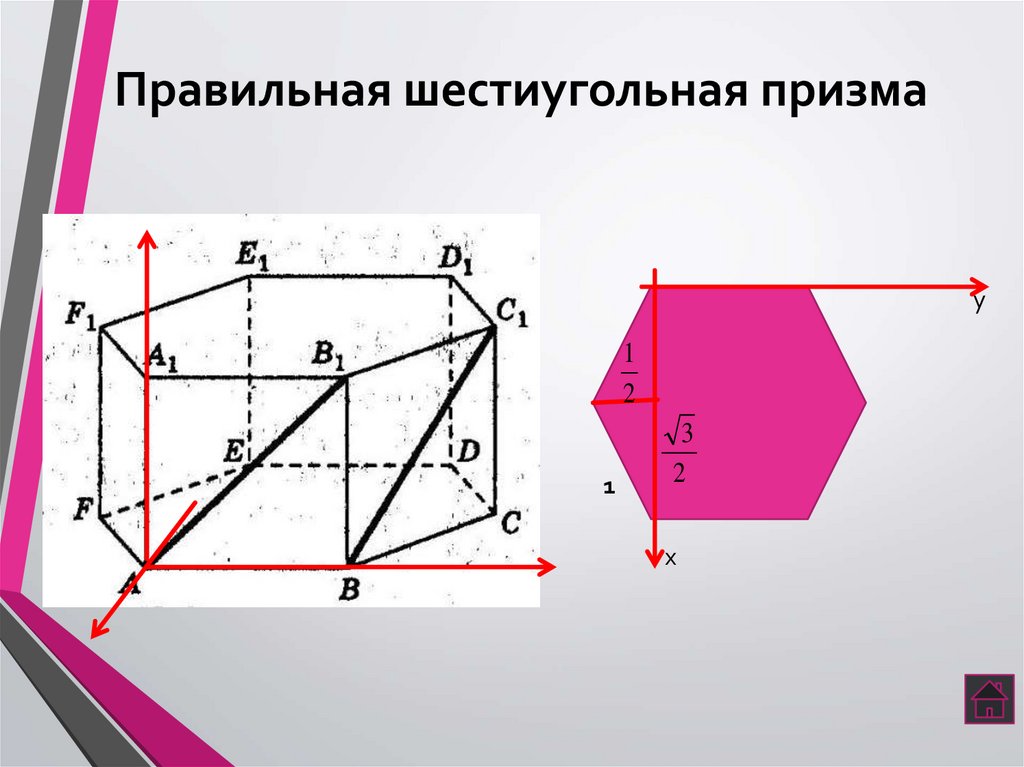
5. Правильная шестиугольная призма
y1
2
1
3
2
х
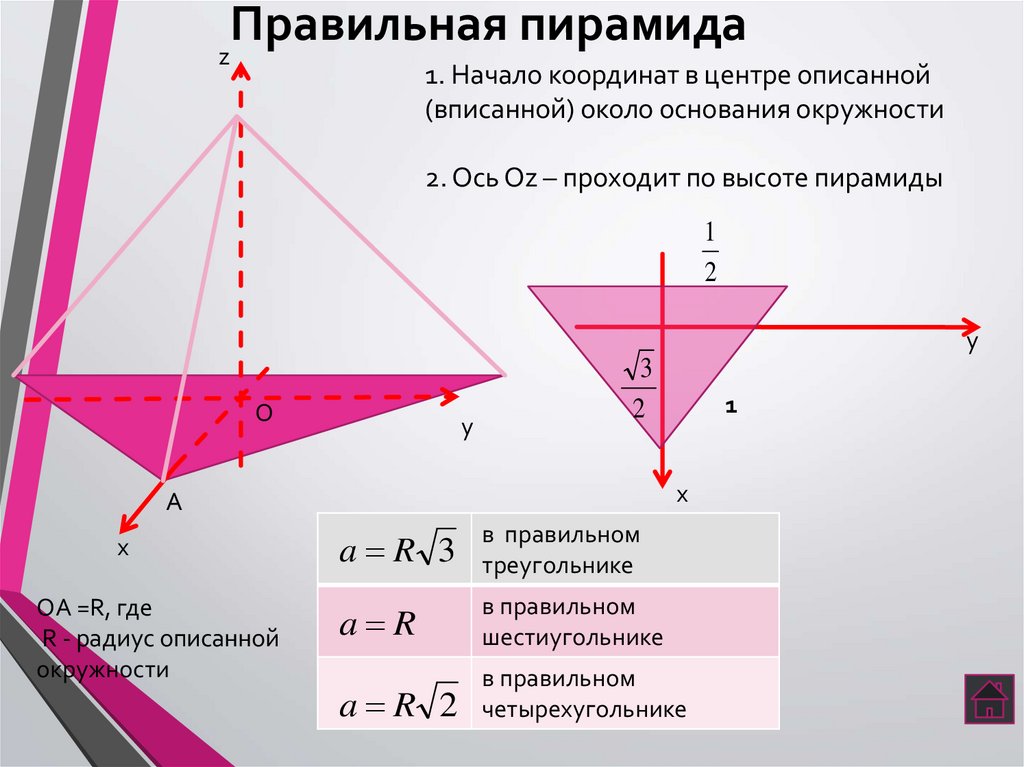
6. Правильная пирамида
z1. Начало координат в центре описанной
(вписанной) около основания окружности
2. Ось Оz – проходит по высоте пирамиды
1
2
y
О
y
3
2
х
А
х
ОА =R, где
R - радиус описанной
окружности
1
a R 3
в правильном
треугольнике
a R
в правильном
шестиугольнике
a R 2
в правильном
четырехугольнике
7. Угол между прямыми (обозначим α)
Используем формулу:cos
| x1 x2 y1 y2 z1 z 2 |
x12 y12 z12 x22 y22 z 22
Где
{x1;y1;z1} – координаты направляющего вектора первой прямой
{x2;y2;z2} – координаты направляющего вектора второй прямой
Так как угол между прямыми выбираем острый,
то косинус положителен
К решению примера 1
К решению примера 2
8.
2. Угол между прямой и плоскостьюα - угол между прямой и плоскостью
β
sin sin( 90 ) cos
β – угол между прямой и перпендикуляром
к плоскости
α
Чтобы найти синус угла между прямой
и плоскостью можно найти косинус угла между
прямой и перпендикуляром к плоскости
9. Уравнение плоскости
(1) aх+by+cz+d=0 – общий вид уравнения плоскостивектор _ n a; b; c плоскости
Через три точки проходит плоскость и притом только одна
Т.к. точки принадлежат плоскости,
то их координаты удовлетворяют уравнению (1)
Составляем и решаем систему уравнений
Находим коэффициенты a, b, c, d
10. Угол между плоскостями
Угол между плоскостями равен углу между перпендикулярами к этим плоскостямa1 x b1 y c1 z d1 0 уравнение _ плоскости _
a2 x b2 y c2 z d 2 0 уравнение _ плоскости _
m a1 ; b1 ; c1
n a2 ; b2 ; c2
cos m;n
a1a2 b1b2 c1c2
a12 b12 c12 a22 b22 c22
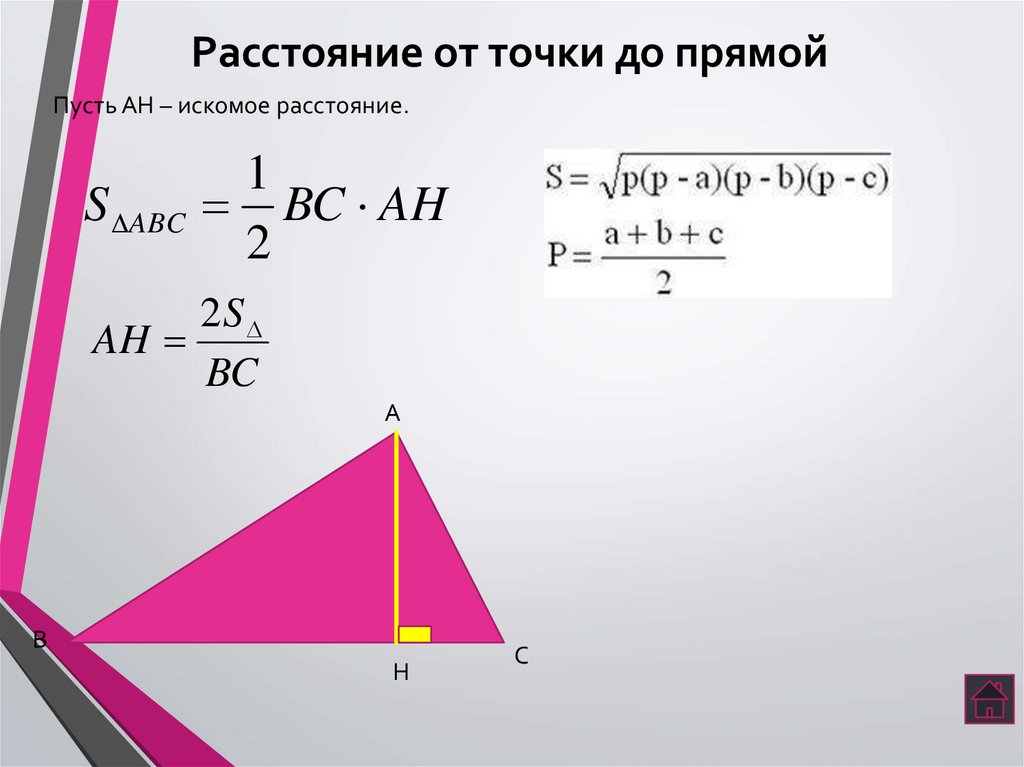
11. Расстояние от точки до прямой
Пусть АН – искомое расстояние.S ABC
1
BC AH
2
2S
AH
BC
А
В
Н
С
12. Расстояние от точки до плоскости
ax0 by0 cz0 da b c
2
2
2
А(х 0,у 0,z 0)
aх+by+cz+d=0
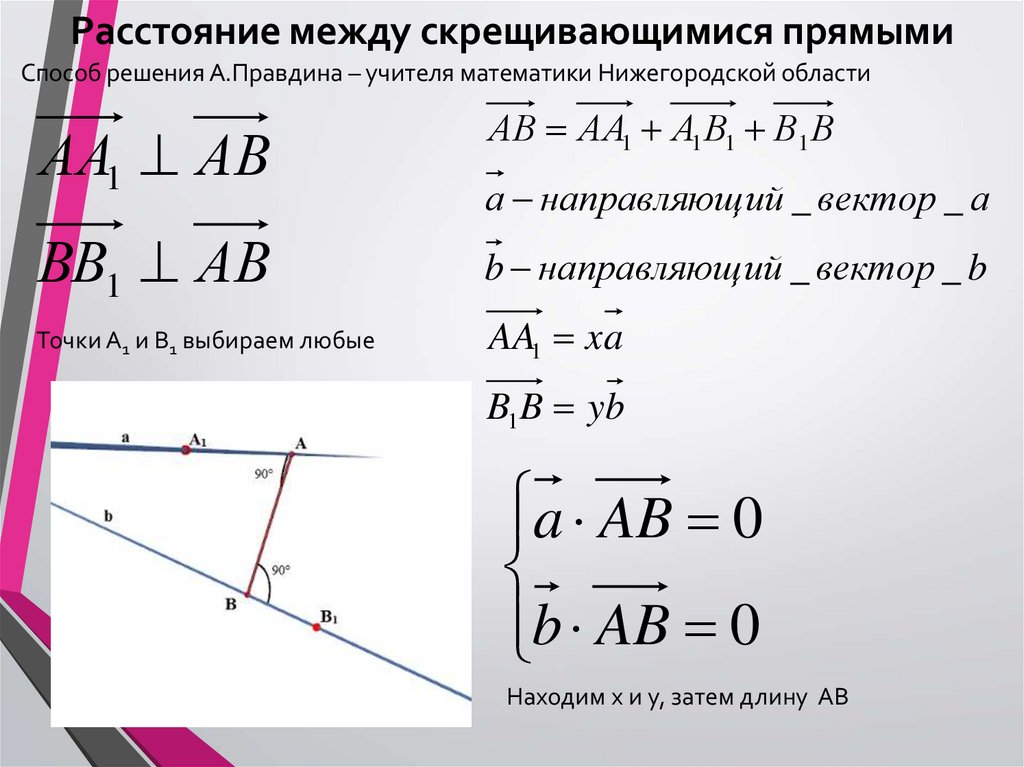
13. Расстояние между скрещивающимися прямыми
Способ решения А.Правдина – учителя математики Нижегородской областиАА1 АВ
АВ АА1 А1 В1 В1 В
а направляющ ий _ вектор _ а
ВВ1 АВ
b направляющ ий _ вектор _ b
Точки А1 и В1 выбираем любые
AA1 x a
B1 B yb
a AB 0
b AB 0
Находим х и у, затем длину АВ







 Математика
Математика








