Линейный гармонический осциллятор

1. Кислицын А.А. Физика атома, атомного ядра и элементарных частиц

12 (2). Линейный гармонический
осциллятор

2.

Гармоническим осциллятором называется частица, совершающая гармонические колебания с частотой ω0.
Потенциальная энергия и частота
равны:
m 02 x 2
f
(12.1)
U
, 0
2
m
где m - масса частицы, x - смещение частицы от положения равновесия, f - возвращающая сила, стремящаяся вернуть частицу в положение равновесия,
пропорциональная смещению и направленная в сторону, противоположную смещению. Поэтому уравнение Шредингера принимает вид:
m 02 x 2
d 2 2m
2 E
0
2
dx
2
(12.2)

3.

Качественно задача подобна рассмотренной выше
задаче о движении частицы в потенциальной яме,
однако здесь имеется особенность, из-за которой
задача довольно сильно усложняется: в пределах
ямы потенциальная энергия не имеет постоянного
значения, а изменяется по параболическому закону. Можно сказать, что частица находится в потенциальной яме, имеющей параболическую форму.
Обозначим для краткости:
m 0
2E
(12.3)
x,
0
Тогда уравнение Шредингера принимает вид:
d m 0
2
0
2
dx
2
(12.4)

4.

Будем искать решение в виде
CH e
(12.5)
2 / 2
где H( ) - неизвестная пока функция, C - константа,
которую на последнем этапе решения определим
из условия нормировки.
Вычислим производные
2 / 2
d
e
2
d d d
dH
С
e / 2 H
d
dx d dx
d
dH
m 0 2 / 2
С
H
e
d
d
dx

5.

2 / 2 d
d
m 0 d dH
С
H e
2
dx
d d
dx
2
2
2 / 2 dH
m 0 d H dH
2 / 2
С
2
H e
H e
d
d
d
m 0 d 2 H
dH
2 2 / 2
С
2 2
H H e
d
d

6.

Подставляем и
d 2 в уравнение (12.4)
dx 2
m 0 d 2 H
dH
2
2 / 2
2
H H e
2
d
d
m 0
2
2 / 2
H e 0
m 0
/ 2
2
сокращаем на C, на e
и на
, раскрываем
скобки, и для функции H получаем следующее
уравнение:
d 2H
dH
2
1 H 0
2
d
d
(12.6)

7.

Будем искать функцию H в виде бесконечного степенного ряда:
2
k
k
(12.7)
H ( ) a a a ... a ... a
0
1
2
k
k 0
k
где a0, a1, a2, ..., an, ... - неизвестные пока постоянные
коэффициенты. Производные от H также надо выразить через бесконечные ряды:
dH
a1 2a2 3a3 2 ... nan n 1 ... nan n 1
d
n 1
(12.8)
d 2H
2
n 2
2
a
3
2
a
4
3
a
...
n
n
1
a
n ...
2
3
4
2
d
n n 1 an n 2
n 2
(12.9)

8.

Подставим формулы (12.7), (12.8), (12.9) в уравнение (12.6):
n 2
n 1
n 0
n 2
n 1
n
n
n
1
a
2
na
1
a
n 0
n
n
или:
n 2
n 1
n 0
n 2
n
n
n
n
1
a
2
na
1
a
n
n n 0
(12.10)
Для того, чтобы левая часть этого уравнения была
равна нулю при любых , необходимо, чтобы
коэффициент при каждой степени был равен
нулю.

9.

a 2 a0
1
2
Запишем эти коэффициенты для нескольких первых
степеней :
0 (свободный член): 2a2 + a0( -1) = 0, или a2 a0 1
2 1
: 3 2a3 - 2a1 + a1( -1) = 0, или a3 a1
3 2
2 : 4 3a4 - 2 2a2 + a2( -1) = 0, или a4 a2 2 2 1
4 3
3 : 5 4a5 - 2 3a3 + a3( -1) = 0, или a5 a3 2 3 1
5 4
2 4 1
4
: 6 5a6 - 2 4a4 + a4( -1) = 0, или a6 a4
6 5
1
2
и т.д.
Нетрудно заметить общую закономерность и записать общее соотношение между коэффициентами:
an 2
2n 1
an
n 2 n 1
(12.11)

10.

Формула (12.11) позволяет последовательно вычислять все члены ряда через предыдущие. Такие соотношения между коэффициентами называются рекуррентными. Т.к. формула (12.11)
позволяет вычислить (n+2)-й коэффициент, если
известен n-й, то можно сказать, что эта формула
определяет два ряда, один из которых состоит
только из членов, имеющих четную степень:
(12.12)
a a 2 a 4 ...
0
2
4
а другой - только нечетную степень:
a1 a3 3 a5 5 ...
(12.13)
Эти ряды представляют собой частные решения
уравнения (12.6).

11.

Оба ряда неограниченно возрастают при больших
значениях , и, значит, вообще говоря, не удовлетворяют условию ограниченности решения. Однако
можно заметить, что если какой-то коэффициент
an окажется равным нулю, то все остальные коэффициенты с большими номерами также будут равны нулю. Другими словами, при некоторых избранных значениях параметра ряды "обрываются" на
некотором значении n, т.е. из бесконечных рядов
превращаются в полиномы конечной степени (они
называются полиномами Чебышева-Эрмита). В
этом случае множитель e /,2 входящий в формулу
(12.5), обеспечивает ограниченность функции
2
n Сn H n ( )e
2 / 2

12.

Итак, для того, чтобы решение при больших не обращалось в бесконечность, надо коэффициенты
степенного ряда подобрать так, чтобы они были
равны нулю, начиная с некоторого номера n+1. Как
видно из формулы (12.11), для того, чтобы an 0, а
an+2 = 0, необходимо, чтобы параметр принимал
дискретные значения
n = 2n + 1.
(12.14)
Отсюда и из формулы (12.3) находим собственные
значения энергии осциллятора:
1
En 0 n ,
2
n 0, 1, 2, 3,...
(12.15)

13.

В частности, при n = 0 минимальная энергия осциллятора не равна нулю:
E0
0
2
(12.16)
что согласуется с соотношениями неопределенности. Действительно, если бы частица покоилась,
она одновременно имела бы определенную координату и определенное (нулевое) значение импульса, что противоречит соотношению неопределенностей. Энергия E0 называется "нулевой
энергией осциллятора"; она не исчезает, даже
когда температура стремится к абсолютному
нулю.

14.

Найдем общий вид полиномов Чебышева-Эрмита.
Для этого с помощью формулы (12.11) с учетом
условия (12.14) запишем соотношение между
коэффициентами an и an-2:
2(n 2) 1 2n 1
4
an an 2
an 2
n n 1
n n 1
отсюда
an 2
n(n 1)
n(n 1)
an
an
2
4
1 2
Выполняя аналогичные действия, найдем соотношение между коэффициентами an, an-2 и an-4:
an 4
(n 2)(n 3)
n(n 1)(n 2)( n 3)
an 2
an
2
1 2 2
1 2 24

15.

Поэтому искомый полином степени n имеет вид:
n n(n 1) n 2 n(n 1)(n 2)(n 3) n 4
H n ( ) an
...
2
4
1 2
1 2 2
или
n / 2
n!
k
H n ( ) an
( 1) 2 k
n 2 k (12.17)
k 0
2 k !(n 2k )!
В этой формуле верхний предел суммирования,
обозначенный как [n/2], равен целой части от
деления n на 2, т.е. если n - четное число, то
верхний предел суммирования равен n/2, а если n
- нечетное число, то (n-1)/2. Напомним также, что
по определению 0! = 1.

16.

Полученные таким образом полиномы определены с
точностью до постоянного множителя an (коэффициента при старшем члене). Принято этот коэффициент положить равным 2n, тогда все коэффициенты в полиноме Чебышева-Эрмита любой степени
будут целыми числами. Запишем в качестве примера несколько первых полиномов Чебышева-Эрмита:
H0( ) = 1
H1( ) = 2
H2( ) = 4 2 - 2
H3( ) = 8 3 - 12
H4( ) = 16 4 - 48 2 + 12
H5( ) = 32 5 - 160 3 + 120
H6( ) = 64 6 - 480 4 + 720 2 - 120
H7( ) = 128 7 - 1344 5 + 3360 3 - 1680

17.

Непосредственной проверкой легко убедиться, что полученные полиномы действительно являются решениями уравнения (12.6),
которое с учетом равенства n = 2n + 1 можно записать в виде:
H 2 H 2n H 0
(12.18)
Например, для n = 2:
2
H 2 4 2, H 2 8 , H 2 8
Подставляя в (12.17), получаем тождество:
8 2 8 2 2 4 2 2 0

18.

Отметим еще некоторые важные свойства полиномов Чебышева-Эрмита.
Полином любой степени n > 0 можно вычислить по
формуле:
n
2
)
n 2 d (e
(12.19)
H n ( ) ( 1) e
n
d
Например, при n = 1:
2
d 2
H1 ( ) e
e
2
d
при n = 2:
2
d
2
2 d
2
H 2 ( ) e
e
e
2 e
4 2
2
d
d
2
и т.д.

19.

Полином любой степени можно определить по рекуррентной формуле
H n 1 ( ) 2 H n ( ) 2nH n 1 ( )
если известны два предыдущих. Например, полагая n = 7, и используя приведенные выше формулы для H6 и H7, найдем H8:
H 8 2 H 7 2 7 H 6
256 8 2688 6 6720 4 3360 2
14 64 6 480 4 720 2 120
256 8 3584 6 13440 4 13440 2 1680

20.

Собственные функции линейного осциллятора ортогональны в промежутке от -∞ до +∞, т.е.:
d 0
n
m
если n m
Если n = m, то получаем условие нормировки, которое позволяет найти коэффициенты Cn:
dx 1 C
2
n
2
n
e
2
H n2 ( )d
Используя формулу (12.19) и интегрируя по частям,
получаем следующий результат:
1
m 0
Cn
2n n !
(12.20)

21.

В частности, для нулевого состояния нормировочный множитель равен
C0
4
m 0
Таким образом, собственная функция нулевого состояния имеет вид:
0 ( x ) C0 e / 2 H 0
2
4
m 0
m 0 x 2
exp
(12.21)
2
а соответствующая плотность вероятности равна:
2 ( x ) C02 e H 02
2
0
m 0
m 0 x 2
exp
(12.22)

22.

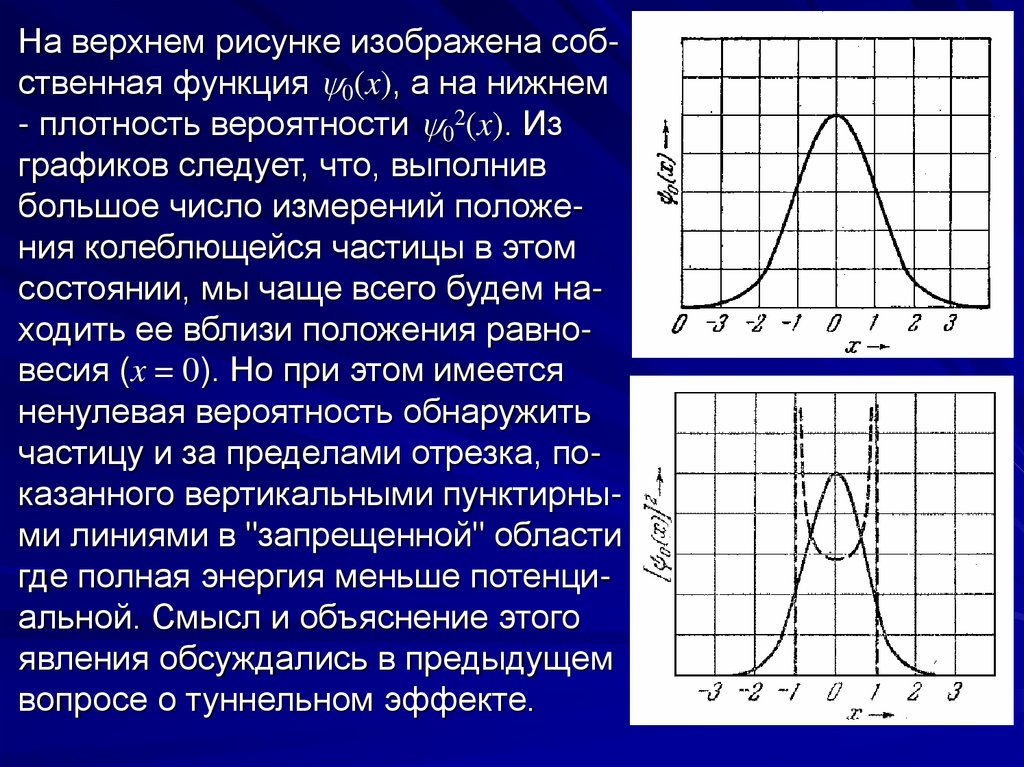
На верхнем рисунке изображена собственная функция 0(x), а на нижнем
- плотность вероятности 02(x). Из
графиков следует, что, выполнив
большое число измерений положения колеблющейся частицы в этом
состоянии, мы чаще всего будем находить ее вблизи положения равновесия (x = 0). Но при этом имеется
ненулевая вероятность обнаружить
частицу и за пределами отрезка, показанного вертикальными пунктирными линиями в "запрещенной" области
где полная энергия меньше потенциальной. Смысл и объяснение этого
явления обсуждались в предыдущем
вопросе о туннельном эффекте.

23.

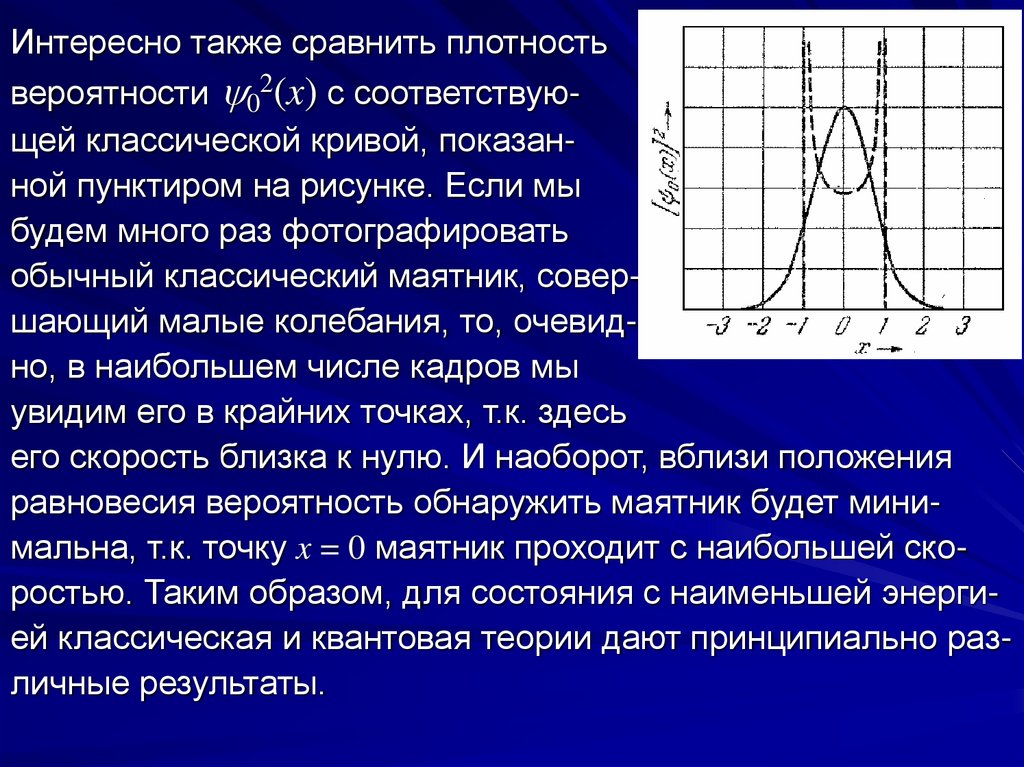
Интересно также сравнить плотность
вероятности 02(x) с соответствующей классической кривой, показанной пунктиром на рисунке. Если мы
будем много раз фотографировать
обычный классический маятник, совершающий малые колебания, то, очевидно, в наибольшем числе кадров мы
увидим его в крайних точках, т.к. здесь
его скорость близка к нулю. И наоборот, вблизи положения
равновесия вероятность обнаружить маятник будет минимальна, т.к. точку x = 0 маятник проходит с наибольшей скоростью. Таким образом, для состояния с наименьшей энергией классическая и квантовая теории дают принципиально различные результаты.

24.

Теперь рассмотрим возбужденные состояния осциллятора с n = 1, 2, 3, .... На рисунке изображены собственные функции первых из этих
состояний 1(x)- 6(x). Как и
следовало ожидать, эти
функции представляют собой что-то вроде стоячих волн и качественно похожи
на аналогичные кривые, полученные выше при решении задачи о частице в прямоугольной потенциальной яме. При n = 1 имеется один узел внутри параболической ямы (в центре ямы); при n = 2 - два таких узла, при n = 3 - три узла и т.д.

25.

Здесь изображены плотности вероятности 12(x), 22(x),
32(x), 42(x) возбужденных
состояний осциллятора с
n = 1, 2, 3, 4 .... Легко заметить, что с увеличением числа n вероятность обнаружения частицы вблизи центра
ямы постепенно уменьшается, а вблизи краев - растет. Т.е. при малых значениях n квантовый осциллятор ведет себя совершенно не так, как классический,
но с увеличением n квантовое распределение плотности вероятности постепенно приближается к классическому.

26.

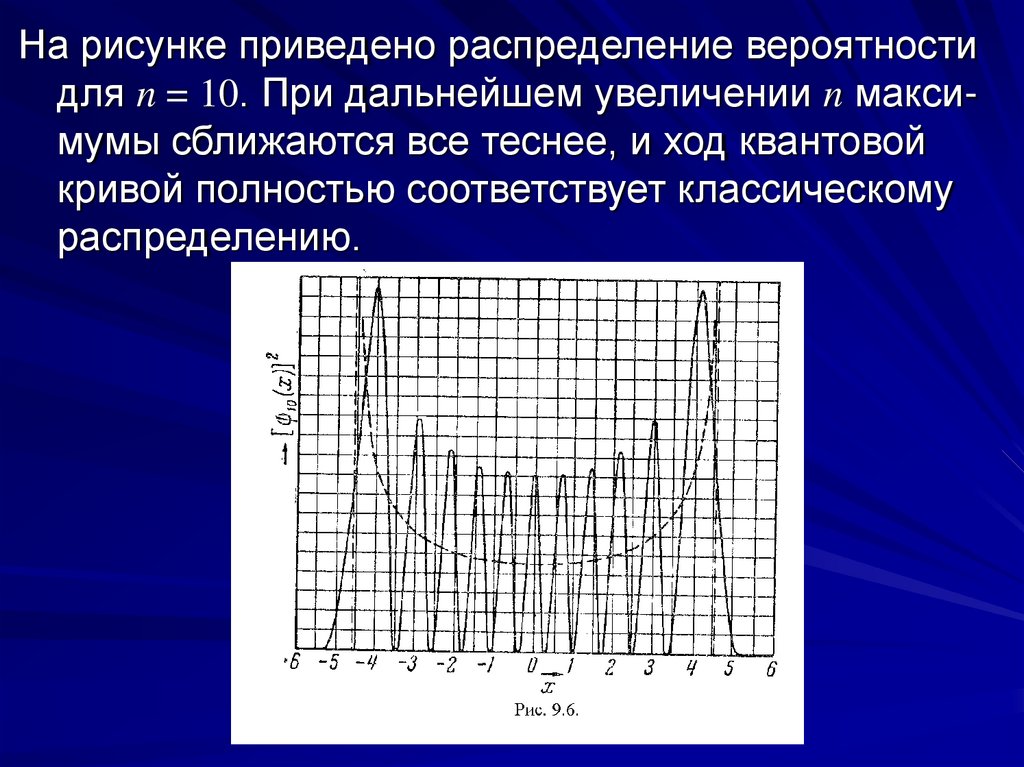
На рисунке приведено распределение вероятности
для n = 10. При дальнейшем увеличении n максимумы сближаются все теснее, и ход квантовой
кривой полностью соответствует классическому
распределению.