Теоремы. Доказательство теоремы

1.

ДЗ по геометрии:
1) выполнить задания (слайд 2-3);
2) записать в тетрадь теоремы 1-2 и доказательства к ним;
3) выучить доказательство теоремы 1

2.

2)
60 60
6)
1)
8)
3)
7)
4)
9)
11)
5)
13)
10)
12)
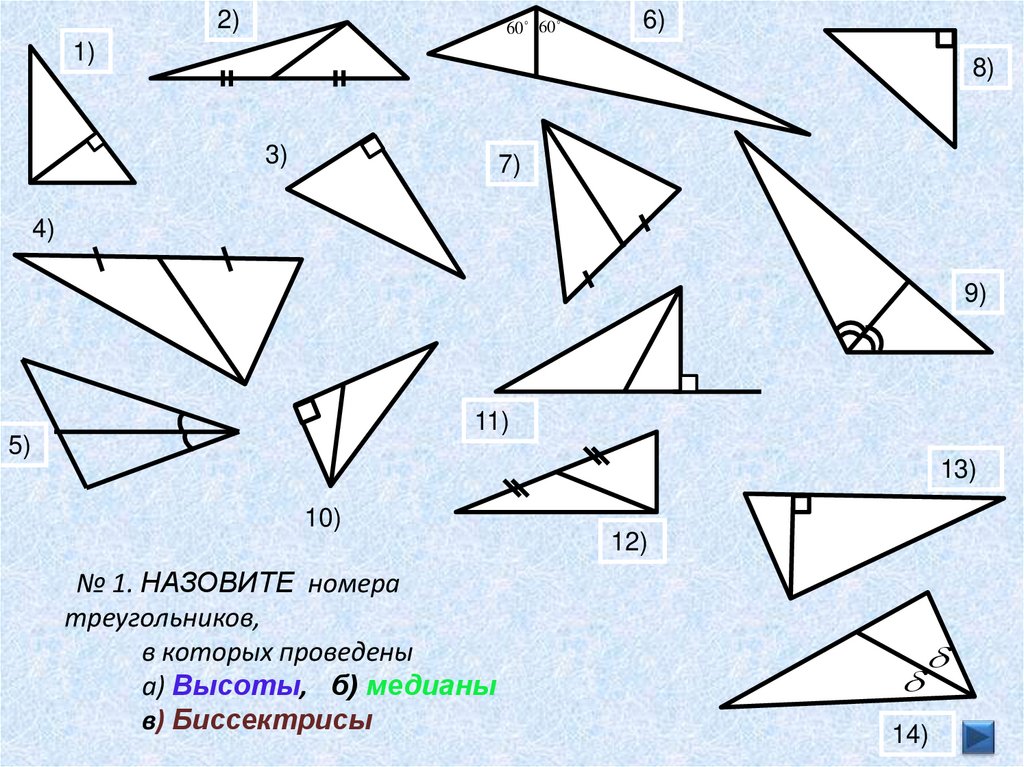
№ 1. НАЗОВИТЕ номера
треугольников,
в которых проведены
а) Высоты, б) медианы
в) Биссектрисы
14)

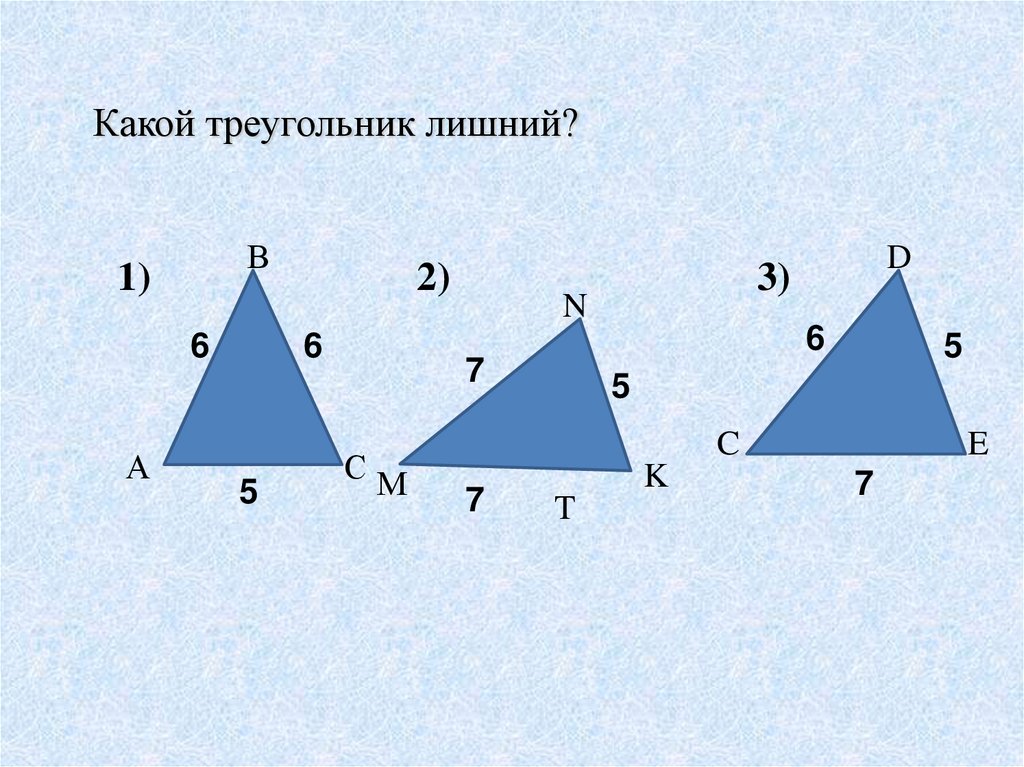
3. Какой треугольник лишний?

В
1)
6
А
2)
3)
N
6
6
5
D
7
СМ
5
5
C
7
K
T
E
7

4.

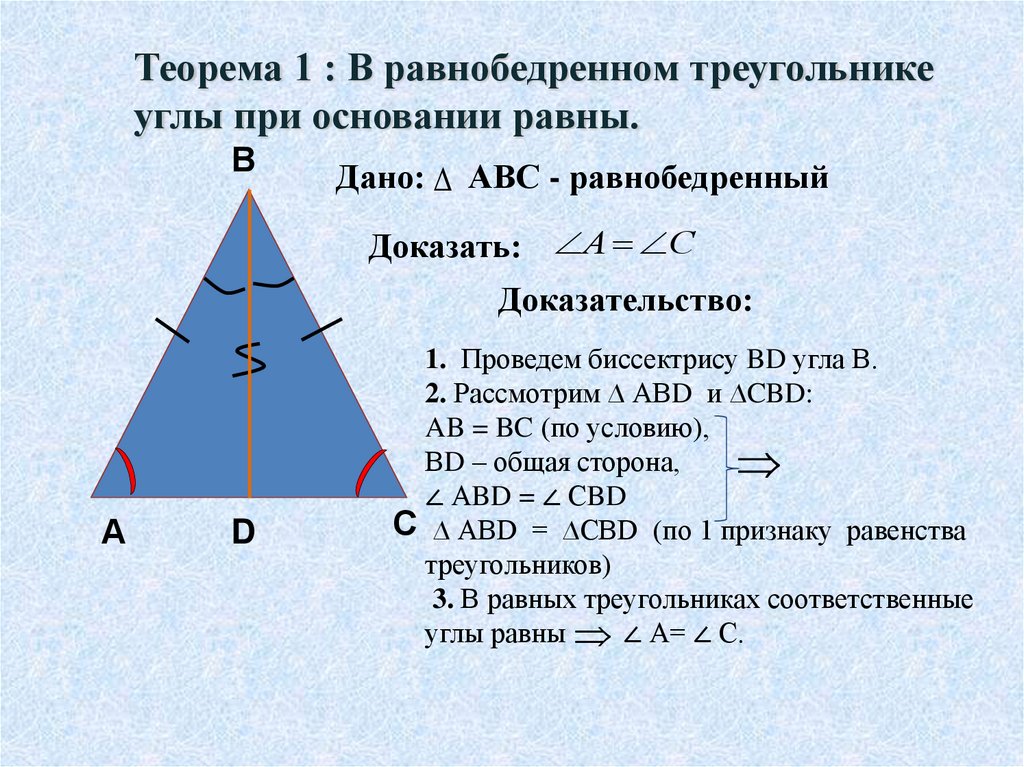
Теорема 1 : В равнобедренном треугольнике
углы при основании равны.
В
Дано: АВС - равнобедренный
Доказать: А С
Доказательство:
1. Проведем биссектрису BD угла В.
2. Рассмотрим ∆ АВD и ∆CBD:
AB = BC (по условию),
ВD – общая сторона,
∠ АBD = ∠ СBD
С ∆ АВD = ∆CBD (по 1 признаку равенства
треугольников)
3. В равных треугольниках соответственные
углы равны ∠ А= ∠ С.
А
D

5.

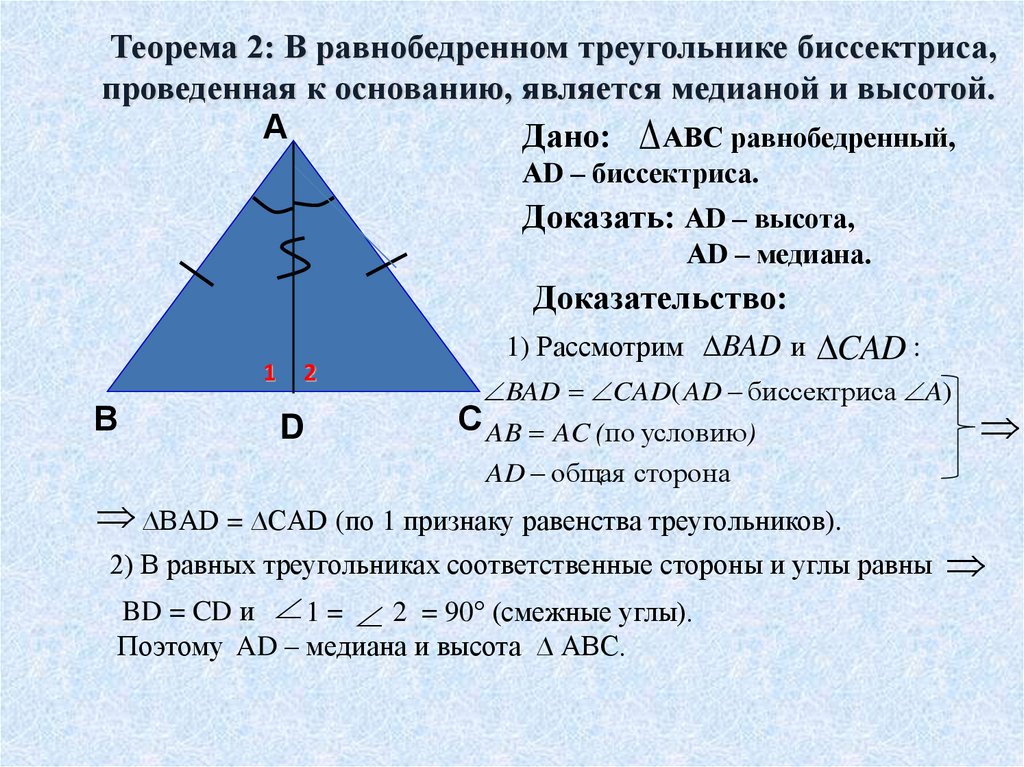
Теорема 2: В равнобедренном треугольнике биссектриса,
проведенная к основанию, является медианой и высотой.
А
Дано: АВС равнобедренный,
АD – биссектриса.
Доказать: АD – высота,
АD – медиана.
Доказательство:
1
В
2
D
1) Рассмотрим BAD и
CAD :
BAD CAD( AD биссектриса A)
С AB AC (по условию)
AD общая сторона
∆BAD = ∆CAD (по 1 признаку равенства треугольников).
2) В равных треугольниках соответственные стороны и углы равны
BD = CD и 1 = 2 = 90° (смежные углы).
Поэтому AD – медиана и высота ∆ АВС.