Похожие презентации:
Свойства равнобедренного треугольника
1.
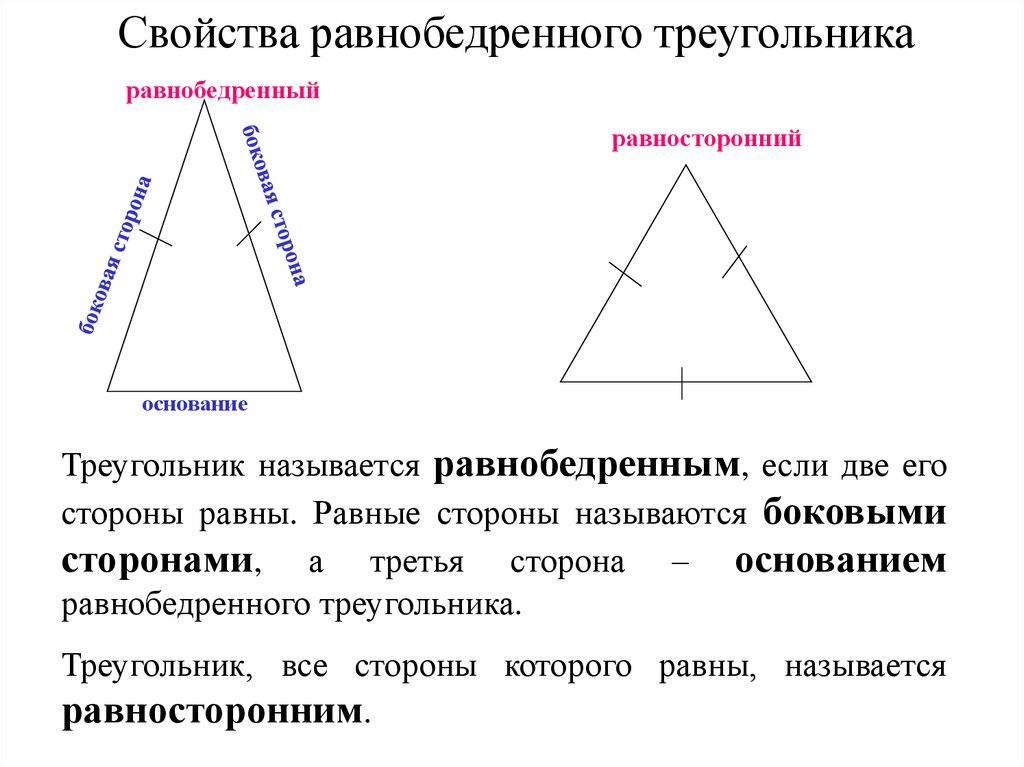
Свойства равнобедренного треугольникаравнобедренный
равносторонний
основание
Треугольник называется равнобедренным, если две его
стороны равны. Равные стороны называются боковыми
сторонами, а третья сторона – основанием
равнобедренного треугольника.
Треугольник, все стороны которого равны, называется
равносторонним.
2.
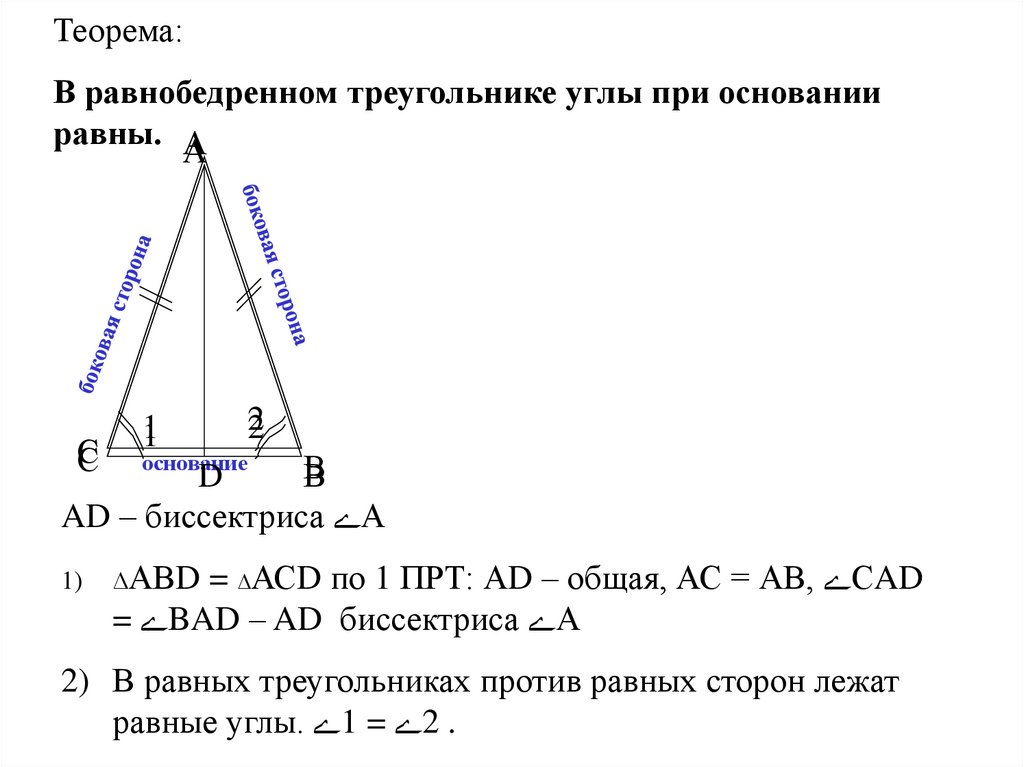
Теорема:В равнобедренном треугольнике углы при основании
равны. А
А
С
С
11
22
В
D
В
AD – биссектриса А
1)
основание
∆АВD
= ∆АСD по 1 ПРТ: АD – общая, АС = АВ, СAD
= BAD – AD биссектриса А
2) В равных треугольниках против равных сторон лежат
равные углы. 1 = 2 .
3.
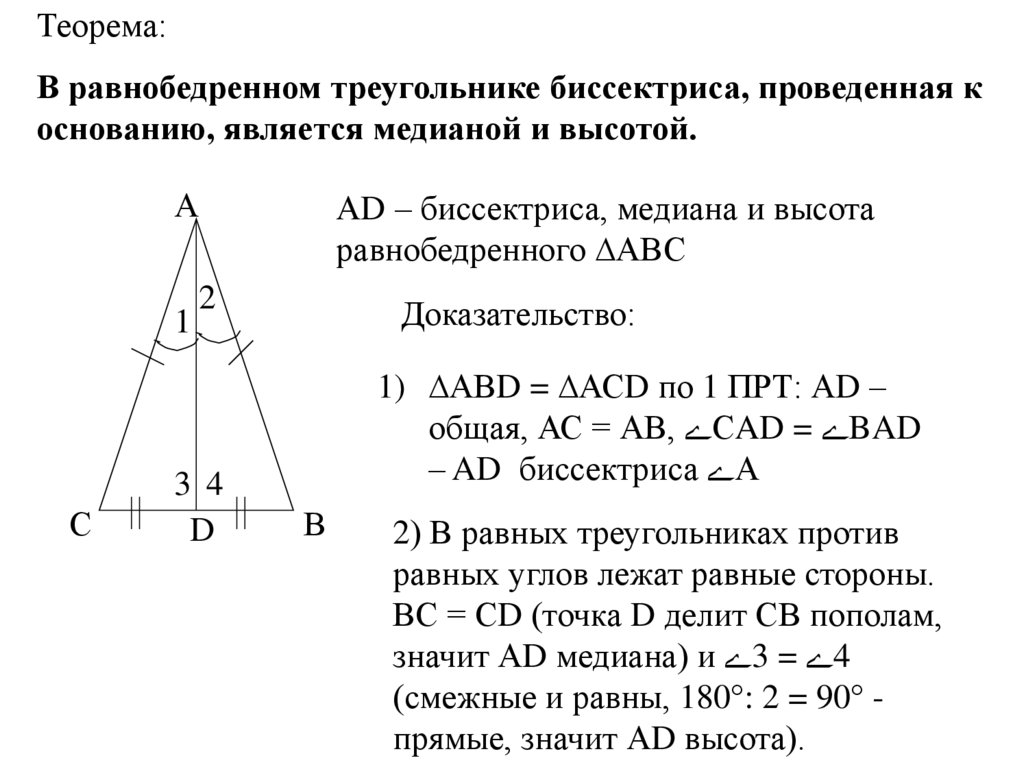
Теорема:В равнобедренном треугольнике биссектриса, проведенная к
основанию, является медианой и высотой.
А
1
С
АD – биссектриса, медиана и высота
равнобедренного ∆АВС
2
3 4
D
Доказательство:
1) ∆АВD = ∆АСD по 1 ПРТ: АD –
общая, АС = АВ, СAD = BAD
– AD биссектриса А
В
2) В равных треугольниках против
равных углов лежат равные стороны.
ВС = СD (точка D делит СВ пополам,
значит АD медиана) и 3 = 4
(смежные и равны, 180°: 2 = 90° прямые, значит АD высота).
4.
Верны утверждения:1. Высота равнобедренного ∆-ка, проведенная к основанию,
является медианой и биссектрисой.
2. Медиана равнобедренного ∆-ка, проведенная к основанию,
является высотой и биссектрисой.

 Математика
Математика








