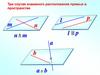
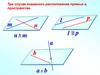
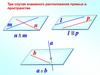
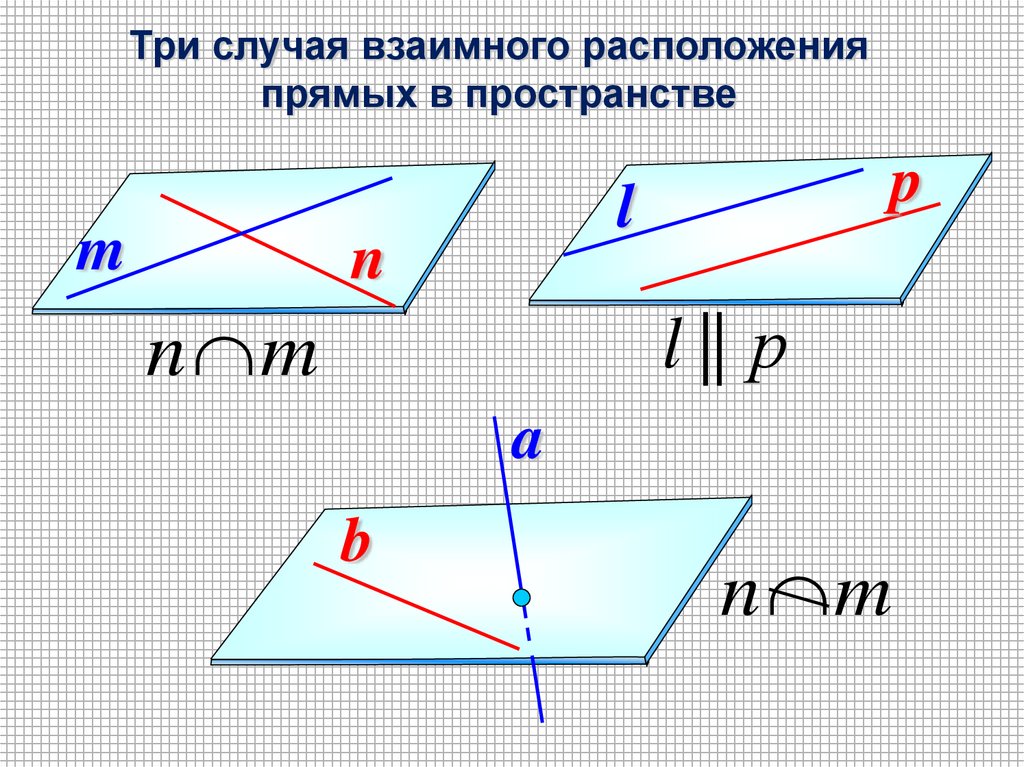
Три случая взаимного расположения прямых в пространстве

1.

Три случая взаимного расположения
прямых в пространстве
m
p
l
n
l || р
n m
a
b
n m

2.

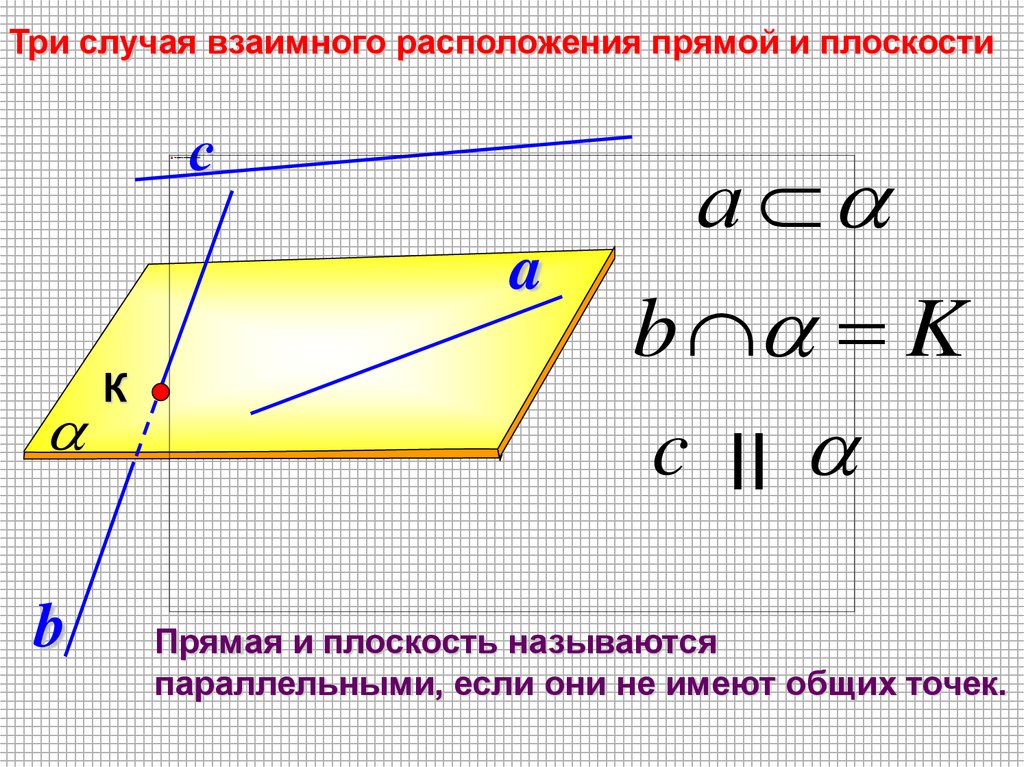
Три случая взаимного расположения прямой и плоскости
с
a
b
К
а
b K
c II
Прямая и плоскость называются
параллельными, если они не имеют общих точек.

3. 28.09.20 г.

Параллельность
прямой и плоскости.

4.

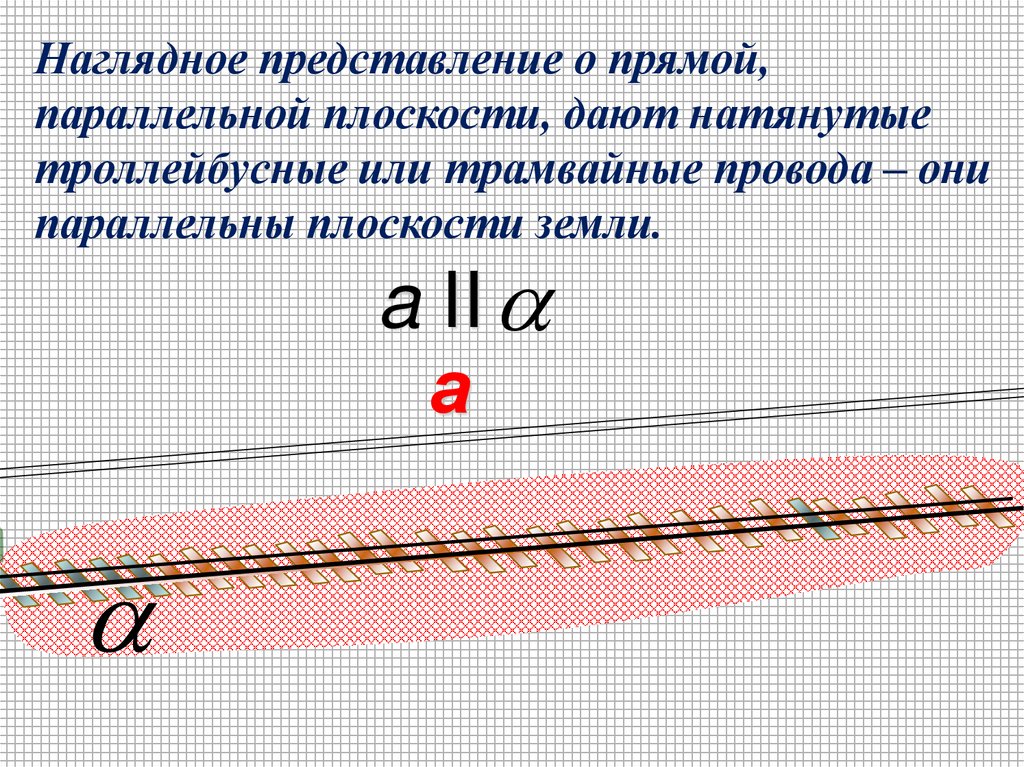
Наглядное представление о прямой,
параллельной плоскости, дают натянутые
троллейбусные или трамвайные провода – они
параллельны плоскости земли.
a II
а

5.

а

6.

а
b

7.

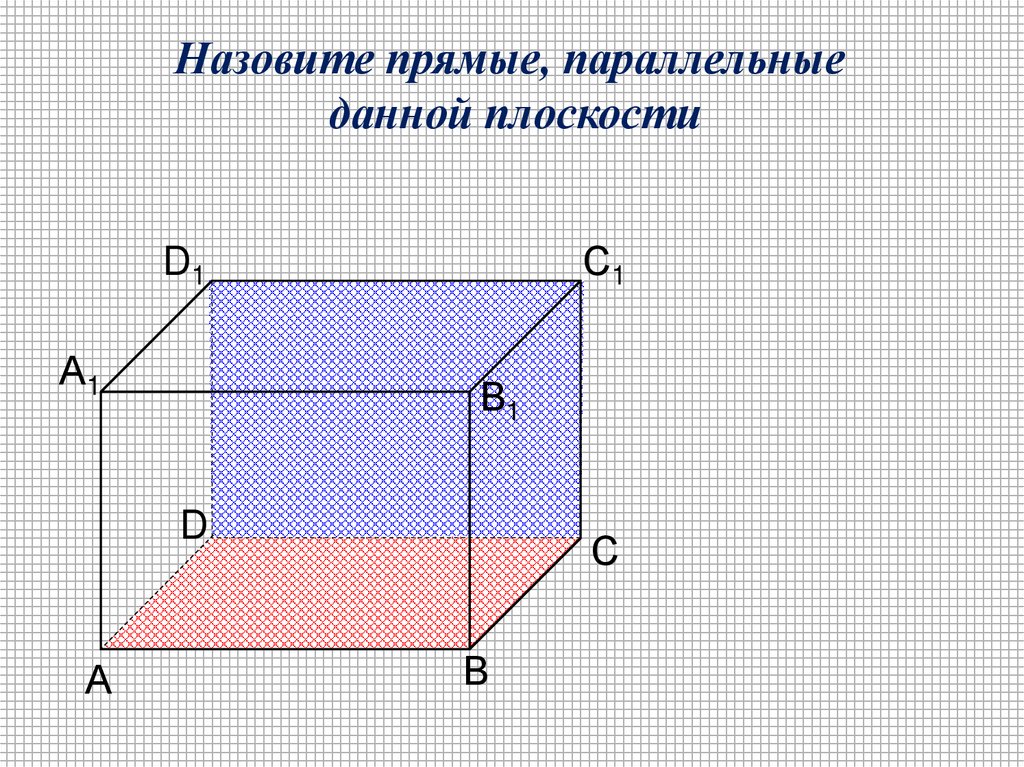
Назовите прямые, параллельные
данной плоскости
С1
D1
А1
В1
D
А
С
В

8.

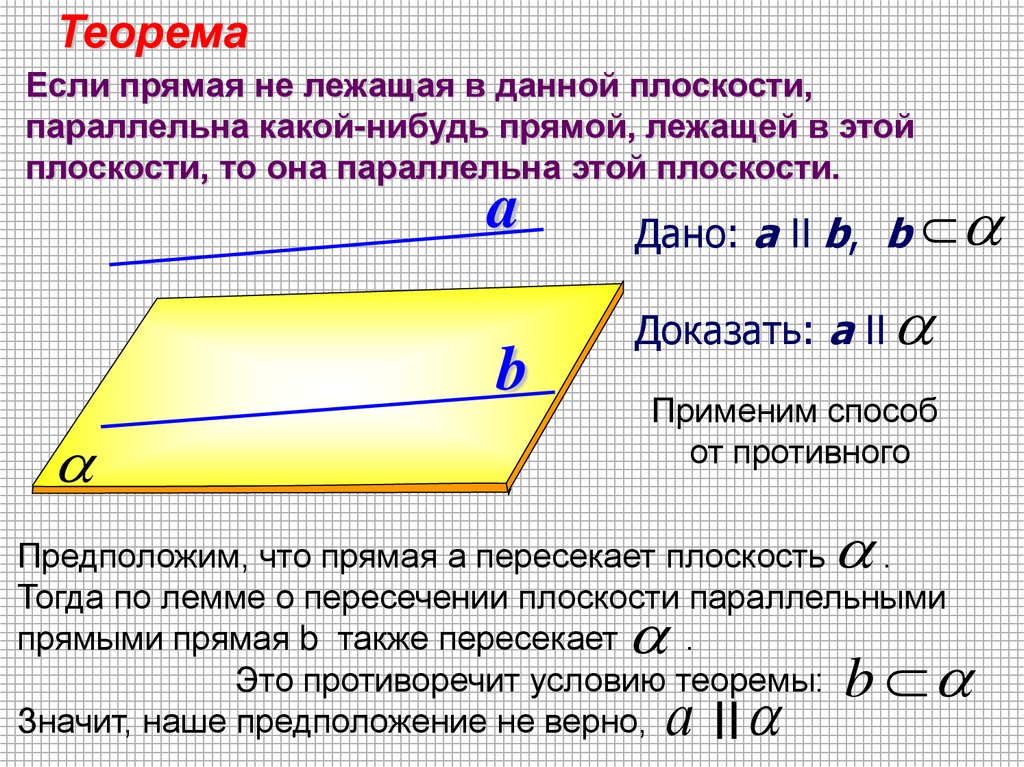
Теорема
Если прямая не лежащая в данной плоскости,
параллельна какой-нибудь прямой, лежащей в этой
плоскости, то она параллельна этой плоскости.
a
b
Дано: a II b, b
Доказать: a II
Применим способ
от противного
Предположим, что прямая а пересекает плоскость
.
Тогда по лемме о пересечении плоскости параллельными
прямыми прямая b также пересекает
.
Это противоречит условию теоремы:
Значит, наше предположение не верно,
II
а
b

9.

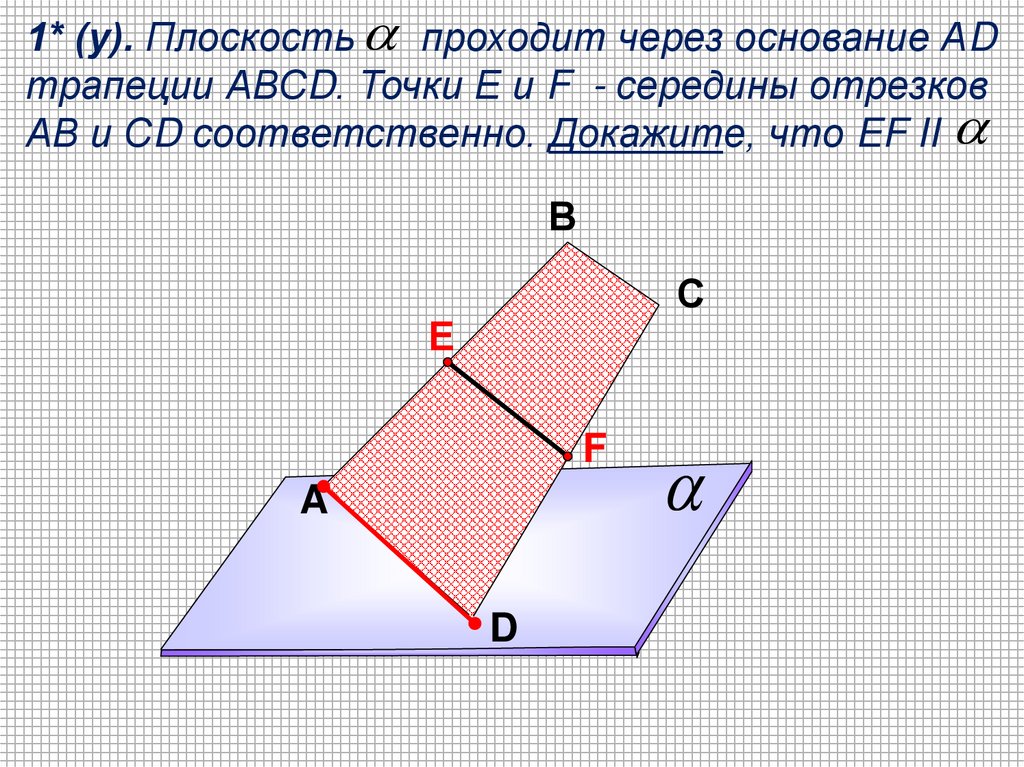
1* (у). Плоскость проходит через основание АD
трапеции АВСD. Точки Е и F - середины отрезков
АВ и СD соответственно. Докажите, что EF II
В
С
Е
F
A
D

10.

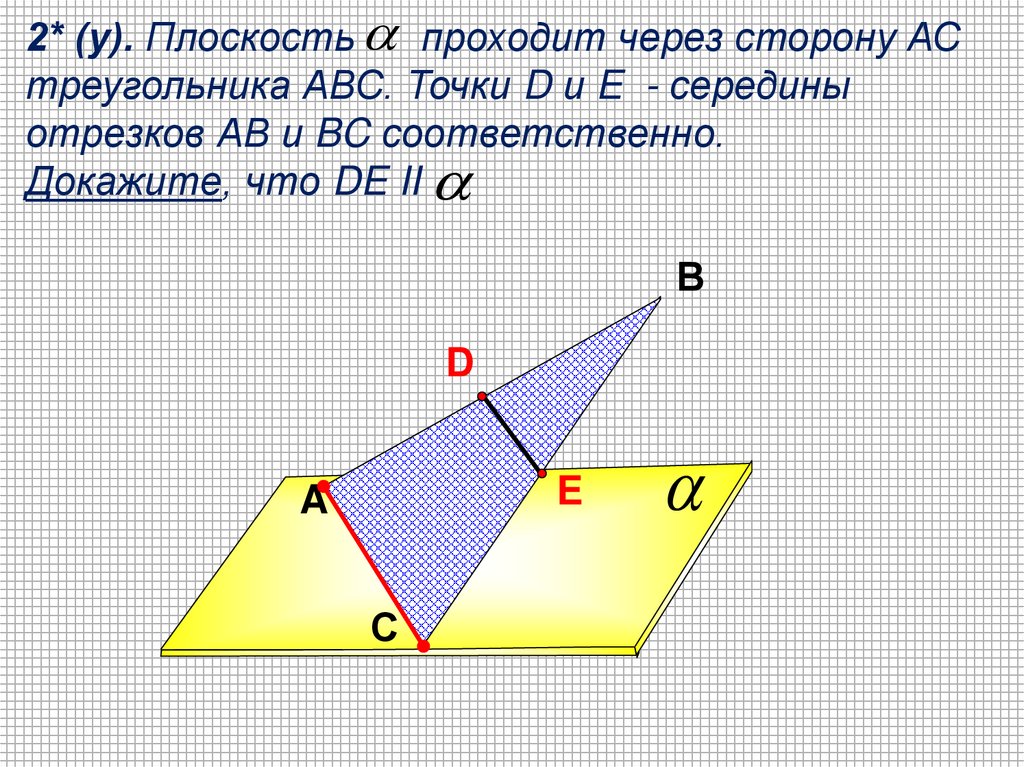
2* (у). Плоскость проходит через сторону АС
треугольника АВС. Точки D и E - середины
отрезков АВ и BC соответственно.
Докажите, что DE II
В
D
E
A
С

11.

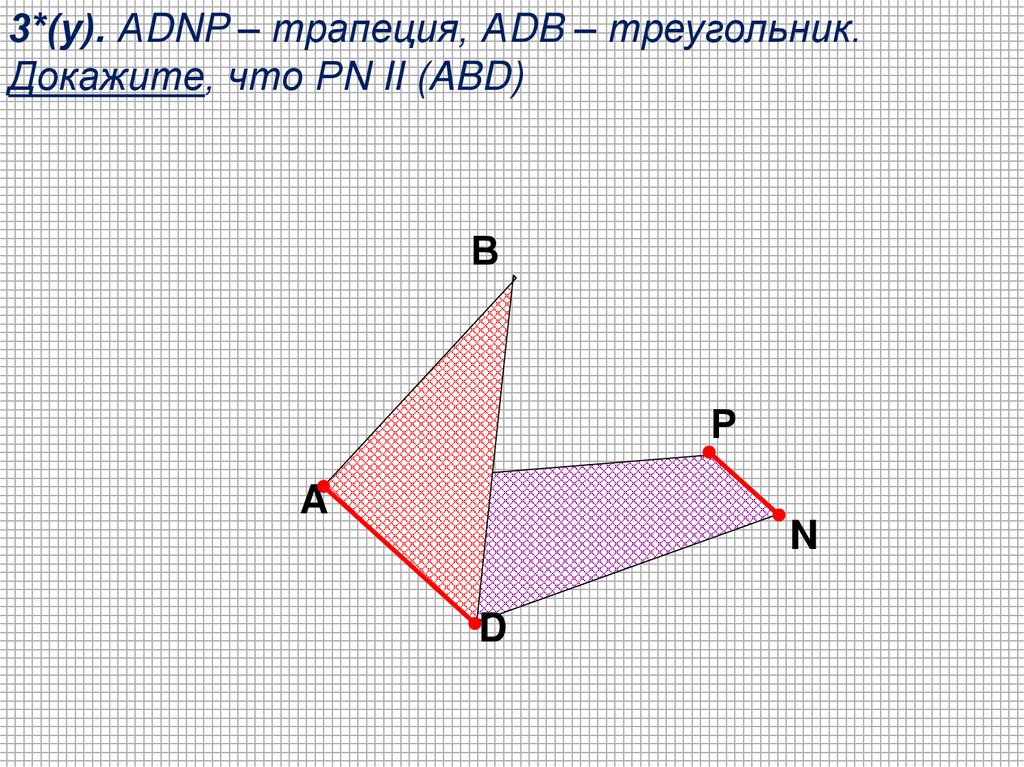
3*(у). АDNP – трапеция, АDB – треугольник.
Докажите, что РN II (ABD)
В
Р
A
N
D

12.

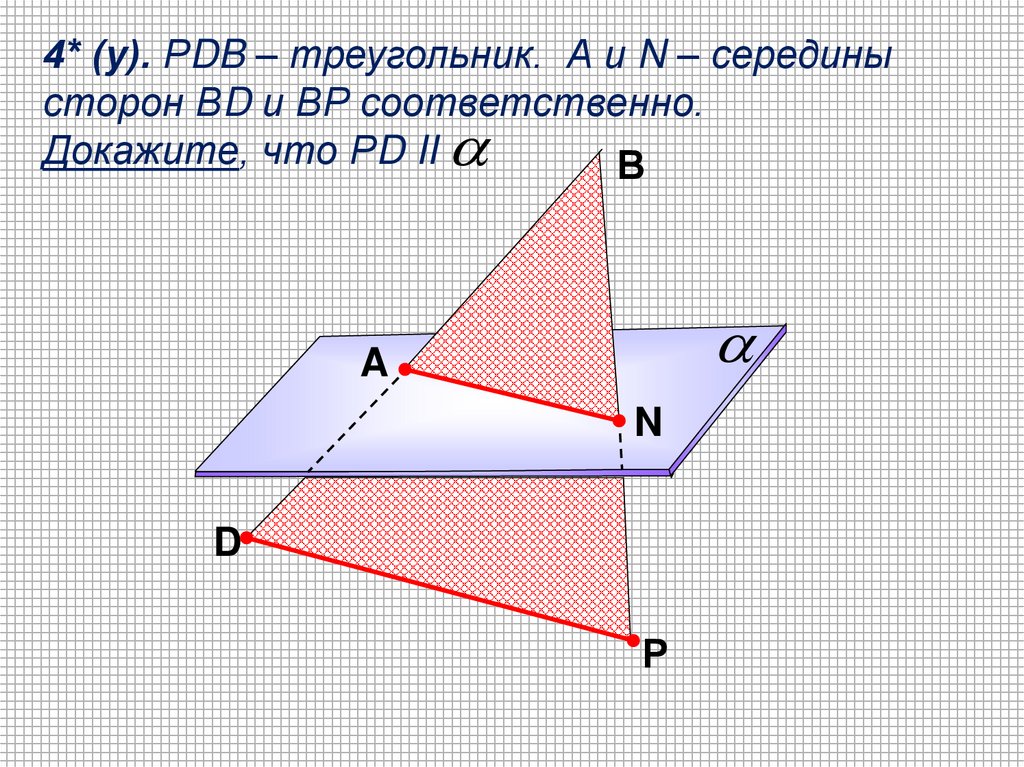
4* (у). РDB – треугольник. А и N – середины
сторон ВD и ВР соответственно.
Докажите, что РD II
В
A
N
D
Р

13.

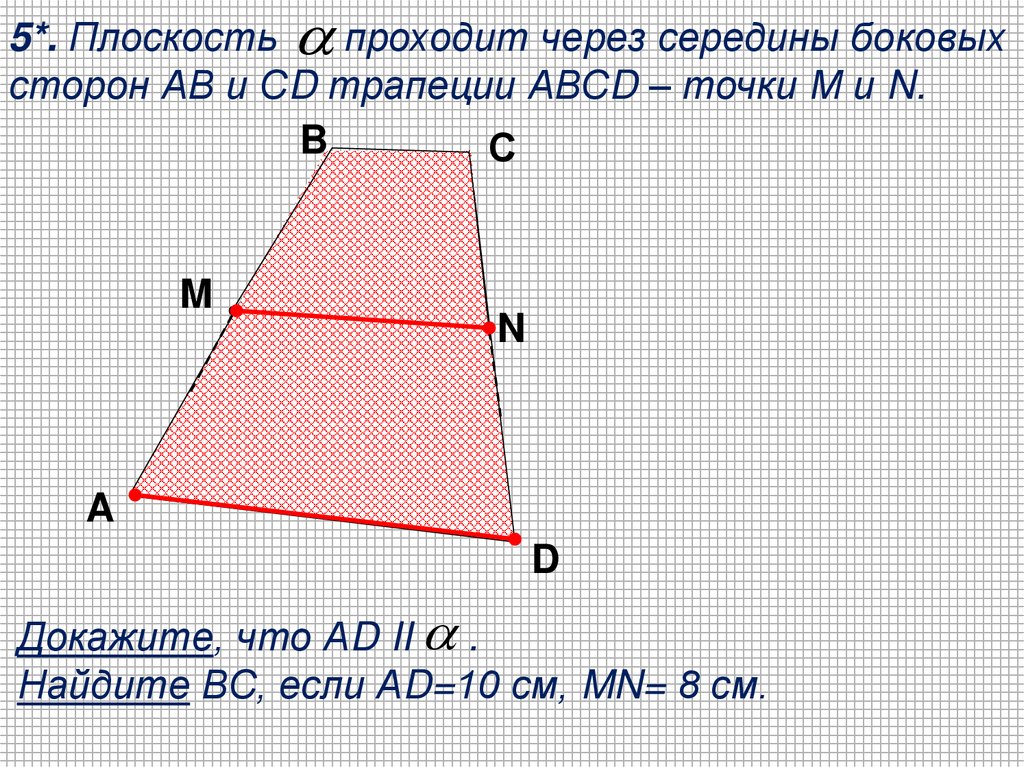
5*. Плоскость проходит через середины боковых
сторон АВ и СD трапеции АВСD – точки М и N.
B
С
M
N
A
D
Докажите, что АD II .
Найдите ВС, если АD=10 см, MN= 8 см.

14.

B
C
С
M
N
A
D
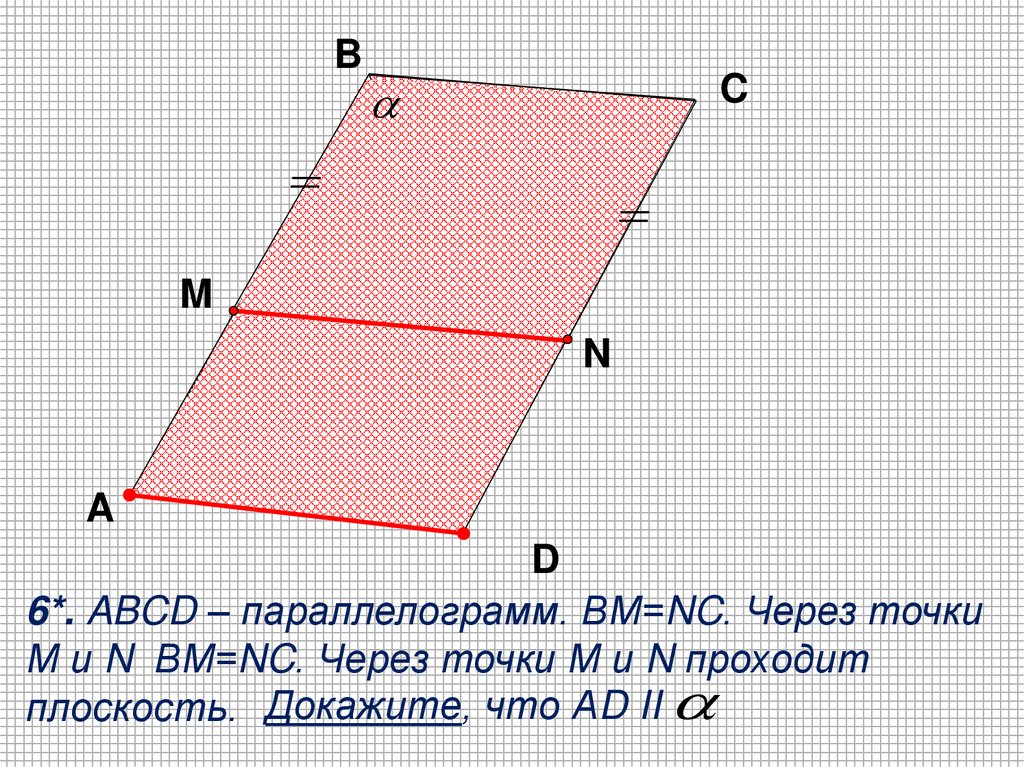
6*. ABCD – параллелограмм. ВМ=NC. Через точки
М и N ВМ=NC. Через точки М и N проходит
плоскость. Докажите, что АD II

15.

На уроке:
1) Новая тема №1* - 6*
Дома:
1) Наизусть теорию п. 4 - 6
2) №18, 22, 23, 26 (на пн)
№27, 32, 33 (на вт)