Определение коэффициентов ряда Фурье

1.

1
Определение коэффициентов ряда Фурье

2.

2
2 m

3.

3
2
1 m
1
A0
f ( t )d t f n ;
m n 1
2 0
2 m
Bk f n sin kn ;
m n 1
m
2
Ck f n cos kn ;
m n 1
k 1, 2, ...
(4)

4.

4
Свойства
периодических несинусоидальных функций,
обладающих симметрией

5.

Симметрия относительно оси абсцисс
f ( t ) f ( t )
A0 B2 C2 B4 C4 ... 0
5

6.

6
Симметрия относительно оси абсцисс
f ( t ) B1 sin t C1 cos t B3 sin 3 t C3 cos3 t
B5 sin 5 t C5 cos5 t ...;
f ( t ) A1m sin t 1 A3m sin 3 t 3
A5m sin 5 t 5

7.

7
Симметрия относительно оси ординат (четная)
f ( t ) f ( t )
0
B1 B2 B3 ... 0

8.

8
Симметрия относительно оси ординат (четная)
f ( t ) A0 C1 cos t C2 cos 2 t C3 cos3 t ...
f ( t ) A0 Ck cos k t
k 1
f ( t ) A0 Akm sin k t .
2
k 1

9.

9
Симметрия относительно начала координат
(нечетная)
f ( t ) f ( t )
A0 C1 C2 C3 ... 0

10.

10
Симметрия относительно начала координат (нечетная)
f ( t ) B1 sin t B2 sin 2 t B3 sin 3 t ...
f ( t ) Bk sin k t .
k 1
f ( t ) Akm sin k t k , где k 0 или 180
k 1

11.

11
Пример аналитического определения
коэффициентов ряда Фурье

12.

12
Периодическое несинусоидальное напряжение
f ( t ) B1 sin t B3 sin 3 t B5 sin 5 t ...

13.

13
Bk
1
2
u ( t )sin k t d t
0
1
1
2
U m sin k t d t U m sin k t d t
0
2U m cos k t
U m sin k t d t
0
k
2
0
2U m
4U m
.
1 1
k
k

14.

14
Функция u(ωt) описывается рядом:
4U m
1
1
u
sin t sin 3 t sin 5 t
3
5
.

15.

15
Пример приближенного определения
коэффициентов ряда Фурье

16.

2
m
m2
2
A0 f n ;
m n 1
m2
4
Bk f n sin kn ;
m n 1
4m2
Ck f n cos kn .
m n 1
16

17.

m
18;
2
2
10 ;
m 18
e18=0
e1 e2 e3
…
e17
17

18.

18
1 18
A0 e n10 ;
18 n 1
1 18
Bk e n10 sin kn10 ;
9 n 1
1 18
Ck e n10 cos kn10 .
9 n 1
В нашем примере A0=0, Bk и Ck – только нечетные.

19.

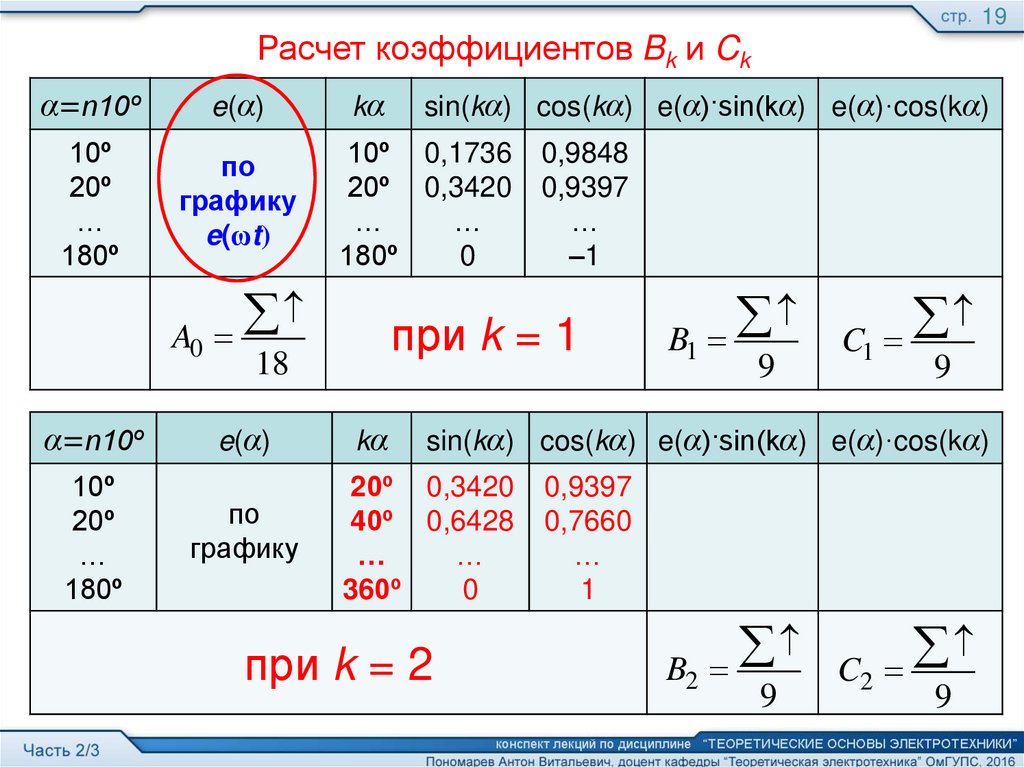
19
Расчет коэффициентов Bk и Ck
α=n10º
e(α)
10º
20º
…
180º
по
графику
e(ωt)
kα
10º 0,1736
20º 0,3420
…
…
180º
0
A
0
α=n10º
10º
20º
…
180º
по
графику
0,9848
0,9397
…
–1
при k = 1
18
e(α)
sin(kα) cos(kα) e(α)·sin(kα) e(α)·cos(kα)
kα
B
1
9
C
1
9
sin(kα) cos(kα) e(α)·sin(kα) e(α)·cos(kα)
20º 0,3420
40º 0,6428
…
…
360º
0
при k = 2
0,9397
0,7660
…
1
B
2
9
C
2
9

20.

20
Akm
Bk2 Ck2 ;
Ck
sin k
k arctg
arctg
.
Bk
cos k
Если Bk<0, то к углу α, полученному на калькуляторе,
необходимо прибавить ±180º!!!

21.

e 151sin t 20 17 sin 3 t 224 52sin 5 t 88 , В.
21
1+3+5
1+3

22.

22
Действующее значение
несинусоидальной функции
T
1
2
F
f
(t )dt .
T0
i I 0 i1 i2 ...
I 0 I1m sin( t 1 ) I 2 m sin(2 t 2 ) ...

23.

23
1
1 2
2
2
2
2
I i dt I 0 I km sin (k t k )
T0
T0
k 1
I pm I qm sin( p t p )sin(q t q ) dt , ( p q ).
p 0
q 0
T
T
T
T
sin (k t k )dt 2 ,
0
2
T
sin( p t p )sin(q t q )dt 0, ( p q),
0

24.

24
I 2 I 02
2
I1m
2
I km 2 I k
2
I 2m
2
2
2
I
I
2
I I 0 1m 2m
2
2
I I 02 I12 I 22 I 32
Аналогично:
E
2
E0
2
E1m
2
E2m
2
2
2
2
2 U1m U 2 m
U U0
2
2
2
2
2
E0 E1 E2
2
2
2
U 0 U1 U 2
,
.