Похожие презентации:
Ряды Фурье для четных и нечетных функций
1.
Разложение в ряд Фурье возможно дляфункций, удовлетворяющих условию теоремы,
сформулированной в предыдущем параграфе.
Для четных и нечетный функций разложение в
ряд Фурье существенно упрощается.
2.
Пусть функция f(x) определена и являетсянечетной на отрезке [-П,П]:
f ( x) f ( x)
Найдем коэффициенты разложения:
an
1
0
1
f ( x) cos nxdx
1
f ( x) cos nxdx f ( x) cos nxdx
0
3.
В первом интеграле делаем замену:x t
dx dt
x2 t2
x1 0 t1 0
1
1
0
f ( x) f (t )
1
f (t ) cos ntdt f ( x) cos nxdx
0
1
f ( x) cos nxdx f ( x) cos nxdx 0
0
0
an 0
4.
Тогдаbn
1
0
1
f ( x) sin nxdx
1
f ( x) sin nxdx f ( x) sin nxdx
0
x t
x1 0 t1 0
dx dt
f ( x) f (t )
x2 t2
5.
10
1
f (t ) sin ntdt f ( x) sin nxdx
0
1
1
f ( x) sin nxdx f ( x) sin nxdx
0
0
2
bn
f ( x) sin nxdx
0
2
f ( x) sin nxdx
0
6.
Таким образом, нечетная на отрезке[-П,П] функция f(x) будет
разлагаться в ряд Фурье
следующим образом:
f ( x) bn sin nx
n 1
7.
Пусть функция f(x) определена и являетсячетной на отрезке [-П,П]:
f ( x) f ( x)
Найдем коэффициенты разложения:
bn
1
0
1
f ( x) sin nxdx
1
f ( x) sin nxdx f ( x) sin nxdx
0
8.
В первом интеграле делаем замену:x t
dx dt
x2 t2
x1 0 t1 0
1
1
0
f ( x) f (t )
1
f (t ) sin ntdt f ( x) sin nxdx
0
1
f ( x) sin nxdx f ( x) sin nxdx 0
0
0
bn 0
9.
Тогдаan
1
0
1
f ( x) cos nxdx
1
f ( x) cos nxdx f ( x) cos nxdx
0
x t
x1 0 t1 0
dx dt
f ( x) f (t )
x2 t2
10.
10
1
f (t ) cos ntdt f ( x) cos nxdx
0
1
1
f ( x) cos nxdx f ( x) cos nxdx
0
0
2
an
f ( x) cos nxdx
0
2
f ( x) cos nxdx
0
11.
Таким образом, четная на отрезке[-П,П] функция f(x) будет
разлагаться в ряд Фурье
следующим образом:
a0
f ( x)
an cos nx
2 n 1
12.
1Разложить в ряд Фурье функцию
f ( x) x
13.
Данная функция удовлетворяет всем условиямтеоремы о разложении функции в ряд Фурье.
Она является нечетной на отрезке [-П,П],
поэтому
an 0
bn
2
2
f ( x) sin nxdx x sin nxdx
0
0
14.
Интеграл берем по частям:u x
du dx
dv sin nxdx
1
v cos nx
n
2 1
1
x cos nx cos nxdx
n
n0
0
2
1
2
n 1
n
1
( 1) sin nx ( 1)
n
n
n
0
0
15.
Тогда ряд Фурье для данной функции будетиметь вид:
n 1
n 1
x bn sin nx 2 ( 1)
n 1,2,3...
n 1
sin nx
n
16.
2Разложить в ряд Фурье функцию
f ( x) x
2
17.
Данная функция удовлетворяет всем условиямтеоремы о разложении функции в ряд Фурье.
Она является четной на отрезке [-П,П], поэтому
bn 0
При n=0:
a0
2
0
2
3
2 x
f ( x)dx x dx
0
3
2
0
2
3
2
18.
При n=1, 2, 3…:an
2
2
f ( x) cos nxdx x
0
2
cos nxdx
0
Интеграл берем по частям:
u x
2
du 2 xdx
dv cos nxdx
1
v sin nx
n
19.
2 1 22
x sin nx x sin nxdx
n
n
0
0
Оставшийся интеграл снова берем по частям:
u x
du dx
dv sin nxdx
1
v cos nx
n
2 1 2
2 1
1
x sin nx x cos nx cos nxdx
n
n
n
n
0
0
0
0
20.
41
n 4
2 x cos nx 0 2 sin nx ( 1) 2
n
n
n
0
0
Тогда ряд Фурье для данной функции будет
иметь вид:
2
a
2
n sin nx
0
x
an cos nx
4 ( 1)
2
2 n 1
3
n
n 1



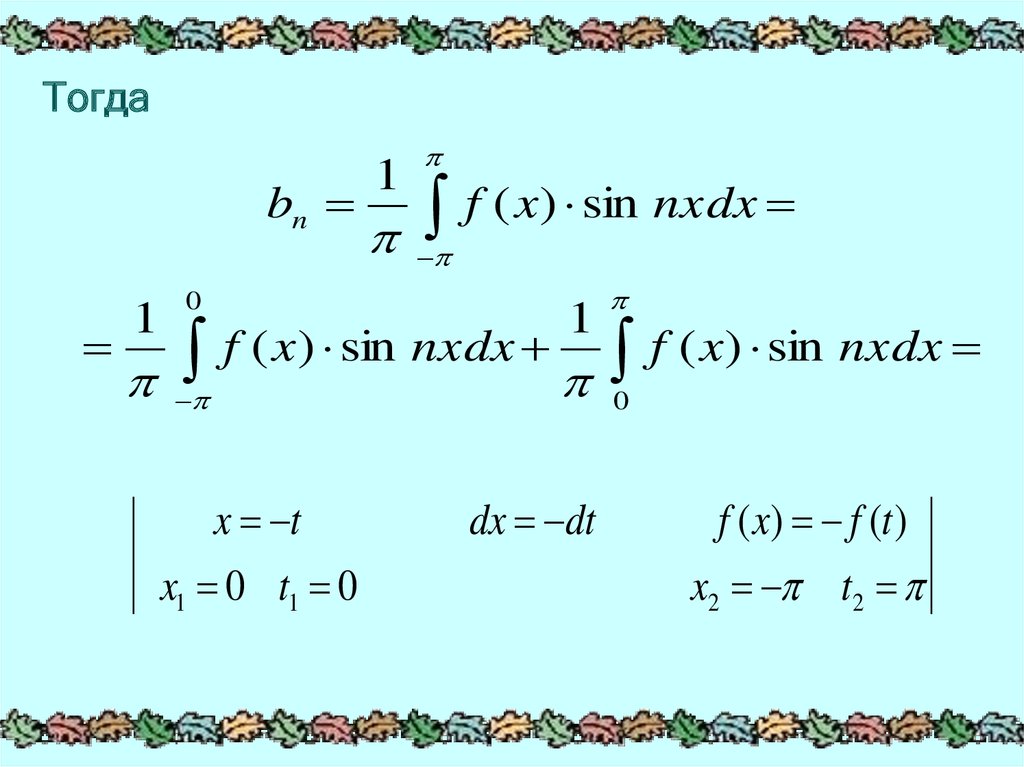
















 Математика
Математика








