Похожие презентации:
Линейные дифференциальные уравнения с постоянными коэффициентами
1.
Лекция 24. Линейные дифференциальныеуравнения с постоянными коэффициентами.
Вид общего решения в зависимости от корней
характеристического уравнения.
1
2.
§ 1. Однородные линейныедифференциальные уравнения с постоянными
коэффициентами (ОЛДУ).
Определение. Дифференциальное уравнение
вида
(1)
y n p1 y n 1 pn 1 y pn y 0 ,
где p1, p2, …, pn R – действительные числа,
называют
однородными
линейными
дифференциальными
уравнениями
с
постоянными коэффициентами.
Чтобы найти общее решение уравнения (1) нужно
построить фундаментальную систему решений,
т.е. систему вида:
2
3.
1) линейно независимую2) L[y1] = 0, L[y2] = 0, …, L[yn] = 0,
тогда общее решение однородного уравнения
(обозначим yoo):
yoo = c1y1 + c2y2 + … + cnyn – общее решение
Построим фундаментальную систему решений
на примере ОЛДУ второго порядка.
y + p1y + p2y = 0.
(2)
Будем искать решение уравнения в виде: y = e x,
тогда: y = e x, y = 2e x.
Подставим y и ее производные в уравнение (2):
2e x + p1 e x + p2e x = 0.
(3)
e x( 2 + p1 + p2) = 0, разделим на e x 0:
3
4.
2 + p1 + p2 = 0(4)
(4)
называется
характеристическим
уравнением для дифференциального уравнения
(2).
Уравнение (4) может имеет два корня. Возможно
три случая:
1) 1 2 – два действительных различных
корня.
2) 1 = 2 – два действительных кратных корня.
3) 1,2 = i – пара комплексно-сопряженных
корней.
i – символ: i2 = -1.
Рассмотрим первый случай.
4
5.
Пусть характеристическое уравнение (4) имееткорни: 1 2 – действительные.
Тогда 1 соответствует e 1x,
2 соответствует e 2x,
следовательно, имеем две функции. Они
являются решениями уравнения (2) и они
линейно независимы. Действительно:
We
1x
,e
2 x
e x
e
1x
e
2 x
2 x
2e
= e 1x 2e 2x - 1e 1xe 2x = e 1xe 2x( 2 - 1) 0.
0
Таким образом, e 1x, e 2x – фундаментальная
система решений, тогда: yoo = c1e 1x + c2e 2x.
1
1
5
6.
Замечание: так как 1 и 2 – произвольные, тоочевидно, что для уравнения второго порядка с
действительными различными корнями e 1x, e 2x –
фундаментальная система решений
Пример. y - 3y + 2y = 0.
Ищем решение в виде: y = e x, тогда:
2 - 3 + 2 = 0 – характеристическое уравнение.
Найдем его корни: 1 = 1, 2 = 2, следовательно,
(ex, e2x) – фундаментальная система решений,
тогда:
yoo = c1ex + c2e2x.
6
7.
Рассмотрим второй случай.Корни действительные и кратные, то есть
характеристическое уравнение (4) имеет корни:
1 = 2 = a – действительный.
Тогда 1 соответствует eax,
2 соответствует eax,
Эта
система
решений
не
является
фундаментальной, т.к.:
ax
W e ,e
ax
aeax
e
ax
e
ax
0
ax
ae
[eax, eax] - линейно зависима.
7
8.
Попробуем для второго корня найти функцию,которая: 1) удовлетворяла бы уравнению 2 и
при этом система функций была бы
фундаментальной.
Будем искать решение в виде:
y = u(x)eax
Найдем производные:
y = u eax + uaeax,
y = u eax + u aeax + u aeax + ua2eax =
= u eax + 2u aeax + ua2eax.
Подставим их в уравнение 2: y + p1y + p2y = 0:
u eax + 2u aeax + ua2eax + p1u eax + p1uaeax +
+ p2ueax = 0.
Сократим на eax и сгруппируем:
8
9.
u + u (2a + p1) + u(a2 + p1a + p2) = 0.Так как a – корень характеристического
уравнения, то выражение, подчеркнутое двумя
линиями: a2 + p1a + p2 = 0.
В силу теоремы Виета: 1 + 2 = - p1, тогда:
2a = -p1 2a + p1 = 0.
Следовательно: u = 0. Решаем его
последовательным интегрированием:
u = с1 u = c1dx + c2 = c1x + c2.
Пусть с1 = 1, с2 = 0 u = x, имеем:
1 соответствует eax,
2 соответствует xeax,
9
10.
axW e , xe
ax
aeax
e ax
xeax
e
e ax xae ax
ax
0
Построенная таким образом система функций
является фундаментальной системой решений,
тогда общее решение однородного уравнения
имеет вид:
yoo = c1eax + c2xeax = eax(c1 + c2x).
Если
встречаются
кратные
корни,
то
фундаментальная система строится таким
образом: первому корню ставится eax, а
каждому последующему корню – предыдущая
функция, умноженная на x.
10
11.
Пример.y - 2y + y = 0.
Решение ищем в виде:
y = e x.
Характеристическое уравнение имеет вид:
2 – 2 + 1 = 0,
( - 1)2 = 0,
1 = 1, 2 =1,
1 = 1 соответствует ex,
2 = 1 соответствует xex,
Тогда:
yoo = c1ex + c2xex = ex(c1 + c2x).
11
12.
Третий случай.Корни мнимые: 1,2 = i.
Лемма 1. Если y = u(x) + v(x)i – решение
уравнения L[y] = 0, то:
u(x) – решение L[u] = 0,
v(x) – решение L[v] = 0,
Доказательство.
L[y] = L[u + iv] = L[u] + L[iv] = L[u] + iL[v] – в
силу линейности оператора.
Так как L[y] = 0 L[u] + iL[v] = 0 L[u] = 0,
L[v] = 0.
Ч.т.д.
12
13.
Формулы Эйлера.Они
связывают
функции
комплексного
аргумента ez, cosz, sinz, где z = a + bi или
z = a - bi. Они имеют вид:
ei = cos + isin
e-i = cos - isin
где: - действительное число.
Частные решения в случае комплексных
корней.
1 = + i соответствует e( + i)x,
2 = - i соответствует e( - i)x,
По формулам Эйлера имеем:
e( + i)x = e xe xi = e x(cos x + isin x)
e( - i)x = e xe- xi = e x(cos x - isin x)
13
14.
1 соответствует e xcos x + ie xsin x,2 соответствует e xcos x - ie xsin x,
То есть: e xcos x + ie xsin x - решение.
Тогда в силу леммы:
e xcos x и e xsin x - также решения. Имеем две
функции.
W[e xcos x, e xsin x] 0,
Значит систему двух функций можно считать
фундаментальной.
1 = + i соответствует e xcos x,
2 = - i соответствует e xsin x,
Тогда: yoo = c1e xcos x + c2e xsin x =
= e x(c1cos x + c2sin x).
14
15.
Пример.y + y = 0
Характеристическое уравнение:
2 + 1 = 0 2 = -1 1,2 = 1 = 1i = i.
Следовательно:
0
1
1 = + i соответствует cosx,
2 = - i соответствует sinx,
Тогда:
yoo = c1cosx + c2sinx.
15
16.
§ 2. Построение решений ОЛДУ в общемслучае.
Корни характеристиВид слагаемого в
ческого уравнения
общем решении
ce x
- действительный корень
- действительный корень (c0 + c1x + c2x2 + … +
кратности k
+ ck-1xk-1)e x
i – пара комплексно- e x(Ccos x + Dsin x)
сопряженных корней
i – пара комплексно- e x [(C0 + C1x + … +
сопряженных корней
+ Ck-1xk-1)cos x +
кратности k
+ (D0 + D1x + … +
+ Dk-1xk-1)sin x]
16
17.
§ 3. Неоднородные линейныедифференциальные уравнения с
переменными коэффициентами.
Рассмотрим уравнение вида:
y(n) + a1(x)y(n-1) + … + an(x)y = f (x)
(5)
или
L[y] = f (x).
(6)
Для дифференциального уравнения (5) ставится
Задача Коши:
y(x0) = y0, y (x0) = y1, …, y(n-1)(x0) = yn-1.
При рассмотрении уравнений (5) используют:
Теорема 1. Если ~
y x - есть решение уравнения
L[y] = f (x), а y0(x) - есть решение уравнения
y x + y0(x) - есть решение L[y] = f (x)
L[y] = 0, то ~
17
18.
Доказательство.Применим линейный оператор:
L[ ~
y x + y0(x)] = L[ ~
y x ] + L[y0(x)] = f (x).
f (x)
0
Ч.т.д.
Замечание. Из теоремы 1 следует, что сумма
любого решения неоднородного уравнения и
любого решения однородного уравнения, есть
решение неоднородного уравнения.
18
19.
Теорема 2. Если y1(x) – решение L[y] = f1(x), афункция y2(x) – решение L[y] = f2(x), то y1 + y2 –
есть решение уравнения L[y] = f1(x) + f2(x).
Доказательство.
Применим линейный оператор L к сумме y1 + y2:
L[y1+y2]=L[y1] + L[y2] = по условию = f1(x)+ f2(x).
Ч.т.д.
Замечание. Из теоремы видно, что решение
уравнения L[y] = f1(x) + f2(x) можно найти,
решая уравнения L[y1] = f1(x), L[y2] = f2(x),
путем сложения y = y1 + y2.
19
20.
Теорема 3. Если u(x) + v(x)i – есть решениеуравнения L[y] = u(x) + v(x)i, где u(x) и v(x) –
действительные функции, то u(x) и v(x) есть
решение уравнений L[y] = U, L[y] = V
соответственно.
Без доказательства.
Теорема 4. (О структуре общего решения
линейного неоднородного дифференциального
уравнения). Общее решение уравнения
L[y] y(n) + a1(x)y(n-1) + … + an(x)y = f (x), где:
1) a < x < b,
2) a1(x), a2(x), …, an(x), f (x) – непрерывные
функции,
20
21.
4) y(k) < + , k = 0, 1, 2, …, n-1,выражаются формулой:
yон = учн + уоо,
где: yон – общее решение неоднородного
уравнения L[y] = f (x),
yчн – частное решение неоднородного
уравнения L[y] = f (x),
yоо – общее решение однородного уравнения
L[y] = 0.
Без доказательства.
21
22.
§ 4. Неоднородные линейныедифференциальные уравнения с постоянными
коэффициентами (НЛДУ).
Схема построения решения. Метод подбора.
L[y] y(n) + a1(x)y(n-1) + … + an(x)y = f (x) – НЛДУ.
Схема построения общего решения.
1) Рассмотрим однородное уравнение: L[y] = 0.
2) Для однородного уравнения составляем
характеристический многочлен Pn( ) = 0 и
находим корни: 1, 2, …, n.
3) Записываем фундаментальную систему
решений, т.е. систему 1, 2, …, n.
4) Строим общее решение однородного уравнения
22
23.
nyoo ck k
k 1
5) Находим какое-либо одно решение ~
y x , такое
y f x
что: L ~
y x
yчн = ~
6) В соответствии с теоремой 4:
n
~
c
yон = учн + уоо =
k k y x0
k 1
23
24.
Применение метода подбора.I. Рассмотрим: L[y] = Pm(x) – правая часть
многочлен.
Характеристическое уравнение: Pn( ) = 0,
находим корни: 1, 2, …, n и записываем уоо.
При отыскании yчн необходимо обращать
внимание на корни характеристического
уравнения. Возможны два случая:
а) среди корней характеристического уравнения
нет нулевых, тогда: yчн = Qm(x) с неизвестными
коэффициентами.
Коэффициенты
этого
многочлена
определяются
по
методу
неопределенных
коэффициентов,
после
24
25.
подстановки в исходное уравнение иприравнивания коэффициентов при одинаковых
степенях х.
б)
Среди
корней
характеристического
уравнения есть нулевые корни кратности r.
1 = 2 = … = n = 0, тогда yчн = xrQm(x), где:
Qm(x) = A0xm + A1xm-1 + … + Am-1x + Am.
Нахождение коэффициентов производится
методом неопределенных коэффициентов:
L[xrQ(x)] = Pm(x).
II. Рассмотрим: L[y] = e xPm(x), R.
Самостоятельно.
25
26.
Обобщение метода подбораПравая часть
Связь с корнями
Вид частного решения
Тип дифференциальног характеристического
неоднородного
о уравнения
уравнения
уравнения учн
I
Pm(x) - многочлен
а) 0 не является корнем
Qm(x) – многочлен c
характеристического
неопределенными
уравнения
коэффициентами
б) 0 является корнем
xrQm(x)
характеристического
уравнения кратности r
x
II
e Pm(x)
а) не является корнем
Qm(x)e x
– действительное характеристического
уравнения
число
б) является корнем
xrQm(x)e x
характеристического
уравнения кратности r
III
e x(Pm(x)cos x +
а) i не является
e x(Qp(x)cos x +
корнем
+ Ps(x)sin x)
+ Qp(x)sin x),
характеристического
где: p = max{m,s}
m s
уравнения
б) i является
xre x(Qp(x)cos x +
корнем
+ Qp(x)sin x),
характеристического
где: p = max{m,s}
уравнения кратности r
26
27.
Еслив
линейном
дифференциальном
уравнении имеются переменные коэффициенты
или правая часть не имеет специального вида,
то применяют другие методы.
§ 5. Метод вариации произвольных
постоянных (n = 2)
Пусть y + p(x)y + q(x)y = f (x),
(7)
где f(x) не является правой частью
специального
вида,
p(x)
и
q(x)
–
дифференцируемы на [a,b].
Рассмотрим кроме (7) уравнение:
y + p(x)y + q(x)y = 0,
(8)
которое является однородным.
27
28.
Если y1(x) и y2(x) – фундаментальная системарешений уравнения, то:
уоо = с1y1(x) + с2y2(x).
Чтобы найти общее решение (7) Лагранж
предложил метод вариации: искать
уон = с1(x)y1(x) + с2(x)y2(x),
где: с1(x) и с2(x) – переменные, и накладывать
на них ограничения. Найдем производную:
y'он c1 ' y1 c1 y1 ' c2 ' y2 c2 y2 '
Накладываем ограничения и требуем, чтобы
с1 ' y c2 ' y2 0
тогда
y'он c1 y1 ' c2 y2 '
28
29.
Находим теперь вторую производную:y' 'он c1 ' y1 ' c1 y1 ' ' c2 ' y'2 c2 y2 ' '
Подставим y он , y'он и y ' 'он в уравнение (7), имеем
c1 y1 ' c1 y1 ' ' c'2 y2 ' c 2 y ' ' p(c1 y1 ' c2 y2 ' )
q(c1 y1 c2 y2 ) f ( x)
Группируя, получаем:
c1 ' y1 ' c'2 y2 '
c1( y1 ' ' py1 ' qy1 ) c2 ( y2 ' ' py2 ' qy2 ) f ( x)
=0
В итоге:
c1 ' y1 ' c2 ' y2 ' f ( x)
=0
29
30.
Составим систему уравнений из ограничения иполученного последнего уравнения.
c1 ' y1 c2 ' y 2 0
c1 ' y1 ' c2 ' y 2 ' f ( x)
Полученная система линейна относительно
неизвестных c1 ' и c2 '.
Определитель Вронского для этой системы:
W [ y1, y2 ]
y1 y2
y1 ' y2 '
0
Решаем данную систему по методу Крамера:
30
31.
0y1
y2
y2
0
y1 ' f ( x)
f ( x)
2 ( x);
ñ1 '
1 ( x); ñ2 '
y1 y2
y1 y2
y1 ' y2 '
y1 y2
Отсюда, решая дифференциальные уравнения,
получаем: ñ ( x)dx c*
1
1
*
ñ2 2 ( x)dx c2
1
Таким образом, окончательное решение имеет
вид:
yîí
*
1 ( x)dx c1
y
1
*
2 ( x)dx c2
y
2
31
32.
Пример. y ' ' y tgxЗапишем однородное уравнение:
y' ' y 0
Это ЛОДУ 2-го порядка с постоянными
коэффициентами, т.к. из (7) p(x) = 0, q(x) = 1
Составляем соответствующее ему
характеристическое уравнение:
1 0 12 i 0 1 i
2
x
Примечание: e e 1
Тогда, общее решение однородного уравнения:
0x
yîî c1 cos x c2 sin x
32
33.
Используем метод вариации произвольныхпостоянных,
ищем
общее
решение
неоднородного уравнения в виде:
yон с1 ( x) cos x c2 ( x) sin x
Составляем систему уравнений и решаем её:
sin x
c1 ' cos x c2 ' sin x 0
c1 ' sin x c2 ' cos x tgx cos x
c1 ' cos x sin x c2 ' sin 2 x c1 ' sin x cos x c2 ' cos 2 x tgx cos x
c2 ' tgx cos x c2 ' sin x
c 2 sin dx c cos x c
*
2
*
2
33
34.
sin xc1 '
cos x
2
2
2
sin x
sin x(cos xdx) *
*
c1
dx c1
c1
2
cos x
cos x
sin 2 xd (sin x) *
c1
2
(1 sin x)
t dt
(t 1) 1
*
*
[sin x t ] 2
c1
dt
c
1
2
t 1
(t 1)
1
*
dt 2 dt c1
t 1
2
2
34
35.
1 t 11 sin x 1
*
*
t ln
c1 sin x ln
c1
2 t 1
2 sin x 1
1 sin x 1
*
yîí sin x ln
c1 cos x
2 sin x 1
cos x
yîí
*
c1 cos x
*
c2 sin
*
c2
sin x
1
sin x 1
x cos x ln
2
sin x 1
35

































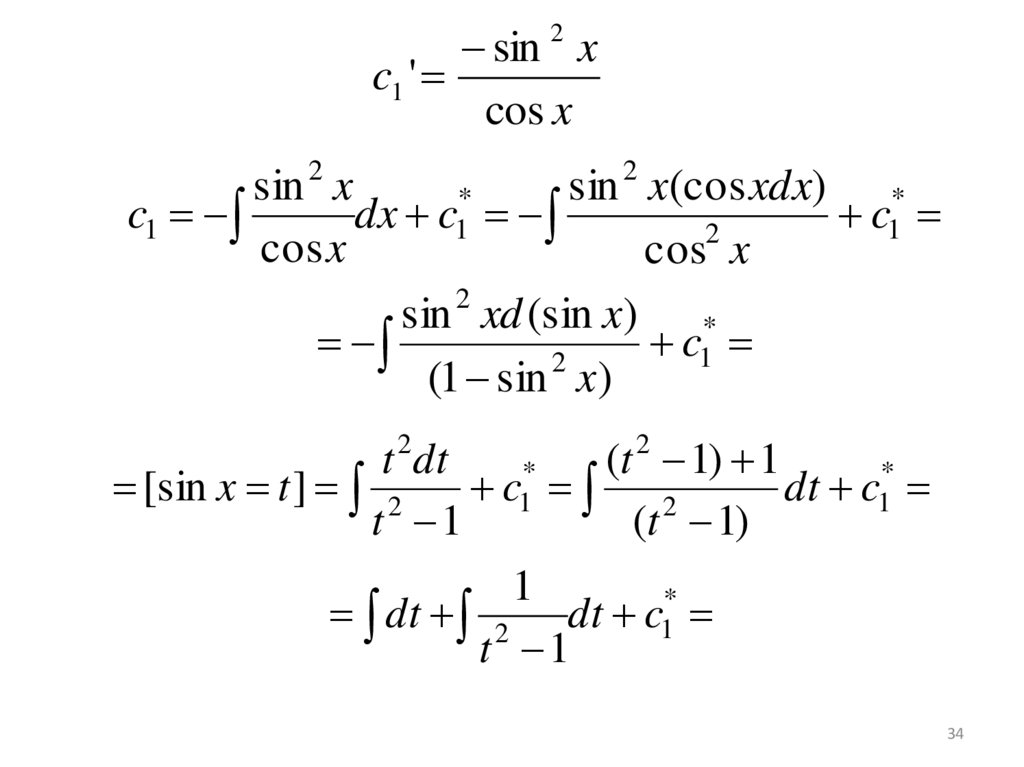
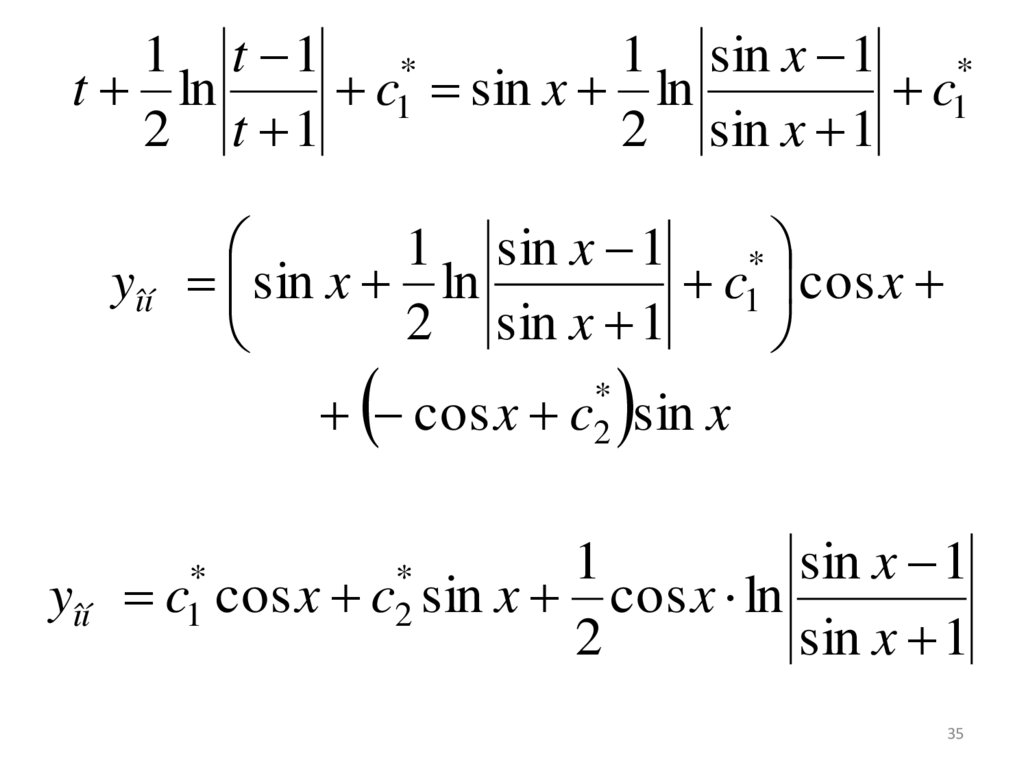
 Математика
Математика








