Похожие презентации:
Тригонометрическая система функций. Ряды Фурье. Разложение функций в ряд Фурье
1.
Лектор Буганова С.Н.Тригонометрическая система
функций. Ряды Фурье.
Разложение функций в ряд
Фурье. Формулировка условий
разложимости в случае
равномерной сходимости
Дисциплина Математика 2
Лекция 10
2. План лекции
1. Ряды Фурье: основные понятия.2. Ряды Фурье для четных и нечетных
функций.
3. Примеры.
3.
Для тригонометрического ряда, каки для степенного ряда, можно
установить условия разложения
функций.
Если функция y=f(x) интегрируема
на отрезке [-П,П] и
разлагается в
a0
тригонометрический
ряд
f ( x)
2
(an cosnx bn sin nx)
n 1
который можно интегрировать
почленно при умножении его
на ограниченную функцию, то
это разложение единственно.
1
4.
Для определениякоэффициентов
разложения будем
использовать
ортогональность
системы
тригонометрических
функций.
Проинтегрируем (1) на
отрезке [-П,П].
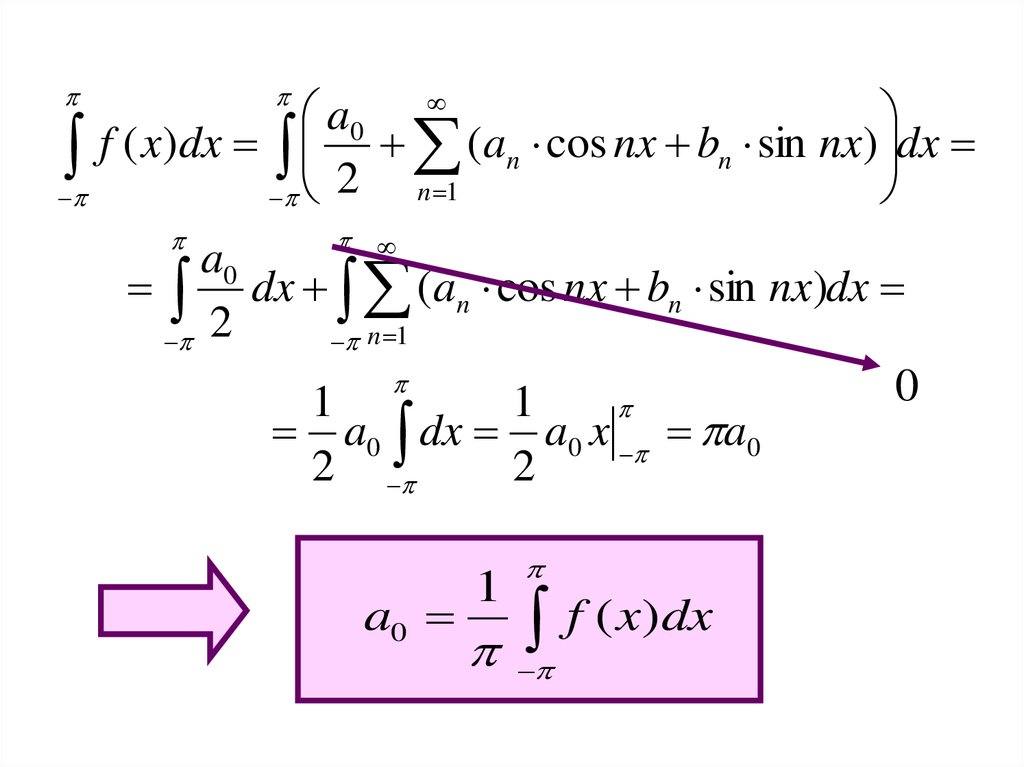
5.
a0(an cos nx bn sin nx) dx
f ( x)dx 2
n 1
a0
dx (an cos nx bn sin nx)dx
2
n 1
0
1
1
a0 dx a0 x a0
2
2
a0
1
f ( x)dx
6.
Для определениякоэффициентов an и bn
последовательно
умножим обе части (1) на
сначала на cos(nx), а потом
на sin(nx) и проинтегрируем
на отрезке [-П,П].
Все интегралы в правой
части, кроме содержащих
квадраты этих функций,
равны нулю.
Полученные формулы
будут определять
единственным образом
7.
f ( x) cos nxdx a cosn
2
nxdx an
an
1
f ( x) cos nxdx
f ( x) sin nxdx bn sin 2 nxdx bn
bn
1
f ( x) sin nxdx
8.
я функции f(x), интегрируемой на отрез[-П,П] числа a0, an, bn называются
коэффициентами ряда Фурье, а ряд (1) с
этими коэффициентами называется
рядом Фурье функции f(x).
9.
Для определения сходимостиряда Фурье вводится понятие
периодического продолжения
функции, заданной на отрезке
[-Т,Т].
кция F(x), определенная на всей число
и периодическая с периодом Т, являе
риодическим продолжением функции
если F(x)=f(x) на отрезке [-П,П].
10.
ряд Фурье сходится к функциезке [-П,П], то он сходится на
овой прямой к ее периодиче
продолжению.
11.
Пусть функция y=f(x)непрерывна вместе со
своей производной на
отрезке [-П,П], или они
имеют на этом отрезке
конечное число точек
разрыва.
Тогда
12.
1яд Фурье функции f(x) сходится на все
числовой прямой, и в каждой точке
непрерывности f(x) в интервале (-П,П]
сумма ряда равна значению f(x)
в этой точке.
13.
2В каждой точке разрыва функции х /
сумма ряда равна полусумме
носторонних пределов f(x) в этой точк
1
lim f ( x) lim f ( x)
x x 0
2 x x 0
14.
3На концах отрезка [-П,П]
сумма ряда равна
1
f ( ) f ( )
2
15.
4Для любой точки х, не принадлежащей
отрезку [-П,П] утверждения 1-3
справедливы для периодического
продолжения F(x) функции f(x).
16.
Для четных и нечетный функций разложение вряд Фурье существенно упрощается.
17.
Пусть функция f(x) определена и являетсянечетной на отрезке [-П,П]:
f ( x) f ( x)
Найдем коэффициенты разложения:
an
1
0
1
f ( x) cos nxdx
1
f ( x) cos nxdx f ( x) cos nxdx
0
18.
В первом интеграле делаем замену:x t
dx dt
x2 t2
x1 0 t1 0
1
1
0
f ( x) f (t )
1
f (t ) cos ntdt f ( x) cos nxdx
0
1
f ( x) cos nxdx f ( x) cos nxdx 0
0
0
an 0
19.
Тогдаbn
1
0
1
f ( x) sin nxdx
1
f ( x) sin nxdx f ( x) sin nxdx
0
x t
x1 0 t1 0
dx dt
f ( x) f (t )
x2 t2
20.
10
1
f (t ) sin ntdt f ( x) sin nxdx
0
1
1
f ( x) sin nxdx f ( x) sin nxdx
0
0
2
bn
f ( x) sin nxdx
0
2
f ( x) sin nxdx
0
21.
Таким образом, нечетная на отрезке[-П,П] функция f(x) будет
разлагаться в ряд Фурье
следующим образом:
f ( x) bn sin nx
n 1
22.
Пусть функция f(x) определена и являетсячетной на отрезке [-П,П]:
f ( x) f ( x)
Найдем коэффициенты разложения:
bn
1
0
1
f ( x) sin nxdx
1
f ( x) sin nxdx f ( x) sin nxdx
0
23.
В первом интеграле делаем замену:x t
dx dt
x2 t2
x1 0 t1 0
1
1
0
f ( x) f (t )
1
f (t ) sin ntdt f ( x) sin nxdx
0
1
f ( x) sin nxdx f ( x) sin nxdx 0
0
0
bn 0
24.
Тогдаan
1
0
1
f ( x) cos nxdx
1
f ( x) cos nxdx f ( x) cos nxdx
0
x t
x1 0 t1 0
dx dt
f ( x) f (t )
x2 t2
25.
10
1
f (t ) cos ntdt f ( x) cos nxdx
0
1
1
f ( x) cos nxdx f ( x) cos nxdx
0
0
2
an
f ( x) cos nxdx
0
2
f ( x) cos nxdx
0
26.
Таким образом, четная на отрезке[-П,П] функция f(x) будет
разлагаться в ряд Фурье
следующим образом:
a0
f ( x)
an cos nx
2 n 1
27.
1Разложить в ряд Фурье функцию
f ( x) x
28.
Данная функция удовлетворяет всем условиямтеоремы о разложении функции в ряд Фурье.
Она является нечетной на отрезке [-П,П],
поэтому
an 0
bn
2
2
f ( x) sin nxdx x sin nxdx
0
0
29.
Интеграл берем по частям:u x
du dx
dv sin nxdx
1
v cos nx
n
2 1
1
x cos nx cos nxdx
n
n0
0
2
1
2
n 1
n
1
( 1) sin nx ( 1)
n
n
n
0
0
30.
Тогда ряд Фурье для данной функции будетиметь вид:
n 1
n 1
x bn sin nx 2 ( 1)
n 1,2,3...
n 1
sin nx
n
31.
2Разложить в ряд Фурье функцию
f ( x) x
2
32.
Данная функция удовлетворяет всем условиямтеоремы о разложении функции в ряд Фурье.
Она является четной на отрезке [-П,П], поэтому
bn 0
При n=0:
a0
2
0
2
3
2 x
f ( x)dx x dx
0
3
2
0
2
3
2
33.
При n=1, 2, 3…:an
2
2
f ( x) cos nxdx x
0
2
cos nxdx
0
Интеграл берем по частям:
u x
2
du 2 xdx
dv cos nxdx
1
v sin nx
n
34.
2 1 22
x sin nx x sin nxdx
n
n
0
0
Оставшийся интеграл снова берем по частям:
u x
du dx
dv sin nxdx
1
v cos nx
n
2 1 2
2 1
1
x sin nx x cos nx cos nxdx
n
n
n
n
0
0
0
0
35.
41
n 4
2 x cos nx 0 2 sin nx ( 1) 2
n
n
n
0
0
Тогда ряд Фурье для данной функции будет
иметь вид:
2
a
2
n sin nx
0
x
an cos nx
4 ( 1)
2
2 n 1
3
n
n 1
36.
Задания на СРСПреобразование Фурье Разложите в ряд
элементарные функции [ 1,3].
Решение задач по теме [ 2. ИДЗ – 12.3 ].
Задания на СРСП
1. Интегралы (преобразования) Фурье
[1, 3].
37.
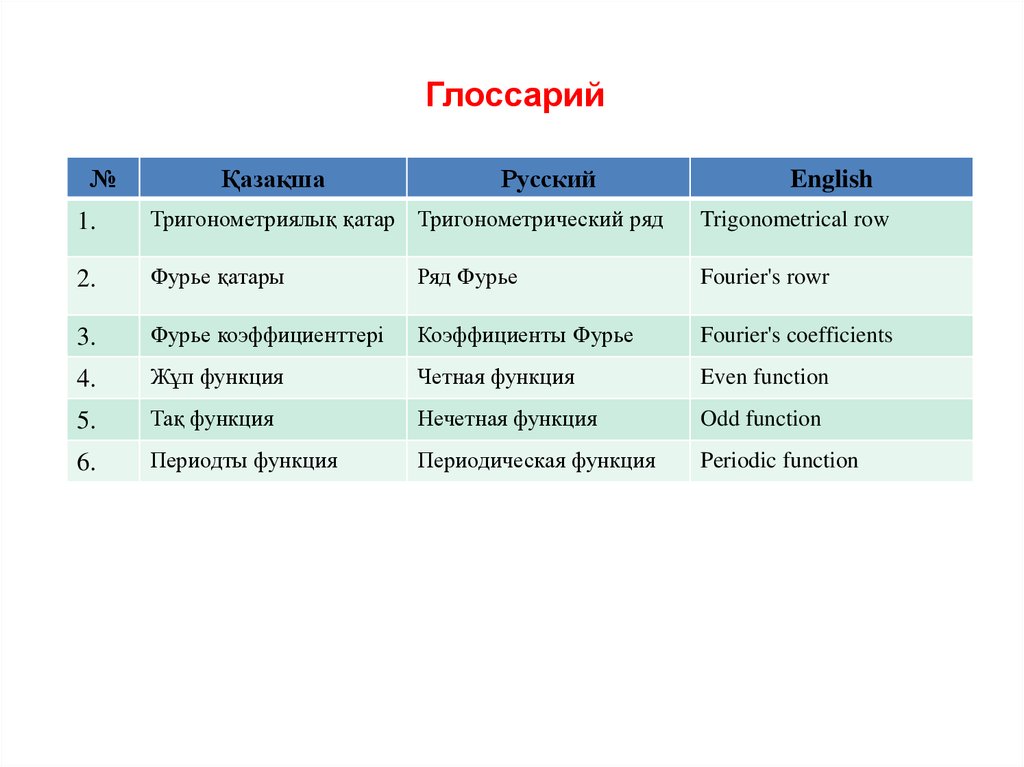
Глоссарий№
Қазақша
Русский
English
1.
Тригонометриялық қатар Тригонометрический ряд
Trigonometrical row
2.
Фурье қатары
Ряд Фурье
Fourier's rowr
3.
Фурье коэффициенттері
Коэффициенты Фурье
Fourier's coefficients
4.
Жұп функция
Четная функция
Even function
5.
Тақ функция
Нечетная функция
Odd function
6.
Периодты функция
Периодическая функция
Periodic function
38.
ЛитератураОсновная:
1.Пискунов Н.С. Дифференциальное и интегральное
исчисления. М. 2006.
2. Сборник индивидуальных заданий по высшей
математике:
Учеб. пособие в 4 частях / Под общей редакцией А.П.
Рябушко. - Мн.: Выш. шк., 2011, часть 3.
Дополнительная:
3. Власова Е.А. Ряды: учебник для вузов /Под ред.
Зарубина В.С., Крищенко А.П.. – 3-е изд. –М.:МГТУ им.
Н.Э.Баумана, 2006. – 616 с.


















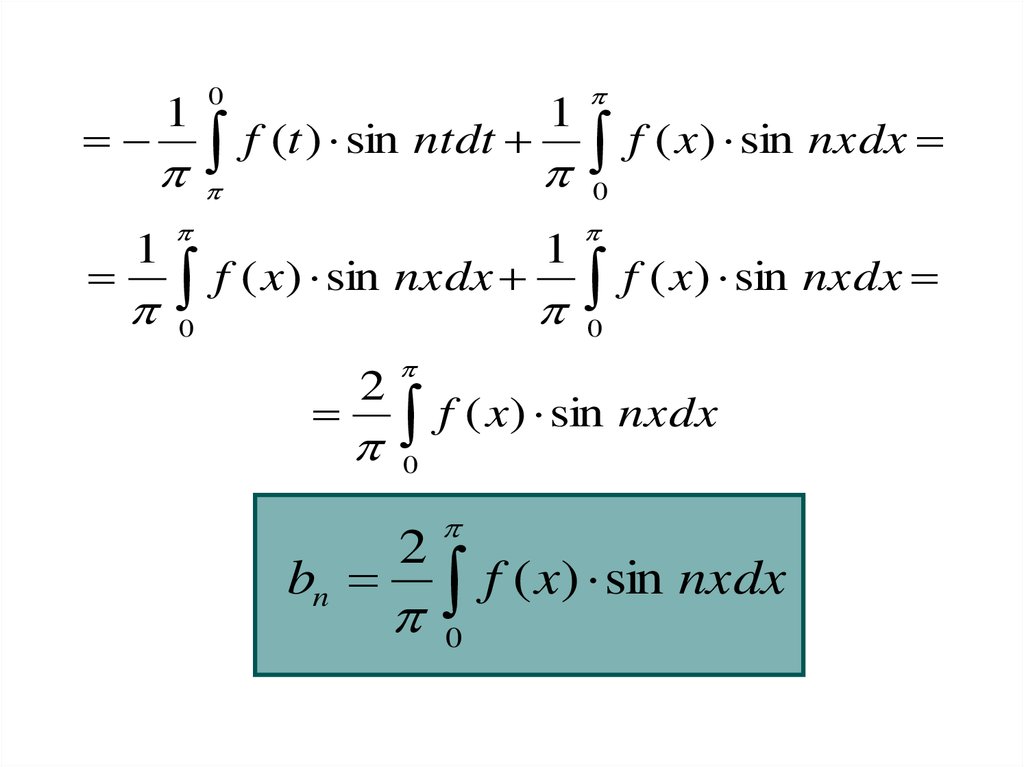



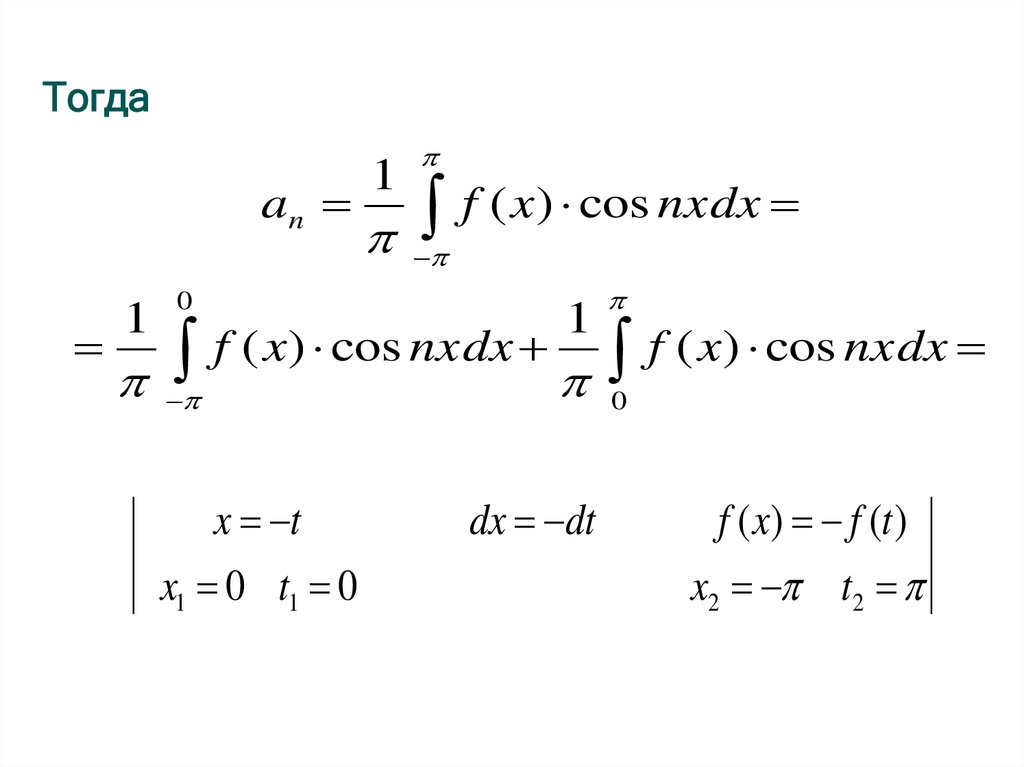
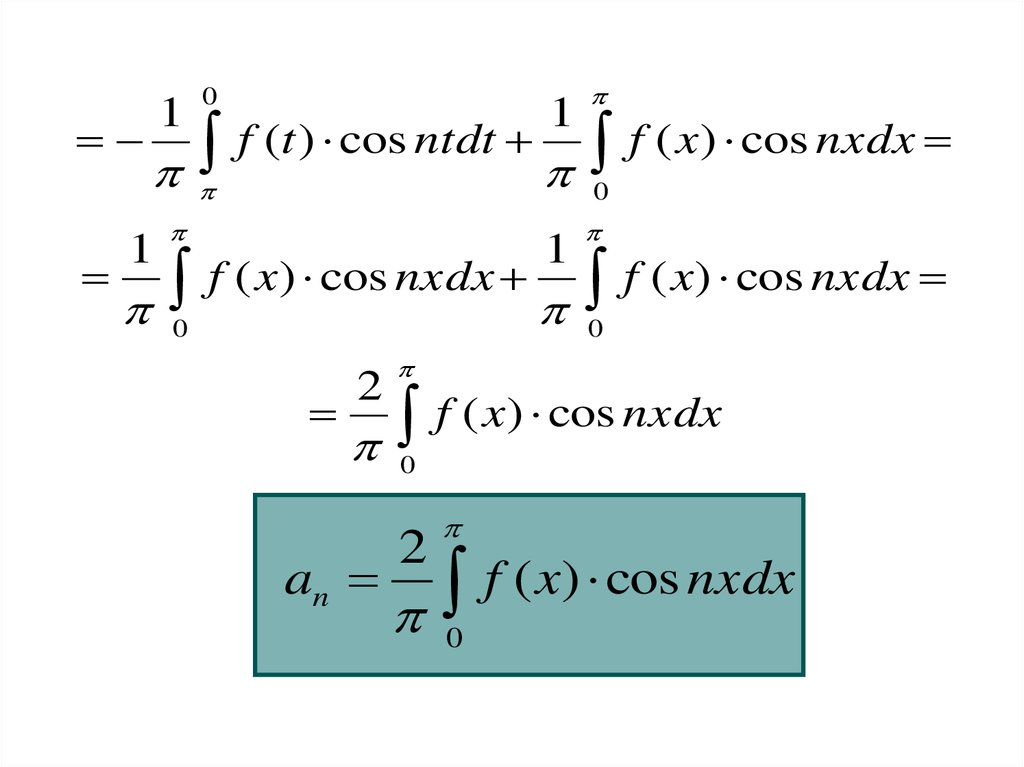












 Математика
Математика








