Похожие презентации:
Положение плоскости в пространстве и на чертеже
1.
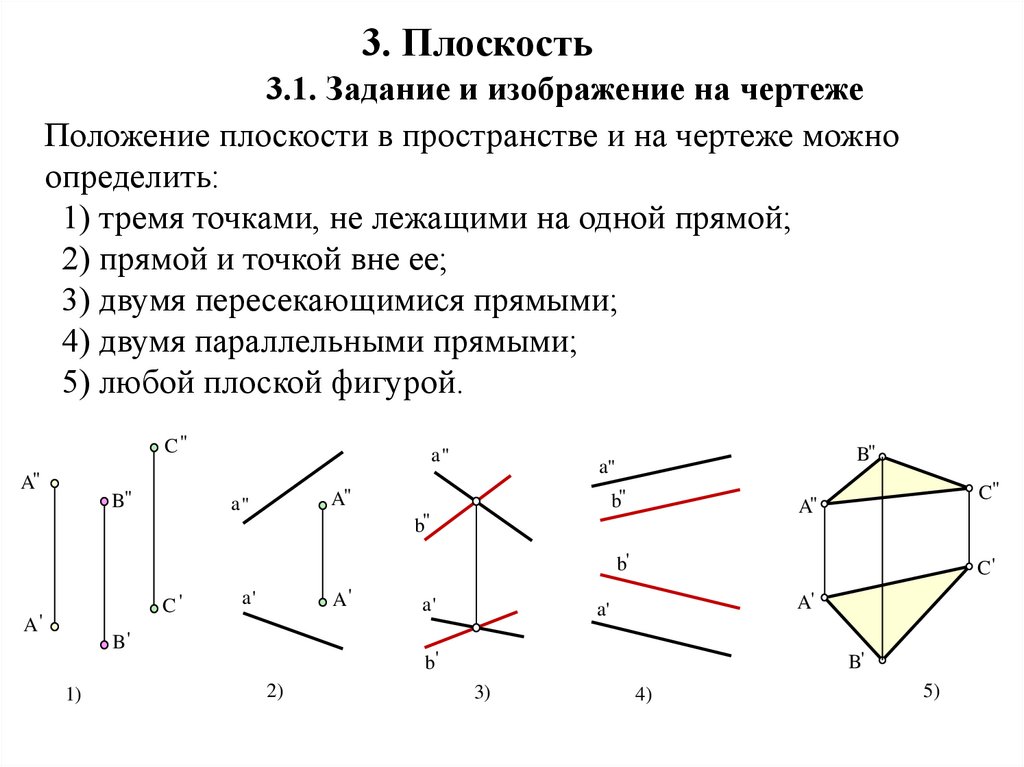
3. Плоскость3.1. Задание и изображение на чертеже
Положение плоскости в пространстве и на чертеже можно
определить:
1) тремя точками, не лежащими на одной прямой;
2) прямой и точкой вне ее;
3) двумя пересекающимися прямыми;
4) двумя параллельными прямыми;
5) любой плоской фигурой.
C"
A"
B"
a"
A"
a"
B"
a"
b"
C"
A"
b"
b'
C'
A'
A'
a'
B'
1)
a'
C'
A'
a'
b'
2)
B'
3)
4)
5)
2.
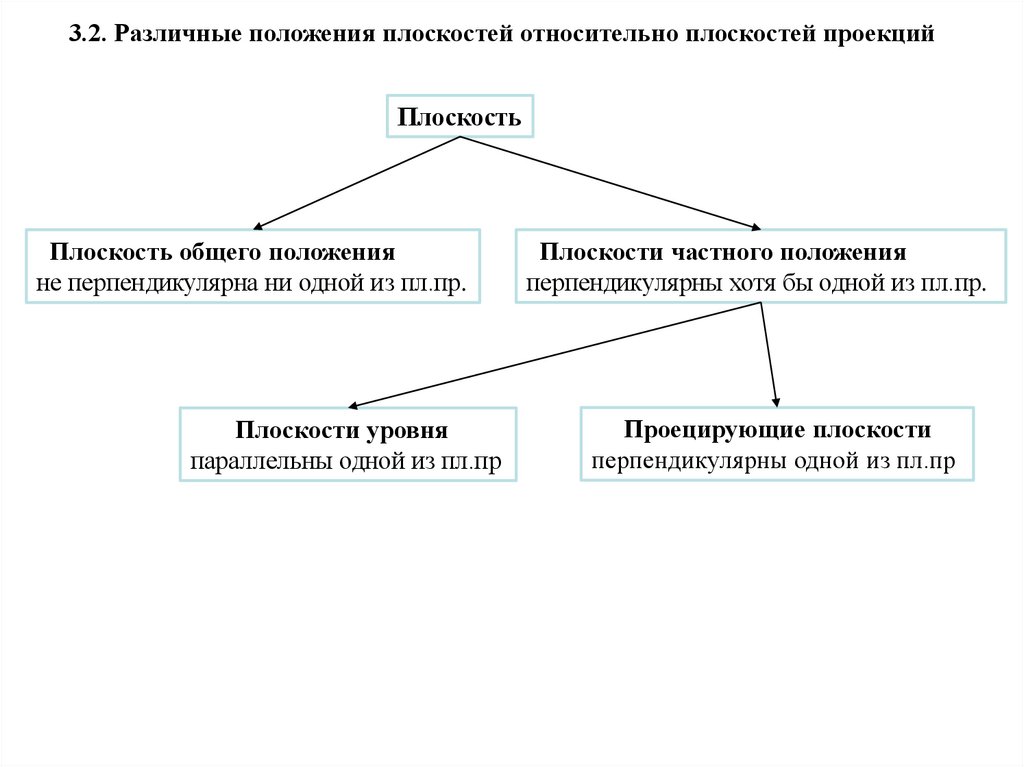
3.2. Различные положения плоскостей относительно плоскостей проекцийПлоскость
Плоскость общего положения
не перпендикулярна ни одной из пл.пр.
Плоскости уровня
параллельны одной из пл.пр
Плоскости частного положения
перпендикулярны хотя бы одной из пл.пр.
Проецирующие плоскости
перпендикулярны одной из пл.пр
3.
Плоскость общего положенияПлоскость, не перпендикулярная ни одной плоскости проекций, называется
плоскостью общего положения. На комплексном чертеже проекции
элементов, задающих плоскость, занимают общее положение (см. рис).
4.
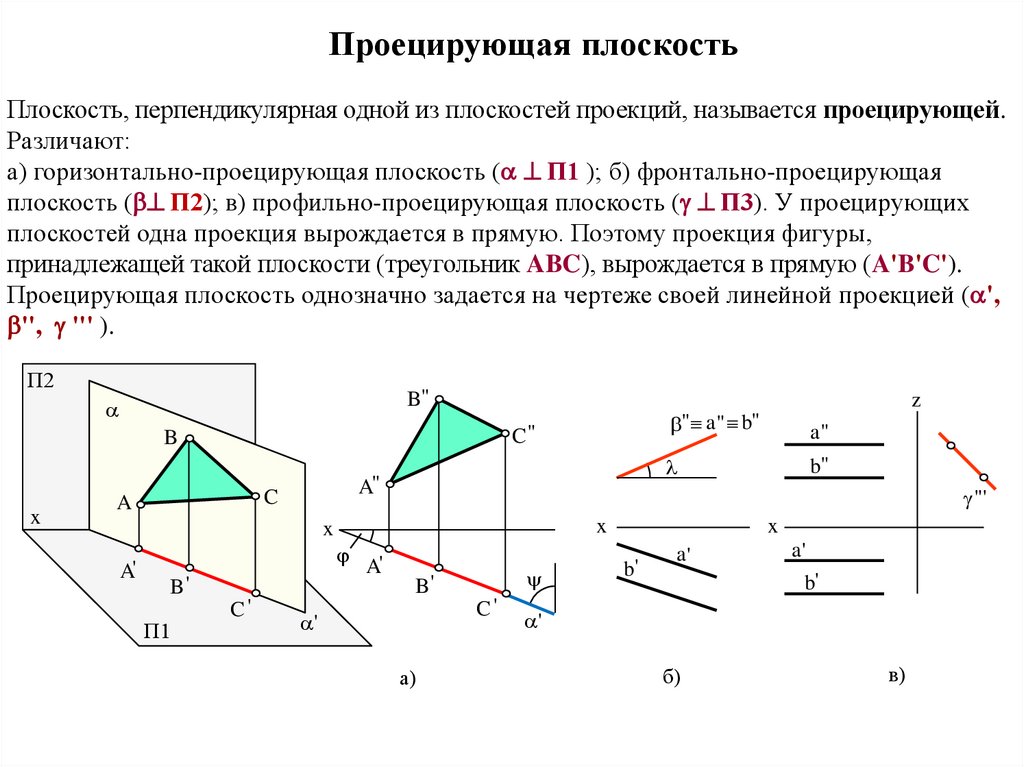
Проецирующая плоскостьПлоскость, перпендикулярная одной из плоскостей проекций, называется проецирующей.
Различают:
a) горизонтально-проецирующая плоскость (a ^ П1 ); б) фронтально-проецирующая
плоскость (b^ П2); в) профильно-проецирующая плоскость (g ^ П3). У проецирующих
плоскостей одна проекция вырождается в прямую. Поэтому проекция фигуры,
принадлежащей такой плоскости (треугольник ABC), вырождается в прямую (A'B'C').
Проецирующая плоскость однозначно задается на чертеже своей линейной проекцией (a',
b'', g ''' ).
П2
B"
a
C"
B
x
A"
C
A
A'
B'
П1
C'
a"
l
b"
g "'
x
x
j
A'
z
_ _
b" _ a" _ b"
y
B'
C'
a'
а)
x
b'
a'
a'
b'
a'
б)
в)
5.
Плоскость уровняПлоскость, параллельная одной из плоскостей проекций, называется
плоскостью уровня.
П2 A"
a"
Различают:
а) горизонтальная плоскость
C"
уровня (a // П1);
a"
б) фронтальная плоскость
уровня (b // П2);
в) профильная плоскость
уровня (g // П3).
Плоскость уровня является
частным случаем проециC'
рующей плоскости (является
дважды проецирующей),
поэтому на чертеже задается
своей линейной проекцией
(a'', b', g '', g ').
g"
Фигура, принадлежащая
плоскости уровня,
проецируется на соответствующую плоскость проекций
g'
в натуральную величину.
B" C"
A"
B
B"
A
C
a
x
x
B'
B'
A'
A'
C'
П1
а)
П2
a"
b"
g
x
x
x
b ' __ a' __ b'
П1
б)
в)
6.
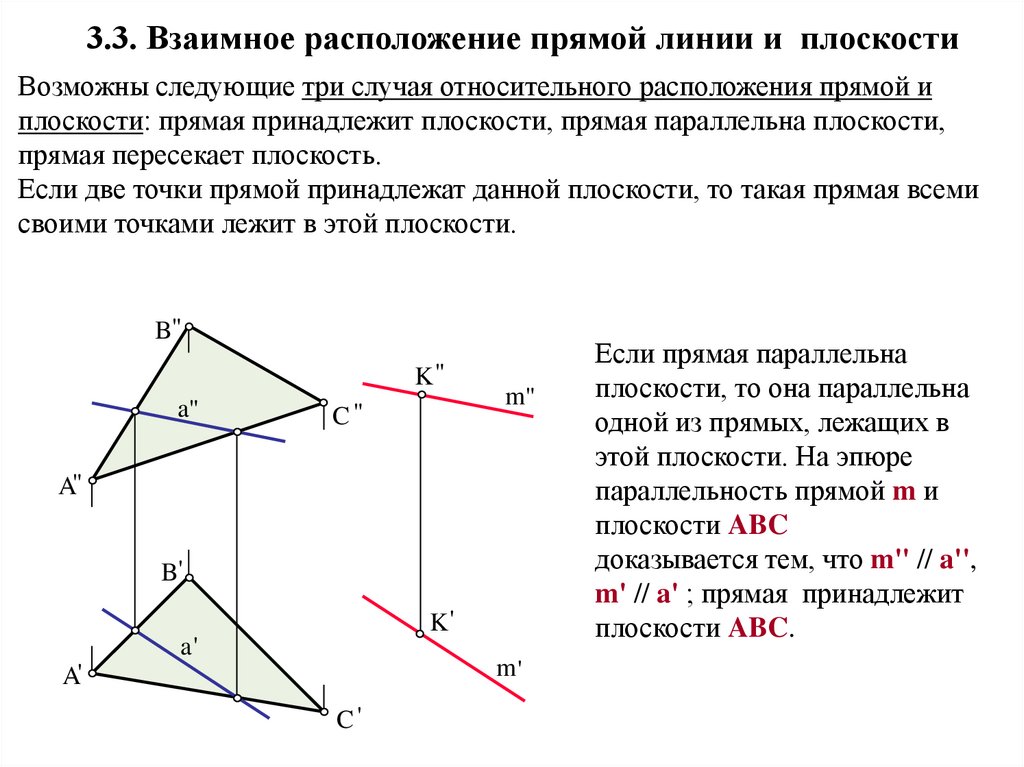
3.3. Взаимное расположение прямой линии и плоскостиВозможны следующие три случая относительного расположения прямой и
плоскости: прямая принадлежит плоскости, прямая параллельна плоскости,
прямая пересекает плоскость.
Если две точки прямой принадлежат данной плоскости, то такая прямая всеми
своими точками лежит в этой плоскости.
B"
K"
a"
C"
m"
A"
B'
K'
a'
m'
A'
C'
Если прямая параллельна
плоскости, то она параллельна
одной из прямых, лежащих в
этой плоскости. На эпюре
параллельность прямой m и
плоскости ABC
доказывается тем, что m'' // a'',
m' // a' ; прямая принадлежит
плоскости ABC.
7.
C"A"
K"
a"
B"
a'
C'
A'
K'
B'
Частные случаи
пересечения прямой и
плоскости:
В первом случае плоскость a
(АВС) – горизонтальнопроецирующая.
Поэтому горизонтальная
проекция К' искомой точки К
определяется как точка
пересечения линейной проекции
А'В'С' плоскости a с
горизонтальной проекцией а'
данной прямой а.
Фронтальная проекция К" точки
К строится из условия
принадлежности точки К прямой а.
8.
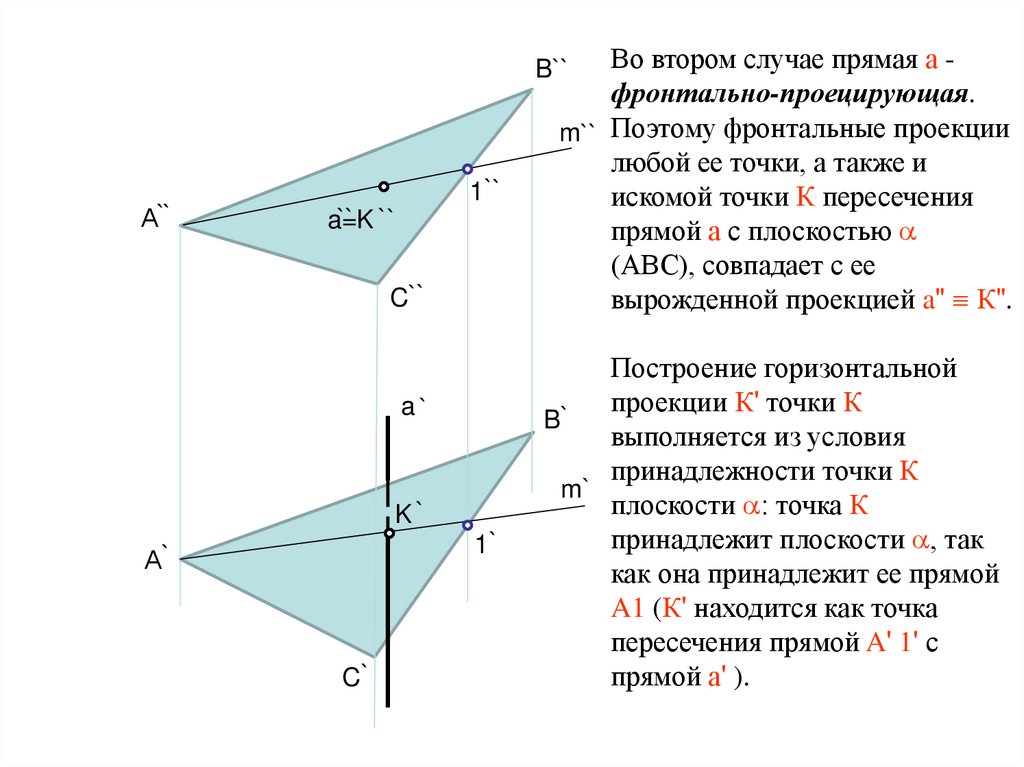
Во втором случае прямая а фронтально-проецирующая.m`` Поэтому фронтальные проекции
любой ее точки, а также и
искомой точки К пересечения
прямой а с плоскостью a
(АВС), совпадает с ее
вырожденной проекцией a" К".
B``
А``
1``
`` ` `
a=K
C``
a`
K`
1`
А`
C`
Построение горизонтальной
проекции К' точки К
B`
выполняется из условия
принадлежности точки К
m`
плоскости a: точка К
принадлежит плоскости a, так
как она принадлежит ее прямой
A1 (К' находится как точка
пересечения прямой A' 1' с
прямой а' ).
9.
Частные случаи пересечения плоскостей1. Плоскость α (ABC) и плоскость β (l //m)
фронтально-проецирующие.
10.
Частные случаи пересечения плоскостей2. Плоскость α (ABC) общего положения,
плоскость β (l //m) горизонтально-проецирующая
.





 Инженерная графика
Инженерная графика








