Непрерывность функции. Лекции 6

1.

НЕПРЕРЫВНОСТЬ
ФУНКЦИИ
Лекции 6

2.

Непрерывность функции в точке.
Непрерывность функции в интервале, на отрезке.
Теорема об арифметических операциях над
непрерывными в данной точке функциями
Предел и непрерывность сложной функции.
Непрерывность обратной функции.
Свойства функции, непрерывной на отрезке.
Равномерная непрерывность функции
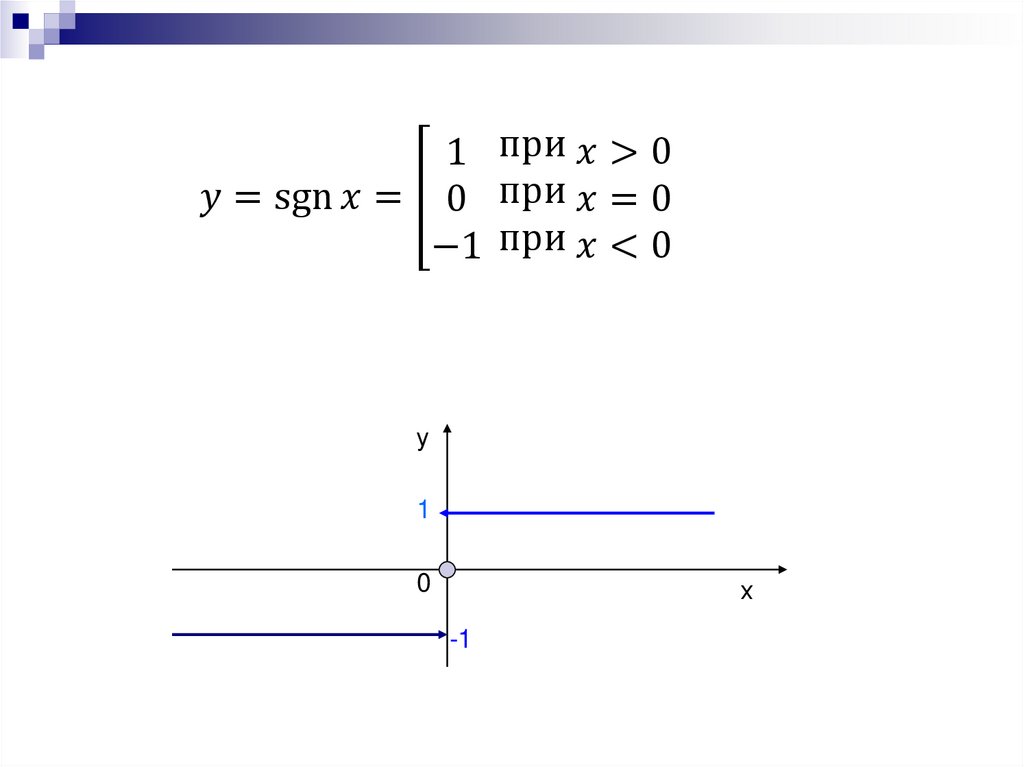
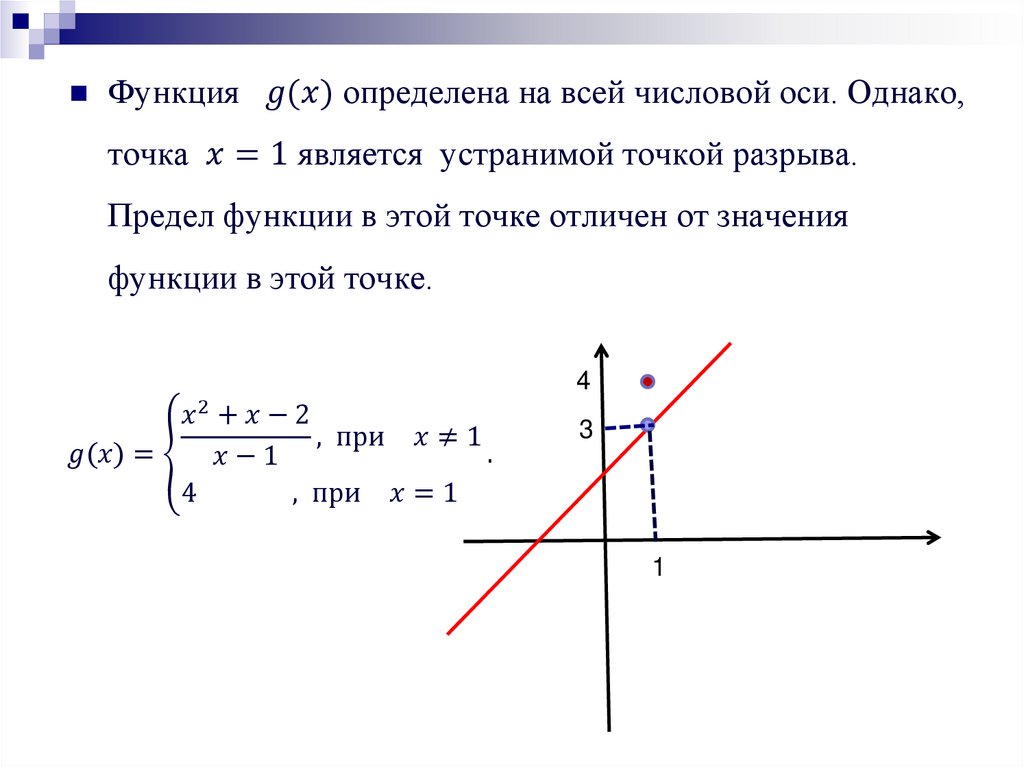
Точки разрыва функции и их классификация.

3.

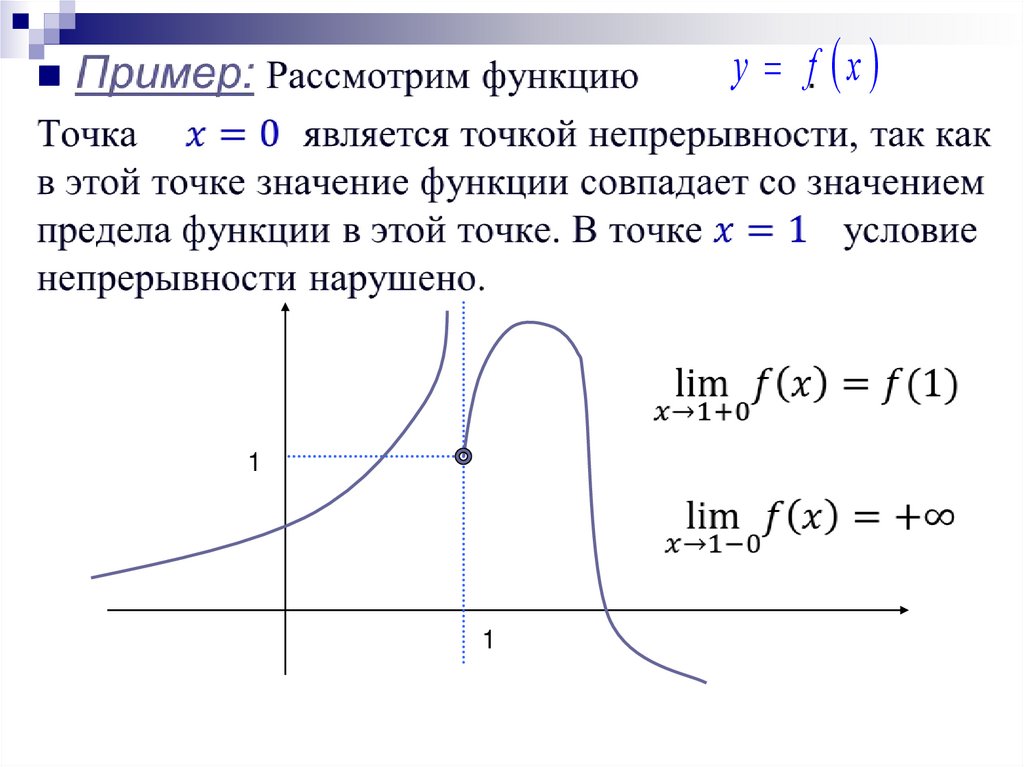
Непрерывность функции.
О п р е д е л е н и е 1. Функция y f x
называется непрерывной в точке a ,
принадлежащей области определения D ( f ) , если
функция y f x имеет в точке a конечный
предел, равный числу f а , то есть
З а м е ч а н и е. Символически равенство (1)
записывают в виде

4.

Непрерывность функции.
y f x
a
D( f )
a
f а

5.

6.

Из свойств предела вытекает следующее
утверждение.
Т е о р е м а 1. Функция
y f x непрерывна
в точке a тогда и только тогда, когда в этой
точке справедливы равенства:

7.

y f x
1
1

8.

Непрерывность функции в интервале, на отрезке.
О п р е д е л е н и е 4. Функция