Похожие презентации:
Непрерывность функции. Непрерывность функции в точке
1. Непрерывность функции
2. Непрерывность функции в точке
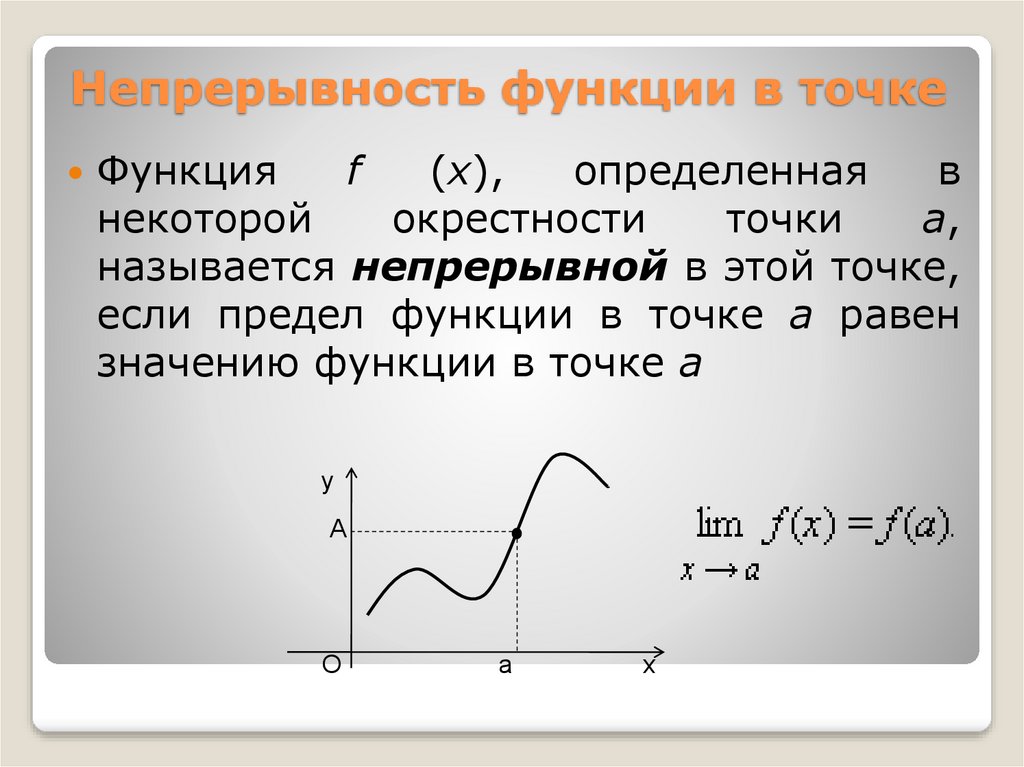
Функцияf
(x),
определенная
в
некоторой
окрестности
точки
a,
называется непрерывной в этой точке,
если предел функции в точке а равен
значению функции в точке а
у
А
О
а
х
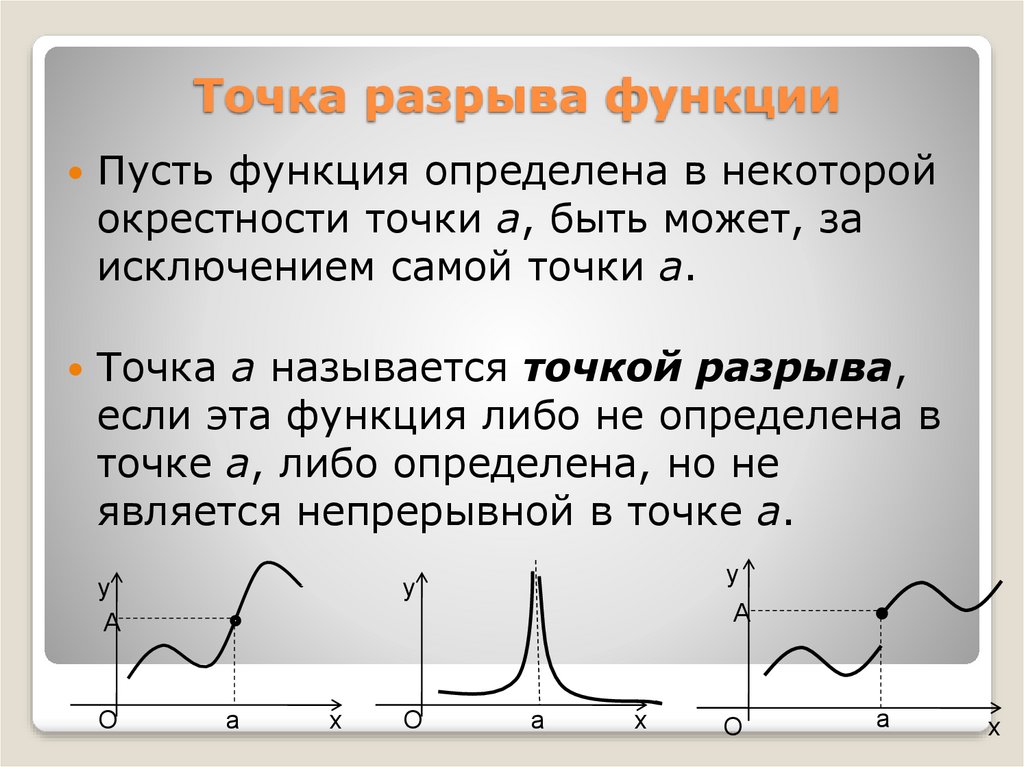
3. Точка разрыва функции
Пусть функция определена в некоторойокрестности точки a, быть может, за
исключением самой точки a.
Точка a называется точкой разрыва,
если эта функция либо не определена в
точке a, либо определена, но не
является непрерывной в точке a.
у
А
О
у
у
а
х
О
А
а
х
О
а
х
4. Таким образом, можно сказать, что функция непрерывна в точке а, если выполнены 3 условия:
1.Функцияопределена в точке а и в некоторой её
окрестности;
2.Функция имеет предел при x → а; lim f(x)=A
3.Этот предел равен значению функции в точке а,
т.е. A=f(a).
Объясните почему функции изображённые на
рисунке не являются непрерывными
y
y
1
o
y
1
x
o
1
x
o
x
5. Непрерывность функции на отрезке
Функцию f (x) называют непрерывнойна отрезке [a; b], если она непрерывна
в каждой точке интервала (a; b) и,
кроме того, непрерывна справа в
точке a и слева в точке b.
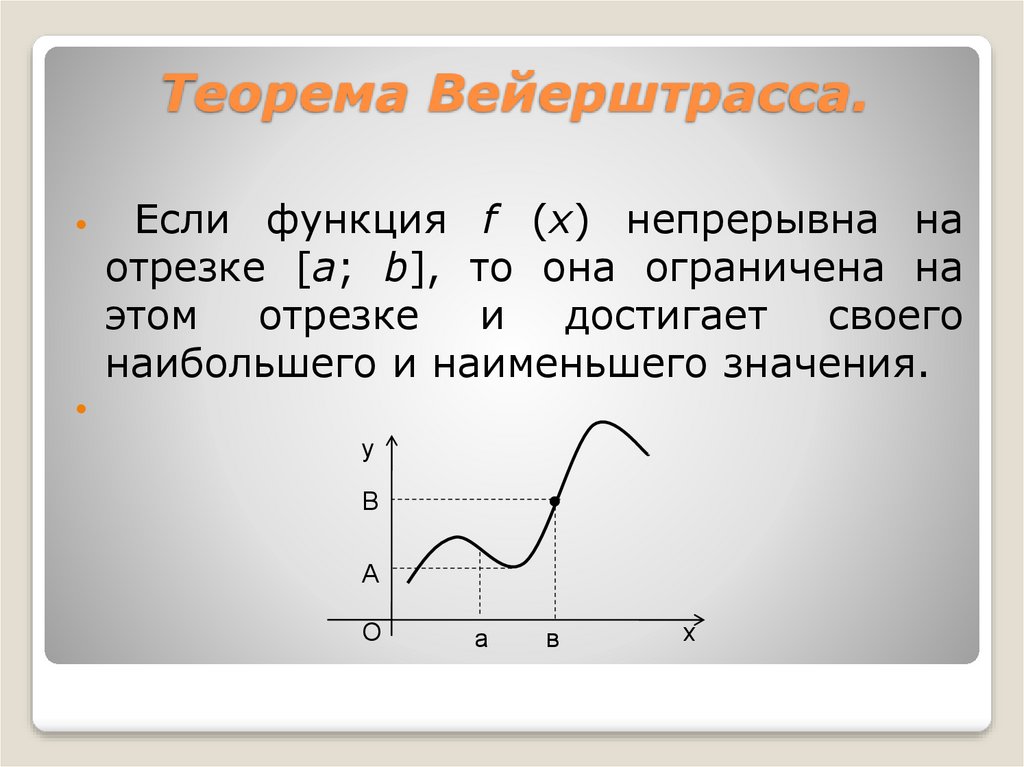
6. Теорема Вейерштрасса.
Если функция f (x) непрерывна наотрезке [a; b], то она ограничена на
этом
отрезке
и
достигает
своего
наибольшего и наименьшего значения.
у
В
А
О
а
в
х
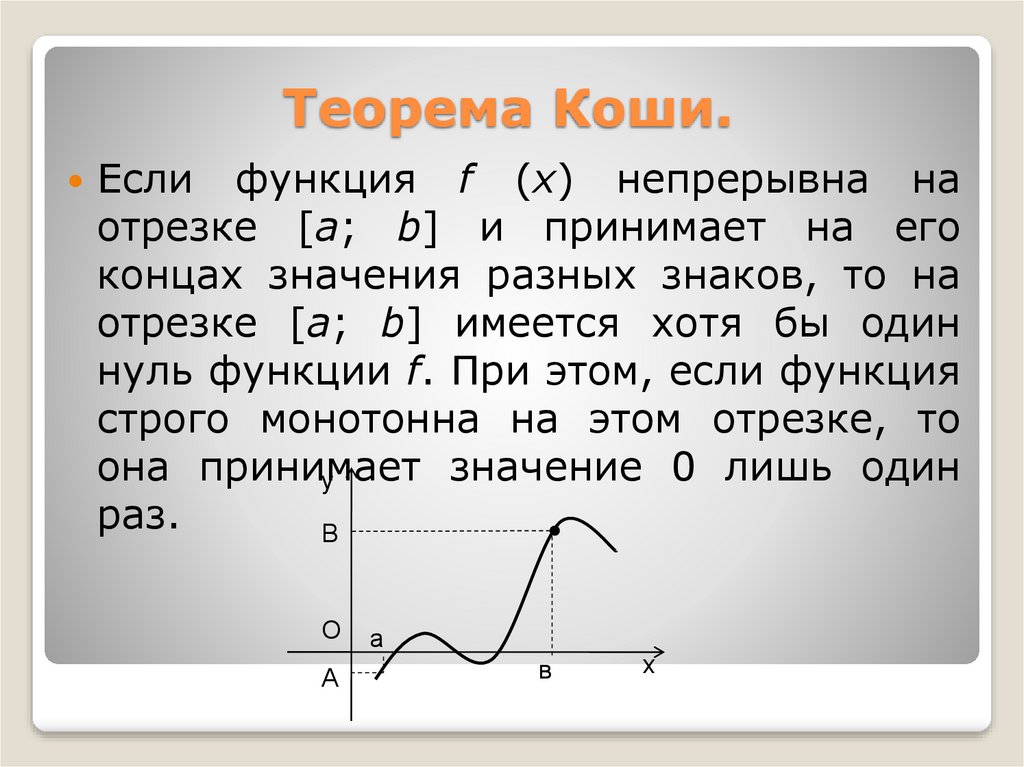
7. Теорема Коши.
Теорема Коши.Если функция f (x) непрерывна на
отрезке [a; b] и принимает на его
концах значения разных знаков, то на
отрезке [a; b] имеется хотя бы один
нуль функции f. При этом, если функция
строго монотонна на этом отрезке, то
она принимает
значение 0 лишь один
у
раз.
В
О
А
а
в
х
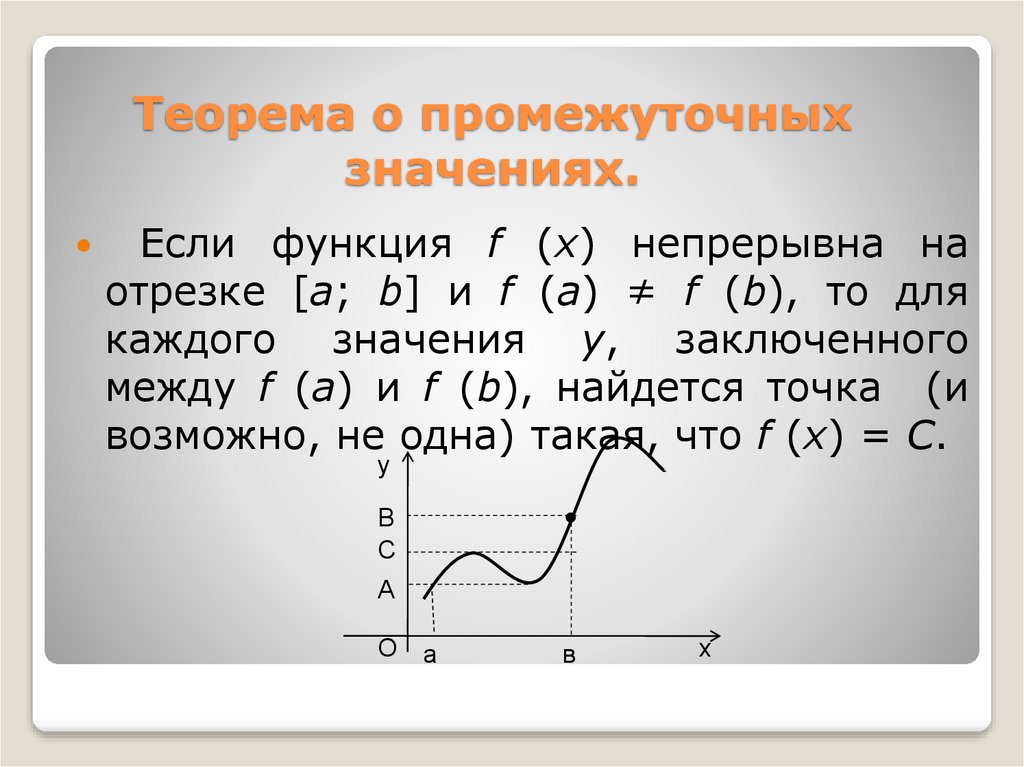
8. Теорема о промежуточных значениях.
Если функция f (x) непрерывна наотрезке [a; b] и f (a) ≠ f (b), то для
каждого значения y, заключенного
между f (a) и f (b), найдется точка (и
возможно, не одна) такая, что f (x) = C.
у
В
C
А
О а
в
х
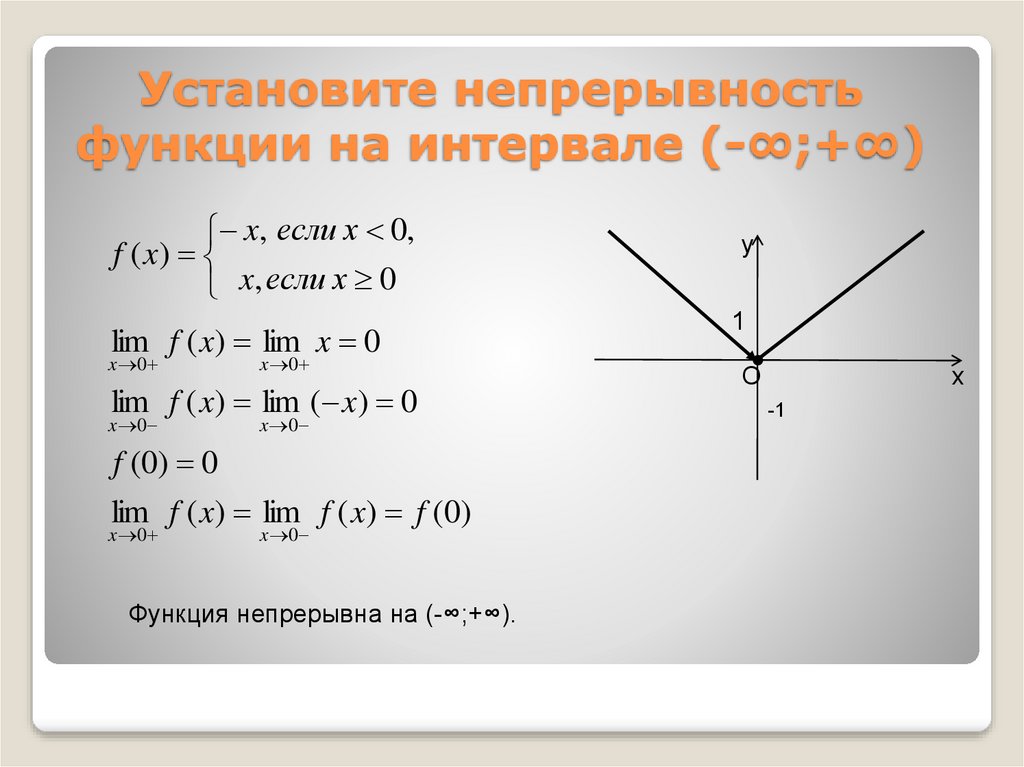
9. Установите непрерывность функции на интервале (-∞;+∞)
x, если х 0,f ( x)
x, если х 0
lim f ( x) lim x 0
x 0
x 0
lim f ( x) lim ( x) 0
x 0
x 0
f (0) 0
lim f ( x) lim f ( x) f (0)
x 0
x 0
Функция непрерывна на (-∞;+∞).
у
1
О
х
-1
10. Установите непрерывность функции на интервале (-∞;+∞)
x, если х 1,f ( x)
x, если х 1
lim f ( x) lim x 1
x 1
x 1
lim f ( x) lim ( x) 1
x 1
x 1
f (1) 1
lim f ( x) lim f ( x)
x 1
x 1
Функция не является непрерывной на (-∞;+∞).
Разрыв в точке х=1
у
1
х
О
-1
11. Установите непрерывность функции на интервале (-∞;+∞)
x 2, если х 2,2
f ( x) x , если 2 х 2,
х 2, если х 2
у
lim f ( x) lim x 2 4
x 2
-2
x 2
lim f ( x) lim ( x 2) 4
x 2
x 2
f ( 2 ) 4
12
х
lim f ( x) lim ( x 2) 0
x 2
x 2
lim f ( x) lim x 2 4
lim f ( x) lim f ( x ) f ( 2)
x 2
О
x 2
x 2
x 2
lim f ( x) lim f ( x)
x 2
x 2
Функция непрерывна в точке х=-2
Функция не является непрерывной на (-∞;+∞).
Разрыв в точке х=2
12. Установите непрерывность функции на интервале (-∞;+∞)
6х , если х 2,
f ( x) х 1, если 2 х 2,
1
, если х 2
х 1
lim f ( x) lim ( х 1) 3
x 2
у
-2
О
1 2
х
x 2
6
3
x 2 х
lim f ( x) lim
x 2
f ( 2) 3
lim f ( x) lim f ( x) f ( 2)
x 2
x 2
Функция непрерывна в точке х=-2
Разрыв в точке х=2, так как функция
в точке х=2 не определена.
Функция не является непрерывной на (-∞;+∞).
13. Установите непрерывность функции на интервале (-∞;+∞)
x 2 3x 5, если x 2f ( x)
4 x 5, если x 2
1
x 4, если x 2
22
f ( x) x 9, если 2 x 2
2 x 1,5, если x 2
x 3, если x 1
f ( x) x 2 x, если 1 x 3
2 x 6, если x 3
0,9 x 5,4, если x 3
f ( x) 4 x 2 , если 3 x 2
2,5 x 5, если x 2







 Математика
Математика








