Задача о вычислении мгновенной скорости s ( t ) = 4 t²

1.

Задача о вычислении мгновенной скорости
s ( t ) = 4 t² - закон движения материальной
точки по прямой
s - путь, пройденный за время t (t ≥ 0)
Вычислим v ср - среднюю скорость точки за
промежуток времени от t 1 = 2 до t 2 = 5
s (5) = 4 · 5² = 100;
s (2) = 4 · 2² = 16;
s (5) ̶ s (2) = 100 – 16 = 84;
t 2 - t 1 = 5 – 2.
s 5 s 2 84
28.
vср
3
5 2

2.

Задача о вычислении мгновенной скорости
s(t)=4t²
Вычислим v ср
за промежуток времени от t до t + Δ t
s (t + Δ t) = 4 (t + Δ t)² ;
s (t) = 4 t ²;
Δ s = s (t + Δ t) ̶ s (t) – путь, пройденный
точкой за промежуток времени от t до t + Δ t
Δ s = 4 (t + Δ t)² - 4 t ² = (8 t + 4Δ t) Δ t ;
s 8t 4 t t 8t 4 t.
vср
t
t

3.

Общий случай:
точка движется по прямой по закону s(t) = f (t)
Тогда её мгновенной скоростью v в момент
времени t называют предел (если он существует),
к которому стремится её средняя скорость на
промежутке времени [t; t + Δt] при Δ t → 0 :
f
lim
.
v =Δlim
v
=
ср
t→0
Δ t → 0 t
Величина Δ t – приращение времени
Величина Δ f = f(t + Δt) – f(t) - приращение пути
f
v = Δlim
.
t→0
t

4.

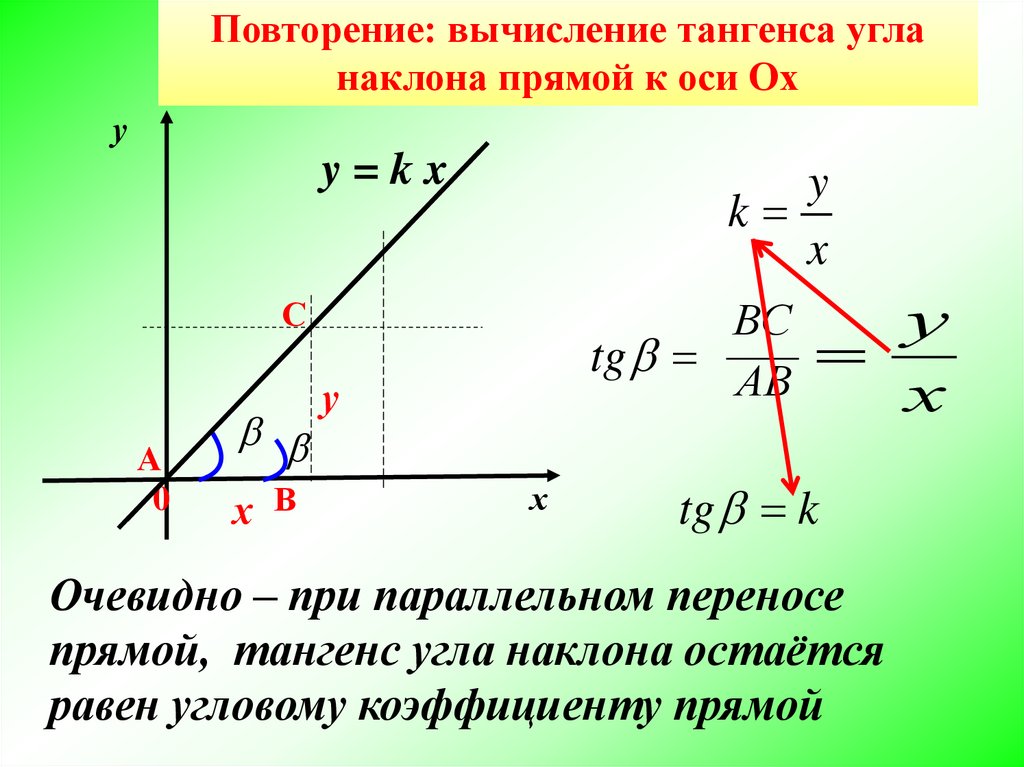
Повторение: вычисление тангенса угла
наклона прямой к оси Ох
у
y=kx
y
k
x
ВС
у
tg
АВ
х
С
А
0
х В
у
х
tg k
Очевидно – при параллельном переносе
прямой, тангенс угла наклона остаётся
равен угловому коэффициенту прямой

5. Касательной к графику функции f(x) в точке А( х; f (х) ) называется прямая, представляющая предельное положение секущей АС,

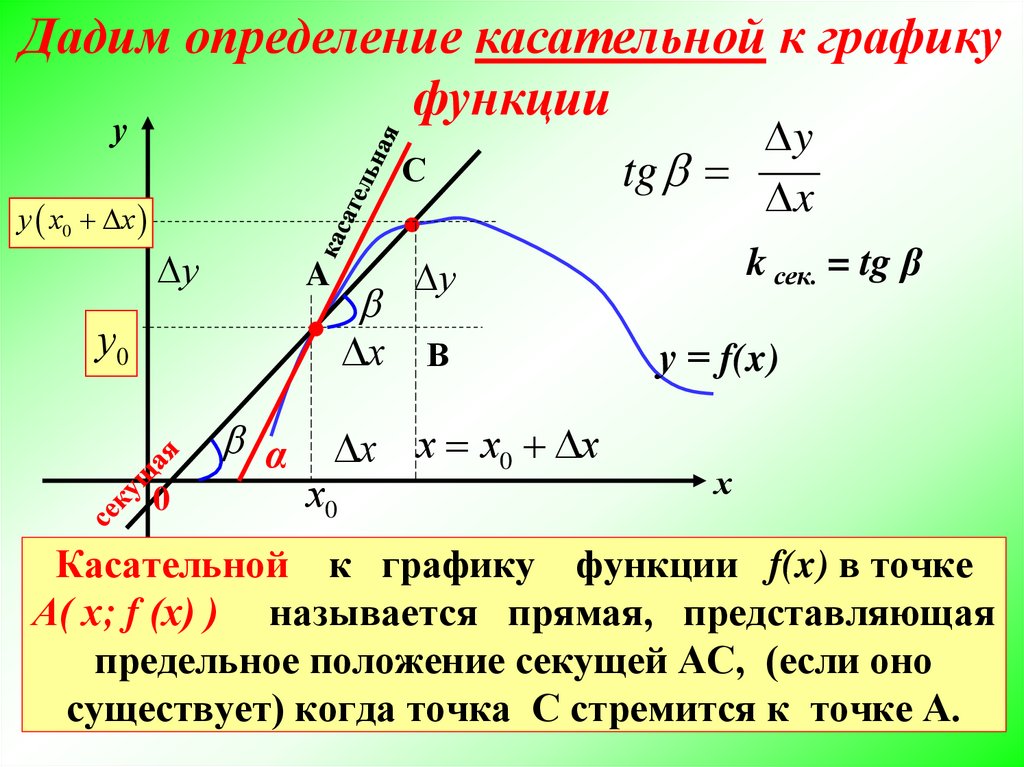
Дадим определение касательной к графику
функции
у
y
С
tg
x
у х0 х
у
A
х
у0
α
0
В
х х х0 х
х0
k сек. = tg β
у
у = f(x)
х
Касательной к графику функции f(x) в точке
А( х; f (х) ) называется прямая, представляющая
предельное положение секущей АС, (если оно
существует) когда точка С стремится к точке А.

6.

Задача о вычислении тангенса угла
наклона
касательной
к
графику
функции
y
y f (x )
tg
y
x
= k сек.
y
y
0
х0
х х
х
х
у
При
Δ
х
→
0
угловой
коэффициент
секущей
(k
)
сек.
kкас.
=
lim
k
=
lim
lim
tg
β
=
tg
α
Секущая стремится
занять положение касательной.
сек.
Δ х →к
0 угловому
Δ хΔ→
0
х Δх→ 0
х→
0 коэффициенту
стремится
То есть, касательная есть предельное положение секущей.
касательной (kкас. )

7.

Задача о
вычислении
мгновенной
скорости
f
v = Δlim
.
t→0
t
Задача о вычислении
тангенса угла наклона
касательной к графику
функции
у k
tg α = lim
кас.
Δх→ 0 х
В каждой из задач надо было найти предел
отношения приращения функции к
приращению аргумента, при условии, что
приращение аргумента стремится к нулю

8.

Определение
производной

9.

10.

Тайны планетных орбит.
Древнегреческие учёные умели решать немногие
задачи кинематики – рассчитать либо
равномерное прямолинейное движение, либо
равномерное вращение вокруг оси.
А планеты на небосводе двигались по самым
замысловатым кривым . Свести эти движения
планет к простым древним учёным не удавалось.
Лишь в 17 веке немецкому учёному Иоганну
Кеплеру удалось сформулировать законы
движения планет. Оказалось, что планеты
движутся по эллипсам, и притом неравномерно.
Объяснить, почему это так, Кеплер не смог.

11.

В конце 17 века Исаак Ньютон открыл законы
динамики, сформулировал закон всемирного
тяготения и развил математические методы,
позволявшие сводить неравномерное к
равномерному, неоднородное к однородному,
криволинейное к прямолинейному.
В основе лежала простая идея – движение
любого тела за малый промежуток времени можно
приближённо рассматривать как прямолинейное и
равномерное.
Одновременно с Ньютоном немецкий
философ и математик Готфрид Вильгельм
Лейбниц изучал, как проводить касательные к
произвольным кривым.

12.

Он также развил новое исчисление, которое
оказалось по сути дела тождественным
построенному Ньютоном. Обозначения, введённые
Лейбницем, оказались настолько удачными, что
сохранились и по сей день.
Новая математика Ньютона и Лейбница
состояла из двух больших частей –
дифференциального и интегрального исчислений.
В первом из них говорилось, как, изучая
малую часть явления, сводить неравномерное к
равномерному.
Во второй – как из малых равномерных
частей конструировать сложное неравномерное
явление.

13.

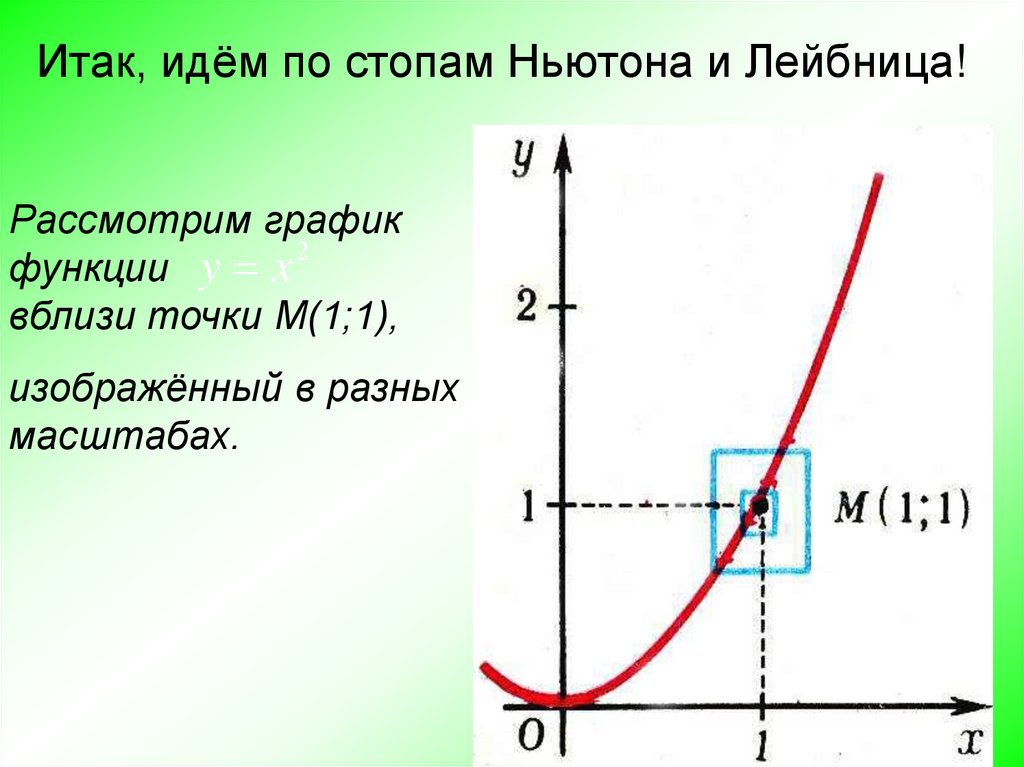
Итак, идём по стопам Ньютона и Лейбница!
Рассмотрим график
2
функции y x
вблизи точки М(1;1),
изображённый в разных
масштабах.

14.

Как изменилась
конфигурация
графика?

15.

Определите радиус
окрестности
точки х = 1
Как изменилась
конфигурация
графика?

16.

Основные выводы
1. Чем крупнее масштаб, тем меньше график
функции будет отличаться от некоторой
прямой, проходящей через точку М(1;1).
2. То же самое будет происходить с
графиком функции вблизи любой другой
точки.
3. Этим свойством обладают и многие
другие кривые: окружность, гипербола,
синусоида и т. д.
Такое свойство функций называют
«линейность в малом»

17.

• Пусть точка движется вдоль
прямой по закону S(t).
Тогда за промежуток времени t
точка проходит расстояние S(t).
Пусть ∆t – малый промежуток
времени. Путь, пройденный за
время t+ ∆t, равен S(t+ ∆t ).
Тогда средняя скорость
S (t t ) S (t )
vср .
t

18.

• Очевидно, если ∆t
0, то Vср.
Значит,
S (t t ) S (t )
v м гн. lim
Vмгн.
t
S
или v м гн. lim
,
t 0 t
где t приращение времени
S - приращение пути.
t 0

19.

x
x
x0 - ∆x
х0
x0 + ∆x
х
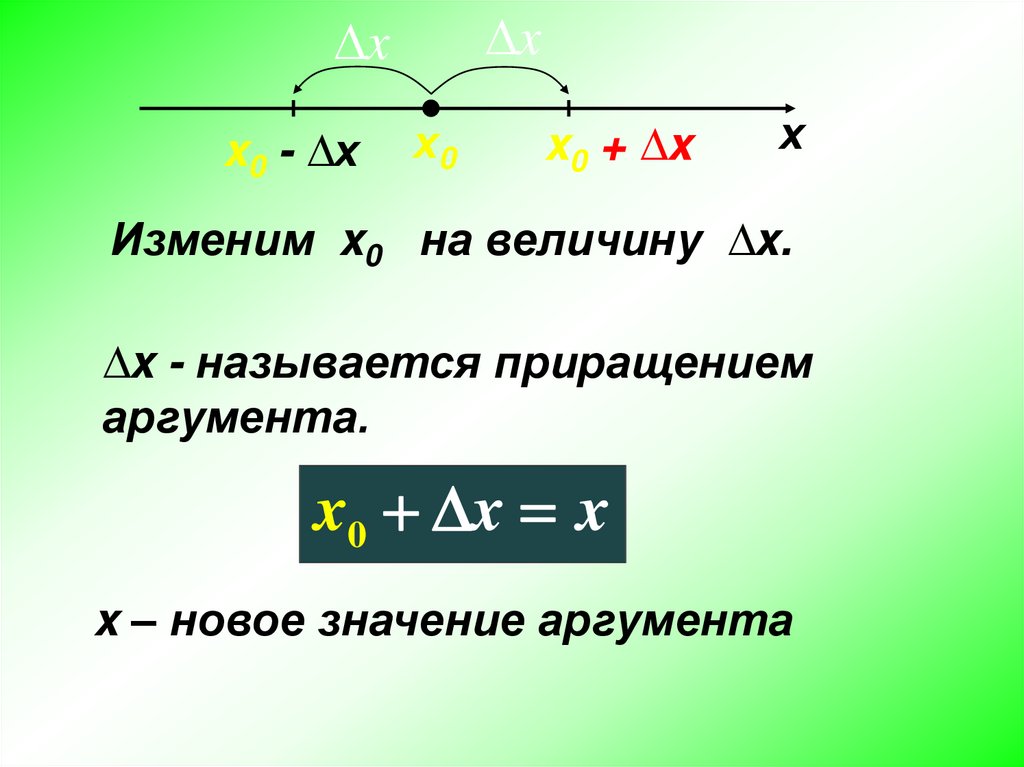
Изменим x0 на величину ∆x.
∆x - называется приращением
аргумента.
x0 x x
x – новое значение аргумента

20.

Величина y(x) – y(x0)
называется приращением функции
в точке x0 и обозначается ∆y(x0) .
y x0 y x0 x y x0

21.

Таким образом, чтобы вычислить
приращение функции f(x) при переходе от
точки x0 к точке x = x0 + Δx , нужно:
1. найти значение функции f(x0);
2. найти значение функции f(x0 + Δx)
3. найти разность f(x0 + Δx) – f(x0)

22.

В математике операция нахождения предела
отношения приращения функции Δ f к
приращению аргумента Δ x , при условии, что
приращение Δ x → 0 называется -
дифференцирование функции
Результат выполнения называют
производной и обозначают: f x
f
f '(x)= lim
.
Δ х → 0 х

23.

Определение производной
Производной функции в точке x
называется предел отношения приращения
функции в этой точке (∆f) к
соответствующему приращению аргумента
(∆x), когда приращение аргумента
стремится к нулю

24.

Определение производной
Производной функции f ( x) в точке х0
называется число, к которому стремится
f
отношение
при х 0.
x

25.

Чтобы найти производную функции в
точке, надо:
1. найти приращение функции в точке Хx00
;
2. найти отношение приращения функции к
приращению аргумента;
3. вычислить предел полученного отношения
при условии, что приращение аргумента
стремится к нулю.

26.

Пример нахождения производной
Дано : f ( x ) x 2 1.
Нати f ( x ).
Решение
f x0 х02 1
f ( x) f ( x0 x) f ( x0 )
f ( x0 x ) ( х 0 x ) 1 х0 2 х0 x x 1
2
2
2
х
f ( x ) х0 2 х0 x x 1 0 1
2
2
х0 2 х0 x x 1 х0 1 x 2 х0 x
2
2
2
f ( x ) x 2 х0 x
2х0 x
x
x
f ( x )
Если x 0, то
2 х0 x 2 х0
x
Значит, f x 2 x.
2

27. Механический смысл производной

s
vмг. (t) = lim
Δt→ 0
t
Механический смысл производной состоит в
том, что производная пути по времени равна
мгновенной скорости в момент времени t0:
S'(t)= Vмг(t)

28. Геометрический смысл производной.

Производная функции в точке x0 равна
угловому коэффициенту касательной к
графику функции y = f(x) в этой точке.
f x0 tg k