Похожие презентации:
Основні співвідношення між тригонометричними функціями одного аргументу
1.
2.
Дуже часто при розв'язуванні задач виникаєпроблема: знайти значення
тригонометричних функцій, якщо задано
лише значення однієї з них. Отже, на даному
уроці ми згадаємо вже відому вам формулу –
основну тригонометричну тотожність - і
виведемо ще декілька формул, які пов'язують
тригонометричні функції одного і того самого
аргументу.
3.
1. Співвідношення між синусом і косинусом.З основної тригонометричної тотожності
sin2 α + cos2 α = l
можна виразити sin α через cos α і навпаки :
sin 1 cos
2
cos 1 sin
2
4.
2. Співвідношення між тангенсом і котангенсом.Згідно з визначенням тангенса і котангенса:
.
.
sin
tg
cos
сos
ctg
sin
Перемноживши ці рівності, одержимо:
tg ctg
Отже,
sin cos
1
cos sin
tg ctg 1
Із одержаної рівності можна виразити tg α через ctg α і навпаки:
1
tg
сtg
1
ctg
tg
5.
3. Співвідношення між тангенсом і косинусом,;
котангенсом
і синусом.
.
.
1) Розділимо ліву і праву частину рівності
соs2 α +sіn2 α = 1 на соs2α,
вважаючи, що соs2α ≠ 0, одержимо:
cos 2 sin 2
1
cos 2
cos 2
звідси:
.
cos 2 sin 2
1
cos 2 cos 2 cos 2
,
1
1 tg
cos 2
2
, де
2
k , k Z .
2) Розділимо ліву і праву частину рівності соs2 α +sіn2 α = 1 на sіn2 α,
вважаючи, що sіn α ≠ 0, одержимо:
,
cos 2 sin 2
1
sin 2
sin 2
звідси:
cos 2 sin 2
1
sin 2 sin 2 sin 2
,
1
1 ctg
sin 2
2
, де
k , k Z .
6.
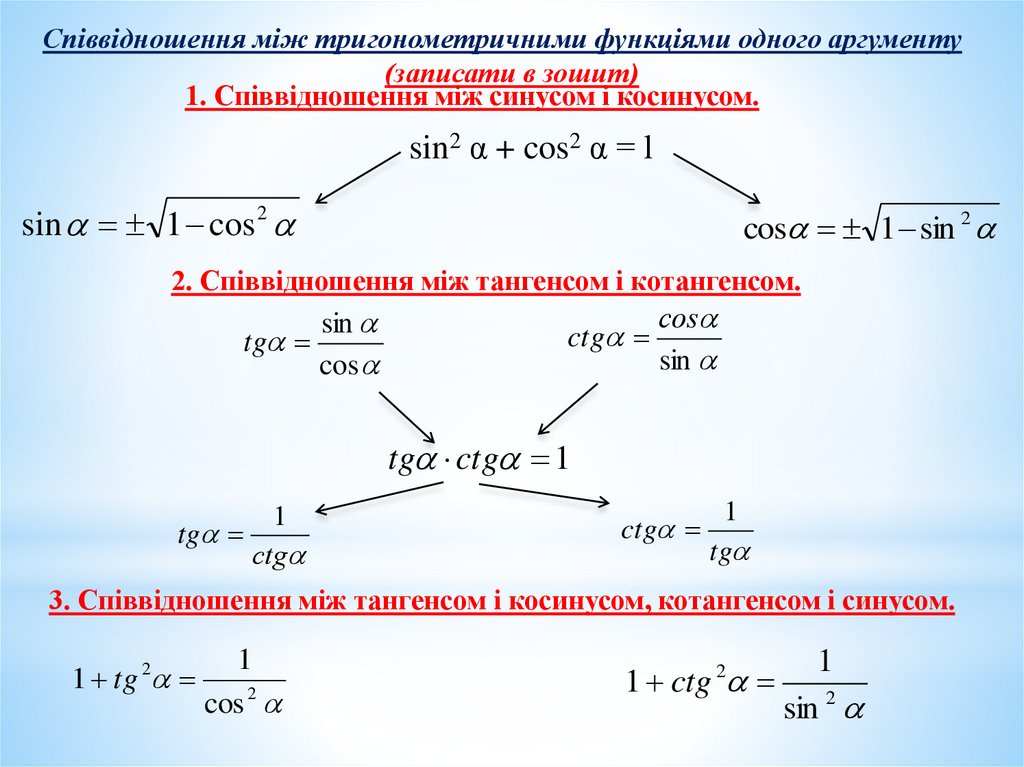
Співвідношення між тригонометричними функціями одного аргументу(записати в зошит)
1. Співвідношення між синусом і косинусом.
sin2 α + cos2 α = l
sin 1 cos 2
cos 1 sin 2
2. Співвідношення між тангенсом і котангенсом.
сos
sin
ctg
tg
sin
cos
tg ctg 1
1
tg
сtg
ctg
1
tg
3. Співвідношення між тангенсом і косинусом, котангенсом і синусом.
1 tg 2
1
cos 2
1
1 ctg
sin 2
2





 Математика
Математика








