Однофакторный регрессионный анализ. Лекция №4

1.

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ
КАФЕДРА КОМПЬЮТЕРНЫХ ТЕХНОЛОГИЙ И ПРОГРАММНОЙ ИНЖЕНЕРИИ
Учебная дисциплина
«ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ»
Лекция №4. Однофакторный регрессионный анализ
Учебные вопросы:
1.
2.
3.
4.
5.
Формулировка задачи построения уравнения регрессии методом
наименьших квадратов.
Скалярная форма построения уравнения регрессии.
Матричная форма построения уравнения регрессии.
Проверка адекватности уравнения регрессии экспериментальным данным
по критерию Фишера.
Проверка значимости коэффициентов регрессии по критерию Стъюдента.
Лектор: доцент 43 кафедры Мышко В.В.

2.

1. Формулировка задачи построения уравнения регрессии методом наименьших квадратов.
Регрессионный анализ – совокупность статистических методов обработки
экспериментальных данных, позволяющих в условии стохастической
зависимости исследуемой величины от неслучайных или случайных
переменных определять данную зависимость.
Термин «стохастическая» здесь означает не полностью определенная,
характеризующаяся недостатком информации.
Результатом регрессионного анализа является математическая конструкция,
которая называется уравнением регрессии или регрессионной зависимостью.
2

3.

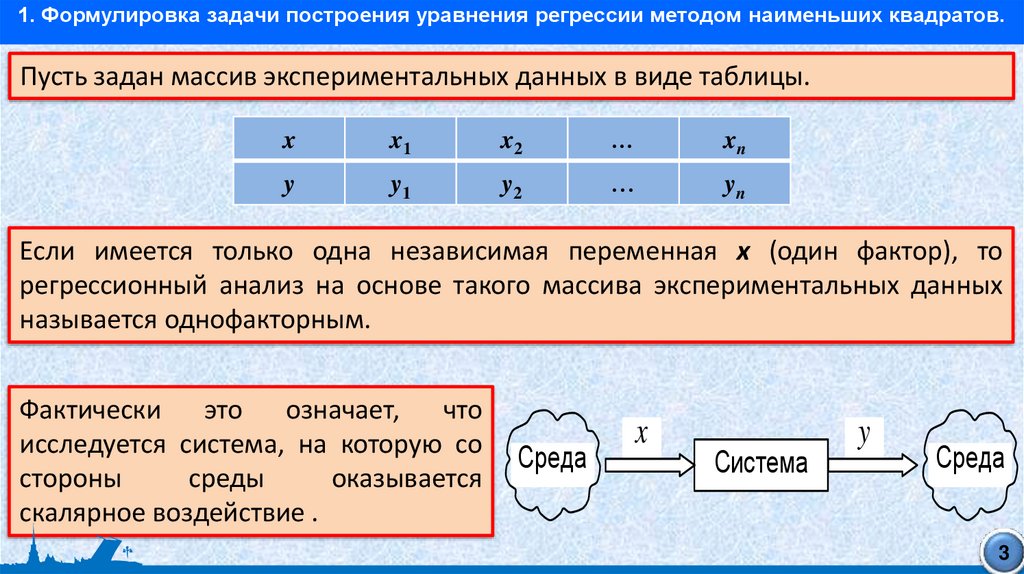
1. Формулировка задачи построения уравнения регрессии методом наименьших квадратов.
Пусть задан массив экспериментальных данных в виде таблицы.
x
x1
x2
…
xn
y
y1
y2
…
yn
Если имеется только одна независимая переменная х (один фактор), то
регрессионный анализ на основе такого массива экспериментальных данных
называется однофакторным.
Фактически
это
означает,
что
исследуется система, на которую со
стороны
среды
оказывается
скалярное воздействие .
Среда
x
Система
y
Среда
3

4.

1. Формулировка задачи построения уравнения регрессии методом наименьших квадратов.
Этапы регрессионного анализа
1. Построение уравнения регрессии.
2. Проверка адекватности (соответствия) уравнения регрессии
экспериментальным данным по критерию Фишера.
3. Проверка значимости коэффициентов регрессии по критерию Стъюдента.
4. Определение окончательного вида уравнения регрессии в зависимости от
значимости коэффициентов.
4

5.

1. Формулировка задачи построения уравнения регрессии методом наименьших квадратов.
Пусть из каких-либо соображений выбран вид аппроксимирующей функции
y f (x)
(1)
Функция (1) определяется не только своим аргументом x, но и своими
параметрами a0 , a1 , ...,ak
y f (x; a0 , a1, ...,ak )
(2)
Универсальным методом построения уравнений регрессии является метод
наименьших квадратов. Для его реализации должна быть сформирована функция
n
V yi f (xi ; a0 , a1, ...,ak )
2
(3)
i 1
в виде суммы квадратов отклонений экспериментальных значений yi зависимой
переменной от теоретических f (xi ; a0 , a1 , ...,ak ) .
5

6.

1. Формулировка задачи построения уравнения регрессии методом наименьших квадратов.
Существо метода наименьших квадратов состоит в выборе таких значений
параметров a0 , a1 , ...,ak , чтобы выполнялось условие
n
2
*
V min yi f (xi ; a0 , a1, ...,ak )
a j R
i 1
j 0, k
(4)
Соотношение (4) указывает, что требуется найти минимально возможное
значение суммы квадратов отклонений экспериментальных значений
зависимой переменной от теоретических. При этом данный минимум
находится подбором параметров на множестве вещественных чисел ( a j R )
6

7.

2. Скалярная форма построения уравнения регрессии.
Рассмотрим наиболее распространенный и универсальный случай, когда
функция регрессии (2) является линейной относительно оцениваемых
параметров:
k
y f (x; a0 , a1 ,...,ak ) a0 f 0 (x) a1 f1 (x) ... ak f k (x ) a j f j (x )
(5)
j 0
где f j (x) , j 0, k – базисные функции, явный вид которых известен.
Параметры aj в выражении (5) называются коэффициентами регрессии.
7

8.

2. Скалярная форма построения уравнения регрессии.
В качестве частного случая (5) можно привести алгебраический полином k-й
степени:
y a0 x n a1x n 1 ... ak 1x ak
(6)
Сопоставляя структуру выражений (5) и (6), нетрудно заметить, что
f 0 (x ) = x n , f1 (x) x n 1 , f k 1 (x ) = x , …, f k (x) 1
(7)
Если в качестве функции регрессии применяется (5), условие (4) принимает вид
n
2
V min yi (a0 f 0 (xi ) a1 f1 (xi ) ... ak f k (xi ))
a j R
i 1
j 0, k
*
(8)
Для нахождения коэффициентов aj
применяется необходимое условие
экстремума функции многих переменных (в данном случае (k+1)-й переменной).
8

9.

2. Скалярная форма построения уравнения регрессии.
Сущность необходимого условия экстремума функции многих переменных:
если функция имеет в точке экстремум, то частные производные от этой
функции в данной точке по всем переменным равны нулю.
Частные производные функции V:
2
k
k
n
n
yi a j f j (xi )
yi a j f j (xi )
i 1
n
k
i 1
j 0
j 0
2 yi a j f j (xi )
a j
a
i 1
j 0
j
k
n
k
2 yi a j f j (xi ) ( f j (xi )) 2 yi a j f j (xi ) f j (xi )
i 1
j 0
i 1
j 0
n
(9)
n
2 yi a0 f 0 (xi ) a1 f1 (xi ) ... ak f k (xi ) f j (xi ).
i 1
9

10.

2. Скалярная форма построения уравнения регрессии.
В выражении (9) использованы правила дифференцирования сложной функции
многих переменных. Поскольку частная производная (9) приравнивается к
нулю, то
n
2 yi (a0 f 0 (xi ) a1 f1 (xi ) ... ak f k (xi )) f j (xi ) 0
(10)
i 1
Обе части уравнения (10) разделим на –2 и, таким образом, получим:
n
yi a0 f0 ( xi ) a1 f1( xi ) ... ak f k ( xi ) f j ( xi ) 0
(11)
i 1
10

11.

2. Скалярная форма построения уравнения регрессии.
Далее в выражении (11) выполняется почленное суммирование, слагаемые,
содержащие yi переносятся в правую часть, затем умножается на –1 обе части
данного равенства:
n
n
n
n
a0 f 0 (xi )f j (xi ) a1 f1 (xi )f j (xi ) ... ak f k (xi )f j (xi ) yi f j (xi )
i 1
i 1
i 1
(12)
i 1
11

12.

2. Скалярная форма построения уравнения регрессии.
Если в выражение (12) подставлять поочередно j 0, 1, 2,...,k , формируется
система уравнений:
n
n
n
n 2
a0 f 0 (xi ) a1 f1 (xi )f 0 (xi ) ... ak f k (xi )f 0 (xi ) yi f 0 (xi );
i 1
i 1
i 1
i 1
n
n
n
n
2
a0 f 0 (xi )f1 (xi ) a1 f1 (xi ) ... ak f k (xi )f1 (xi ) yi f1 (xi );
i 1
i 1
i 1
i 1
n
n
n
n
2
a0 f 0 (xi )f k (xi ) a1 f1 (xi )f k (xi ) ... ak f k (xi ) yi f k (xi ).
i 1
i 1
i 1
i 1
(13)
12

13.

2. Скалярная форма построения уравнения регрессии.
Уравнения (13) представляют собой систему линейных уравнений относительно
параметров a0 , a1 ,..., ak . Следовательно, она решается любым из методов
решения линейных систем.
Распространенным методом решения систем линейных уравнений является
метод Крамера, согласно которому оценки коэффициентов регрессии находятся
по формулам:
0
1
k
a0 ; .a1 ; ...; ak
(14)
где Δ – определитель коэффициентов при неизвестных системы (13);
j j 0,k – определители, которые формируются на основе определителя Δ
путем замены j-го столбца столбцом свободных членов.
13

14.

2. Скалярная форма построения уравнения регрессии.
Таким образом, развернутый вид данных определителей будет следующим:
n
i 1
n
f 02 ( xi )
f1( xi ) f0( xi )
i 1
n
n
f 0 ( xi ) f1( xi )
i 1
n
f0 ( xi ) f k ( xi )
i 1
i 1
n
f k ( xi ) f 0( xi )
i 1
n
f12 ( xi )
f1( xi ) f k ( xi )
i 1
n
f k ( xi ) f1( xi )
i 1
n
2
f
k ( xi )
i 1
14

15.

2. Скалярная форма построения уравнения регрессии.
n
n
i 1
i 1
n
yi f0 ( xi ) f1( xi ) f0( xi )
f k ( xi ) f 0( xi )
n
n
n
0 yi f1( xi )
i 1
n
yi fk ( xi )
i 1
i 1
n
f12 ( xi )
f1( xi ) f k ( xi )
i 1
i 1
f k ( xi ) f1( xi )
i 1
n
2
f
k ( xi )
i 1
15

16.

2. Скалярная форма построения уравнения регрессии.
n
i 1
n
f 02 ( xi )
n
1 f 0 ( xi ) f1( xi )
i 1
n
f0 ( xi ) f k ( xi )
i 1
n
yi f0( xi )
f k ( xi ) f 0( xi )
n
n
i 1
yi f1( xi )
i 1
n
yi f k ( xi )
i 1
i 1
f k ( xi ) f1( xi )
i 1
n
2
f
k ( xi )
i 1
16

17.

2. Скалярная форма построения уравнения регрессии.
n
i 1
n
f 02 ( xi )
f1( xi ) f0( xi )
i 1
n
n
k f 0 ( xi ) f1( xi )
i 1
i 1
n
n
i 1
i 1
n
yi f0( xi )
i 1
n
f12 ( xi )
f0 ( xi ) f k ( xi ) f1( xi ) f k ( xi )
yi f1( xi )
i 1
n
yi f k ( xi )
i 1
17

18.

2. Скалярная форма построения уравнения регрессии.
В результате будет получено уравнение регрессии с числовыми значения-ми
полученных коэффициентов регрессии:
y a0 f 0 (x) a1 f1 (x) ... ak f k (x)
(15)
Такова процедура реализации метода наименьших квадратов в скалярной
форме.
Пример 1. Построить в скалярной форме уравнение регрессии в виде
квадратичного алгебраического полинома
y a0 x 2 a1x a2
(П1)
18

19.

2. Скалярная форма построения уравнения регрессии.
Исходные данные заданы в виде следующего массива
x
-2
-1
0
2
y
1
-2
-1
14
Решение. Если полином (П1) представлять в общем виде, линейном
относительно параметров, то получается выражение
y a0 f 0 (x) a1 f1 (x) a2 f 2 (x)
(П2)
f 0 (x) x 2 f1 (x) = x f 2 (x) =1
(П3)
19

20.

2. Скалярная форма построения уравнения регрессии.
Поскольку объем массива данных n=4, система линейных уравнений (13)
принимает вид:
4
4
4
4 2
a0 f 0 (xi ) a1 f1 (xi )f 0 (xi ) a2 f 2 (xi )f 0 (xi ) yi f 0 (xi );
i 1
i 1
i 1
i 1
4
4
4
4
2
a0 f 0 (xi )f1 (xi ) a1 f1 (xi ) a2 f 2 (xi )f1 (xi ) yi f1 (xi ); (П4)
i 1
i 1
i 1
i 1
4
4
4
4
a0 f 0 (xi )f 2 (xi ) a1 f1 (xi )f 2 (xi ) a2 f 22 (xi ) yi f 2 (xi ).
i 1
i 1
i 1
i 1
20

21.

2. Скалярная форма построения уравнения регрессии.
Принимая во внимание (П3), система (П4) получает вид
4
4
4
4 4
3
2
2
a
x
a
x
a
x
y
x
i i;
1 i
2 i
0 i
i 1
i 1
i 1
i 1
4
4
4
4 3
2
a
x
a
x
0 i
1 i a2 xi yi xi ;
i 1
i 1
i 1
i 1
4
4
4 2
a0 xi a1 xi a2 4 yi .
i 1
i 1
i 1
(П5)
21

22.

2. Скалярная форма построения уравнения регрессии.
Для вычисления сомножителей при неизвестных составляется таблица
22

23.

2. Скалярная форма построения уравнения регрессии.
Система уравнений (П5) с числовыми значениями сомножителей:
33a0 a1 9a2 58;
a0 9a1 a2 28;
9a a 4a 12.
1
2
0
(П6)
Решение системы (П6) находится по формулам Крамера (14). Определители:
33 1 9
9 1
9
2
3 1 1
4 1
1 9 1 33( 1)
( 1)
9( 1)
1 4
9 4
9 1
9 1 4
33(36 1) +( 4 9) +9(1 81) =1155+5 720 440
23

24.

2. Скалярная форма построения уравнения регрессии.
Для справки
Вычисление определителя 3-го порядка разложением по строке (например, по первой строке) осуществляется на
основе формулы
a11 a12 a13
a21 a22 a23 a11 A11 a12 A12 a13 A13 ,
a31 a32 a33
где A11, A12, A13 – алгебраические дополнения элементов a11, a12, a13 соответственно.
Алгебраическое дополнение, например, элемента a12:
a21 a23
a21 a23
A12 = ( 1)1 2
( 1)3
(a21a33 a31a23 ) 1 4 9( 1) 5 .
a31 a33
a31 a33
Вычисление определителя 3-го порядка по правилу треугольников:
a11 a12 a13
a21 a22 a23 a11a22 a33 a21a32 a13 a31a12 a23 a31a22 a13 a11a32 a23 a21a12 a33 .
a31 a32 a33
24

25.

2. Скалярная форма построения уравнения регрессии.
Остальные определители:
58 1 9
33 58 9
33 1 58
0 28 9 1 930 1 1 28 1 1426 2 1 9 28 416
9 12 4
12 1 4
9 1 12
Оценки коэффициентов регрессии:
a0
930
=2,11;
440
a1
1426
3,24;
440
В итоге получено уравнение регрессии:
a2
416
0,95
440
y 2,11x 2 3,24 x 0,95
25

26.

3. Матричная форма построения уравнения регрессии.
Система уравнений (13) эквивалентна следующему матричному уравнению:
(F[kт 1;n ] F[n;k 1] )A k 1 F[kт 1;n ]Y n
f 0 ( x1 )
F k 1,n f 0 ( xi )
f 0 ( xn )
f1 ( x1 )
f1 ( xi )
f1 ( xn )
f k ( x1 )
f k ( xi )
f k ( xn )
(16)
A k 1 a0 , a1 ,...,ak 1
т
Y n y1 , y2 ,..., yn
т
26

27.

3. Матричная форма построения уравнения регрессии.
Для того, чтобы выразить неизвестный вектор, обе части матричного уравнения
т
1
(16) необходимо умножить слева на квадратную матрицу (F F )[k 1]
(F т F ) 1 (F т F )A (F т F ) 1F тY
Далее учитывается, что
(F т F ) 1 (F т F ) E; EA A
Где E = E[k+1] – единичная матрица порядка k+1.
Окончательное выражение для вычисления вектора оценок коэффициентов
регрессии:
A k 1 (F[kт 1;n ] F[n;k 1] ) 1F[kт 1;n ]Y n
(17)
27

28.

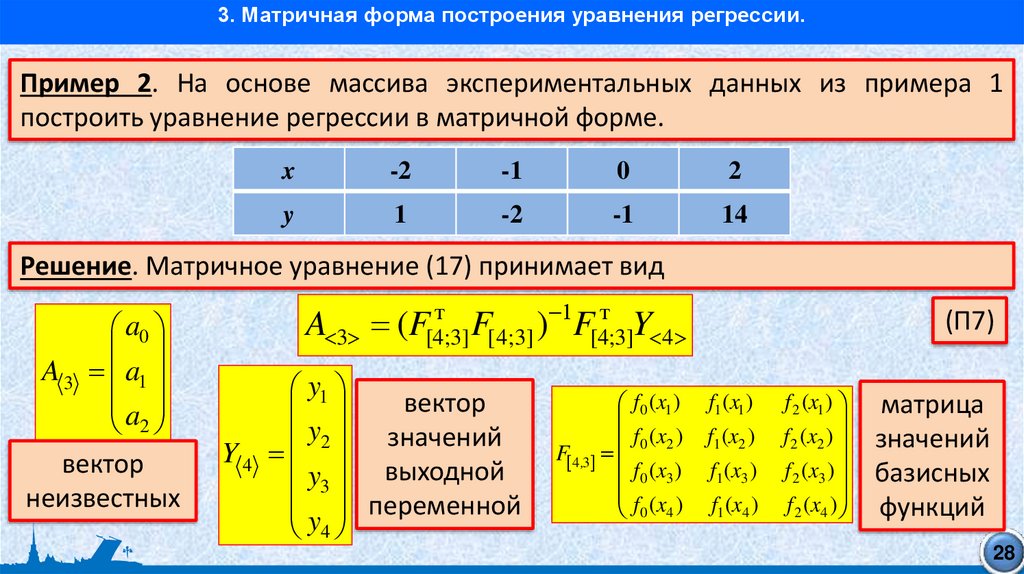
3. Матричная форма построения уравнения регрессии.
Пример 2. На основе массива экспериментальных данных из примера 1
построить уравнение регрессии в матричной форме.
x
-2
-1
0
2
y
1
-2
-1
14
Решение. Матричное уравнение (17) принимает вид
a0
A 3 a1
a
2
вектор
неизвестных
т
т
A 3 (F[4;3]
F[4;3] ) 1F[4;3]
Y 4
y1
вектор
y2 значений
Y4
y3 выходной
переменной
y4
f 0 (x1 )
f 0 (x2 )
F 4 ,3
f 0 (x3 )
f 0 (x4 )
(П7)
f1 (x1 )
f1 (x2 )
f1 (x3 )
f1 (x4 )
f 2 (x1 )
f 2 (x2 )
f 2 (x3 )
f 2 (x4 )
матрица
значений
базисных
функций
28

29.

3. Матричная форма построения уравнения регрессии.
поскольку уравнение строится в виде квадратичного алгебраического
полинома, то
f 0 (x) x 2 f1 (x) = x f 2 (x) =1
С учетом приведенных обозначений
x12
2
x2
F 4 ,3 2
x3
x2
4
x1
x2
x3
x4
1 4
1 1
= 0
1
1 4
2 1
1 1
.
0 1
2 1
29

30.

3. Матричная форма построения уравнения регрессии.
Находим произведение транспонированной матрицы Fт на исходную:
4 1
т
F[4;3]
F[4;3] 2 1
1
1
4
0 4
1
0 2
0
1 1
4
2 1
33 1 9
1 1
1
9 1
0 1
9 1 4
2 1
Далее требуется найти обратную матрицу (F т F ) 1
30

31.

3. Матричная форма построения уравнения регрессии.
Для справки
Пусть имеется матрица 3-го порядка
a11
A a21
a
31
a12
a22
a32
a13
a23 .
a33
Тогда обратная матрица находится по формуле:
A11 A21 A31
1
A 1 A12 A22 A32 ,
A
A13 A23 A33
где |A| - определитель матрицы А, Aij – алгебраические дополнения элементов aij.
31

32.

3. Матричная форма построения уравнения регрессии.
Алгебраические дополнения элементов матрицы Fт F
9 1
3 1 1
5
A11 ( 1)
35 A12 ( 1)
9 4
1 4
1 9
A13 ( 1)
80
9 1
1 9
A21 ( 1)
5
1 4
33 1
A23 ( 1)
24
9 1
2
3
A31 ( 1)
33 9
A22 ( 1)
51
9 4
4
4
5
1
9
9
6 33
5 33
296
80 A32 ( 1)
24 A33 ( 1)
1 9
9 1
1 1
4 1
|A| = 440
32

33.

3. Матричная форма построения уравнения регрессии.
Обратная матрица:
35
1
(F т F ) 1
5
440
80
5 80
51
24
24 296
Произведение транспонированной матрицы F на вектор Y:
4 1
F тY 2 1
1
1
1
0 4 58
2
0 2
28
1
1 1 12
14
33

34.

3. Матричная форма построения уравнения регрессии.
В соответствии с матричным уравнением (П7):
35 5 80 58
1
28
A (F т F ) 1F тY
5
51
24
440
80 24 296 12
35 58 5 28 80 12
930 2,11
1
1
3,24
5
58
51
28
24
12
1426
440
440
416 0,95
80 58 24 28 296 12
Оценки коэффициентов регрессии:
Получено уравнение регрессии, как
и при реализации скалярной формы:
a0 2,11; a1 3,24;
a2 0,95
y 2,11x 2 3,24 x 0,95
34

35.

4. Проверка адекватности уравнения регрессии по критерию Фишера.
Этапы проверки адекватности уравнения регрессии
1. Выдвигается гипотеза о том, что построенное уравнение адекватно
экспериментальным данным и формируется показатель согласованности
данной гипотезы:
2
ˆ
F
12
В числителе выражения (18):
y
n
1
yi
n i 1
среднее
арифметическое
значение выходной
переменной
n
(yi y )2
2 i 1
n 1
(18)
оценка дисперсии
выходной переменной
n-1 - число степеней свободы, при которых
находится оценка дисперсии выходной переменной
35

36.

4. Проверка адекватности уравнения регрессии по критерию Фишера.
В знаменателе выражения (18):
n
(yi yi )2
12 i 1
n k 1
yi
оценка остаточной
дисперсии
теоретические значения выходной переменной
n-k-1=n-(k+1) - число степеней свободы, при которых находится оценка
остаточной дисперсии
(k+1) - количество коэффициентов в уравнении регрессии
k - степень алгебраического полинома, в виде которого строится уравнение
регрессии
36

37.

4. Проверка адекватности уравнения регрессии по критерию Фишера.
2. Вычисляются оценки дисперсий σ2 и 12 , находится наблюдаемое значение F
показателя (18).
3. Находится критическое значение F ( ; n 1; n k 1) показателя (18) по
таблицам критических точек распределения Фишера (приложение 5), где α –
уровень значимости проверяемой гипотезы (задается исследователем).
4. Проверяется условие
F F( ; n 1; n k 1)
(19)
Если условие (19) выполняется, гипотеза об адекватности уравнения
экспериментальным данным принимается, в противном случае – отвергается.
37

38.

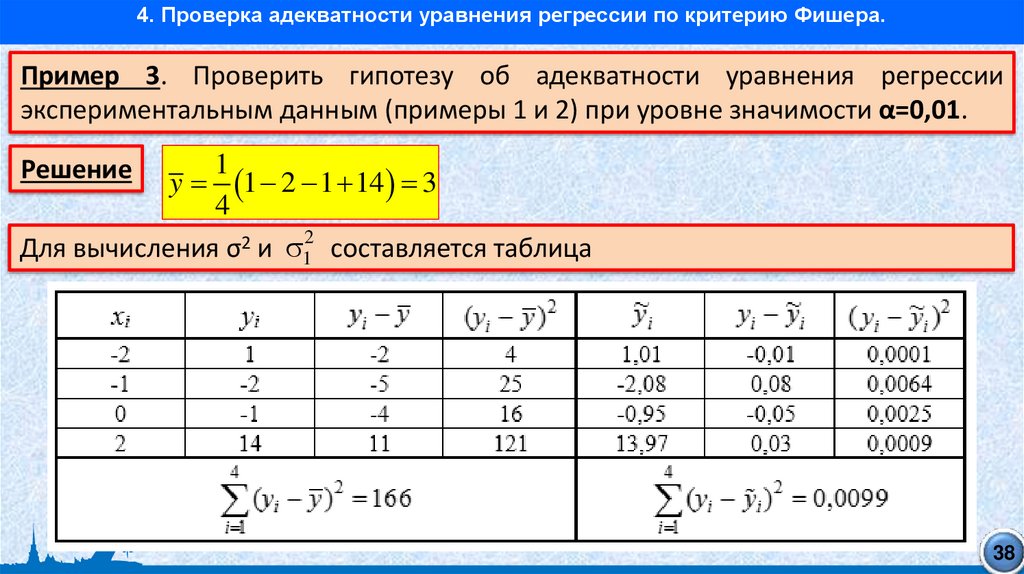
4. Проверка адекватности уравнения регрессии по критерию Фишера.
Пример 3. Проверить гипотезу об адекватности уравнения регрессии
экспериментальным данным (примеры 1 и 2) при уровне значимости α=0,01.
1
1 2 1 14 3
4
Для вычисления σ2 и 12 составляется таблица
Решение
y
38

39.

4. Проверка адекватности уравнения регрессии по критерию Фишера.
Теоретические значения выходной переменной, например:
y1 2,11( 2) 2 3,24( 2) 0,95 1,01
Оценка дисперсии выходной переменной:
4
2
(
y
y
)
i
2 i 1
4 1
166
55,3
3
Оценка остаточной дисперсии:
4
(yi yi )2
12 i 1
4 2 1
0,0099
0,0099
1
39

40.

4. Проверка адекватности уравнения регрессии по критерию Фишера.
Наблюдаемое значение показателя согласованности гипотезы об адекватности
уравнения регрессии экспериментальным данным:
F
55,3
5586
0,0099
Критическое значение показателя согласованности гипотезы: F(0,01; 3; 1) = 5403
Поскольку
F F(0,01; 3; 1),
то гипотеза об адекватности уравнения регрессии экспериментальным данным
принимается.
40

41.

5. Проверка значимости коэффициентов регрессии по критерию Стъюдента.
Этапы проверки значимости коэффициентов регрессии по критерию Стъюдента
1. Выдвигается гипотеза о значимости коэффициента регрессии aj
формируется показатель согласованности данной гипотезы:
t̂ j
j 0, k
и
|aj |
(20)
aj
|aj |
модуль величины aj
a j
оценка среднего квадратического отклонения коэффициента aj
2. Формируется корреляционная матрица для вычисления a j :
K A[k 1] 12 (F[kт 1; n ] F[n; k 1] ) 1
(21)
41

42.

5. Проверка значимости коэффициентов регрессии по критерию Стъюдента.
На главной диагонали матрицы (21) будут дисперсии оценок коэффициентов
регрессии:
diagK A a20 , a21 ,..., a2k
Тогда
(22)
a j = a2 j
3. Вычисляются наблюдаемые значения показателя (20).
4. Находится критическое значение t ( ; n k 1) показателя (20) по таблицам
критических точек распределения Стъюдента (приложение 6), где α – уровень
значимости проверяемой гипотезы (задается исследователем).
42

43.

5. Проверка значимости коэффициентов регрессии по критерию Стъюдента.
5. Проверяется условие
t j t ( ; n k 1), j 0, k
(23)
Если условие (23) выполняется, гипотеза о значимости коэффициента регрессии
aj принимается, в противном случае – отвергается.
Коэффициенты регрессии, для которых не выполняется условие (23),
принимаются равными нулю. При этом соответствующие слагаемые
исключаются из уравнения регрессии. Уравнение с новой структурой
проверяется на адекватность экспериментальным данным по критерию
Фишера. Если гипотеза об адекватности уравнения с новой структурой
отвергается, производится возврат к первоначальной структуре уравнения.
Иначе, проверка по критерию Фишера имеет приоритет над проверкой по
критерию Стъюдента.
43

44.

5. Проверка значимости коэффициентов регрессии по критерию Стъюдента.
Пример 4. Проверить значимость коэффициентов регрессии в уравнении
(примеры 1 и 2) при уровне значимости α=0,01 .
Решение. Элементы главной диагонали корреляционной матрицы (22):
diag 12 (F т F ) 1 2a0 , 2a1 , 2a2
35
51
296
0,0099
, 0,0099
, 0,0099
440
440
440
0,00079, 0,00115, 0,00666
Таким образом
a0 0,00079 0,028 a 0,00115 0,034
1
a2 0,00666 0,082
44

45.

5. Проверка значимости коэффициентов регрессии по критерию Стъюдента.
Наблюдаемые значения показателя согласованности (20):
t0
2,11
75,4
0,028
t1
3,24
92,3
0,034
0,95
0,95
t2
11,6
0,082 0,082
Критическое значение показателя согласованности гипотезы о значимости
коэффициентов регрессии:
t (0,01; 1) = 63,7
Поскольку
t0 t (0,01; 1) t1 t (0,01; 1) t2 t (0,01; 1)
то гипотезы о значимости коэффициентов a0 и a1 принимаются, а гипотеза о
значимости коэффициента a2 отвергается.
45

46.

5. Проверка значимости коэффициентов регрессии по критерию Стъюдента.
Уравнение регрессии с новой структурой
y 2,11x 2 3,24 x
Данное уравнение проверяется на адекватность экспериментальным данным
также, как в примере 3. В результате проверки гипотеза об адекватности
уравнения с новой структурой отвергается.
Окончательный вид уравнения регрессии
y 2,11x 2 3,24 x 0,95
46