Матрицы, действия над матрицами. Определители 2-го и 3-го порядка

1. Матрицы, действия над матрицами. Определители 2-го и 3-го порядка.

Миноры и
алгебраические дополнения

2. Матрица

Матрица – множество чисел, образующих
прямоугольную таблицу, которая
содержит m-строк и n-столбцов.
aij, i – номер строки, j – номер столбца.

3.

Две матрицы называются равными, если они
имеют одинаковые размеры и их
соответствующие элементы равны.
Если количество столбцов матрицы совпадают
с количеством строк, то матрица называется
квадратной.
1.
2.
3.
Элементы матрицы, стоящие на диагонали,
идущие из верхнего левого угла называют
главной диагональю, другую диагональ
называют побочной.
Если количество строк m матрицы не равно
количеству столбцов n, то матрица называется
прямоугольной.

4.

Если все элементы квадратной матрицы, кроме
элементов главной диагонали, равны нулю, то
матрица называется диагональной.
Если все числа главной диагонали равны
единице, то матрица называется единичной.

5.

Если в прямоугольной матрице m=1, то
получается матрица-строка.
x (1;5;7)
Если n=1, то получается матрица-столбец.
Матрицы-строки и матрицы-столбцы
называются векторами.

6. Сложение матриц

Матрицы можно складывать только одинакового
размера.
Суммой двух матриц А и В называется матрица С,
элементы которой равны сумме соответствующих
элементов матриц А и В.
Сложение матриц подчиняется
переместительному и сочетательному
законам:
А+В=В+А
(А+В)+С=А+(В+С).
Нулевая матрица при сложении матриц выполняет
роль обычного нуля при сложении чисел: А+0=А.

7. Вычитание матриц

Разностью матриц А и В называется матрица
С, элементы которой равны разности
соответствующих элементов матриц А и В.
ЗАДАНИЯ:
1) 2
2)
5 6 7
0 3 8
3) 2 3 5 1 0 4
2 5 6 7
7 0 3 8
2 3 5 1 0 4
0 1 3 3 5 6
7
0
4)
1 3 3 5 6

8. Умножение матрицы на число

При умножении матрицы A на число a все
числа, составляющие матрицу A, умножаются
на число a.
ЗАДАНИЯ:
1) вычислить 5А-2В,
2) вычислить 5А+2В
если
2 3
A
1 0
1
3
B
1 2

9. Умножение матриц

Рассмотрим на примере:
Правила умножения матриц:
Умножение матрицы А на матрицу В имеет
смысл в том случае, когда число столбцов
матрицы А совпадает с числом строк в
матрице В.
В результате умножения двух прямоугольных
матриц получается матрица, содержащая
столько строк, сколько строк было в первой
матрице и столько столбцов, сколько столбцов
было во второй матрице.

10. Умножение матриц

ЗАДАНИЯ:
1)
2 5 6 7
7 0 3 8
2)
6 7 2 5
3 8 7 0
3)
1 3
2 3 5
0 5
0 1 3 4 6
4)
1 3
2 3 5
0 5
4 6 0 1 3
A B B A

11. Транспонирование матрицы

Транспонированная матрица – матрица AТ,
полученная из исходной матрицы A заменой
строк на столбцы.
Например,

12. Свойства матриц:

A + (B + C) = (A + B) + C
A + B = B + A
A(BC) = (AB) C
A (B + C) = AB + AC
(B + C) A = BA + CA
(AT) T = A
(A + B)T = AT + BT
(A · B) T = BT · AT

13. Определитель 2-го порядка

Определителем 2-го порядка называют
число, равное
Пример:
a11 a12
d
a11a22 a12a21
a21 a22

14. Вычисление определителей 2-го порядка

1)
2 1
3 2
2)
2 5
1 2
3)
21
32
a11 a12
d
a11a22 a12a21
a21 a22

15. Определитель 3-го порядка

Определителем 3-го порядка называют
число, равное
a11 a12 a13
d a21 a22 a23 a11a22a33 a21a32a13 a12a23a31 a13a22a31 a23a32a11 a21a12a33
a31 a32 a33
Пример:

16. Вычисление определителей 3-го порядка

1)
Вычисление
определителей 3-го порядка
2)
Свойства определителя:
1) Если матрицу транспонировать, то
определитель не изменится.
Проверьте это свойство на предыдущем
примере.

17. Свойства определителя:

2) Если все элементы строки (столбца)
умножить на одно и тоже число, то
определитель умножится на это число.
Проверьте это свойство
A 2A
3) Если поменять местами две строки
(столбца), то определитель поменяет
знак.
Проверьте это свойство на
предыдущем примере

18. Свойства определителя:

4) Если хотя бы одна строка (столбец)
нулевая, то определитель равен нулю.
Проверьте это свойство
5) Если две строки (столбца) равны, то
определитель равен нулю.
Проверьте это свойство

19. Свойства определителя:

6) Если одна строка (столбец) является
линейной комбинацией других строк
(столбцов), то определитель равен нулю.
7) Если каждый элемент некоторой строки
(столбца) определителя представлен в виде
суммы двух слагаемых, то определитель равен
сумме двух определителей, у которых все
строки (столбцы), кроме данной, прежние, а в
данной строке (столбце) в первом
определителе стоят первые, а во втором вторые слагаемые.
8) Определитель не меняется если к одной из
его строк (столбцов) добавить линейную
комбинацию его других строк (столбцов)

20. МИНОР

Минором Mij к элементу aij определителя n-го
порядка называется определитель (n - 1)-го
порядка, полученный из исходного
определителя вычеркиванием i-той строки и jтого столбца.
ПРИМЕР
Найти и вычислить М23 к элементу а23
определителя
Решение:

21. Вычисление миноров

Задания:
1) Найти и вычислить М12 к элементу а12
определителя
1 3 2
9 0 5
4 3 7
M12 83
2) Найти и вычислить М32 к элементу а32
определителя
1 0 3 9
2 7 11 5
9 4 25 84
4 12 558
M 32 579

22. Вычисление миноров

Задания:
3) Найти и вычислить все миноры
определителЯ

23. Алгебраическое дополнение

Алгебраическим дополнением Aij к
элементу aij определителя n-го порядка
называется число: Aij = (-1)i + j · Mij
ПРИМЕР
Найти и вычислить А23 к элементу
а23 определителя
Решение:

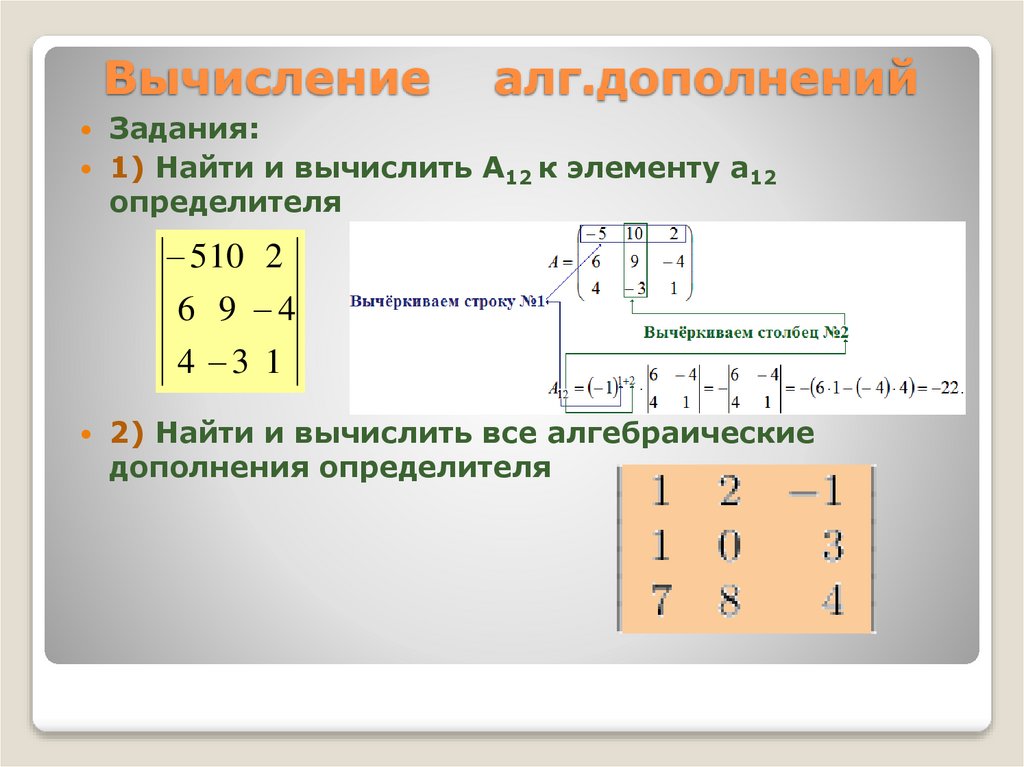
24. Вычисление алг.дополнений

Задания:
1) Найти и вычислить А12 к элементу а12
определителя
510 2
6 9 4
4 3 1
2) Найти и вычислить все алгебраические
дополнения определителя

25. Домашнее задание:

• 1) вычислить 2А, 3В,
2А-3В, А·В
•2) вычислить
A и B
3 2
A
1
0
7 1
B
1 1
•3) найти и вычислить все миноры и все
алгебраические дополнения
определителя
1 2 1
7 1 3
2 3 0
Успехов при решении!!!