Похожие презентации:
Магнитное поле в центре витка с током
1.
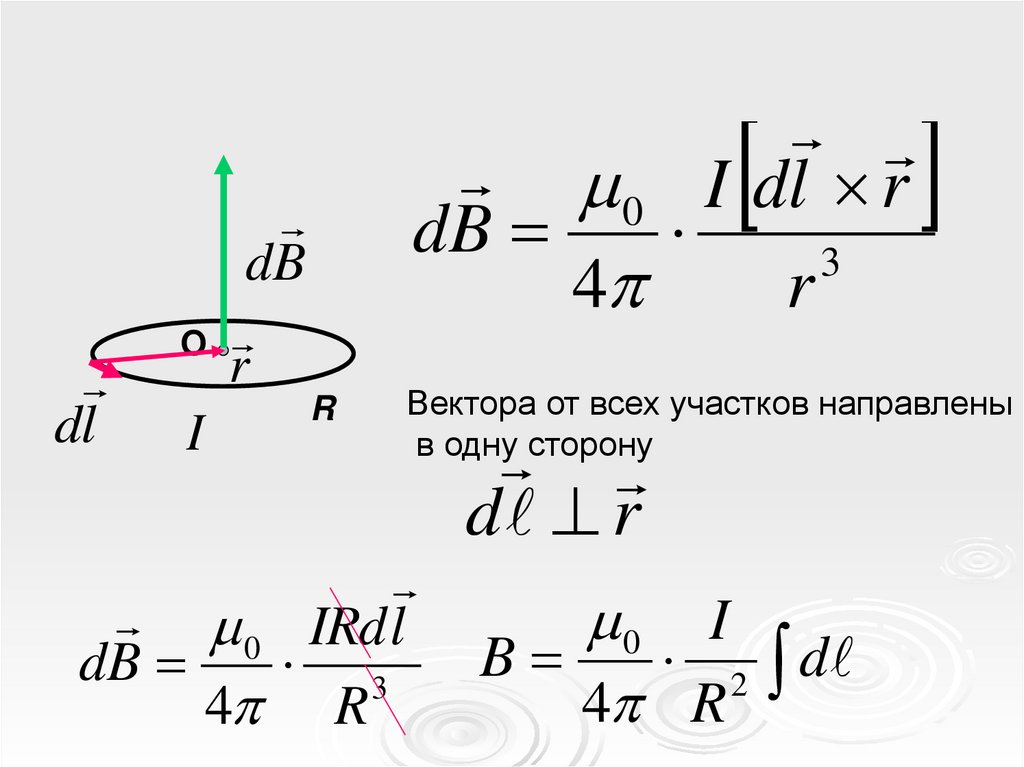
Магнитное поле вцентре витка с током
2.
dldB
O
r
R
I
0 I dl r
dB
3
4
r
Вектора от всех участков направлены
в одну сторону
0 IRd l
dB
3
4 R
d r
0 I
B
2 d
4 R
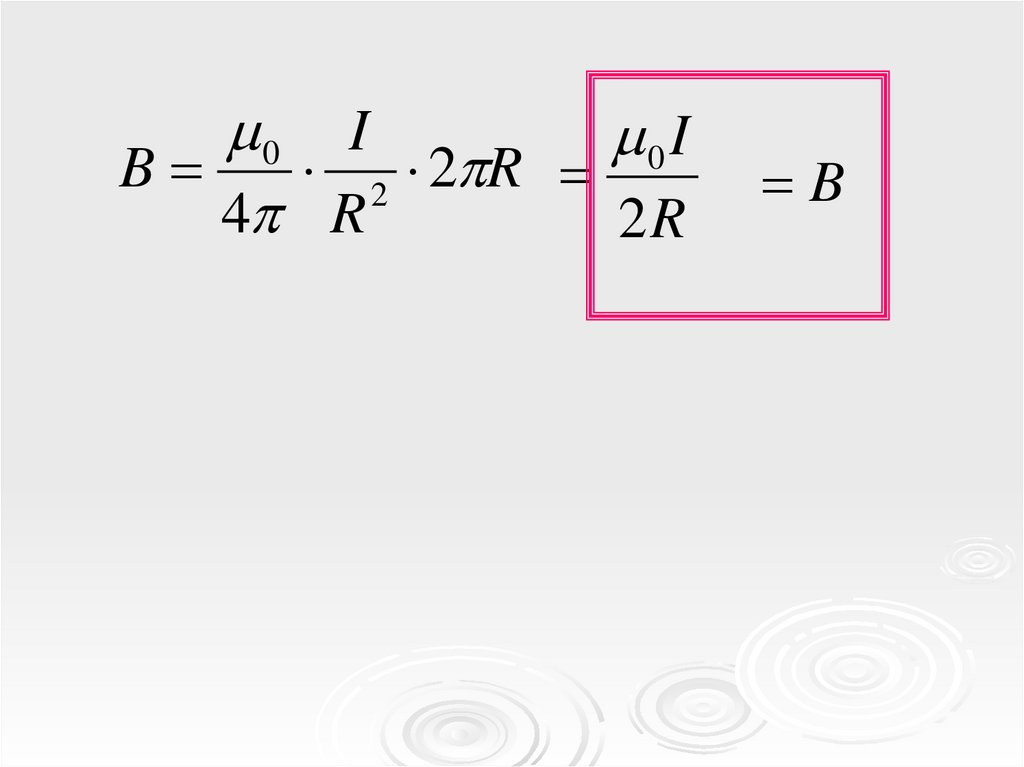
3.
0 I0 I
B
2 2 R
4 R
2R
B
4.
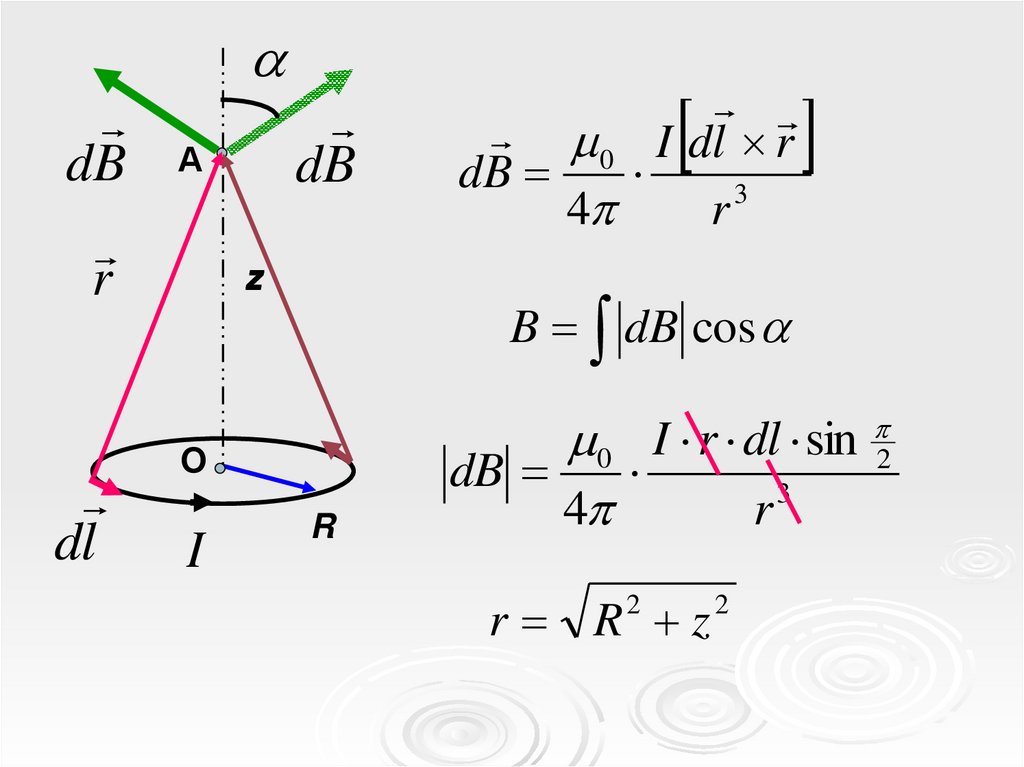
МАГНИТНОЕ ПОЛЕ НАОСИ ВИТКА С ТОКОМ
5.
dBr
dl
dB
А
z
B dB cos
O
I
0 I dl r
dB
3
4
r
R
0 I r dl sin 2
dB
3
4
r
r R z
2
2
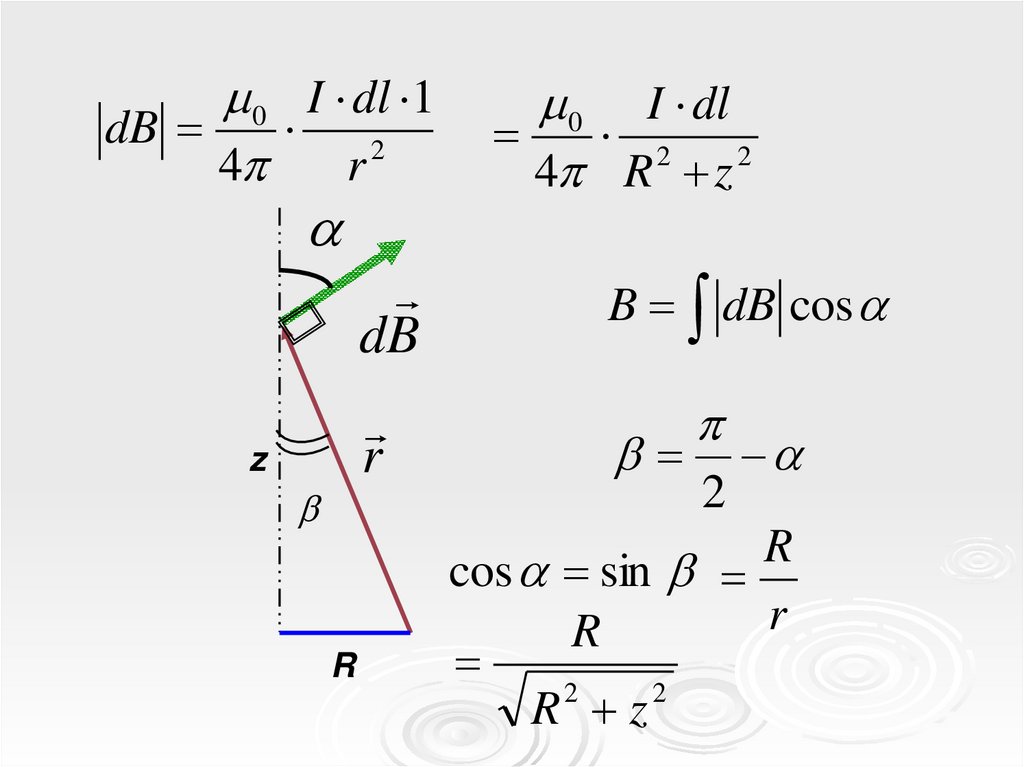
6.
0 I dl 1dB
4
r2
dB
r
z
R
0 I dl
2 2
4 R z
B dB cos
2
R
cos sin
r
R
2
2
R z
7.
0 I R dlB
3
2
2
4 R z 2
0
I R
dl
3
4 R 2 z 2 2
dl 2 R
0 I R 2 R
0
I R2
B
B
3
3
4 R 2 z 2 2
2 R 2 z 2 2
8.
Закон Ампера9.
На проводник с током, помещенный вмагнитное поле действует сила,
называемая силой Ампера.
I
B
dℓ
dF
B
dF I dl B
dF I dl B sin
α – угол между векторами dl и B
10.
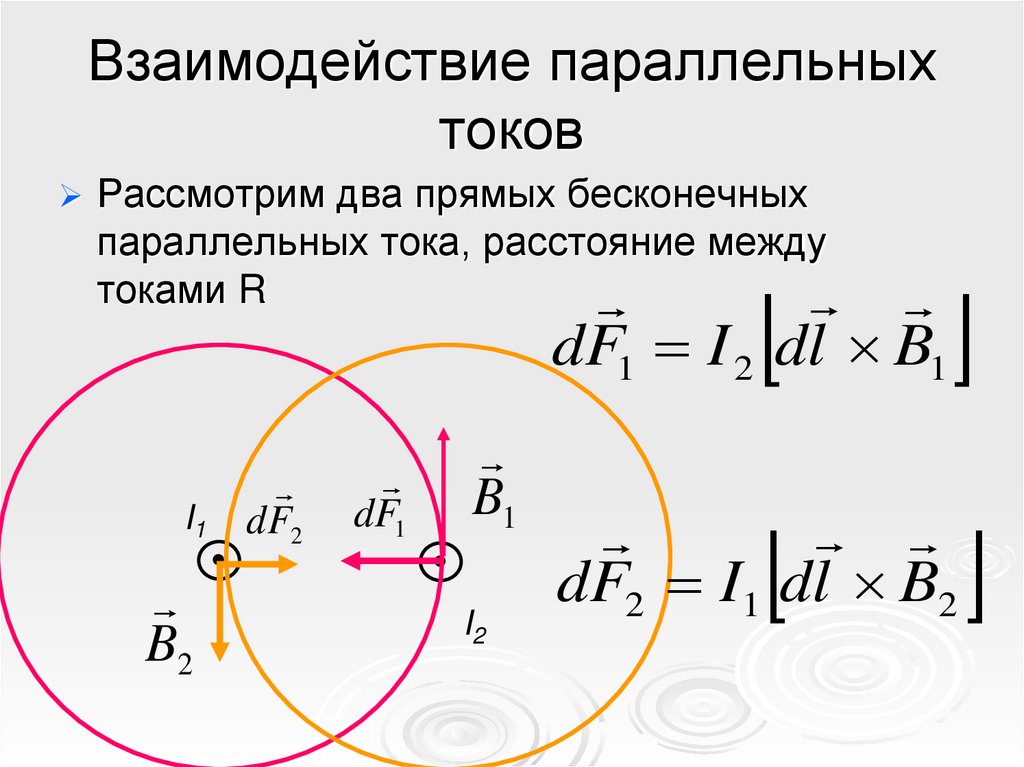
Взаимодействие параллельныхтоков
Рассмотрим два прямых бесконечных
параллельных тока, расстояние между
токами R
I1
B2
dF2
dF1
B1
I2
dF1 I 2 dl B1
dF2 I1 dl B2
11.
dF1 I 2 B1dldF2 I1B2 dl
0 I1
B1
2 R
0 I 2
B2
2 R
0 I 2
0 I1
dl
dF1 I 2
dl dF2 I1
2 R
2 R
0 I1 I 2
dF1 dF2
dl
2 R
12.
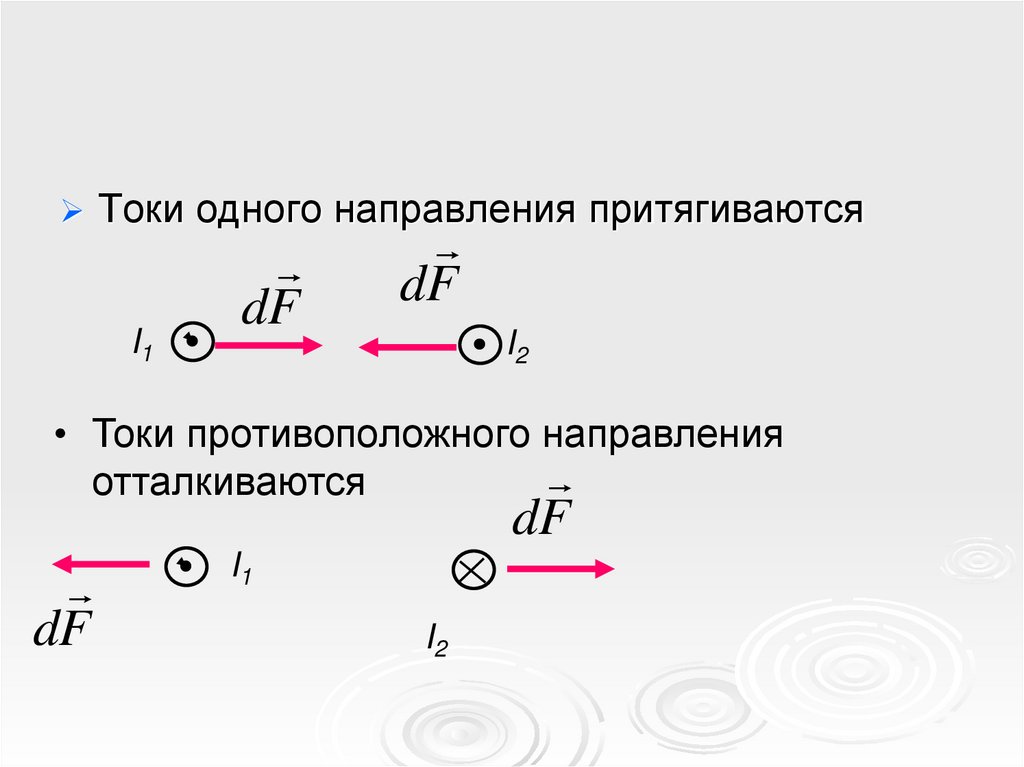
Токи одного направления притягиваютсяI1
dF
dF
I2
• Токи противоположного направления
отталкиваются
dF
dF
I1
I2
13.
Основные законымагнитного поля
14.
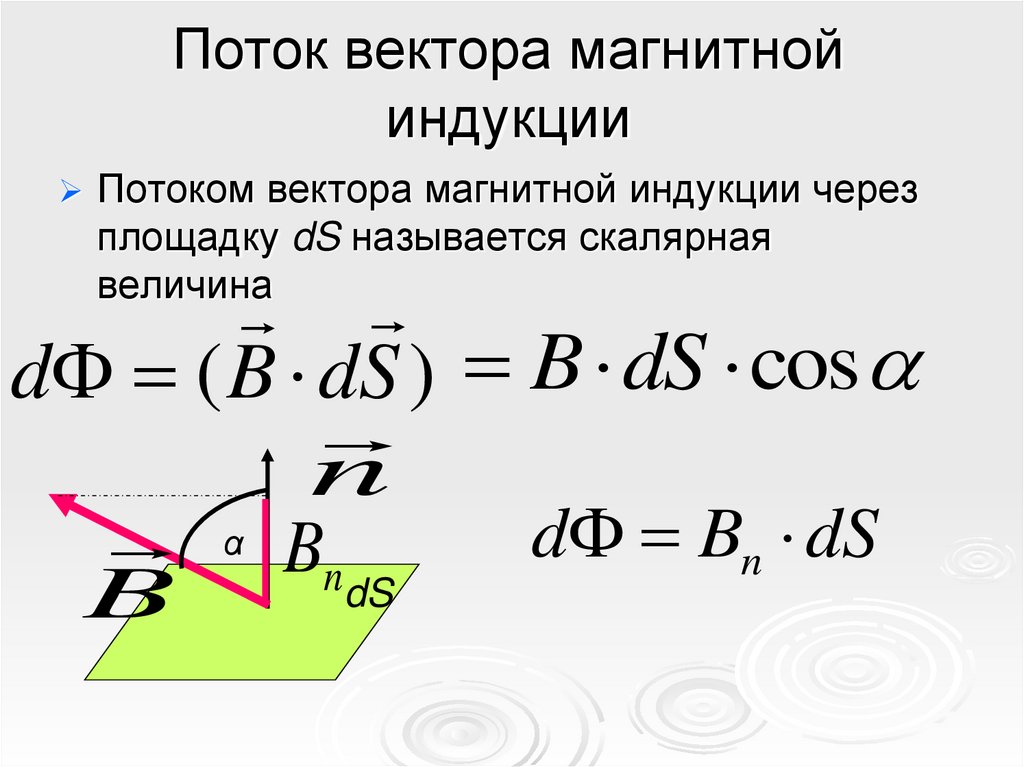
Поток вектора магнитнойиндукции
Потоком вектора магнитной индукции через
площадку dS называется скалярная
величина
d ( B dS ) B dS cos
n
α Bn
dS
B
d Bn dS
15.
Поток может быть как положительным, так иотрицательным, это зависит от взаимного
расположения площадки и вектора магнитной
индукции.
cos 0,
d 0
cos 0,
d 0
16.
магнитной индукциичерез произвольную ( B dS )
Поток вектора
поверхность S
S
Поток вектора
магнитной индукции
измеряется в
веберах (Вб)
1 Вб = 1 Тлּ1м2
17.
Теорема Гаусса для векторамагнитной индукции
Поток вектора магнитной индукции
через произвольную замкнутую
поверхность равен нулю.
(
B
d
S
)
0
S
18.
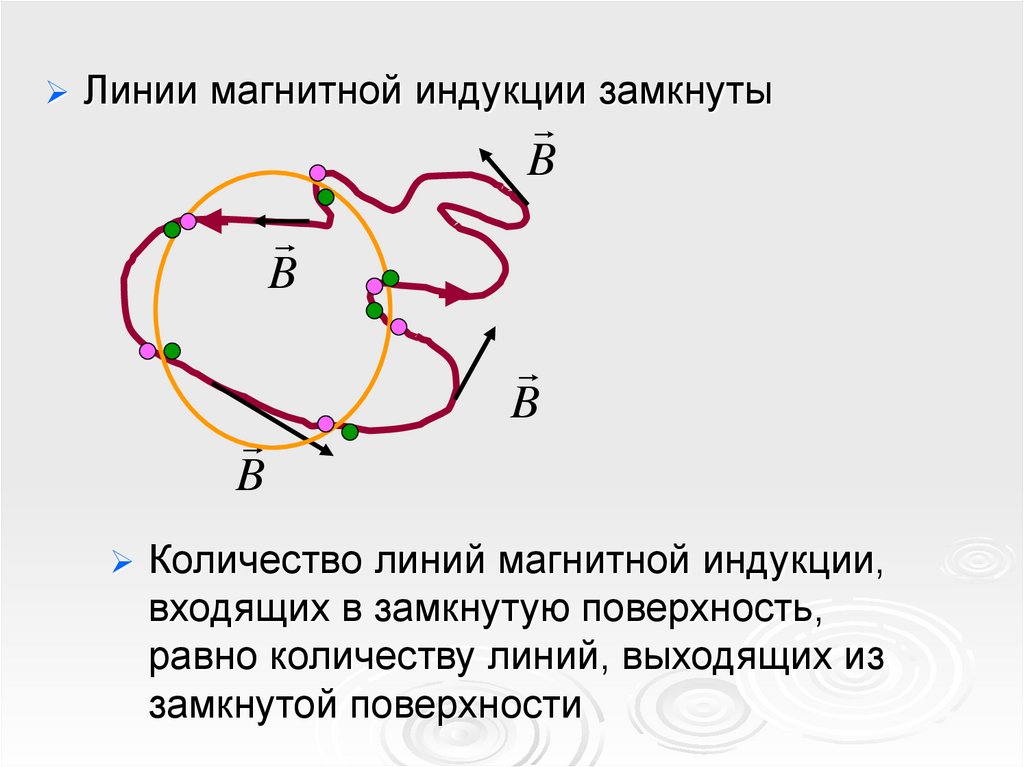
Линии магнитной индукции замкнутыB
B
B
B
Количество линий магнитной индукции,
входящих в замкнутую поверхность,
равно количеству линий, выходящих из
замкнутой поверхности
19.
Следствие теоремы ГауссаПоток вектора магнитной индукции
через поверхность, ограниченную
замкнутым контуром, не зависит от
формы поверхности
В природе нет магнитных зарядов !!!
20.
Теорема о циркуляции векторамагнитной индукции
Циркуляция вектора
магнитной индукции
по произвольному
контуру L равна
произведению μ0 на
алгебраическую
сумму токов,
охватываемых
контуром.
N
( B dl ) 0 I k
L
k 1
21.
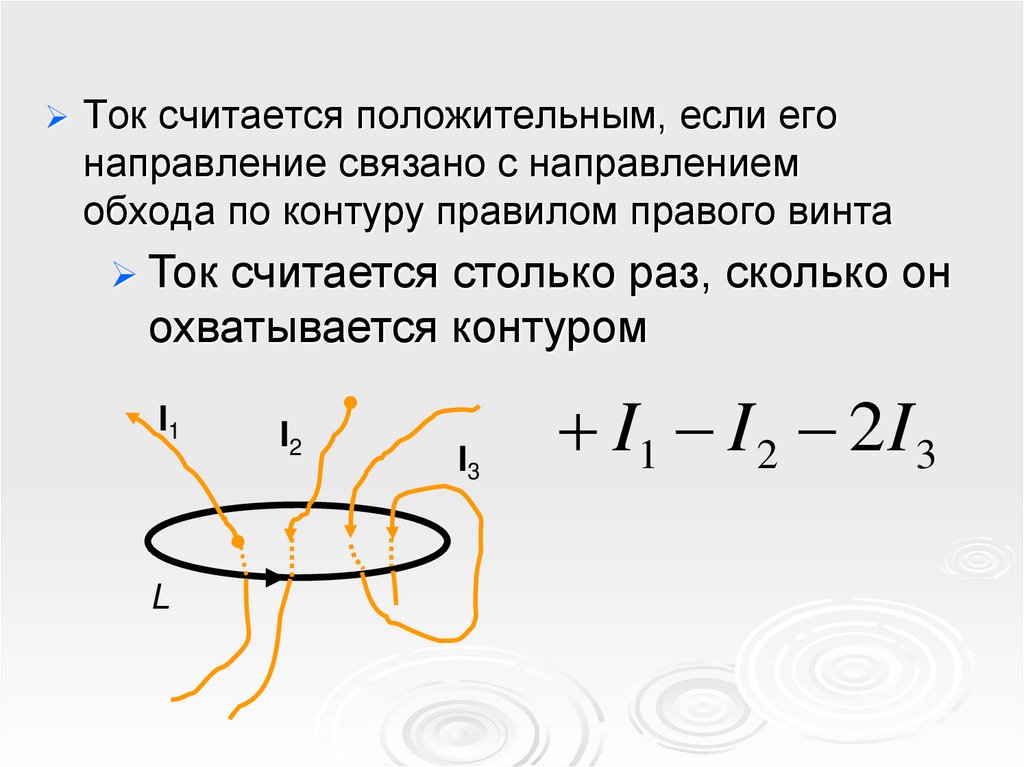
Ток считается положительным, если егонаправление связано с направлением
обхода по контуру правилом правого винта
Ток считается столько раз, сколько он
охватывается контуром
I1
L
I2
I3
I1 I 2 2I 3
22.
Если токI ( j dS )
распределен по
объему, то его
можно представить
в виде
S
j – плотность тока
(
B
d
l
)
(
j
d
S
)
0
L
S
Интеграл берется по произвольной
поверхности S, натянутой на контур L.
23.
Циркуляция вектора магнитнойиндукции отлична от нуля, такое поле
называется
вихревым
24.
Применение теоремы оциркуляции вектора магнитной
индукции
25.
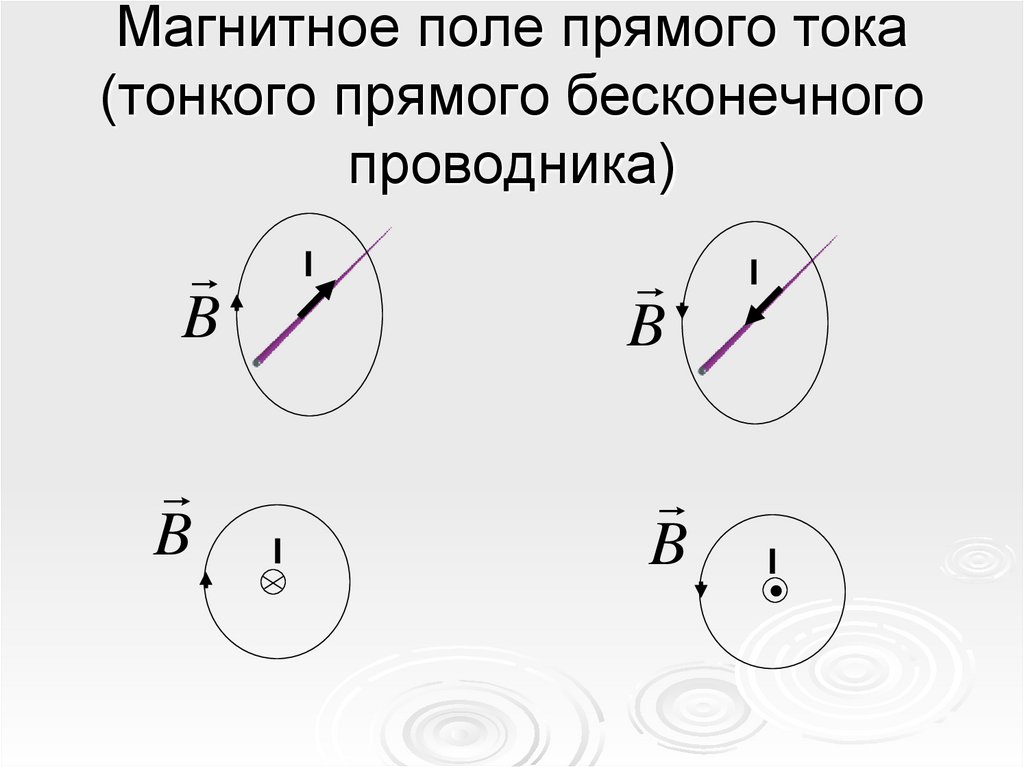
Магнитное поле прямого тока(тонкого прямого бесконечного
проводника)
B
B
I
I
B
B
I
I
26.
dlr
I
B
L
N
( B dl ) 0 I k
k 1
L
B dl 0 I
L
B 2 r 0 I
0 I
B
2 r
27.
Магнитное поле соленоидаСоленоид-это цилиндр , на который намотана
проволока. Длина соленоида L, количество
витков N.
I
I
B
Считаем, что
магнитное поле
однородно и
сосредоточено внутри
соленоида
28.
BB
A
ℓ
D
ABCD
N
( B dl ) 0 I k
k 1
C ABCD
( B dl ) ( B dl ) ( B dl ) ( B dl ) ( B dl )
AB
BC
( B dl ) B dl B dl B l
AB
AB
AB
CD
(
B
d
l
)
B
dl
cos
2 0 ( B dl ) 0
BC
BC
( B dl ) 0 dl 0
CD
CD
DA
DA
29.
Nn
L
Число витков на единицу длины
N
N
Ik I l I n l
L
k 1
N
B l 0 I l
L
N
B 0 I
L
30.
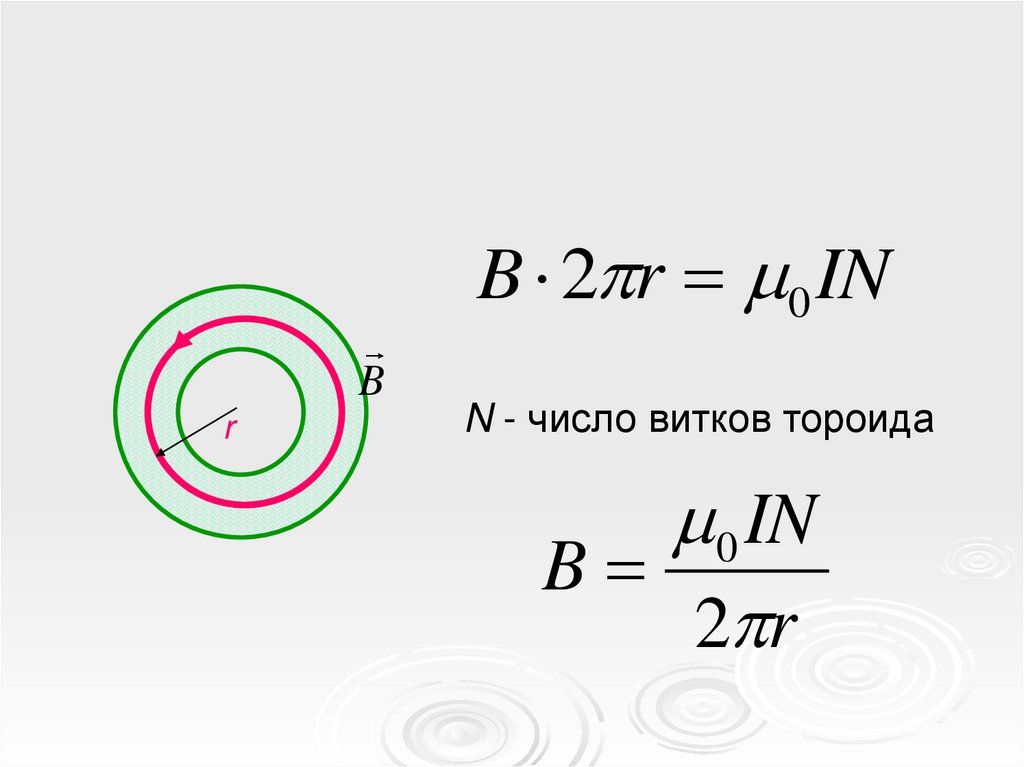
Магнитное поле тороидаТороид – это бублик, на который
намотан провод
Магнитное поле сосредоточено внутри
тороида, снаружи поле отсутствует
Линии магнитной индукции –
окружности с центром на оси тороида
31.
Br
B 2 r 0 IN
N - число витков тороида
0 IN
B
2 r





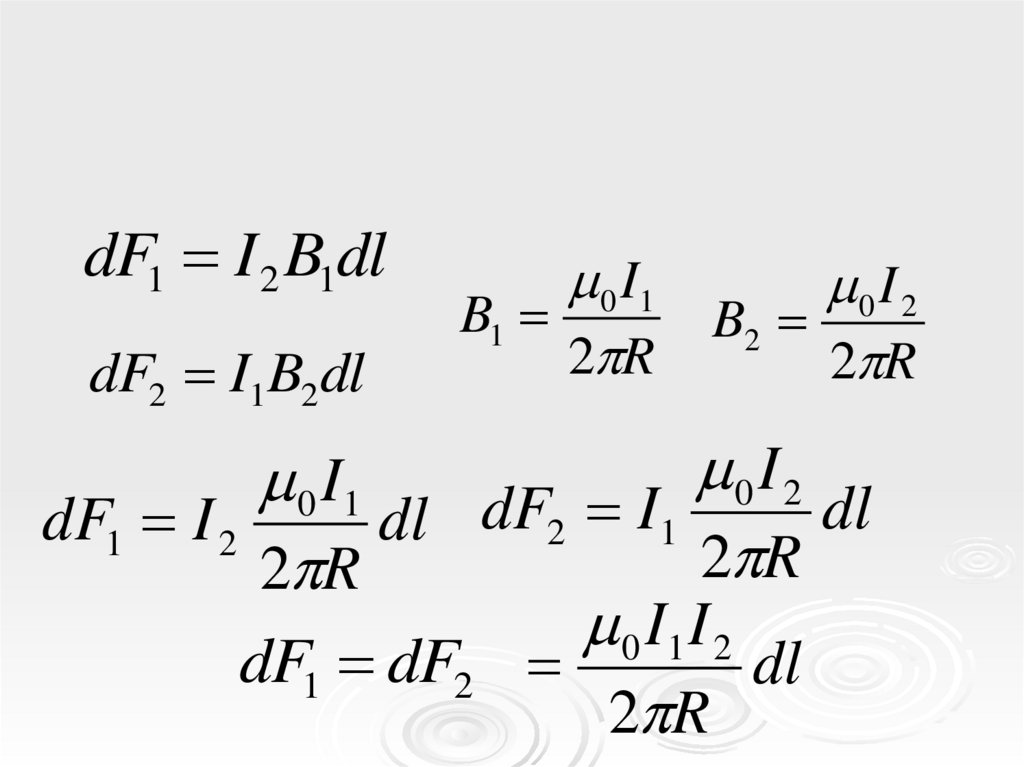














 Физика
Физика








