Похожие презентации:
Понятие логарифма. Определение логарифма
1.
ПОНЯТИЕЛОГАРИФМА
2.
Определение логарифмаЛогарифмом числа b по основанию а
называется показатель степени,
в которую нужно возвести а, чтобы
получить b.
log a b c ,
a 0,
a b,
a 1,
c
b 0
3.
Виды логарифмовОбыкновенные
Натуральные
Десятичные
4.
Обыкновенные логарифмы:log 2 7
Читается:
«логарифм 7 по
основанию 2»
log a 1 0
log a a 1
a
loga x
x
5.
Натуральные логарифмы:log e 5 ln 5
Читается:
«натуральный
логарифм 5»
ln 1 0
ln e 1
e
ln x
x
6.
Число еЧисло e, также известное как число
Эйлера, является математической
константой, приблизительно равной
2,718281828…, и может быть
охарактеризовано многими способами. Это
основа натурального логарифма. Это
предел (1 + 1/n)n по мере приближения n к
бесконечности, выражение, возникающее
при изучении сложных процентов.
7.
Десятичные логарифмы:log 10 3 lg 3
Читается:
«десятичный
логарифм 3»
lg 1 0
lg 10 1
10
lg x
x
8.
Определение логарифмаb >0
a>0, a≠1
c
b=a
с = loga b
Примеры:
log216=4,
log42=1/2,
log 1 27 3,
3
log0,254=
.
9.
Примерыlog 2 8
3 , т.к.
2 8
log 5 25 2 , т.к.
5 25
log 2 2
1 , т.к.
2 2
1
log 2 1, т.к.
2
1
2
2
1
2
3
9
1
log 3
9
2 , т.к.
3
2
1
1
10.
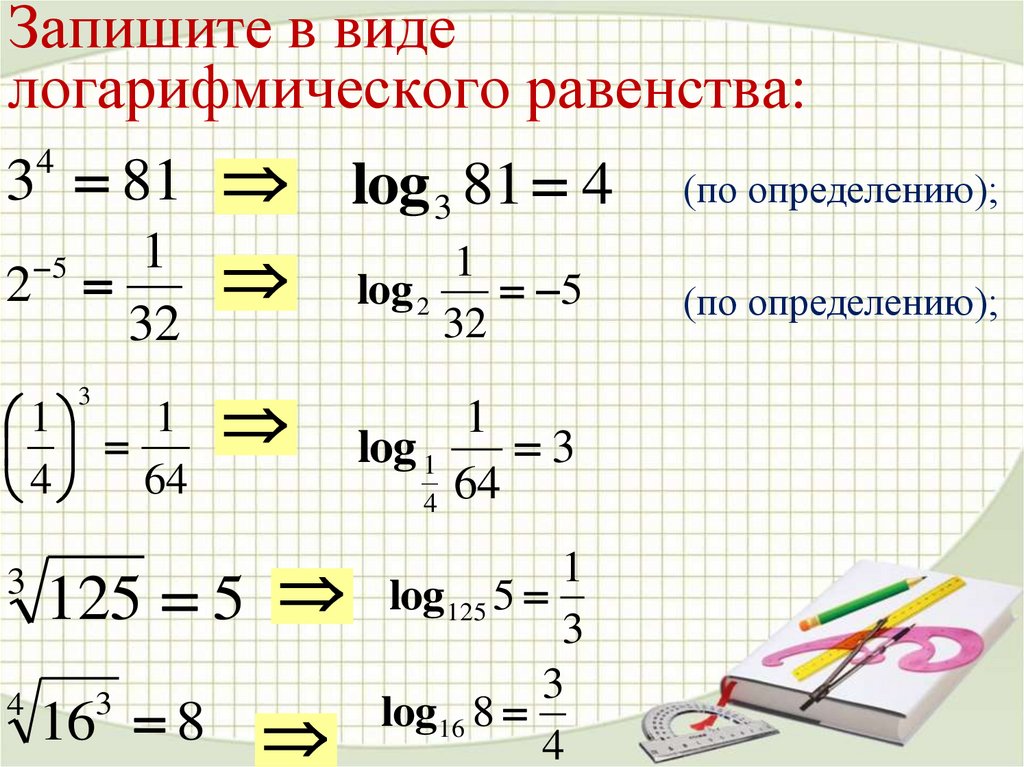
Запишите в виделогарифмического равенства:
4
3 81 log 3 81 4 (по определению);
2
5
1
32
1
log 2
5
32
3
1
log 1
3
64
4
1
1
64
4
3
125 5
4
16 8
3
1
log125 5
3
3
log16 8
4
(по определению);
11.
Примеры десятичных логарифмовlg 100
2, 10 100
lg 10
1, 10 10
lg 1
0, 10 1
lg 0,1
2
1
0
1
1, 10 0,1
lg 0,00001
5
5, 10
0,00001
12.
Пример натуральных логарифмовln e
1,
e e
1
ln e 2, e e
1
1
1
ln 1, e
e
e
2
2
log e e 1
ln e
1
2
2
ln e
3
1
3
13.
Найдите число xlog 5 x 2
2
25
x 5
log 1 x 2
6
1
x
6
x 36
2
log 3 x 1
1
x 3
1
x
3
log 5 x 0
5
x 1
x
0
14.
Найдите число xlog x 81 4
x 3
4
3 81
1
log x
2
16
log 1 x 2
1
log x 2
4
6
1
x
6
2
x 6
1
x x
4
4
2
2
2
1
4
2
x 2
15.
Вычислите1
log 2 0,25 log 2 2
4
1
2
log 1 3 3 log 1 3 3
3
3
1
log 1 3
3
1
2
3
2
1
log 1 3 log 1
3
3
3
3
2
3
2
16.
Вычислите1
3 log 7 3 1 2
7
4
2 log 5 0,04 2 log 5
100
1
2 log 5
2 2 4
25
17.
Свойства логарифмаa
loga b
b , a 0, a 1, b 0
log a 1 0
log a a 1
log a a
m
m
















 Математика
Математика








