Приложения дифференциального исчисления 17. Наибольшее и наименьшее значения функции

1. Приложения дифференциального исчисления

17. Наибольшее и наименьшее
значения функции

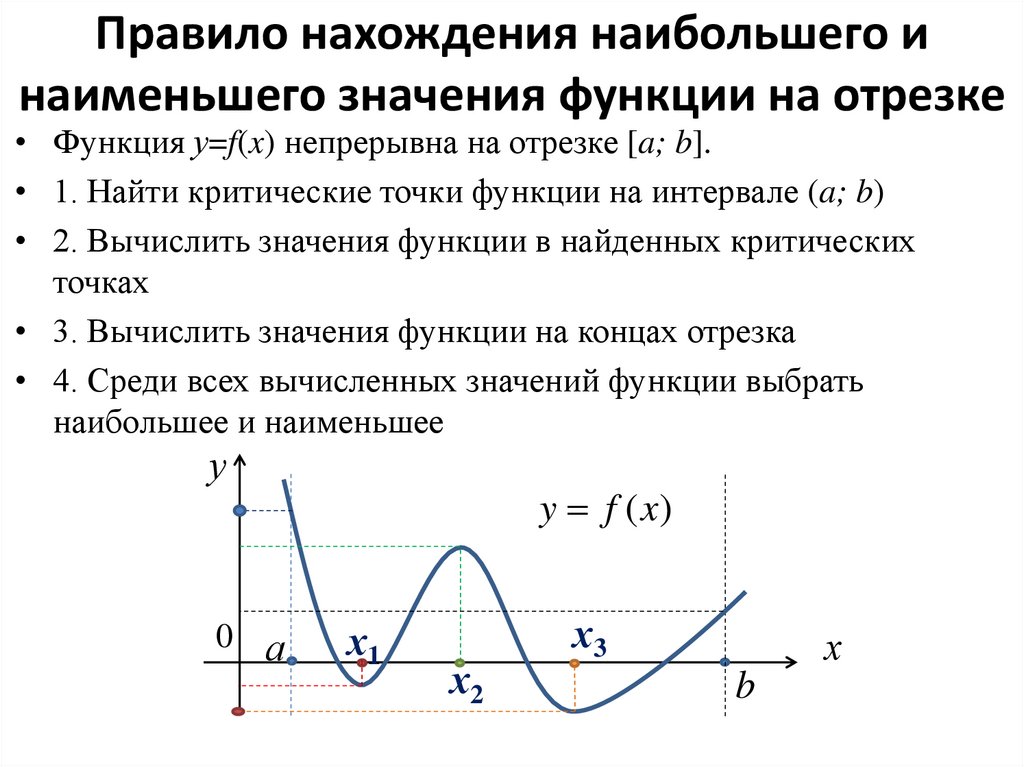
2. Правило нахождения наибольшего и наименьшего значения функции на отрезке

• Функция у=f(x) непрерывна на отрезке [a; b].
• 1. Найти критические точки функции на интервале
(a; b)
• 2. Вычислить значения функции в найденных
критических точках
• 3. Вычислить значения функции на концах отрезка
• 4. Среди всех вычисленных значений функции
выбрать наибольшее и наименьшее

3. Правило нахождения наибольшего и наименьшего значения функции на отрезке

• Функция у=f(x) непрерывна на отрезке [a; b].
• 1. Найти критические точки функции на интервале (a; b)
• 2. Вычислить значения функции в найденных критических
точках
• 3. Вычислить значения функции на концах отрезка
• 4. Среди всех вычисленных значений функции выбрать
наибольшее и наименьшее
у
0 а
y f (x)
х1
х2
х3
х
b

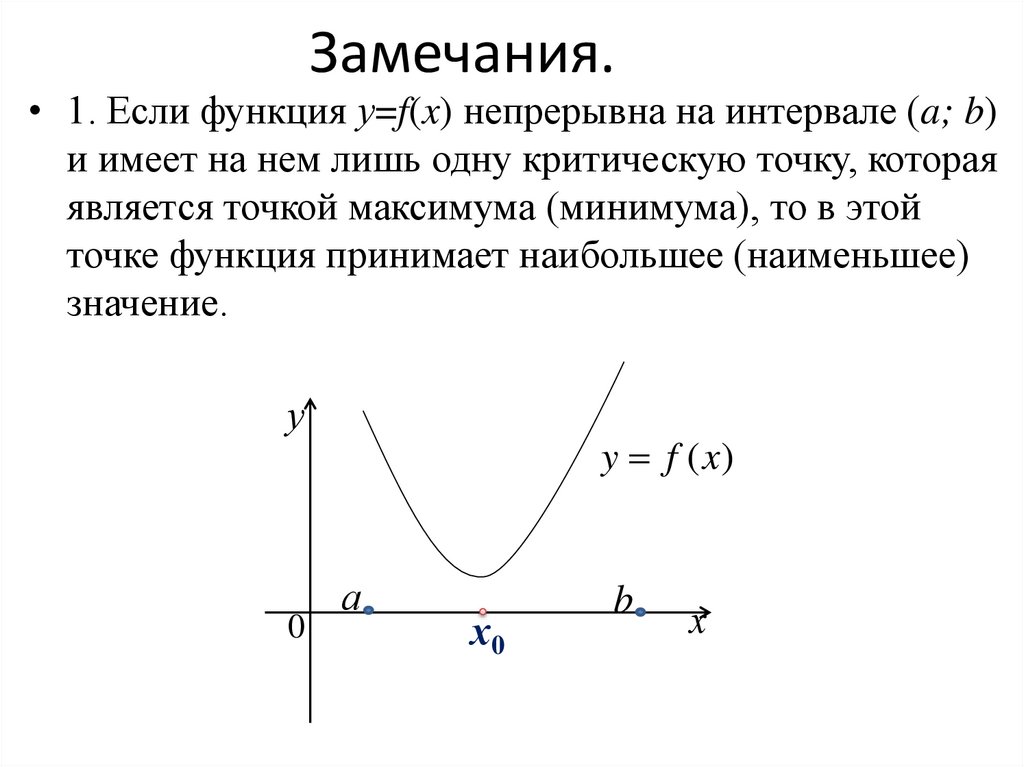
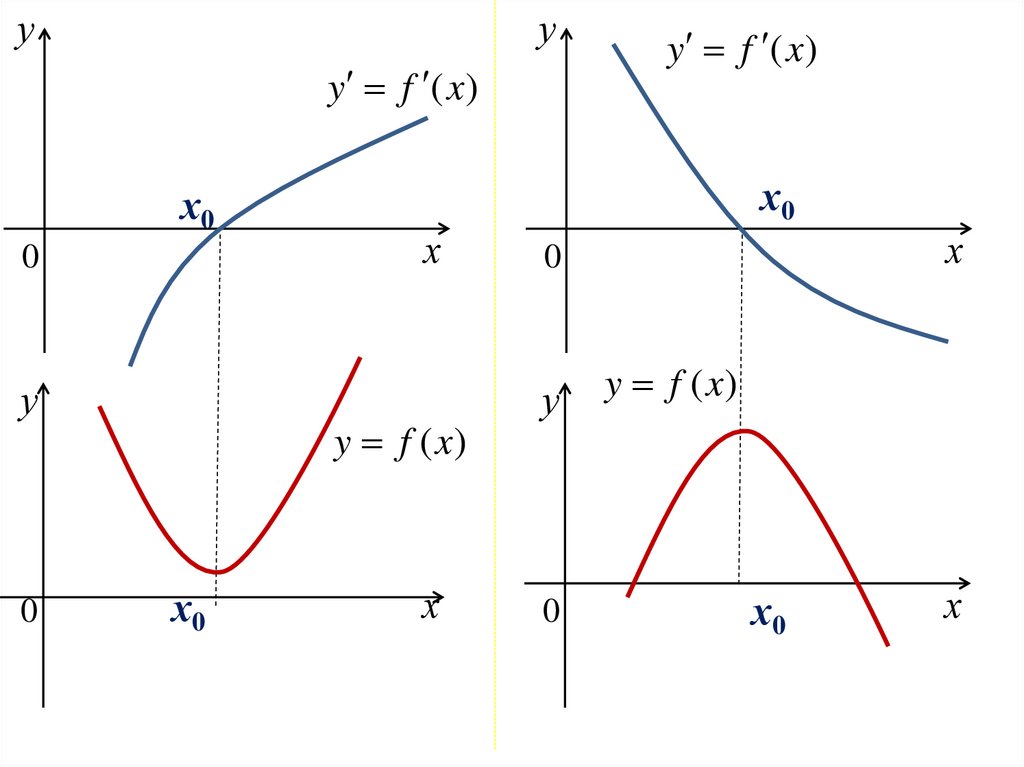
4. Замечания.

• 1. Если функция у=f(x) непрерывна на интервале (a; b)
и имеет на нем лишь одну критическую точку, которая
является точкой максимума (минимума), то в этой
точке функция принимает наибольшее (наименьшее)
значение.
у
0
y f (x)
а
х0
b
х

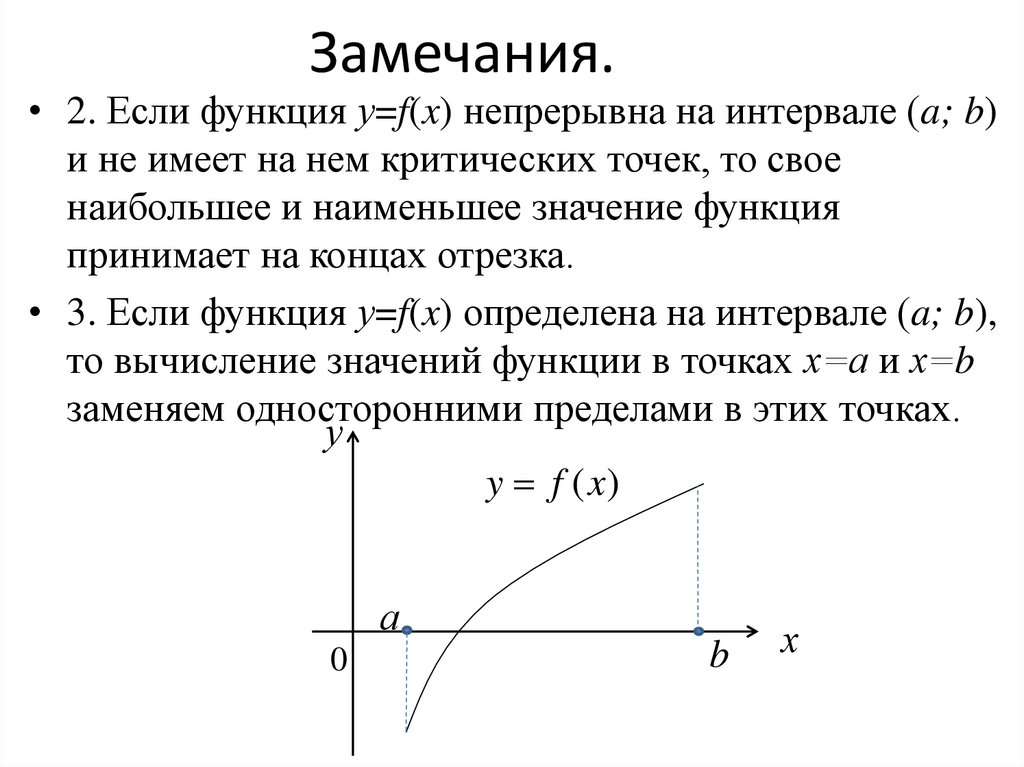
5. Замечания.

• 2. Если функция у=f(x) непрерывна на интервале (a; b)
и не имеет на нем критических точек, то свое
наибольшее и наименьшее значение функция
принимает на концах отрезка.
• 3. Если функция у=f(x) определена на интервале (a; b),
то вычисление значений функции в точках х=а и х=b
заменяем односторонними пределами в этих точках.
у
y f (x)
а
0
b
х

6. Практические (прикладные) задачи

• Указать все постоянные и переменные величины задачи.
• Выбрать из переменных одну в качестве независимой
переменной и обозначить ее х.
• Определить из условия задачи область изменения
(отрезок, интервал и т.д.) независимой переменной х.
• Выразить через выбранную переменную х
оптимизируемую величину, т.е. записать
функциональную зависимость у=f(x).
• Решить задачу на нахождение наибольшего и
наименьшего значения функции в определенной области.
• Выбирать наибольшее или наименьшее значение, исходя
из условий задачи. Ответить на вопрос задачи.

7. Упрощения при исследовании на экстремум

y k f ( x) b, k , b const
y f (x)
k 0
k 0
y ( f ( x)) , n N , n 2
y f (x)
f ( x) 0
y n f ( x) , n N
y f (x)
f ( x) 0
1
y
f ( x)
y f (x)
f ( x) 0
n

8. Практические (прикладные) задачи

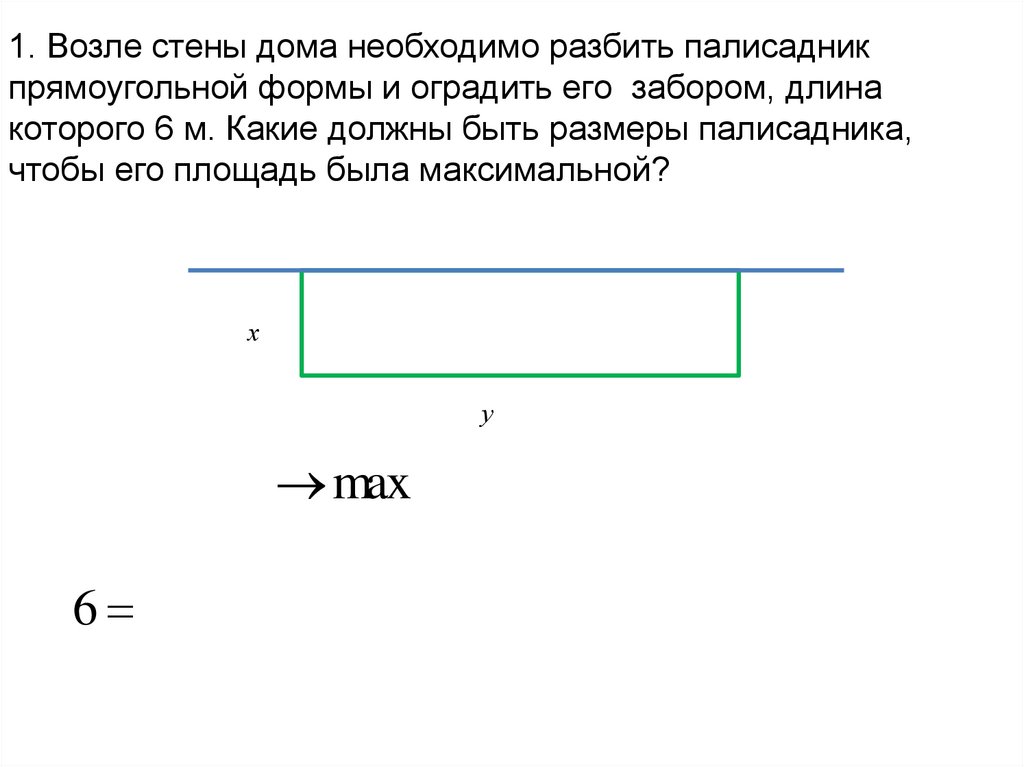
• 1. Возле стены дома необходимо разбить
палисадник прямоугольной формы и
оградить его забором, длина которого 6 м.
Какие должны быть размеры палисадника,
чтобы его площадь была максимальной?

9.

1. Возле стены дома необходимо разбить палисадник
прямоугольной формы и оградить его забором, длина
которого 6 м. Какие должны быть размеры палисадника,
чтобы его площадь была максимальной?
х
у
max
6

10.

1. Возле стены дома необходимо разбить палисадник
прямоугольной формы и оградить его забором, длина
которого 6 м. Какие должны быть размеры палисадника,
чтобы его площадь была максимальной?
х
у
S x y max
2x y 6
y 6 2x
S ( x) x (6 2 x) max
x

11.

1. Возле стены дома необходимо разбить палисадник
прямоугольной формы и оградить его забором, длина
которого 6 м. Какие должны быть размеры палисадника,
чтобы его площадь была максимальной?
х
у
S ( x ) x (6 2 x ) 6 x 2 x
2
2
S ( x) (6 x 2 x ) 6 4 x
6 4x 0
3
3
x
y 6 2 3
2
2
0 x 3

12.

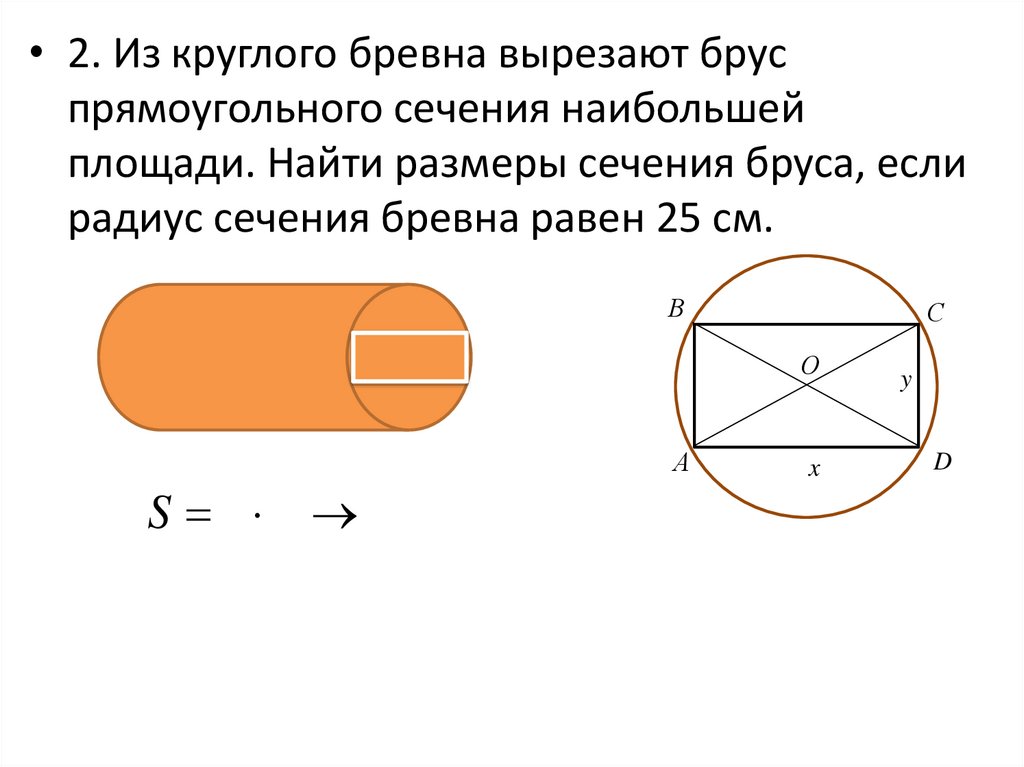
• 2. Из круглого бревна вырезают брус
прямоугольного сечения наибольшей
площади. Найти размеры сечения бруса, если
радиус сечения бревна равен 25 см.
В
С
О
А
S
x
y
D

13.

• 2. Из круглого бревна вырезают брус
прямоугольного сечения наибольшей площади.
Найти размеры сечения бруса, если радиус
сечения бревна равен 25 см.
S x y max
0 x 50
S ( x) x 2500 x
2
В
С
О
А
2500 x x
2500 x
2
D
x
2
S ( x) x 2500 x x 2500 x
2
y
2
2500 x 2
2500 x
2

14.

• 2. Из круглого бревна вырезают брус
прямоугольного сечения наибольшей площади.
Найти размеры сечения бруса, если радиус
сечения бревна равен 25 см.
S ( x) x 2500 x
S (x )
2
2500 2 x 2
2500 x 2
0 x 50
0
x 25 2
x 2 1250
y
В
С
О
А
y
D
x
x 35,4
2500 1250 25 2
S (x ) x
2
S 1250 (см )
2

15. Практические (прикладные) задачи

• 3. Требуется огородить забором площадку
прямоугольной формы площадью 36 см2.
36 см2

16. Практические (прикладные) задачи

• 4. Окно имеет форму прямоугольника,
завершенного полукругом. Периметр окна равен
Р. Найти размеры сторон прямоугольника, при
которых окно будет пропускать наибольшее
количество света.

17. Практические (прикладные) задачи

• 5. Из шара радиуса R выточить цилиндр
наибольшего объема. Каковы его размеры?

18. Задачи с экономическим смыслом

• Производитель реализует свою продукцию по цене
50у.е. за единицу, а издержки при этом задаются
кубической зависимостью
x3
S ( x) x
12
• Найти оптимальный для производства объем выпуска
продукции и соответствующую ему прибыль.
• Решение.
• Доход от выпускаемой продукции объема х
• D(x)= 50 x
• Функция прибыли C ( x) D ( x) S x

19.

• Производитель реализует свою продукцию по цене
50у.е. за единицу, а издержки при этом задаются
кубической зависимостью
x3
S ( x) x
12
• Найти оптимальный для производства объем выпуска
продукции и соответствующую ему прибыль.
• Решение. Функция прибыли
3
x
C ( x) 50 x x
12
3
x
C ( x) 50 x x
12
x2
Cmax ( x0 )
x

20. Эластичность функции

• Эластичностью функции Ех(у) называется
предел отношения относительного приращения
функции у к относительному приращению
переменной х при Δх→0:
y x x
E x ( y ) lim
: y
x 0
y x y
• Эластичностью функции показывает
приближенно, на сколько процентов изменится
функция у=f(x) при изменении независимой
переменной х на 1%.

21.

• Зависимость между себестоимостью единицы
продукции у (тыс.руб.) и выпуском продукции
х (млн.руб.) выражается функцией
y 0,5 x 80
• Найти эластичность себестоимости при
выпуске продукции, равном 60 млн.руб.
• Решение.
x
Ex ( y)
y
y
E x 60 ( y )
При выпуске продукции, равном 60 млн.руб., увеличение его на 1% приведет к
себестоимости на
?
%
?

22.

у
у
y f (x)
х0
0
у
0
х0
х
y f (x)
х0
y f (x)
х
х
0
у
0
y f (x)
х0
х

23.

у
у
y f (x)
х0
0
y f (x)
х0
х
у
х
0
у
y f (x)
0
х0
х
y f (x)
0
х0
х

24.

у
у
y f (x)
y f (x)
х
0
0
х0
х
х0
у
y f (x)
у
y f (x)
0
х0
х
0
х0
х