Похожие презентации:
Плоскости. Взаимное расположение точки, прямой и плоскости
1.
Лекция 3. Плоскости.Взаимное расположение
точки, прямой и плоскости.
Инженерная и компьютерная графика Б1.В.07
09.03.01. Информатика и вычислительная техника
Доцент Ткачук Евгений Остапович
2019/2020
2.
Плоскость• 1. Плоскость есть поверхность, содержащая
полностью каждую прямую, соединяющую любые
ее точки;
• 2. Плоскость есть множество точек,
равноотстоящих от двух заданных точек.
• Общее уравнение плоскости:
• Ax+By+Cz+D=0,
• где А, В, С, и D - постоянные, причём А, В и С
одновременно не равны нулю.
3.
Способы задания плоскостей• тремя точками, не лежащими на одной прямой линии
• прямой линией и точкой, не принадлежащей этой прямой
• двумя пересекающимися прямыми
• двумя параллельными прямыми
4.
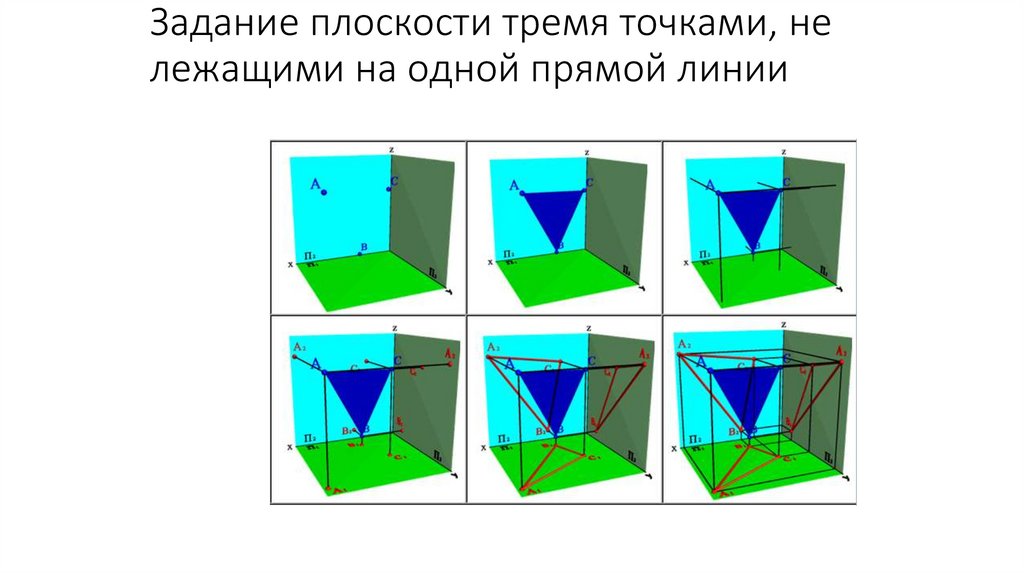
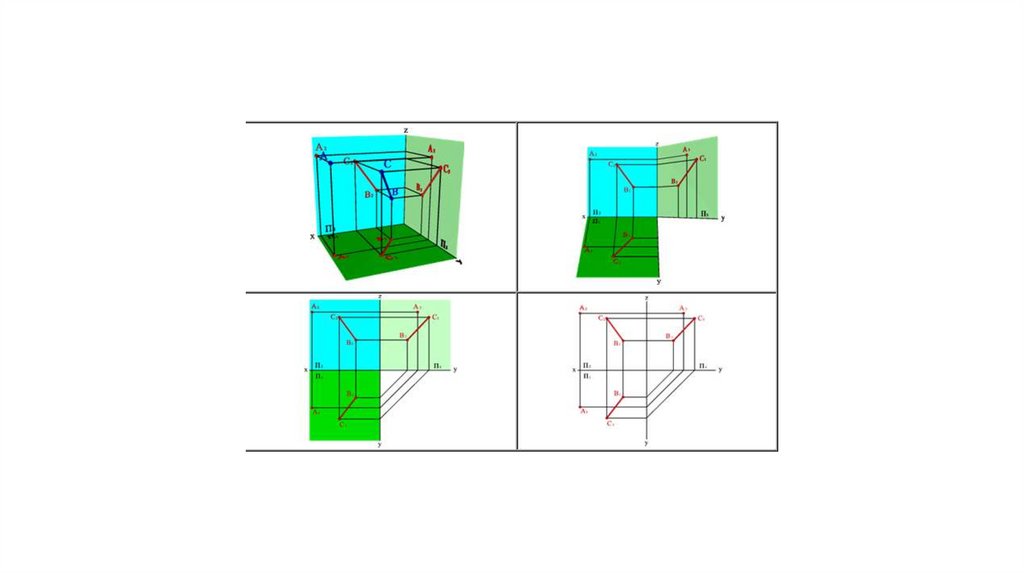
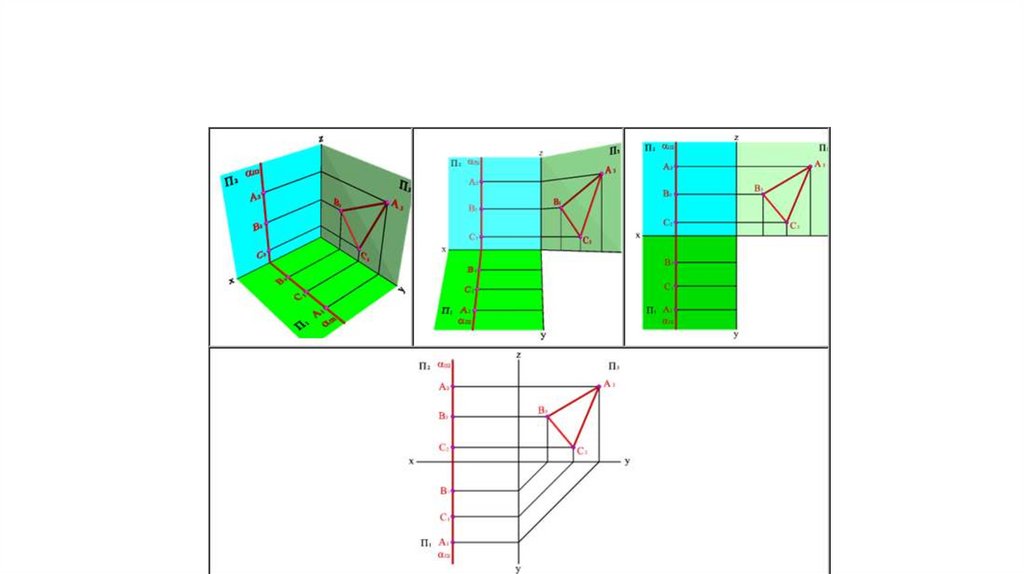
Задание плоскости тремя точками, нележащими на одной прямой линии
5.
6.
Задание плоскости прямой линией иточкой, не принадлежащей этой
прямой
7.
8.
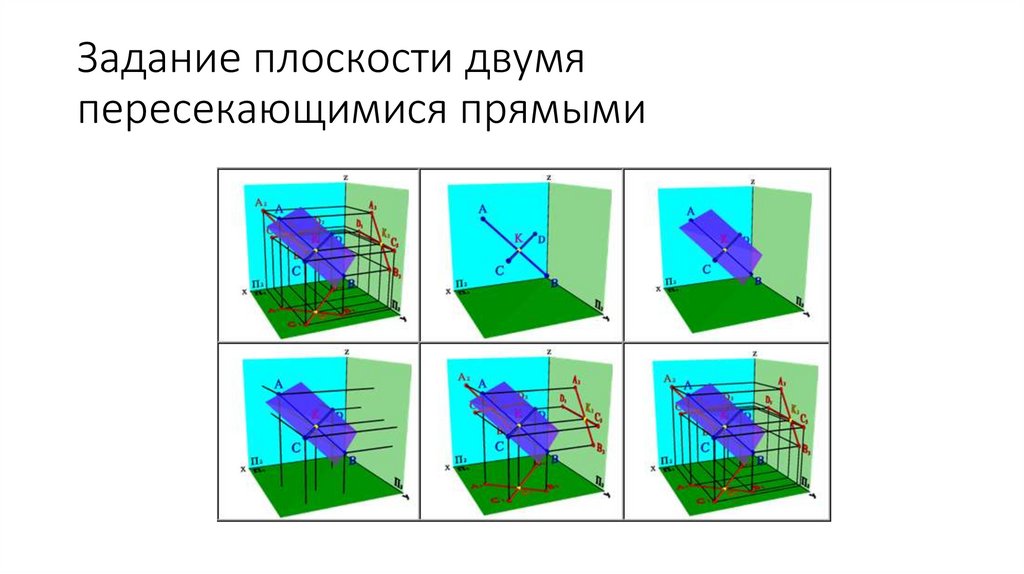
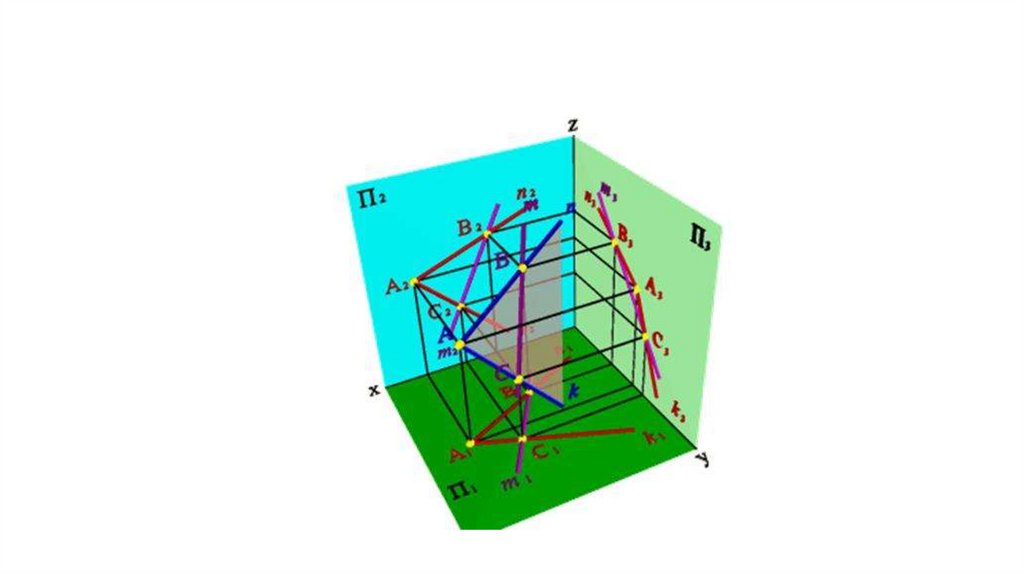
Задание плоскости двумяпересекающимися прямыми
9.
10.
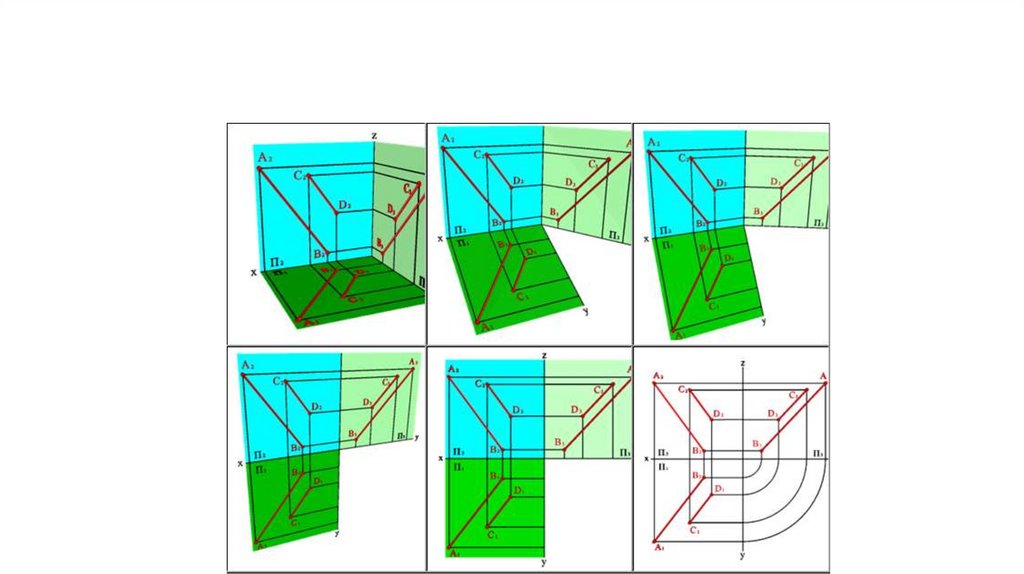
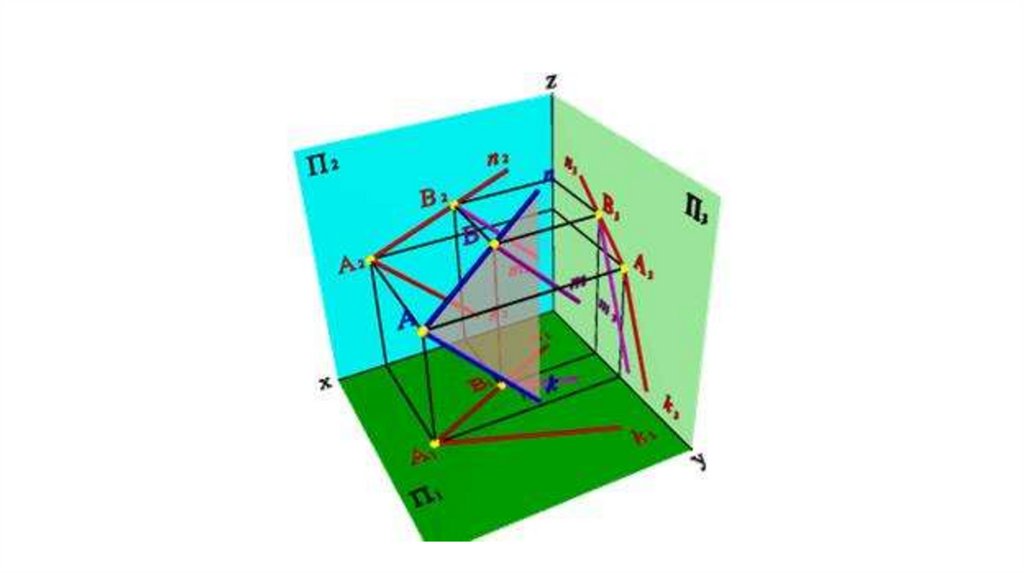
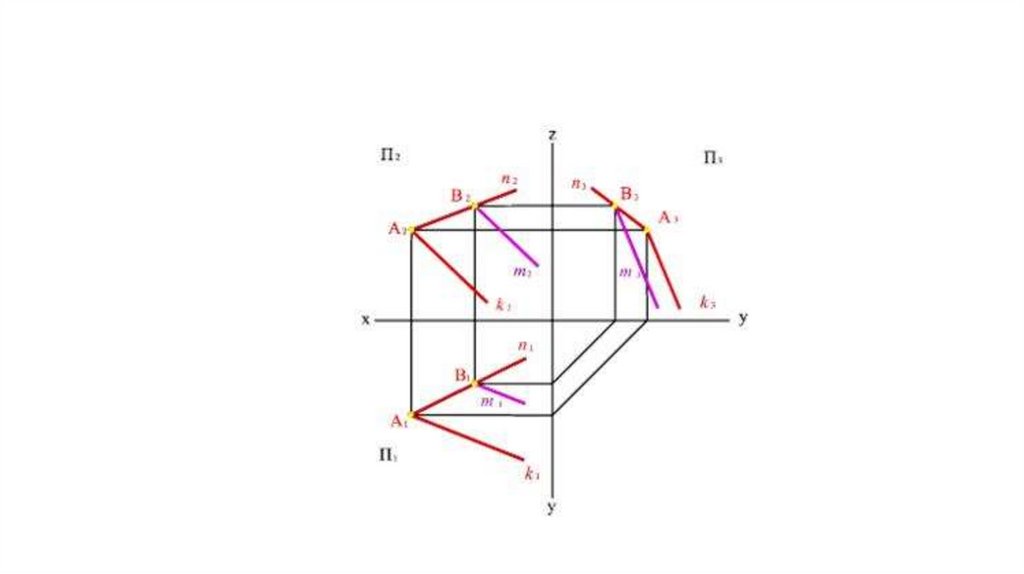
Задание плоскости двумя параллельнымипрямыми
11.
12.
Следом плоскости…• называется прямая линия, по которой
плоскость пересекается с плоскостью
проекций.
• В зависимости от того, какую плоскость
проекций пересекает данная α плоскость
различают:
• горизонтальный αП1,
• фронтальный αП2
• профильный αП3 следы.
13.
14.
Положение плоскости относительноплоскостей проекций
• 1. Плоскость не перпендикулярная ни одной плоскости
проекций называется плоскостью общего
положения. Такая плоскость пересекает все плоскости
проекций (имеет три следа: - горизонтальный П1; фронтальный П2; - профильный П3).
• 2. Плоскости, перпендикулярные плоскостям проекций –
занимают частное положение в пространстве и называются
проецирующими. В зависимости от того, какой плоскости
проекций перпендикулярна заданная плоскость, различают:
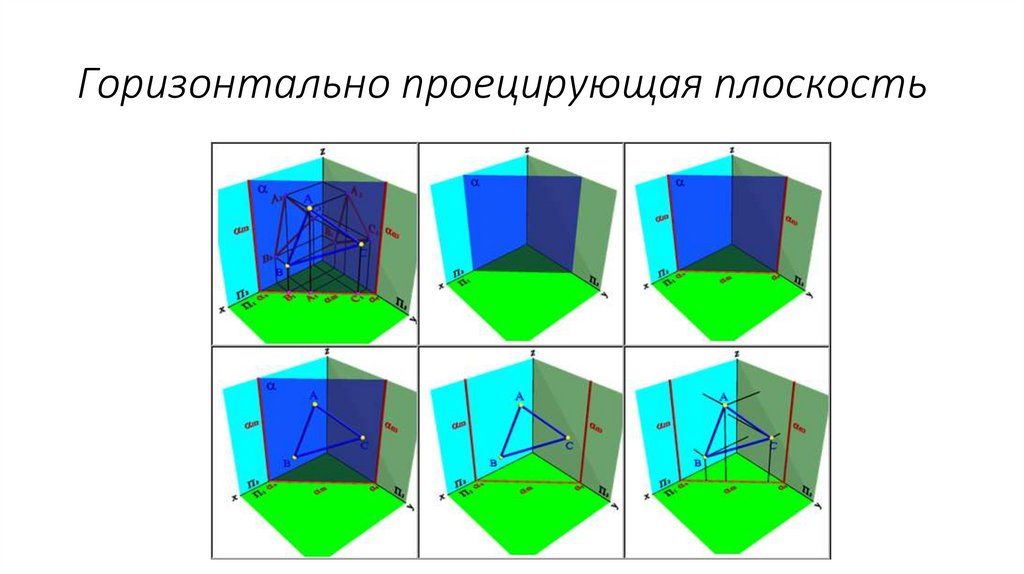
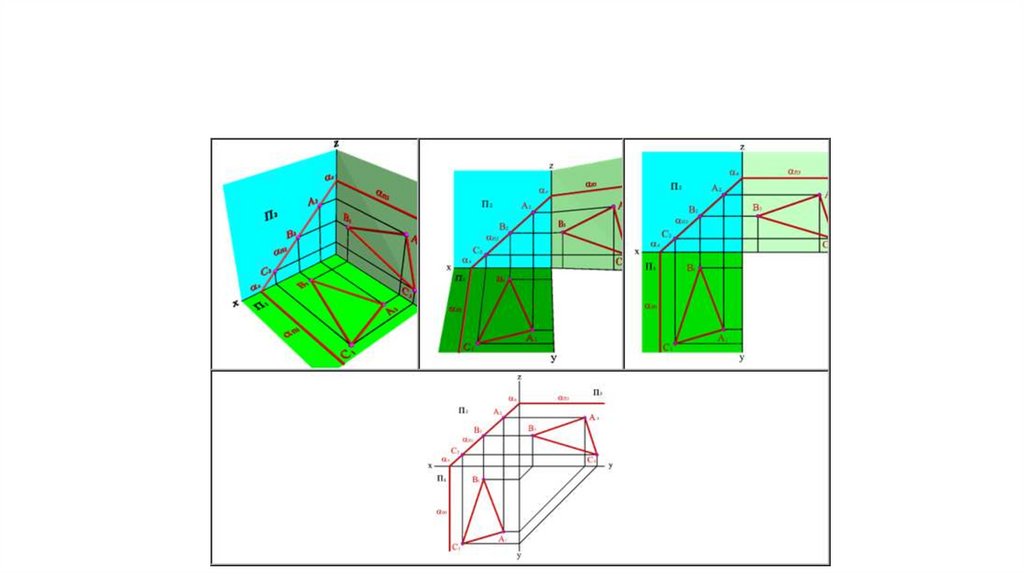
• 2.1. Плоскость, перпендикулярная горизонтальной
плоскости проекций П , называется горизонтально
проецирующей плоскостью. Горизонтальная проекция
такой плоскости представляет собой прямую линию,
которая одновременно является её горизонтальным
следом. Горизонтальные проекции всех точек этой
плоскости совпадают с горизонтальным следом
15.
Горизонтально проецирующая плоскость16.
17.
Фронтально проецирующая плоскость18.
19.
Биссекторная плоскость20.
Плоскости, параллельные плоскостямпроекций называются плоскостями
уровня
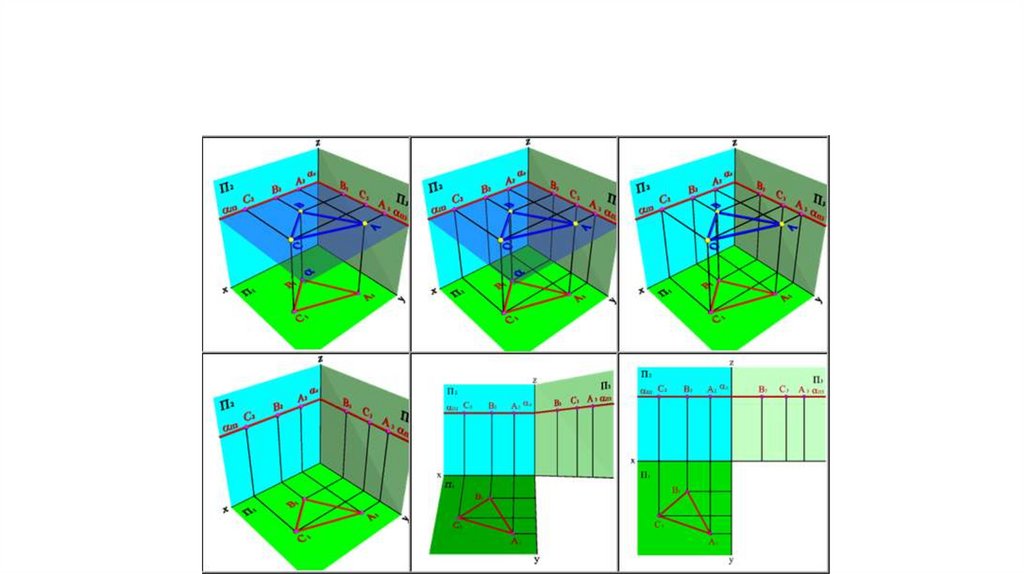
• 3.1. Горизонтальная плоскость - плоскость, параллельная
горизонтальной плоскости проекций ( П1) - ( П2, П3).
Геометрический объект, принадлежащий этой плоскости
проецируется на плоскость П1 без искажения, а на плоскости П2 и
П3 в прямые - следы плоскости П2 и П3
21.
Горизонтальная плоскость22.
23.
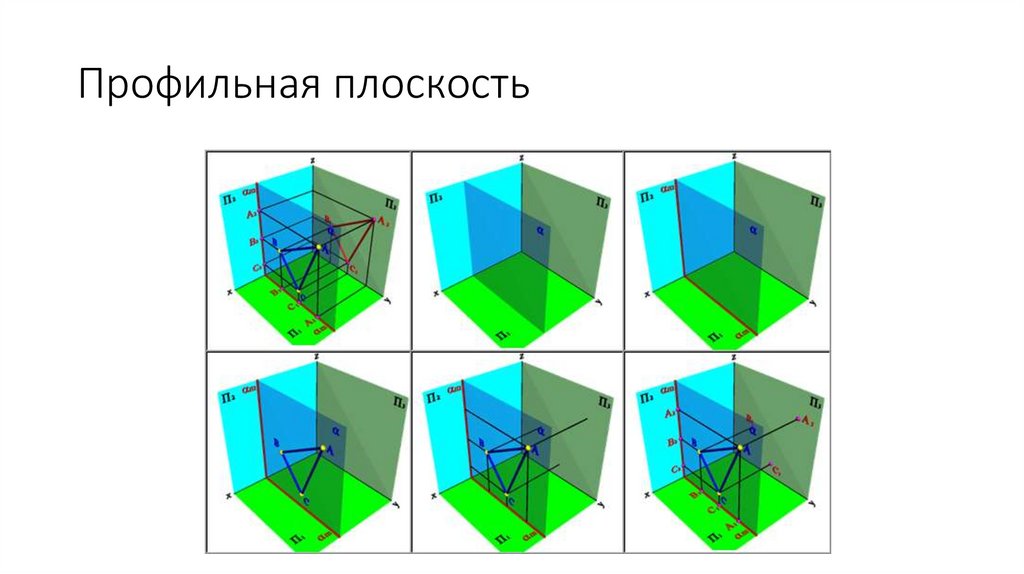
Профильная плоскость• плоскость, параллельная профильной плоскости проекций
( //П3), ( П1, П2). Геометрический объект, принадлежащий
этой плоскости проецируется на плоскость П3 без искажения, а на
плоскости П1 и П2 в прямые - следы плоскости П1 и П2
24.
Профильная плоскость25.
26.
Следы плоскости• Следом плоскости называется линия пересечения
плоскости с плоскостью проекций. В зависимости,
от того с какой из плоскостей проекций
пересекается данная плоскость, различают:
горизонтальный, фронтальный и профильный
следы плоскости.
27.
Построение следов плоскости28.
Построение следов плоскости29.
Взаимное расположение прямой иплоскости
• Известны три варианта взаимного расположения прямой и
плоскости:
• Прямая принадлежит плоскости.
• Прямая параллельна плоскости.
• Прямая пересекает плоскость.
30.
условие принадлежности прямойплоскости
• Аксиома 1. Прямая принадлежит плоскости, если две её точки
принадлежат этой плоскости.
• Аксиома 2. Прямая принадлежит плоскости, если имеет с
плоскостью одну общую точку и параллельна какой-либо прямой
расположенной в этой плоскости.
31.
Задача• Дана плоскость (n,k) и одна проекция прямой m2
• Требуется найти недостающие проекции прямой m, если
известно, что она принадлежит плоскости, заданной
пересекающимися прямыми n и k.
32.
33.
Прямая и плоскость имеют две общиеточки
34.
Прямая и плоскость имеют две общиеточки
35.
Прямая и плоскость имеют две общиеточки
36.
Задача.• Через точку В провести прямую m, если известно, что она
принадлежит плоскости заданной пересекающимися прямыми n
иk
37.
38.
39.
40.
41.
Главные линии плоскости• Горизонтали h - прямые, лежащие в данной плоскости и
параллельные горизонтальной плоскости проекций (h АВС
h h Ох,h Оy)
42.
43.
44.
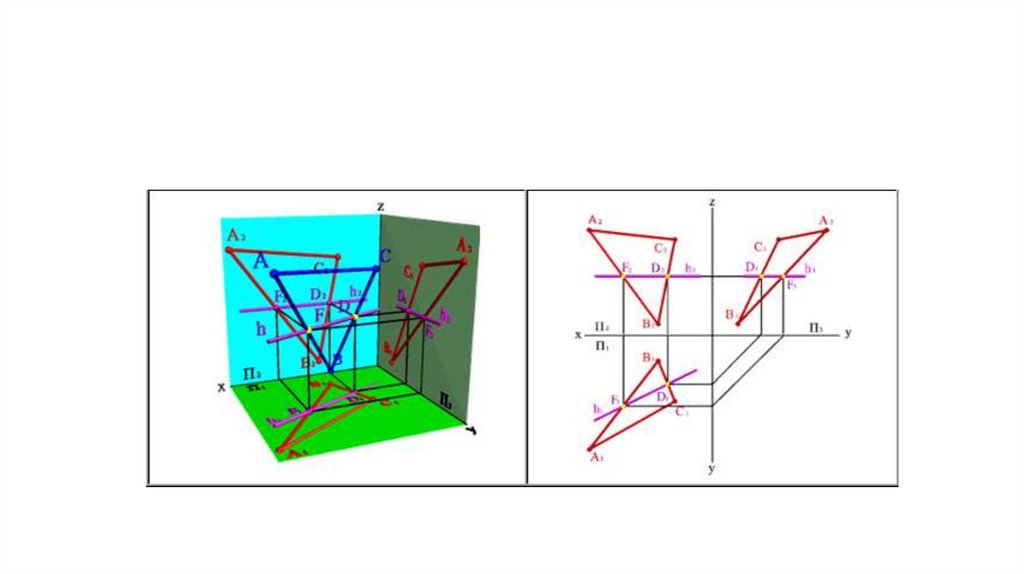
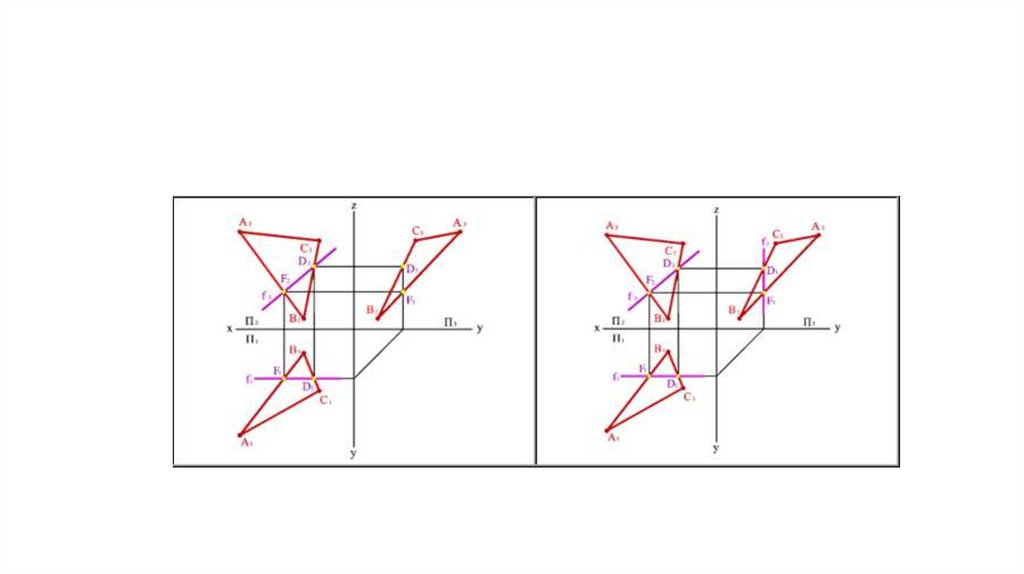
• Фронтали f - прямые, расположенные вплоскости и параллельные фронтальной
плоскости проекций (f АВС f f Ох, f Оz)
45.
46.
47.
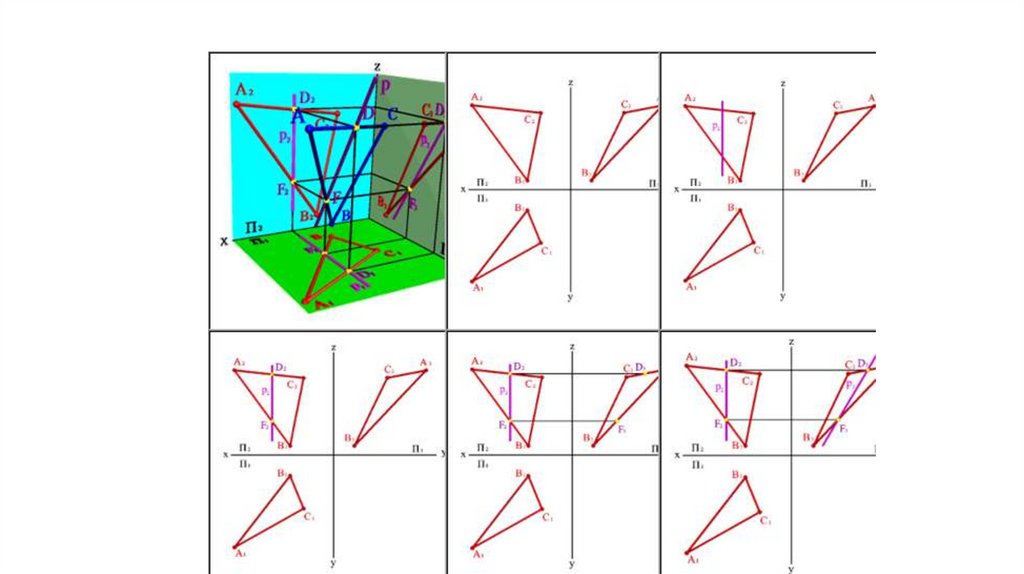
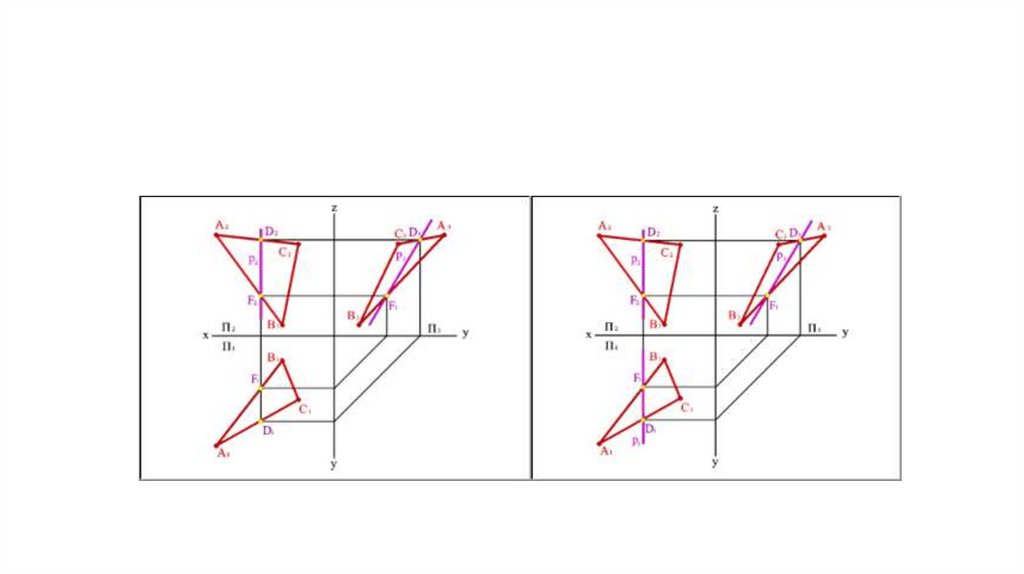
• Профильные прямые р - прямые, которыенаходятся в данной плоскости и параллельны
профильной плоскости проекций (р АВС р
р1 Ох р Ох)
48.
49.
50.
• Прямые, принадлежащие плоскости и образующие с плоскостьюпроекций наибольший угол называются линиями наибольшего
наклона данной плоскости к плоскости проекций
• Линия наибольшего наклона к горизонтальной плоскости
проекций называется линией ската.
51.
52.
53.
Прямая, параллельная плоскости• При решении вопроса о параллельности прямой линии и
плоскости необходимо опираться на известное положение
стереометрии: прямая параллельна плоскости, если она
параллельна одной из прямых, лежащих в этой плоскости и не
принадлежит этой плоскости.
54.
• Задача. Дано: плоскость общего положения ABC и прямая общегоположения а.
55.
56.
57.
58.
• Для этого через прямую а проведем вспомогательную секущуюплоскость - в данном случае горизонтально проецирующая
плоскость. Найдем линию пересечения плоскостей и АВС прямую п (DF). Проекция прямой п на горизонтальную плоскость
проекций совпадает с проекцией а1 и со следом плоскости .
Проекция прямой п2 параллельна а2, п3 параллельна а3,
следовательно, прямая а параллельна плоскости AВС.
59.
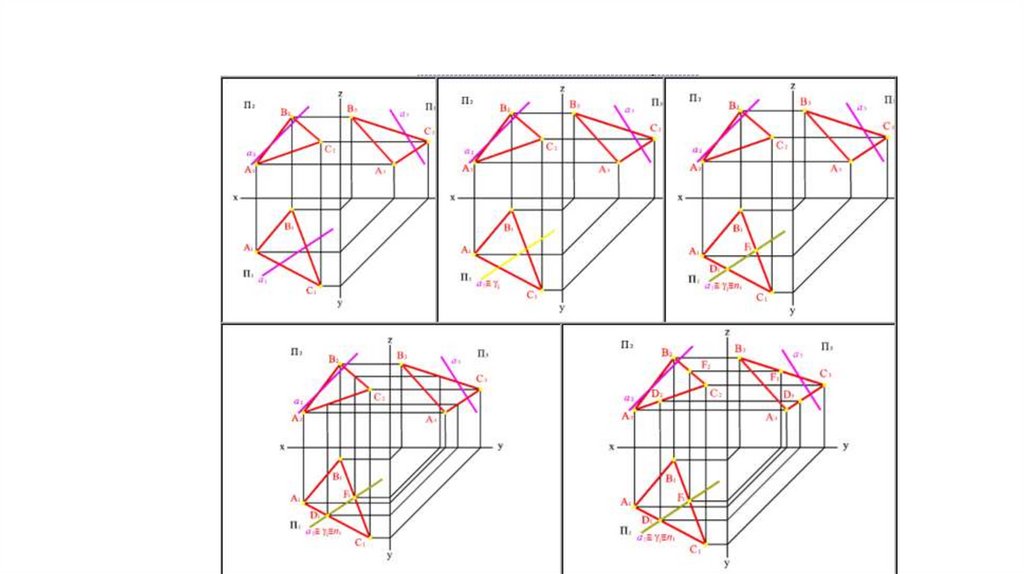
Прямая пересекает плоскость• Дано: плоскость AВС и прямая а.
• Алгоритм решения задачи (рис.60):
• Через горизонтальную проекцию прямой а1 проведем
вспомогательную горизонтально проецирующую плоскость (таким
образом а ).
• Находим линию пересечения вспомогательной плоскости с заданной.
Горизонтальный след плоскости 1 пересекает проекцию плоскости
A1В1С1 в точках D1 и F1, которые определяют положение
горизонтальной проекции п1- линии пересечения плоскостей и AВС.
Для нахождения фронтальной и профильной проекции п спроецируем
точки D и F на фронтальную и профильную плоскости проекций.
60.
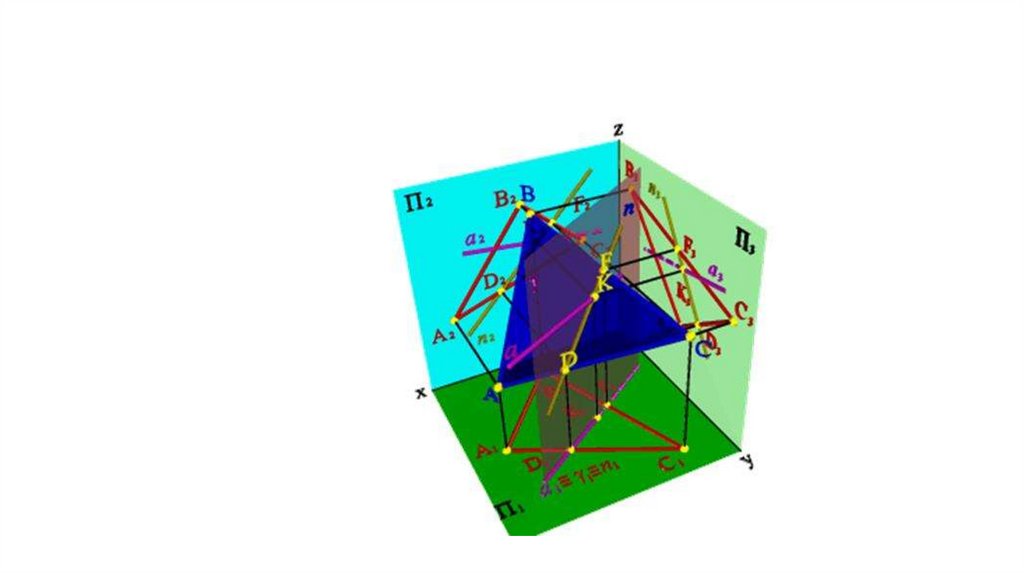
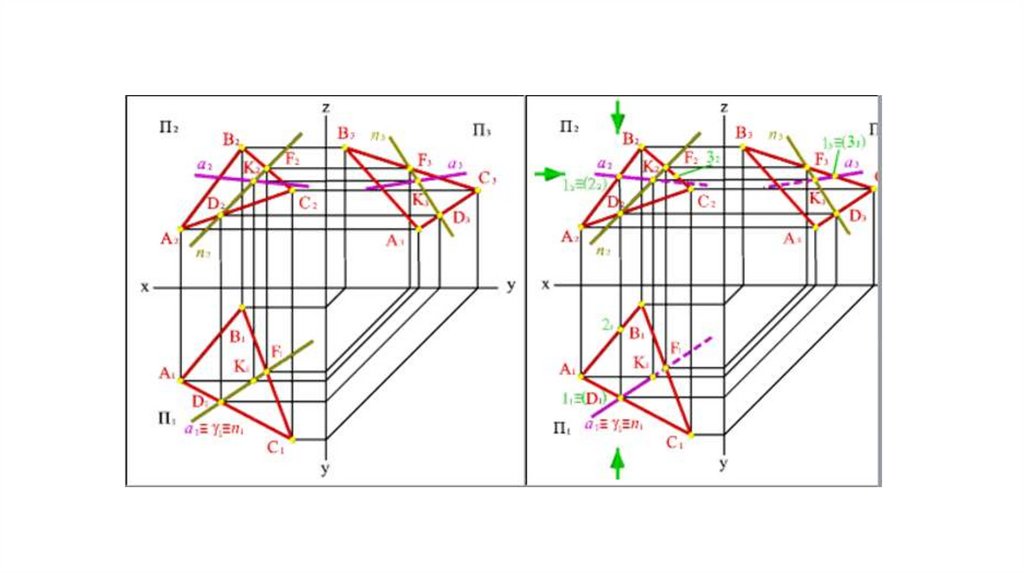
• Определяем точку пересечения прямых а и п. На фронтальной ипрофильной проекциях линия пересечения плоскостей п
пересекает проекции а в точке К, которая и является проекцией
точки пересечения прямой а с плоскостью AВС, по линии связи
находим горизонтальную проекцию К1.
• Методом конкурирующих точек определяем видимость прямой а
по отношению к плоскости AВС.
61.
62.
63.
64.
65.
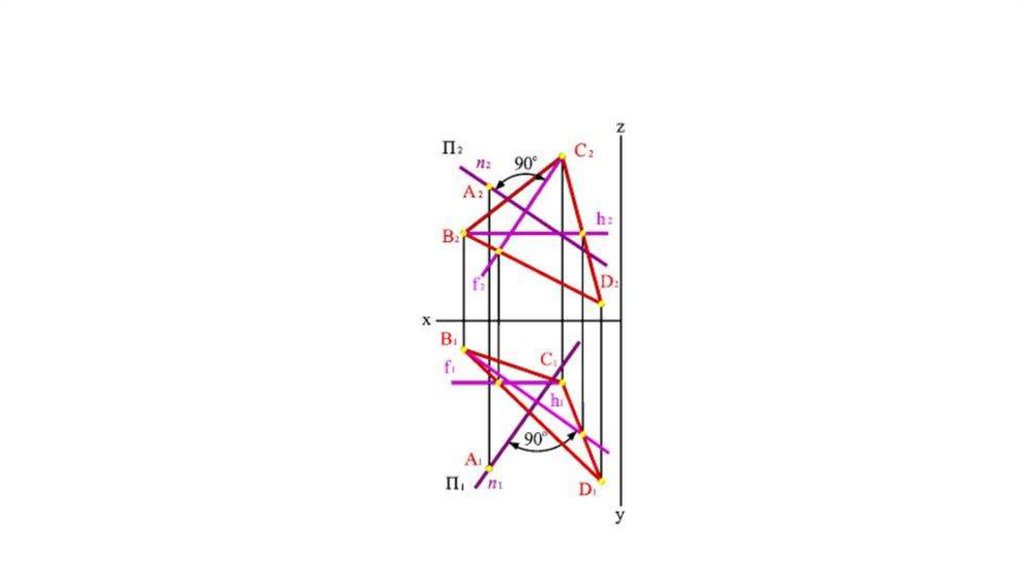
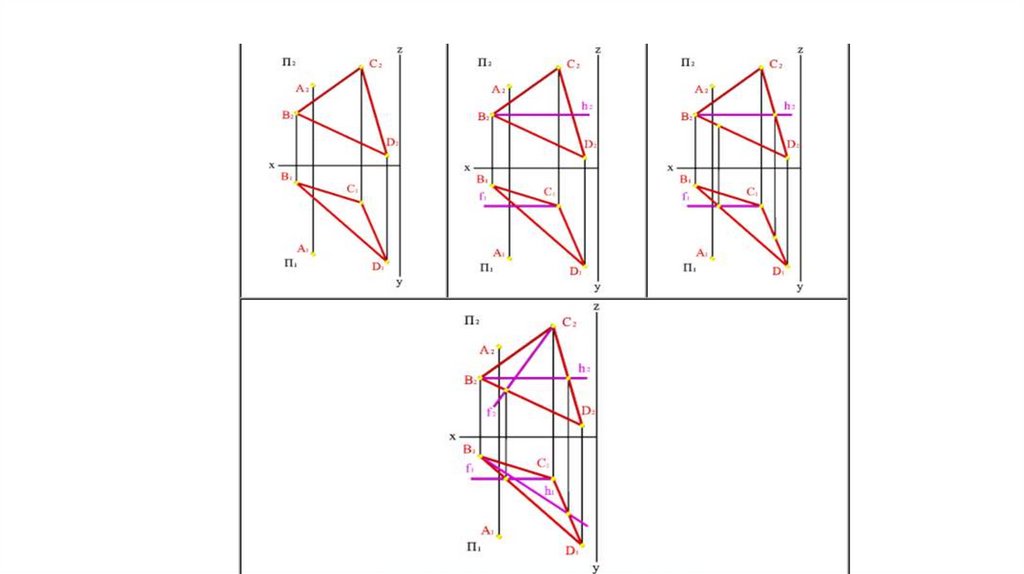
Прямая, перпендикулярная плоскости• Теорема о перпендикуляре к плоскости:
• Если прямая перпендикулярна плоскости, то
горизонтальная проекция этой прямой
перпендикулярна горизонтальной проекции
горизонтали плоскости, а фронтальная проекция –
фронтальной проекции фронтали плоскости.
66.
• Задача. Дано: плоскость ВСD и точка А.• Требуется построить прямую линию n проходящую через точку А
и перпендикулярную плоскости ВСD.
67.
68.
69.
• В плоскости ВСD построим фронталь f и горизонтальh. В горизонтальной плоскости проекций проведем
через точку А1 прямую n1 перпендикулярно
горизонтальной проекции горизонтали h1, а на
фронтальной плоскости проекций через точку А2
прямую n2 перпендикулярно фронтальной проекции
фронтали f2, согласно, теореме о перпендикуляре к
плоскости, полученная прямая n будет
перпендикулярна плоскости ВСD.
70.
71.
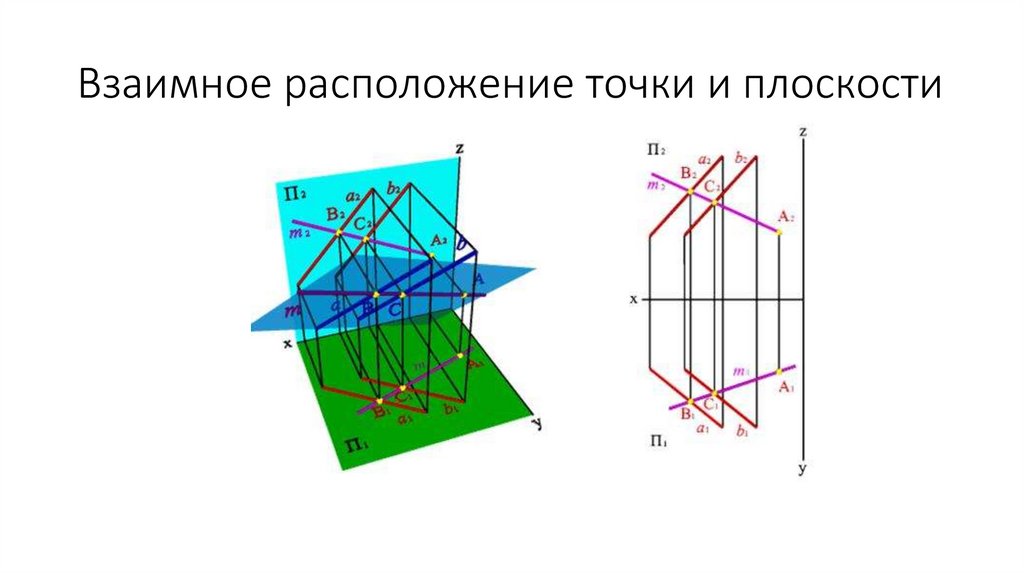
Взаимное расположение точки и плоскости72.
73.
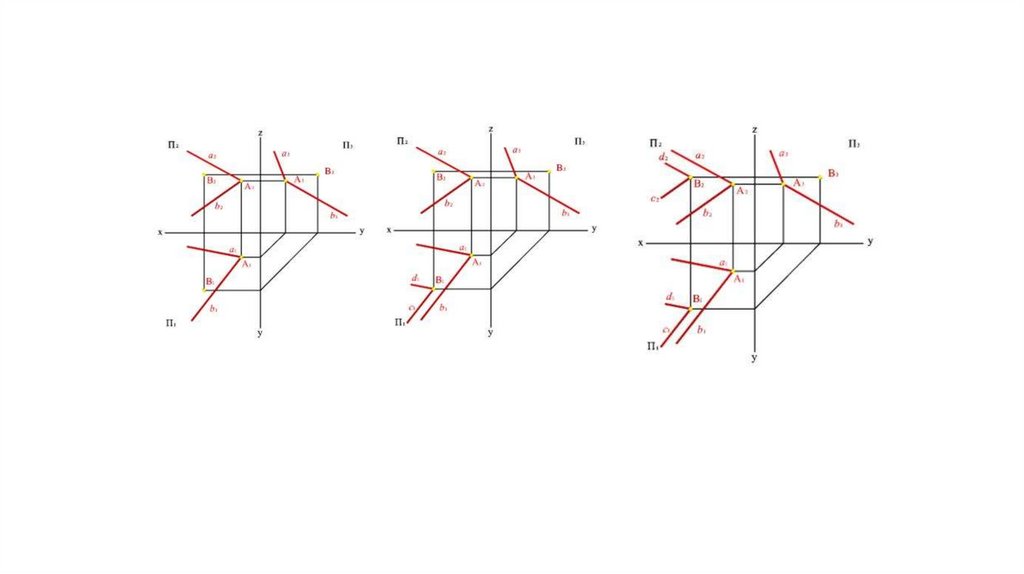
Взаимное расположение плоскостей• Две плоскости в пространстве могут быть либо параллельны, в
частном случае совпадать друг с другом, либо пересекаться.
Взаимно перпендикулярные плоскости представляют собой
частный случай пересекающихся плоскостей
74.
75.
76.
пересекающиеся плоскости77.
78.
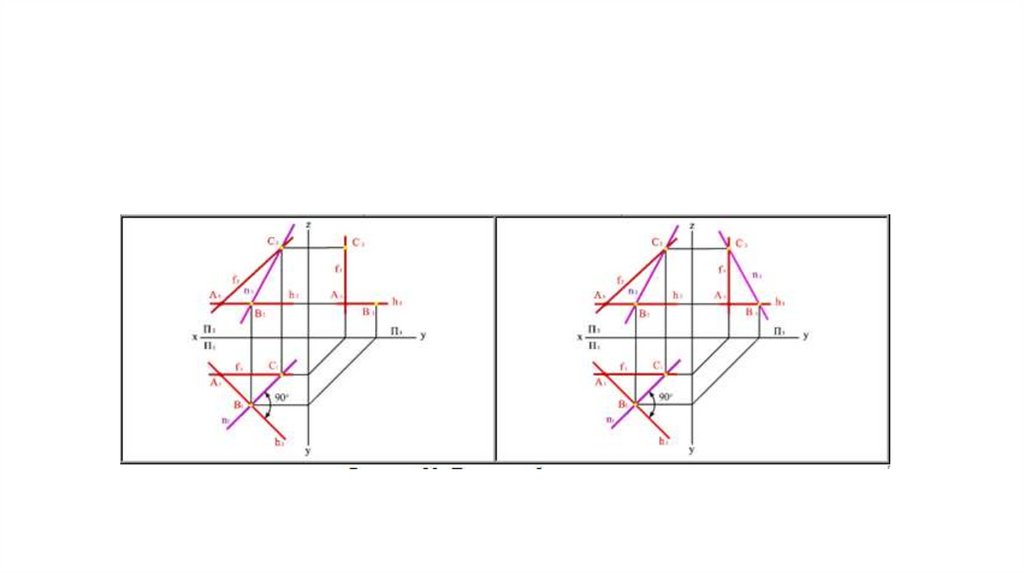
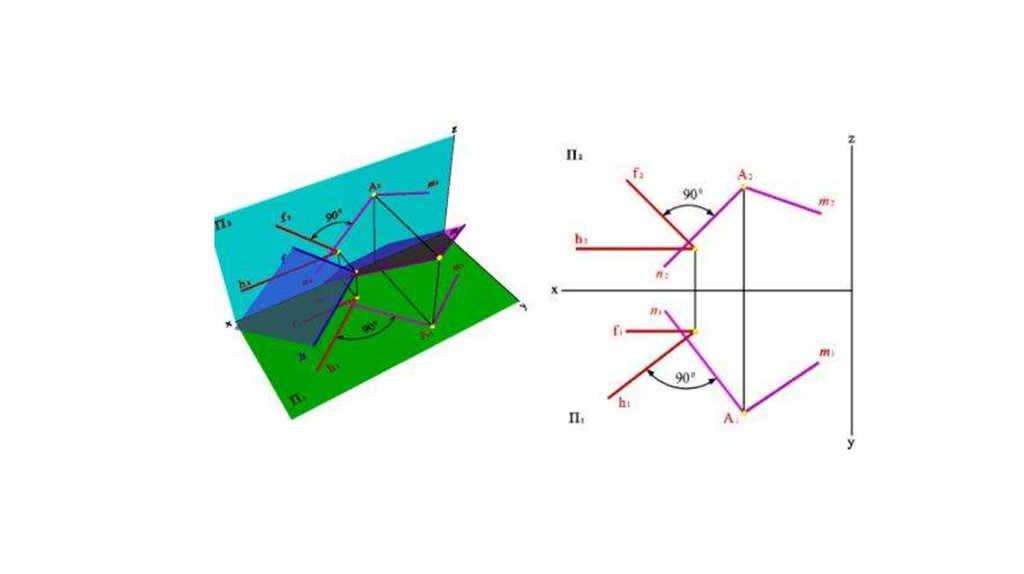
Взаимно перпендикулярные плоскости• Частный случаем пересечения плоскостей являются взаимно
перпендикулярные плоскости.
• Из стереометрии известно, что две плоскости взаимно
перпендикулярны, если одна из них проходит через
перпендикуляр к другой. Через точку А можно провести
множество плоскостей, перпендикулярных данной плоскости
(h,f).























































 Инженерная графика
Инженерная графика








