Прямокутні координати в просторі

1.

z
1
1
x
О
1
y

2.

у
о
х

3.

ВІДВІДУЮЧИ ПАРИЗЬКІ ТЕАТРИ,
ДЕКАРТ НЕ ВТОМЛЮВАВСЯ
ДИВУВАТИСЯ ПУТАНИНІ,
СУПЕРЕЧКАМ, А ЧАСОМ І
ВИКЛИКАМ НА ДУЕЛЬ, ЯКІ
ВИКЛИКАЛИСЯ ВІДСУТНІСТЮ
ЕЛЕМЕНТАРНОГО ПОРЯДКУ
РОЗПОДІЛУ ПУБЛІКИ В ЗАЛІ ДЛЯ
ГЛЯДАЧІВ.
ВІН ЗАПРОПОНУВАВ СИСТЕМУ
НУМЕРАЦІЇ, В ЯКІЙ КОЖНЕ
МІСЦЕ ОТРИМУВАЛО НОМЕР
РЯДУ І ПОРЯДКОВИЙ НОМЕР ВІД
КРАЮ.
ВОНА ВІДРАЗУ ЗНЯЛА ВСІ
ПРИВОДИ ДЛЯ СУПЕРЕЧОК І
ВИКЛИКАЛА СПРАВЖНІЙ ФУРОР.
ЦЕЙ МЕТОД НУМЕРАЦІЇ КРІСЕЛ У
ГЛЯДАЦЬКІЙ ЗАЛІ ПО РЯДАМ І
МІСЦЯМ ЗБЕРЕЖЕНИЙ І
СЬОГОДНІ.
у
№
Р
Я
Д
А
х
№ МІСЦЯ У РЯДІ

4.

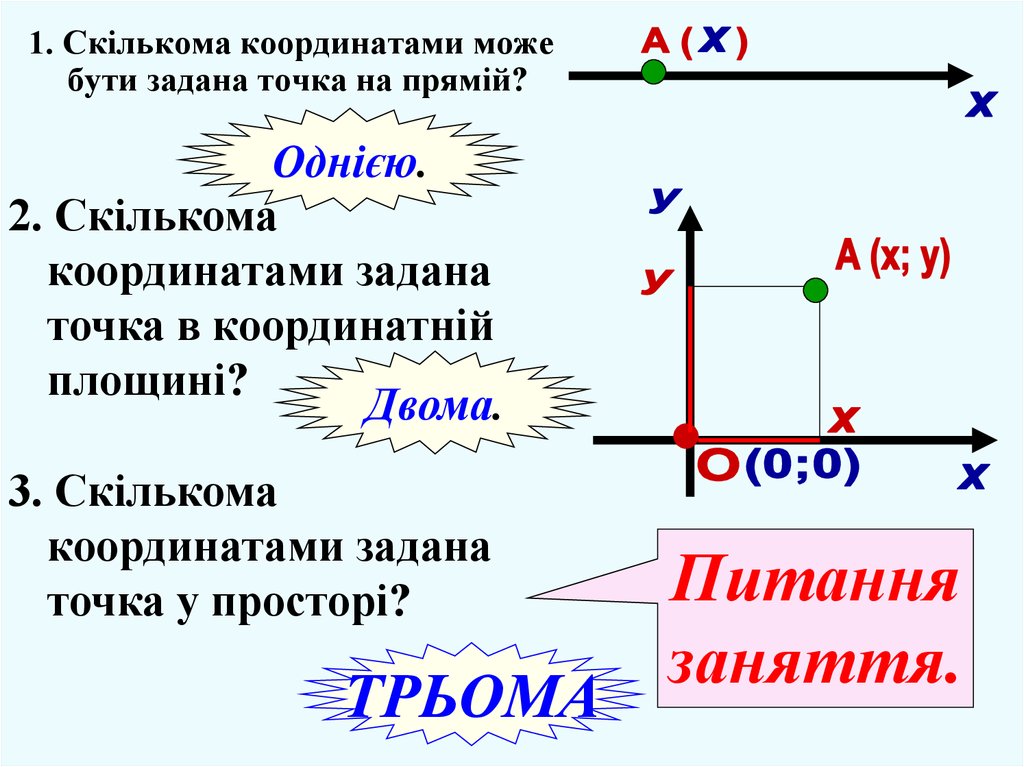
1. Скількома координатами може
бути задана точка на прямій?
Однією.
2. Скількома
координатами задана
точка в координатній
площині?
Двома.
3. Скількома
координатами задана
точка у просторі?
ТРЬОМА
Питання
заняття.

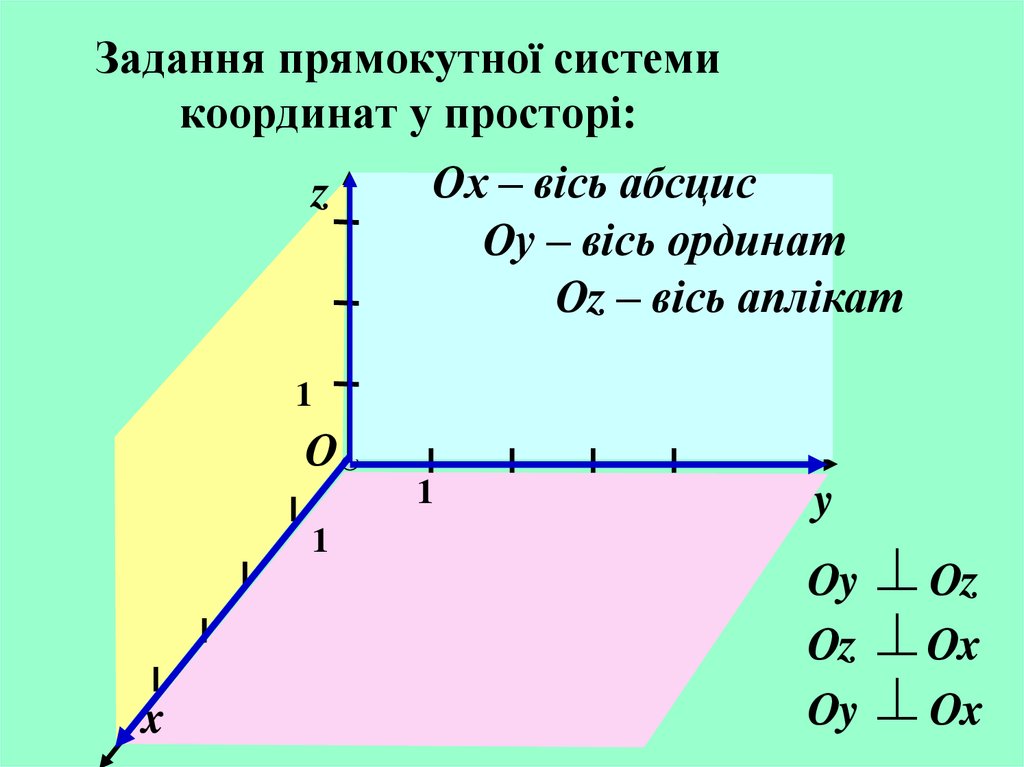
5. Задання прямокутної системи координат у просторі:

z
Ох – вісь абсцис
Оу – вісь ординат
Оz – вісь аплікат
1
О
1
1
x
y
Оy
Оz
Оy
Оz
Оx
Оx

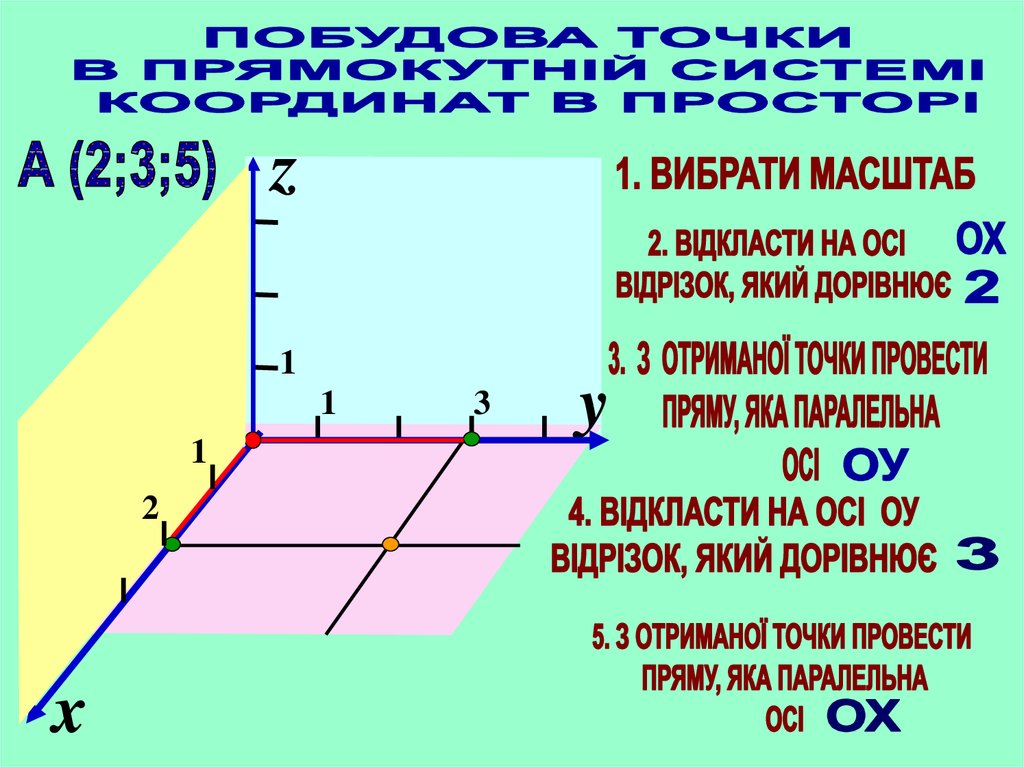
6.

z
О
1
2
x
1
1
3
y

7.

z
1
3
О
2
x
1
1
y

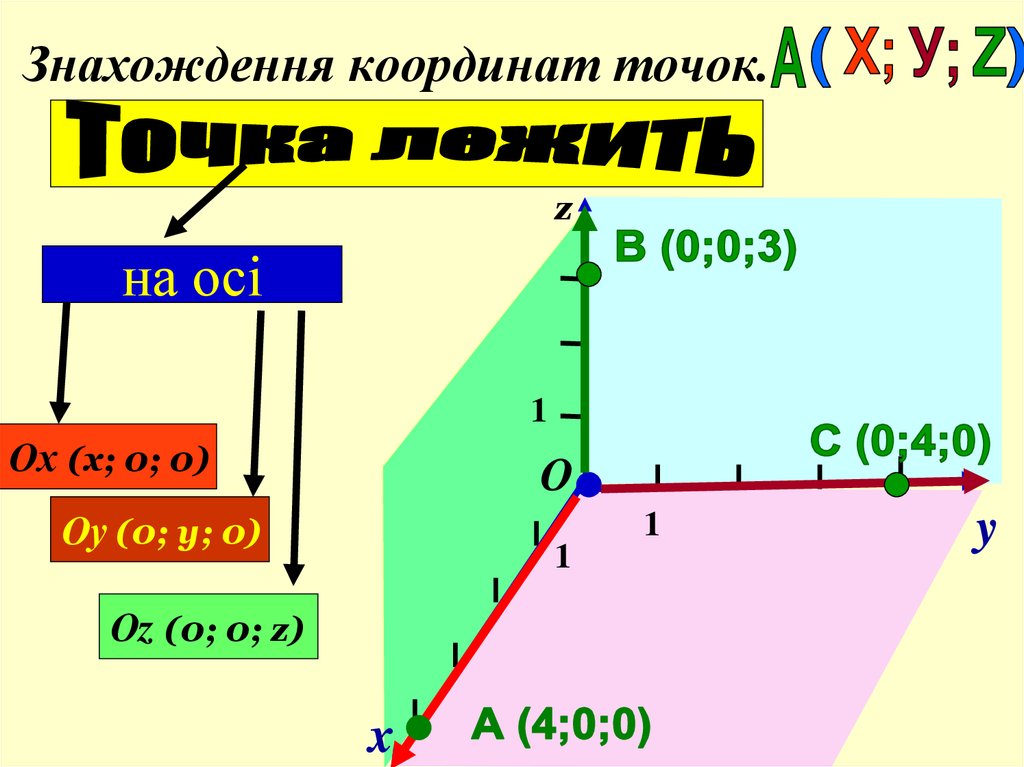
8. Знахождення координат точок.

z
на осі
1
Ох (х; 0; 0)
О
Оу (0; у; 0)
1
1
Оz (0; 0; z)
x
y

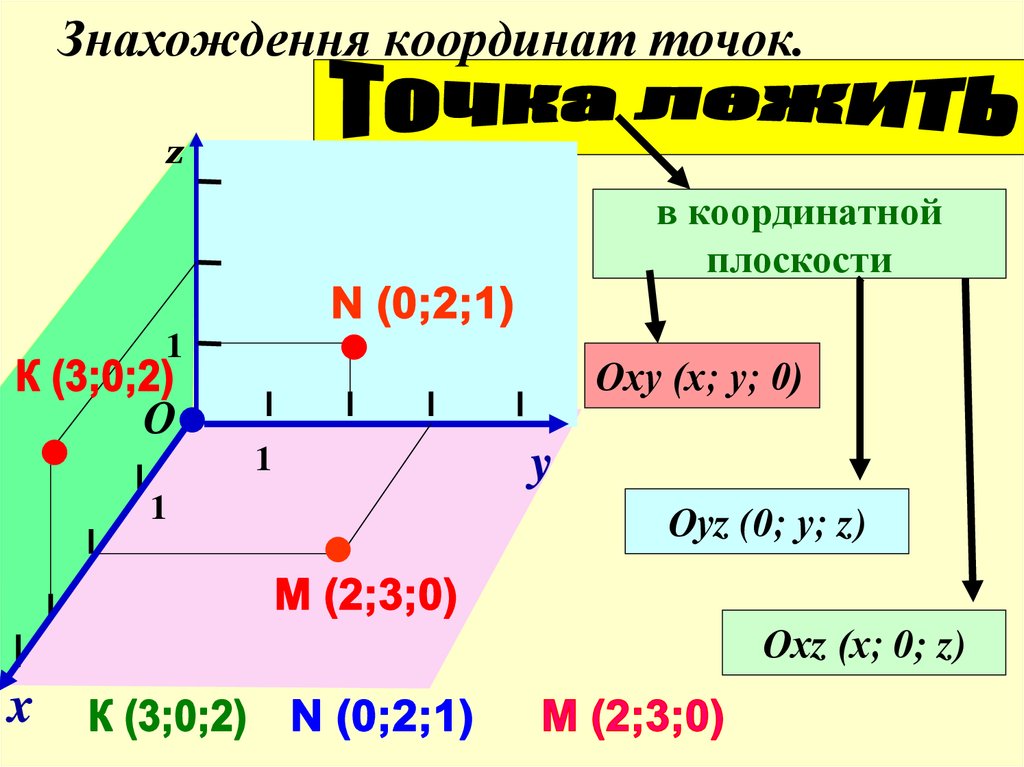
9. Знахождення координат точок.

z
в координатной
плоскости
1
Оху (х; у; 0)
О
1
1
y
Оуz (0; у; z)
Охz (х; 0; z)
x

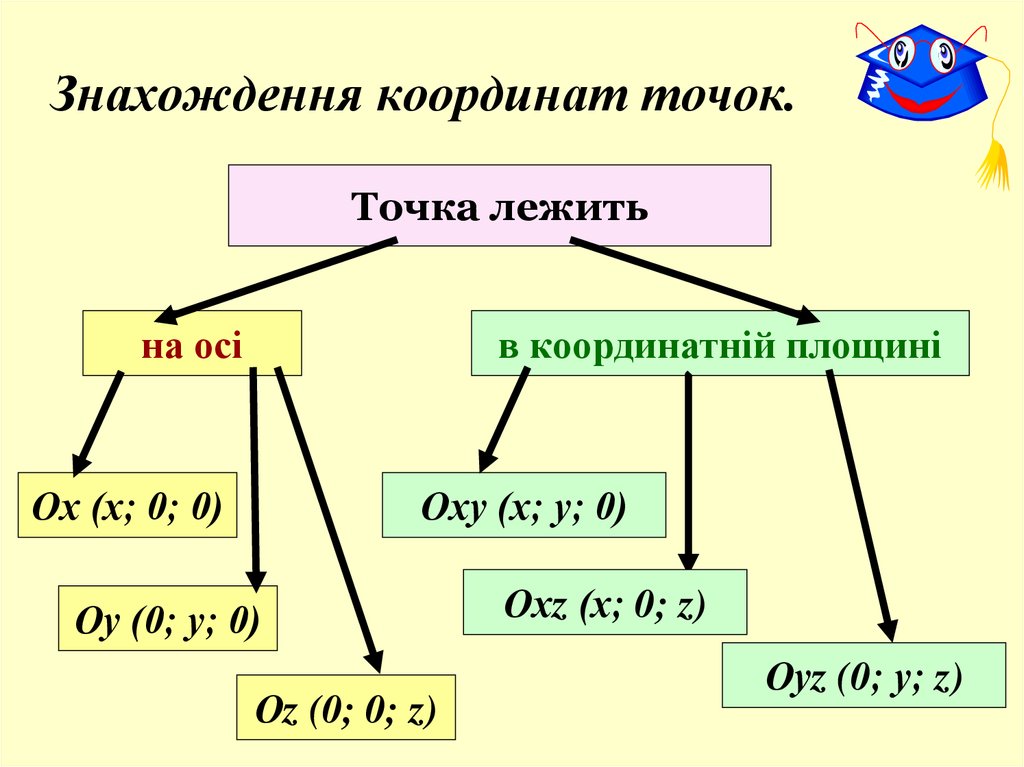
10. Знахождення координат точок.

Точка лежить
на осі
в координатній площині
Ох (х; 0; 0)
Оху (х; у; 0)
Оу (0; у; 0)
Оz (0; 0; z)
Охz (х; 0; z)
Оуz (0; у; z)

11.

z
1
О
1
1
x
y

12.

ПІД ЯКИМ КУТОМ
ЯК НАЗИВАЮТЬ
ПЕРЕТИНАЮТЬСЯ
ТОЧКУ ПЕРЕТИНУ
КООРДИНАТНІ
КООРДИНАТНИХ
ПРЯМІ
ПРЯМИХ:
У ПРОСТОРІ:
А) ПІД
ОСТРИМ
А) ПІД
ОСТРИМ
КУТОМ;
КУТОМ;
Б)ПІД ПРЯМИМ
Б) ПІД ПРЯМИМ
КУТОМ
КУТОМ; ;
В)ПІД
В)
ПІД ТУПИМ
ТУПИМ КУТОМ;
КУТОМ;
Г) ПІД РАЗГОРНУТИМ
КУТОМ
КУТОМ
А) ПОЧАТОК
А) ПОЧАТОК ВСІХ
ВСІХ
ПОЧАТКІВ;
ПОЧАТКІВ;
Б) СЕРЕДИНА;
Б) СЕРЕДИНА;
В) ПОЧАТОК
В) ПОЧАТОК
КООРДИНАТ;
КООРДИНАТ;
Г) РОЗДІЛЬНИК
Г) РОЗДІЛЬНИК
ЯК
НАЗИВАЮТЬСЯ
(Х; У; Z)
ДЛЯ ТОЧКИ
У ПРОСТОРІ:
А) КООРДИНАТИ
ТОЧКИ;
А)КООРДИНАТИ
ТОЧКИ;
Б) ЧИСЛА
У ПРОСТОРІ;
Б)ЧИСЛА У ПРОСТОРІ;
В) ЧИСЛА
ДЛЯ ТОЧКИ;
В)ЧИСЛА ДЛЯ ТОЧКИ;
Г) ПОКАЗНИКИ ТОЧКИ
Г) ПОКАЗНИКИ
ТОЧКИ

13.

ЯК
НАЗИВАЕТЬСЯ
ВІСЬ
ОХ:
ЯК
НАЗИВАЕТЬСЯ
ВІСЬ
ОУ:
А) ОРДИНАТА;
А)АПЛІКАТА;
АПЛІКАТА;
А)
А) ОРДИНАТА;
Б)
Б) ОРДИНАТА;
ОРДИНАТА;
Б) АБСЦИСА;
Б) АБСЦИСА;
АБСЦИСА; ;
В) В)АБСЦИСА
В) БІСЕКТРИСА;
В) БІСЕКТРИСА;
Г)
Г) БІСЕКТРИСА
БІСЕКТРИСА
Г) АПЛІКАТА
Г) АПЛІКАТА
ЯК
НАЗИВАЕТЬСЯ
ВІСЬ
ОZ :
А) АБСЦИСА;
АПЛІКАТА;
Б)Б)АПЛІКАТА;
В)
В) ОРДИНАТА;
ОРДИНАТА;
Г)
Г) БІСЕКТРИСА
БІСЕКТРИСА

14.

ЯКЩО ТОЧКА
НАЛЕЖИТЬ
ОХ,
ОСІ
ТО ЇЇ
КООРДИНАТИ:
ЯКЩО ТОЧКА
НАЛЕЖИТЬ
ОУ
ОСІ
,
ТО ЇЇ
КООРДИНАТИ:
ЯКЩО ТОЧКА
НАЛЕЖИТЬ
ОZ
ОСІ
,
ТО ЇЇ
КООРДИНАТИ:
А) ( О; У; О);
А) ( О; У; О);
А) ( О; У; О);
А)(( О;
О; У;
А)
У; О);
О);
А) ( О; У; О);
Б) (О; О; Z);
Б) (О; О; Z);
Б)
(О; О;
О; Z);
Б) (О;
Z);
Б)
О; Z);
Z);
Б)(О;
(О; О;
В) (Х; О; О);
В) (Х; О; О);
В)(Х;
(Х; О;
В)
О; О);
О);
В) (Х; О; О);

15.

НАЛЕЖАТЬ ПЛОСКОСТІ
НАЛЕЖАТЬ ОСІ ОХ
НАЛЕЖАТЬ ПЛОСКОСТІ
НАЛЕЖАТЬ ПЛОСКОСТІ
ХУ
ХZ
УZ
НАЛЕЖАТЬ ОСІ ОZ
НАЛЕЖАТЬ ОСІ ОУ
ЗНАХОДЯТЬСЯ У ПРОСТОРІ

16.

ХС
ХА
ХВ
A
ХА
С
В
ХВ
ЗНАЙТИ КООРДИНАТИ СЕРЕДИНИ
ВІДРІЗКА: А (2); В (8)
ХС
ХА
ХВ

17.

A
ХВ УВ
ХА УА
у
С
В
ХС УС
о
х
а) Знайдіть координати середини відрізка АВ.
Дані точки: А ( - 1; 7 ) и В ( 7; 1).
ХС
ХА
ХВ
УС
С
УА
УВ

18.

ХА УА Х
ZА
ХС
УС
ZС
А
ХС УС ZС
УА
z
ХХВВУ В Z В
В
УВ
С
A
у
х

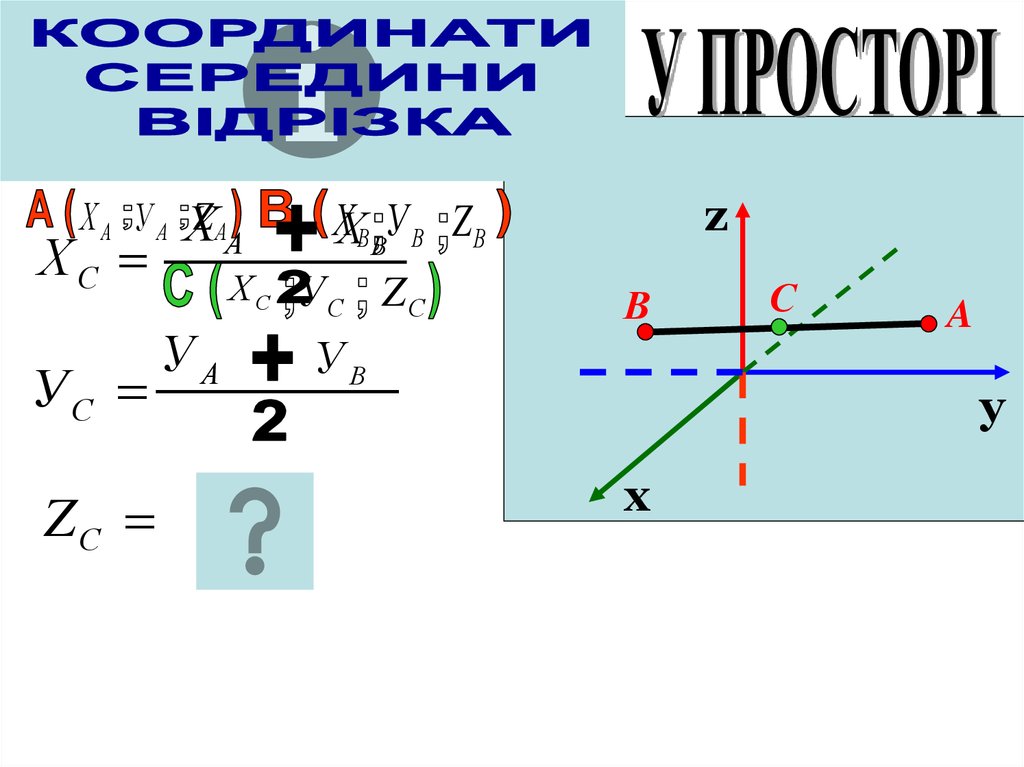
19.

С
z A
С2
КОЖНА КООРДИНАТА
СЕРЕДИНИ ВІДРІЗКА
ДОРІВНЮЄ
В2
ПІВСУМІ
ВІДПОВІДНИХ
КООРДИНАТ ЙОГО
КІНЦІВ
ZС
ZА
ZВ
В
у
А1
х
С1
В1

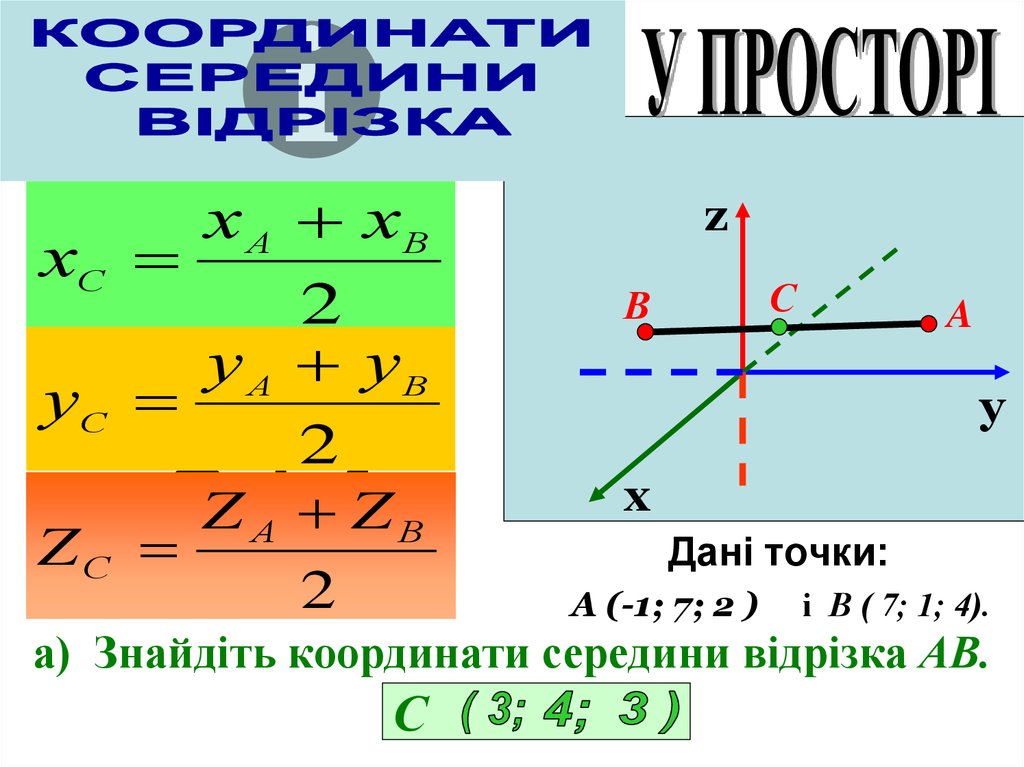
20.

ХхА А ХхВ В
Х
хСС
2
У Ау А
У Ву В
УуСС
2
ZА
ZВ
ZС Z А Z В
ZС
2
z
С
В
A
у
х
Дані точки:
А (-1; 7; 2 )
і В ( 7; 1; 4).
а) Знайдіть координати середини відрізка АВ.
С

21.

у
A
В
Дані точки: А ( - 1; 7 ) та В ( 7; 1).
о
х
Знайти відстань між двома точками
на площині
АВ
АВ
х
хА уВ у А
2
В
2
х7В (-1)
хА
2
|АВ| =
у1В у7А
10
2

22.

В хВ уВ zВ
z
А хА уА z А
КВАДРАТ ВІДСТАНІ
МІЖ ДВОМА ТОЧКАМИ
ДОРІВНЮЄ СУМІ
КВАДРАТІВ РІЗНИЦЬ
ЇХ ВІДПОВІДНИХ
КООРДИНАТ
С
у
А1 хА уА 0
В1 хВ уВ 0
х
АВ = х В х А у В у А ( z B z A ) 2
2
2

23.

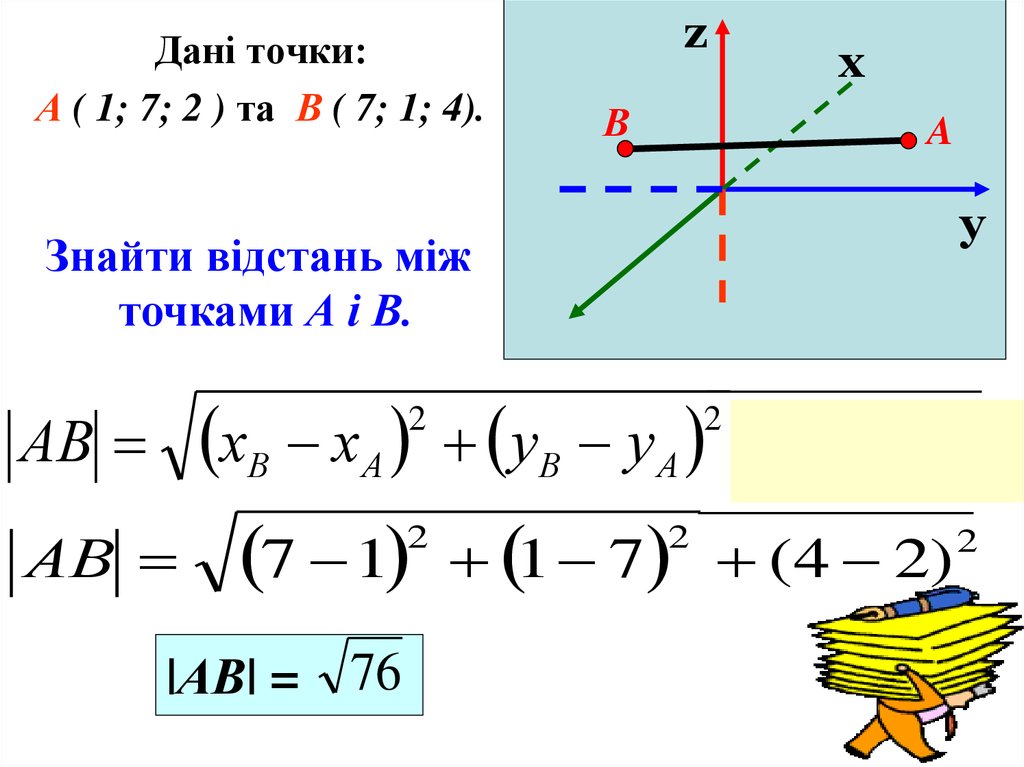
Дані точки:
А ( 1; 7; 2 ) та В ( 7; 1; 4).
z
В
х
A
у
Знайти відстань між
точками А і В.
хВ х А у В у А
АВ
2
АВ
7 1
|АВ| = 76
2
2
( zB z A )
1 7 (4 2)
2
2
2

24.

НА КООРДИНАТНІЙ
ПРЯМІЙ
С
A
х А хВ
хС
2
В
ХА
ХВ
НА КООРДИНАТНІЙ
ПЛОЩИНІ
A
у
С
В
о
z
х
х А хВ
хС
2
ВІДСТАНЬ МІЖ
ДВОМА ТОЧКАМИ
АВ Х В Х А
АВ
у А уВ
уС
2
хВ х А 2 у В у А 2
х А хВ
В хВ уВ zВ хС
2
У ПРОСТОРІ
С Х С ;УС ; ZC
А хА уА z А х
у
КООРДИНАТИ
СЕРЕДИНИ
ВІДРІЗКА
уС
ZС
у А уВ
2
Z А ZВ
2
АВ
хВ х А 2 у В у А 2
(zB z A )2