Приближение функций (глава 3)

1.

Глава 3 ПРИБЛИЖЕНИЕ ФУНКЦИЙ
.
Интерполяция:
y
Дано:
1. Таблица значений функции
2. Значение аргумента «внутри»
таблицы
50
Найти
40
30
20
Найти:
Значение функции при заданном
значении аргумента
Дано
10
0
0
-10
1
2
3
4
5
6
7
8

2.

Глава 3 ПРИБЛИЖЕНИЕ ФУНКЦИЙ
.
Экстраполяция:
y
Дано:
1. Таблица значений функции
2. Значение аргумента «вне»
таблицы
50
40
Найти
30
20
Найти:
Значение функции при заданном
значении аргумента
Дано
10
0
0
-10
1
2
3
4
5
6
7
8

3.

Глава 3 ПРИБЛИЖЕНИЕ ФУНКЦИЙ
.
Аппроксимация:
Дано:
1. Таблица значений функции
2. Вид зависимости для
аппроксимации
y
50
y = 8x - 17
40
30
Найти
20
Найти:
Коэффициенты зависимости
10
0
0
-10
-20
1
2
3
4
5
6
7
8

4.

Глава 3 ПРИБЛИЖЕНИЕ ФУНКЦИЙ
.
Интерполяция:
y
Другая постановка задачи
интерполяции:
50
Узлы
интерполяции
40
Заданы значения функции f(xi) в
узлах интерполяции x1, … xn.
30
20
Найти функцию (x, a1,…an) такую,
чтобы (xi, a1,…an)= f(xi), i=1,…n
10
0
0
-10
1
2
3
4
5
6
7
8

5.

Глава 3 ПРИБЛИЖЕНИЕ ФУНКЦИЙ
.
Интерполяция:
y
Другая постановка задачи
интерполяции:
50
Узлы
интерполяции
40
Заданы значения функции f(xi) в
узлах интерполяции x1, … xn.
30
20
Найти функцию (x, a1,…an) такую,
чтобы (xi, a1,…an)= f(xi), i=1,…n
10
0
0
1
2
3
4
5
6
7
8
-10
Если функция (x, a1,…an) зависит от параметров нелинейно, то интерполяцию
называют нелинейной.
Линейной будем считать такую интерполяцию, когда
i(x) – заданные линейно независимые функции.

6.

Глава 3 ПРИБЛИЖЕНИЕ ФУНКЦИЙ
.
Интерполяция:
y
Другая постановка задачи
интерполяции:
50
Узлы
интерполяции
40
Заданы значения функции f(xi) в
узлах интерполяции x1, … xn.
30
20
Найти функцию (x, a1,…an) такую,
чтобы (xi, a1,…an)= f(xi), i=1,…n
10
0
0
1
2
3
4
5
6
7
8
-10
В такой постановке задача интерполяции легко решается:
k=1,…,n
Коэффициенты аi находят решая систему линейных алгебраических уравнений.

7.

.
Глава 3 ПРИБЛИЖЕНИЕ ФУНКЦИЙ
Интерполяция:
Часто для интерполяции используют многочлены вида:
Ln(x)=a0+ a1x+…+ anxn
(Эти многочлены легко вычислять)
Задача: как найти коэффициенты ai без решения системы уравнений?

8.

Глава 3 ПРИБЛИЖЕНИЕ ФУНКЦИЙ
.
Интерполяция:
Интерполяционный полином Лагранжа :
n
n
(x x )
j
Ln ( x) j 0n; j k
f ( xk )
k 0
( xk x j )
xj, j=0…n - заданные значения аргументов,
f(xj)=fj – соответствующие этим аргументам
значения функции.
j 0; j k
Например, для n=2:
L2 ( x)
( x x0 )( x x2 )
( x x0 )( x x1 )
( x x1 )( x x2 )
f0
f1
f2
( x0 x1 )( x0 x2 )
( x1 x0 )( x1 x2 )
( x2 x0 )( x2 x1 )
a2 x 2 a1 x a0
a2
f0
f1
f2
( x0 x1 )( x0 x2 ) ( x1 x0 )( x1 x2 ) ( x2 x0 )( x2 x1 )
Примечание: При изменении количества узлов интерполяции n все слагаемые
полинома Лагранжа необходимо пересчитывать.

9.

Глава 3 ПРИБЛИЖЕНИЕ ФУНКЦИЙ
.
Интерполяция:
Интерполяционный полином Лагранжа :
Например, для n=2:
L2 ( x)
( x x0 )( x x2 )
( x x0 )( x x1 )
( x x1 )( x x2 )
f0
f1
f2
( x0 x1 )( x0 x2 )
( x1 x0 )( x1 x2 )
( x2 x0 )( x2 x1 )
a2 x 2 a1 x a0
a2
f0
f1
f2
;
( x0 x1 )( x0 x2 ) ( x1 x0 )( x1 x2 ) ( x2 x0 )( x2 x1 )
( x x1 )( x x2 )( x x3 )
L3 ( x)
f 0 ......... b3 x 3 b2 x 2 b1 x b0
( x0 x1 )( x0 x2 )( x0 x3 )
Примечание: При изменении количества узлов интерполяции n все слагаемые
полинома Лагранжа необходимо пересчитывать.

10.

.
Глава 3 ПРИБЛИЖЕНИЕ ФУНКЦИЙ
Интерполяция:
Интерполяционный полином Ньютона:
Разделенные разности первого порядка:
i=0,…(n-1)
Разделенные разности второго порядка:
i=0,…,(n-2)
Аналогично по разделенным разностям (k-1)-го порядка
вычисляем разделенные разности порядка k:
Эта формула удобна для последовательных вычислений в таблице.

11.

Глава 3 ПРИБЛИЖЕНИЕ ФУНКЦИЙ
.
Интерполяция:
Вычисление разностей:
x
Y
f1i
f2i
f3i
X0
f0
f10=(f1-f0)/(x1-x0)
f20=(f11-f10)/(x2-x0) f30=(f21-f20)/(x3-x0)
X1
F1
f11=(f2-f1)/(x2-x1)
f21=(f12-f11)/(x3-x1)
X2
F2
f12=(f3-f2)/(x3-x2)
x3
F3

12.

Глава 3 ПРИБЛИЖЕНИЕ ФУНКЦИЙ
.
Интерполяция:
Вычисление разностей:
x
Y
f1i
f2i
f3i
X0
f0
f10=(f1-f0)/(x1-x0)
f20=(f11-f10)/(x2-x0) f30=(f21-f20)/(x3-x0)
X1
f1
f11=(f2-f1)/(x2-x1)
f21=(f12-f11)/(x3-x1)
X2
f2
f12=(f3-f2)/(x3-x2)
x3
f3
Интерполяционный полином Ньютона:
Интерполяционный многочлен Ньютона является другой формой записи
интерполяционного многочлена Лагранжа.
При увеличении n ранее вычисленные коэффициенты не изменяются.

13.

.
Глава 3 ПРИБЛИЖЕНИЕ ФУНКЦИЙ
Интерполяция:
Погрешность интерполяции:

14.

.
Глава 3 ПРИБЛИЖЕНИЕ ФУНКЦИЙ
Интерполяция:
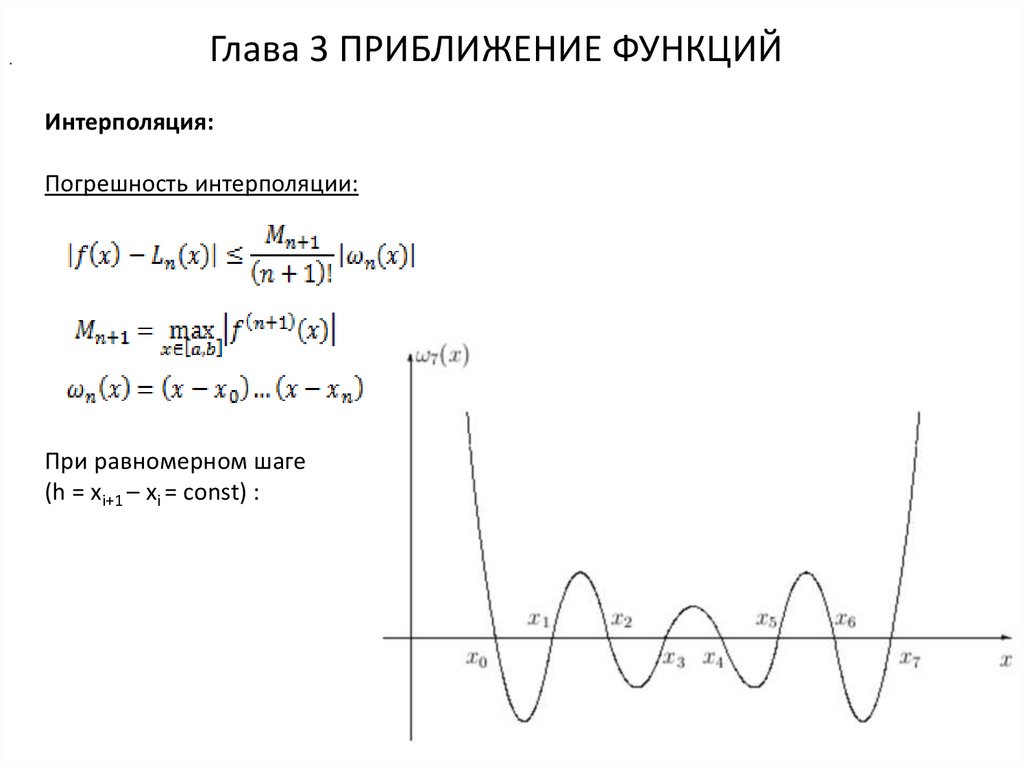
Погрешность интерполяции:
При равномерном шаге
(h = xi+1 – xi = const) :

15.

.
Глава 3 ПРИБЛИЖЕНИЕ ФУНКЦИЙ
Интерполяция:
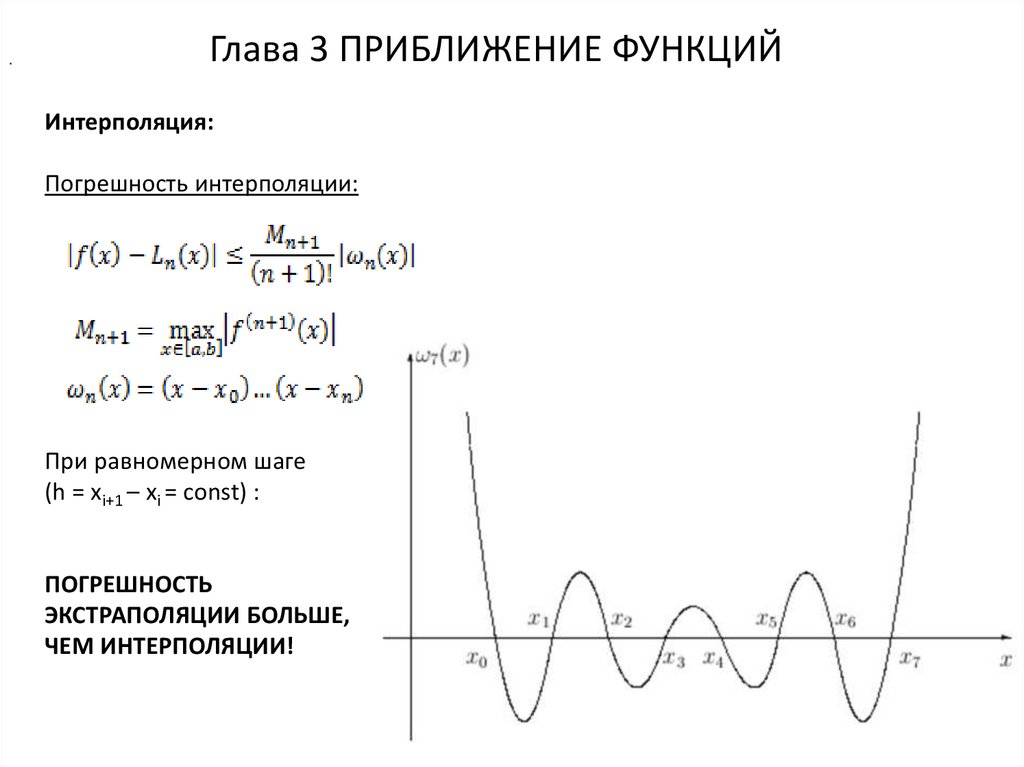
Погрешность интерполяции:
При равномерном шаге
(h = xi+1 – xi = const) :
ПОГРЕШНОСТЬ
ЭКСТРАПОЛЯЦИИ БОЛЬШЕ,
ЧЕМ ИНТЕРПОЛЯЦИИ!

16.

.
Глава 3 ПРИБЛИЖЕНИЕ ФУНКЦИЙ
Интерполяция:
Погрешность интерполяции
Более грубая оценка:
Можно подбирать n и/или h.