Несобственные интегралы с бесконечными пределами интегрирования

1.

ЛЕКЦИЯ
ТЕМА: «НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ С
БЕСКОНЕЧНЫМИ ПРЕДЕЛАМИ
ИНТЕГРИРОВАНИЯ»
«

2.

Давайте вспомним!
первообразных функций
f ( x)dx F ( x) C
2) определённый интеграл – это ч и с л о
(например, площадь криволинейной трапеции)
b
f ( x)dx F ( x) F (b) F (a)
b
a
a
3) Отрезок интегрирования
a; b К О Н Е Ч Е Н
Подынтегральная функция f (x)
2
Н Е П Р Е Р Ы В Н А на отрезке интегрирования
25.02.2023
1) неопределённый интеграл – это м н о ж е с т в о

3.

ПЛАН
25.02.2023
1. Несобственные интегралы I рода
определение
геометрическая интерпретация
вычисление
2. Признаки сходимости несобственных
интегралов I рода
3. Несобственные интегралы II рода
определение
геометрическая интерпретация
вычисление
признаки сходимости
3

4.

НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ I РОДА
b
25.02.2023
Определение 1: несобственным интегралом от
функции f (x) в интервале a,
называется предел интеграла f ( x)dx при b ,
то есть
b
a
f ( x)dx lim f ( x)dx
a
b
a
Если указанный предел существует, то
несобственный интеграл называется
с х о д я щ и м с я , а если не существует, то
расходящимся
4

5.

b
25.02.2023
Определение 2: несобственным интегралом от
функции f (x ) в интервале ( ; b]
называется предел интеграла f ( x)dx при a ,
b
то есть
b
a
f ( x)dx lim f ( x)dx
a
a
Если указанный предел существует, то
несобственный интеграл называется
с х о д я щ и м с я , а если не существует, то
расходящимся
5

6.

Если функция определена и непрерывна на всей
c
c
25.02.2023
числовой прямой, то может существовать
несобственный интеграл данной
функции с двумя бесконечными
пределами интегрирования,
определяющийся формулой:
f ( x)dx f ( x)dx f ( x)dx
где с — произвольное число.
c
b
f ( x)dx lim f ( x)dx lim f ( x)dx
a
a
b
c
6

7.

ЗАМЕЧАНИЕ
25.02.2023
Несобственный
интеграл
I f ( x)dx
называют сходящимся, если
существуют оба предела в
правой части равенства, и
расходящимся, если не
существует хотя бы один из
них
7

8.

НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ (ИЛИ
ИНТЕГРАЛЫ РИМАНА) I РОДА - ЭТО
25.02.2023
ИНТЕГРАЛЫ С БЕСКОНЕЧНЫМИ
ПРЕДЕЛАМИ ИНТЕГРИРОВАНИЯ
I f ( x)dx
a
b
I f ( x)dx
I f ( x) dx
8

9.

В ЫЧИ С ЛЕ Н И Е
НЕ С О Б С ТВ Е ННЫХ И НТЕГРАЛО В
25.02.2023
b
f ( x)dx lim f ( x)dx lim F ( x) lim F (b) F (a)
b
a
b
b
a
b
b
a
b
f ( x)dx lim f ( x)dx lim F ( x) F (b) lim F (a)
b
a
a
a
a
a
b
f ( x)dx lim f ( x)dx lim F ( x) lim F (b) lim F (a)
b
b
a a
b
a
a
b
a
9

10.

ПРИМЕРЫ.
ИССЛЕДОВАТЬ НА СХОДИМОСТЬ ИНТЕГРАЛЫ:
e dx lim e dx lim ( e )
0
x
b
x
0
x
b
b
25.02.2023
1)
b
0
1 1
lim b 0 1
b e e
О т в е т : несобственный интеграл сходится и равен
1(или сходится к 1)
10

11.

2)
dx
lim
ln
x
1 x b
1
25.02.2023
Ответ: несобственный интеграл
стремится к бесконечности или расходится
11

12.

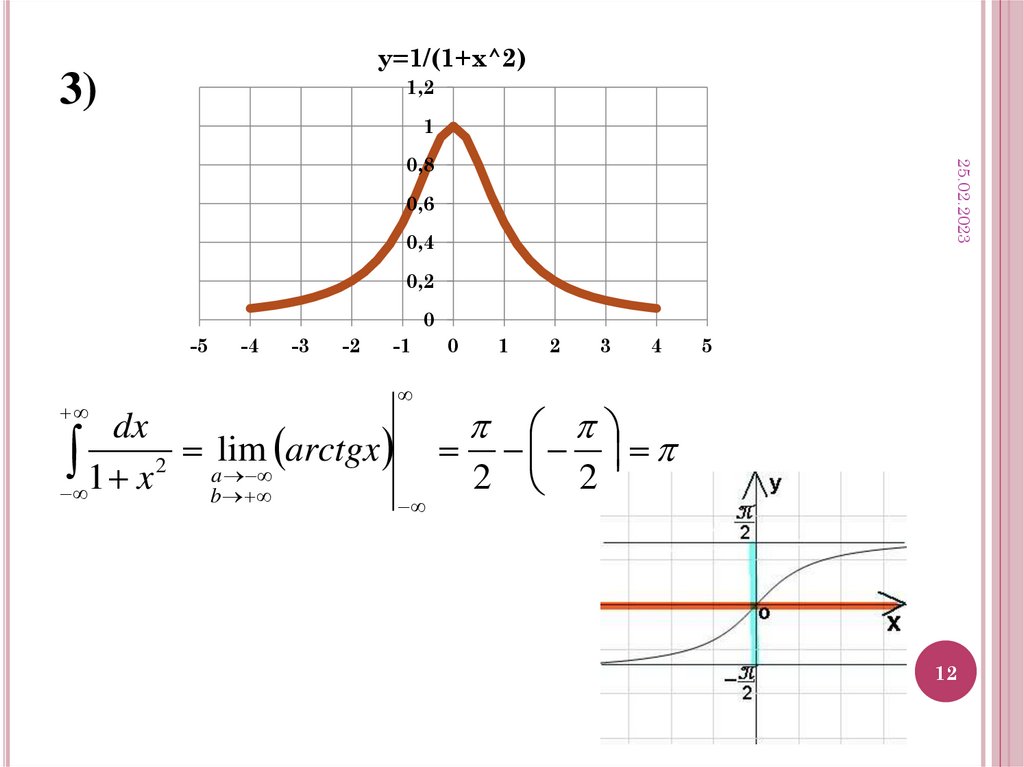
y=1/(1+x^2)
3)
1,2
1
25.02.2023
0,8
0,6
0,4
0,2
0
-5
-4
-3
-2
-1
dx
arctgx
1 x 2 alim
b
0
1
2
3
4
5
2 2
12

13.

Несобственный интеграл выражает
25.02.2023
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
НЕСОБСТВЕННОГО ИНТЕГРАЛА I РОДА
площадь БЕСКОНЕЧНО ДЛИННОЙ
КРИВОЛИНЕЙНОЙ ТРАПЕЦИИ.
b
f ( x)dx lim f ( x)dx
a
b
a
13

14.

25.02.2023
dx
НАПРИМЕР, 2
x
0,5
8
7
6
5
4
3
2
1
0
0
0,5
1
1,5
2
14

15.

ВЫЧИСЛИМ ЭТУ ПЛОЩАДЬ:
b
dx
dx
lim
2
0,5 x b 0 ,5 x 2
25.02.2023
По определению получаем:
1) вычислим интеграл
b
b
0,5
dx
1
1
1
0,5 x 2 x 0,5 x b 2 b
15

16.

25.02.2023
2) Вычислим предел
1
2 2
lim
b
b
dx
Ответ: несобственный интеграл 2 2
x
0,5
т.е. сходится.
Площадь бесконечно длинной
криволинейной трапеции равна 2
16

17.

ПРИЗНАКИ СХОДИМОСТИ
НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ I РОДА
усложняется, если первообразная функция
неизвестна.
В таких случаях иногда удается решить вопрос о
сходимости, используя специальные
25.02.2023
Вопрос о сходимости несобственных интегралов
признаки, которые не требуют знания
первообразной
17

18.

Признак сравнения 1.
Пусть подынтегральная функция f (x ) во всех точках
интервала a, неотрицательна: f ( x ) 0
и для всех значений
выполняется неравенство: 0 f ( x ) ( x )
Тогда:
1)если сходиться интеграл ( x) dx , то сходится и
интеграл
f ( x)dx
a
x
a
2)если расходиться интеграл
интеграл
( x)dx
f ( x)dx , то расходится и
a
a
18

19.

ПРИМЕР
x2
25.02.2023
e dx
Решить вопрос о сходимости интеграла
Решение
x
2
e
dx
x
x
Так как при x 0 e
и
интеграл
e
0
сходится, то сходится и интеграл e dx .
0
Подынтегральная функция чётная, поэтому сходится и
0
интеграл e
x2
x2
dx
Таким образом, заданный интеграл e
x2
dx сходится.
19