Механизмы и уравнения переноса субстанций

1. МЕХАНИЗМЫ И УРАВНЕНИЯ ПЕРЕНОСА СУБСТАНЦИЙ

Основной характеристикой переноса субстанций является поток –
количество субстанции которое переносится за единицу времени
через единицу поверхности.
j
масса
кг/(м2с)
кмоль/(м2с)
энергия
Дж/(м2с) ~ Вт/м2
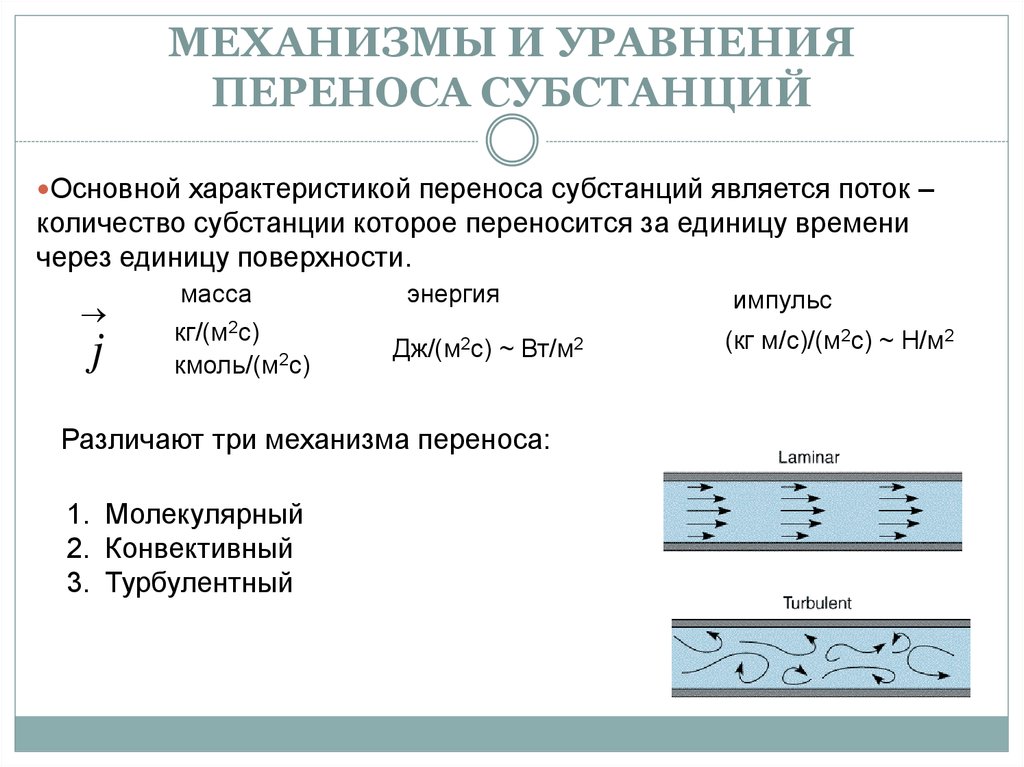
Различают три механизма переноса:
1. Молекулярный
2. Конвективный
3. Турбулентный
импульс
(кг м/с)/(м2с) ~ H/м2

2. Конвективный перенос субстанции

Конвективный механизм переноса субстанции обусловлен движением
макроскопических объемов среды как целого. Движение макроскопических
объемов среды приводит к переносу массы , импульса и энергии
единичного объема
j A A W
q EW
xx Wx wx
yx Wy wx
поток массы
поток энергии
поток импульса
E U Eк Eп

3. Молекулярный перенос субстанции

Переноса субстанции обусловлен тепловым движением молекул
или иных микроскопических частиц (ионов в электролитах и
кристаллах, электронов в металлах).
mmWm2 3
E
kT
2
2
m
k
О2 Т = 273 К
Wm
=461 м/с = 1660 км/ч

4. Молекулярный перенос субстанции (Теплопроводность)

Закон теплопроводности, был впервые сформулирован
Жаном-Батистом Фурье в 1811 г
Перенос тепла
(закон Фурье)
q T a ( cPT )
к п с
- коэффициент теплопроводности, Вт/мК.
а- коэффициент температуропроводности, м2/с.
для газов ~ 10 2 Вт/(м К), для жидкостей ~ 10 1 Вт/(м К), для металлов ~
102 Вт/(м К).

5. Молекулярный перенос субстанции (Перенос импульса)

Закон вязкости Ньютона
wx
( wx )
yx
y
y
где [Па с] и [м2/с] коэффициенты динамической и кинематической
молекулярной вязкости соответственно
В газах ~ 10 5 Па с, в жидкостях ~ 10 3 Па с.

6.

Молекулярный перенос субстанции
(Диффузия)
Перенос массы
Поток меченых частиц в равновесных условиях
ji Di ci
сi[моль/м3]
эйнштейновский коэффициент диффузии
характеризует подвижность молекул
Di
2
i
6 t
Di f ( P,T ,x )

7. Молекулярный перенос субстанции

Перенос массы
Поток массы в неравновесных условиях
cA
K
Д
j A DA
A cA w cA ( wА wK )
RT
cB
K
Д
j B DB
B cB w cB ( wВ wK )
RT
W
А
DА DВ
В
cA A cB B
K
j j A j B c A w cB w cw cW
Д
А
K
W х A w хB w w
Д
А
Д
Д
Д
B
-среднемольная скорость
j cA ( wАД wK W ) c A ( 1 x A )wАД xB wBД
С[моль/м3]
x[мол.дол.]

8.

Среднемольная система координат – суммарный мольный поток вещества = 0
Д
А
j c A ( w w W ) c A ( 1 x A )w xB w DAB
Д
А
K
Д
А
Д
B
cB
j DBA
B
RT
j DAB
Д
A
Д
A
Д
B
DAB xB DA xA DB
Д
B
j j 0
c A A
x A DAB c x A DAB c A
RT x A
cA
A
RT
DBA DAB
- первый закон Фика
ln( A )
DAB DAB 1 x A
x
A
K
WM X Aw X B w w
Д
Д
K
WV Aw B w w
Д
Д
Другие системы координат
-среднемассовая скорость
X [масс.дол]
-среднеобъемная скорость
[объемн.дол]

9. Турбулентный перенос субстанции

j A DТ cA
q т T
wx
wx
yx т
т
y
y
Коэффициенты турбулентного переноса в отличие от молекулярного зависят
главным образом от режима движения среды и в меньшей степени от ее
свойств и параметров состояния

10. Уравнения переноса субстанций

Энергия
Масса
Молекулярный механизм
q a ( cPT )
j DAB cA
Д
A
Импульс
( wx )
yx
y
Конвективный механизм
q EW
j A A W
yx Wy wx
Турбулентный механизм
q т T
j A DТ cA
( wx )
yx т
y

11. ЗАКОНЫ СОХРАНЕНИЯ

Законы сохранения это физические закономерности согласно
которым значения некоторых физических величин должны
оставаться постоянными в любых процессах
При анализе технологических процессов и расчете аппаратов
используются законы сохранения массы, импульса и энергии

12. ЗАКОН СОХРАНЕНИЯ МАССЫ

Интегральная форма закона сохранения массы (уравнения материального
баланса)
M V M вх M вых
dM
d
V
Gвх Gвых
dt
dt
M i V i M i,вх M i,вых
Для непрерывных процессов
Для компонента i
dM i
d i
V
xi вхGвх xi выхGвых
dt
dt
dM i
d
V i xi вхGвх xi выхGвых rV
i
dt
dt
n
r 0
i 1
i
При протекании хим. реакций

13. Локальная форма закона сохранения массы (уравнение неразрывности)

j W
Gx ,вх jx dydz
dV dxdydz
j
Gx ,вых jx dx dydz jx x dx dydz
x
j
j
Gx ,вх Gx ,вых jx jx x dx dydz x dxdydz
x
x
Gy ,вх Gy ,вых
Gz ,вх Gz ,вых
Gвх Gвых
jx j y jz
dV dV
x y z
t
j y
y
dxdydz
jz
dxdydz
z
div j ( W )
t

14. Локальная форма закона сохранения массы (уравнение неразрывности)

( W ) W ( ) (W )
t
const
f ( ,x, y,z )
субстанциональная производная
d dx dy dz
dt t x dt y dt z dt
Wx Wy Wz
W ( )
t x
y
z
t
d
(W ) = 0
dt
wx wy wz
0
x
y
z

15.

cA
jA dS ( jA djA )dS jA 12dF rA dV
dV
cA jA
dF
jA 12
r
x
dV
cA
( jA ) R A
j A ( DAB DТ ) c A c A w

16.

Дифференциальное уравнение конвективной диффузии
c A
c A
c A
c A
wx
wy
wz
( DAB DТ
x
y
z
2c A 2c A 2c A
) 2 2 2 R
y
z
x
dcA
( DAB DТ ) 2 ( c A ) R
d
Решением этого уравнения является поле концентраций
c A f ( ,x, y,z )
НУЖНО ЗАДАТЬ
Условия однозначности:
cA0 f ( 0 ,x, y,z ) начальные условия
cAГР f ( ,xГР , y ГР ,z ГР ) граничные условия
поле скоростей
w f ( x, y,z )

17.

Локальная форма закона сохранения массы
(уравнение неразрывности)
d( m )
0
d
d( dV )
d( )
d( dV )
dV
0
d
d
d
d( dV ) d( dxdydz )
dwx dydz dwy dxdz dwz dxdy
d
d
wx wy wz
dV
dVdiv( w )
y
z
x

18.

f ( ,x, y,z )
субстанциональная производная
d
wx
wy
wz
w ( )
d
x
y
z
w ( ) div( w ) 0
const
wx wy wz
0
x
y
z