Похожие презентации:
Нобелевская премия за открытия в области ядерной модели оболочек
1.
1963 г.Г. Йенсен, М. Гепперт-Майер
Нобелевская премия за открытия в области ядерной модели оболочек
2.
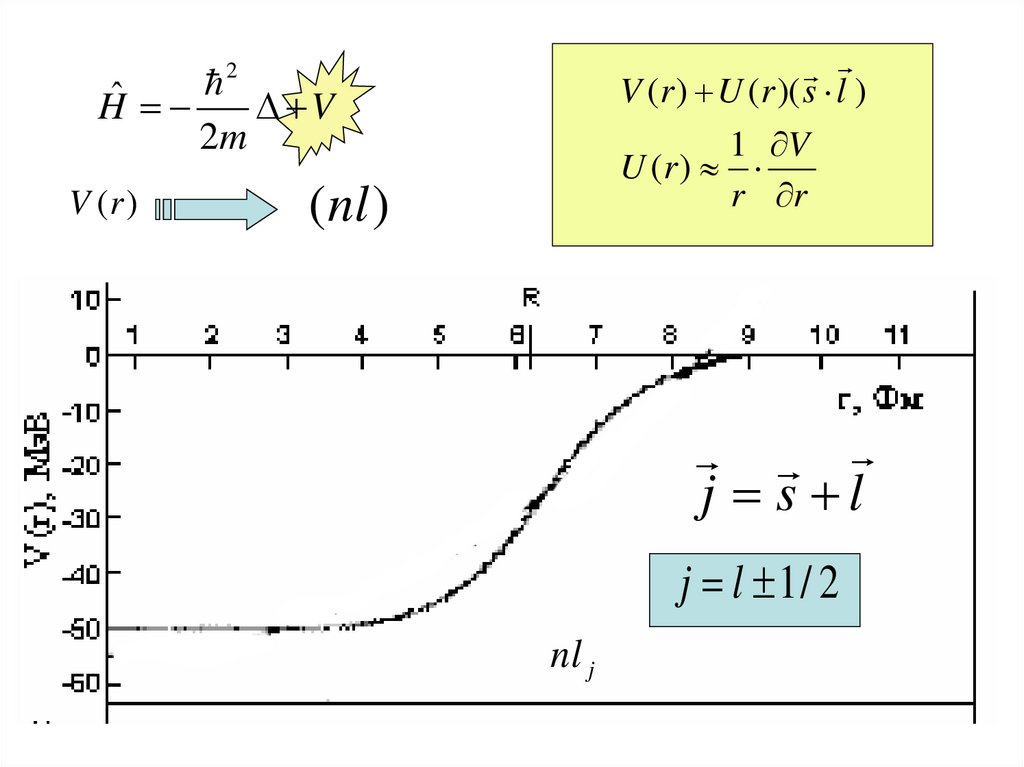
V (r ) U (r )( s l )1 V
U (r )
r r
2
ˆ
H
V
2m
V (r )
(nl )
j s l
j l 1/ 2
nl j
3.
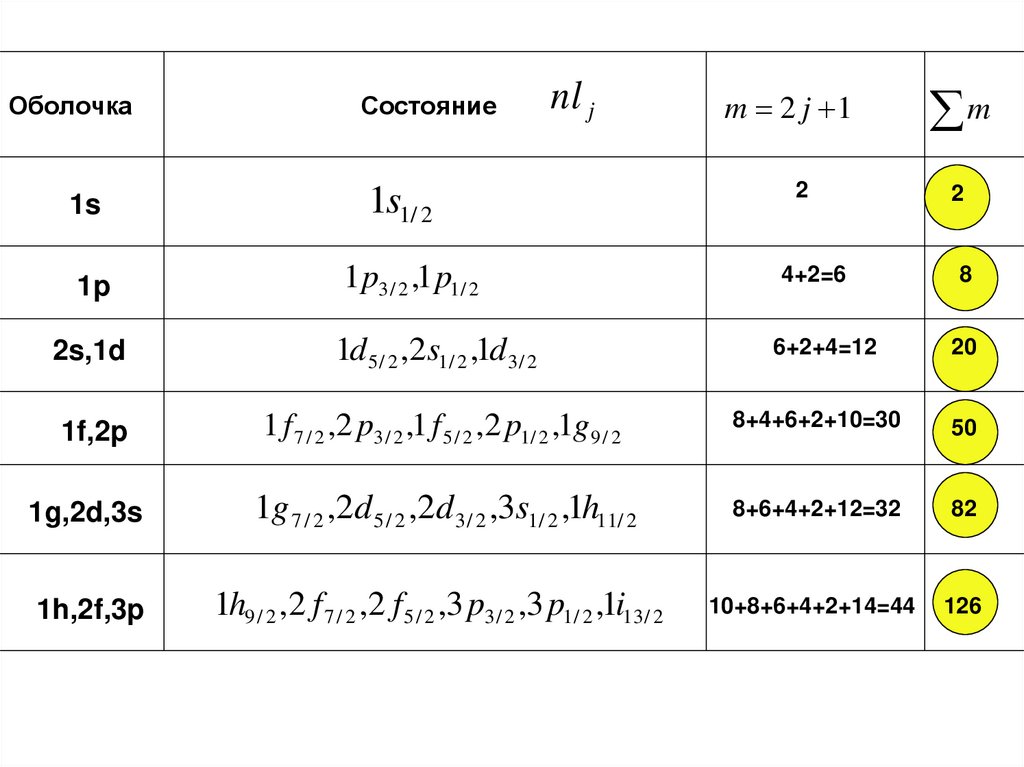
ОболочкаСостояние
nl j
m 2 j 1
m
1s
1s1/ 2
2
2
1p
1 p3 / 2 ,1 p1/ 2
4+2=6
8
2s,1d
1d5 / 2 ,2s1/ 2 ,1d3 / 2
6+2+4=12
20
1f,2p
1 f 7 / 2 ,2 p3 / 2 ,1 f 5 / 2 ,2 p1/ 2 ,1g 9 / 2
8+4+6+2+10=30
50
1g,2d,3s
1g 7 / 2 ,2d 5 / 2 ,2d 3 / 2 ,3s1/ 2 ,1h11/ 2
8+6+4+2+12=32
82
1h,2f,3p
1h9 / 2 ,2 f 7 / 2 ,2 f 5 / 2 ,3 p3 / 2 ,3 p1/ 2 ,1i13/ 2
10+8+6+4+2+14=44
126
4.
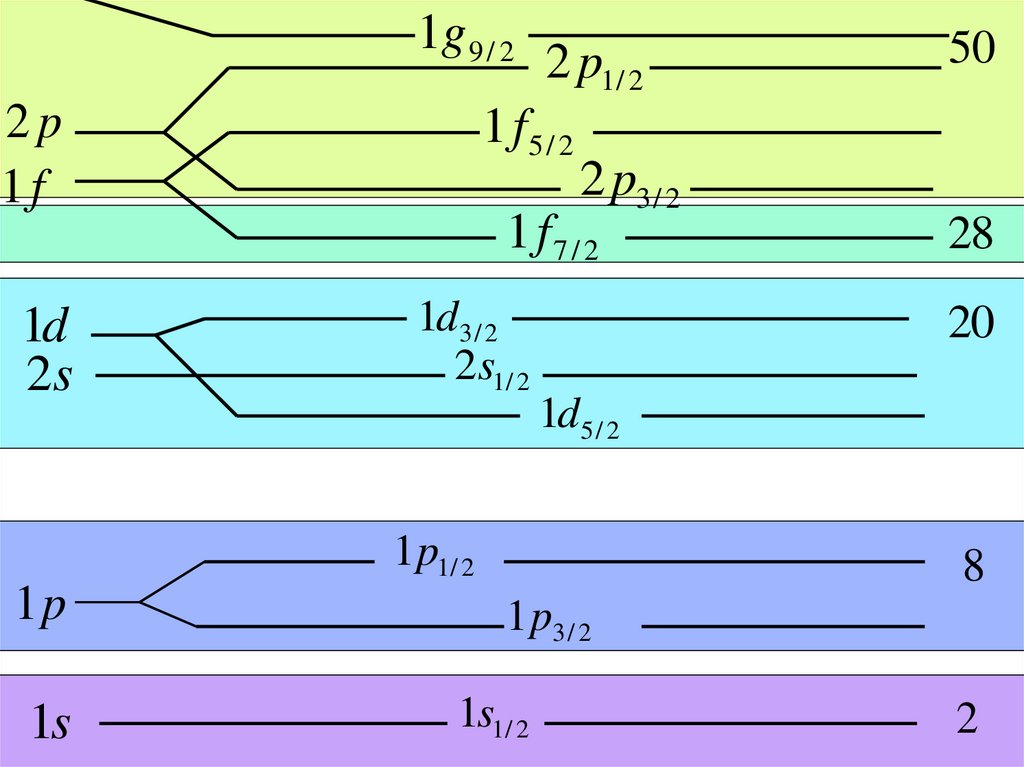
1g 9 / 22p
1f
2 p1/ 2
1 f5 / 2
2 p3 / 2
1 f7 / 2
1d
2s
1d3 / 2
2s1/ 2
1s
28
20
1d5 / 2
1p1/ 2
1p
50
8
1p3 / 2
1s1/ 2
2
5.
6.
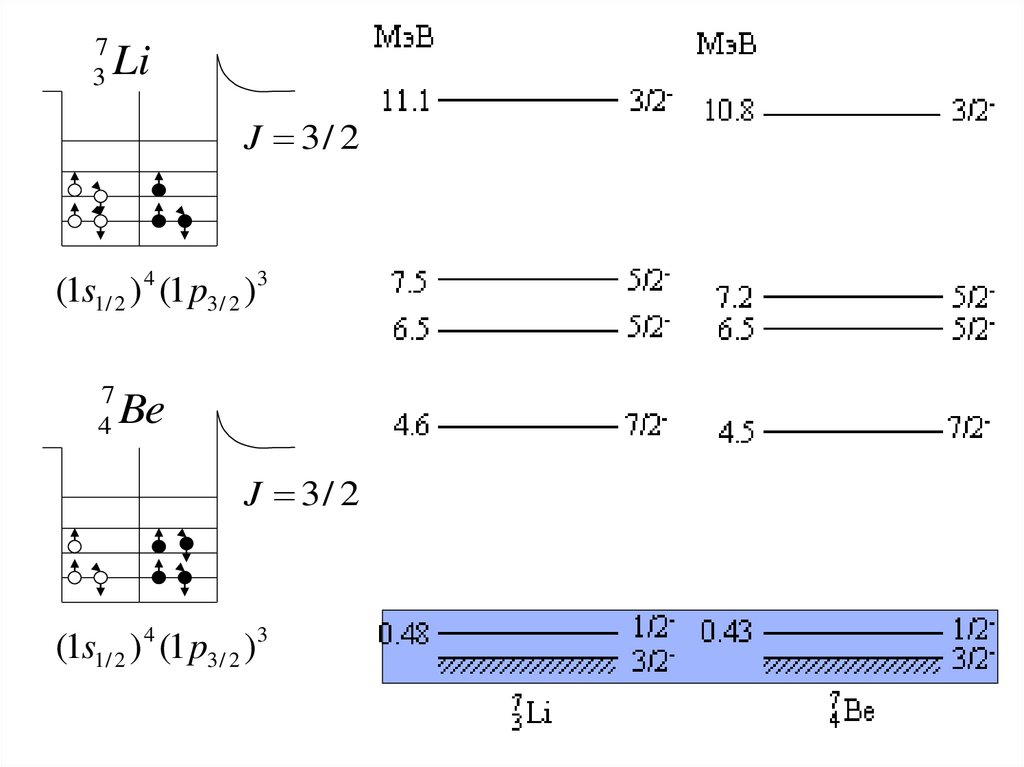
Суммарный момент системы, состоящей из четного числа протонови четного числа нейтронов, равен нулю.
Суммарный момент системы, состоящей из нечетного числа нуклонов,
определяется моментом непарного нуклона.
Суммарный момент нечетно-нечетной системы, непарные нуклоны
которой находятся в одинаковых состояниях, равен удвоенному
моменту нуклона.
7.
73
Li
J 3/ 2
(1s1/ 2 ) 4 (1 p3 / 2 ) 3
7
4
Be
J 3/ 2
(1s1/ 2 ) 4 (1 p3 / 2 ) 3
8.
9.
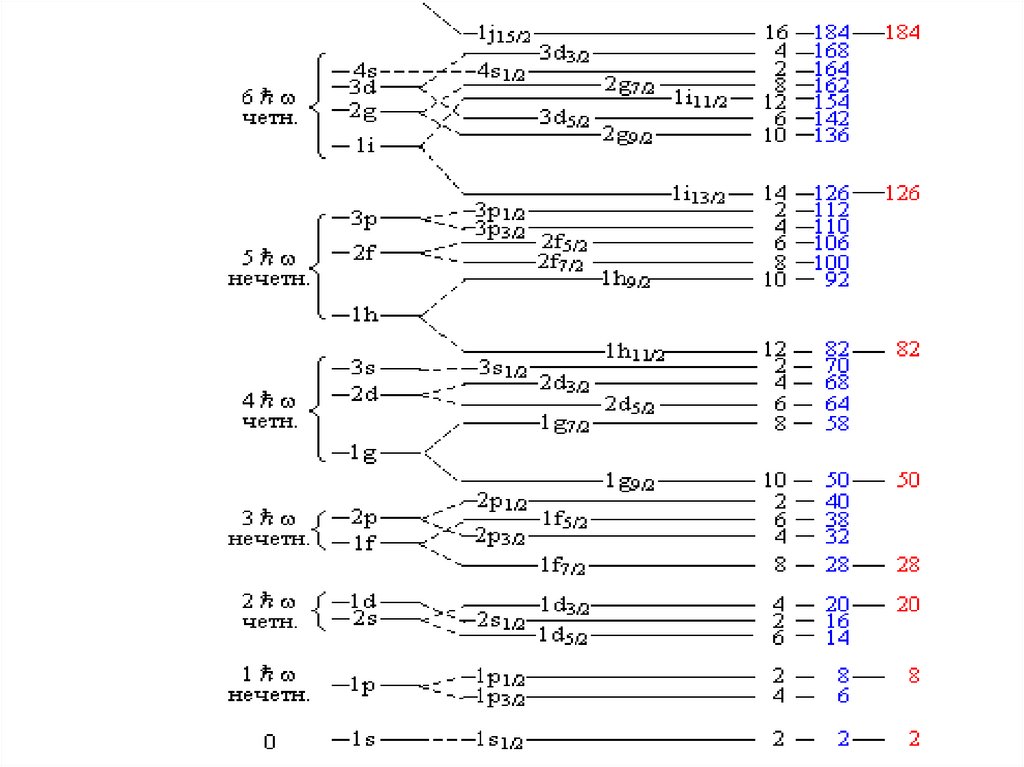
Область применения оболочечной моделимагические числа
для основного и слабовозбужденных
J , P, T , , Q состояний сферических ядер
асимметрия деления ядер
существование ядер изомер
правила отбора при распаде
Недостатки оболочечной модели
несферические ядра
характеристики высоко возбужденных состояний ядер
10.
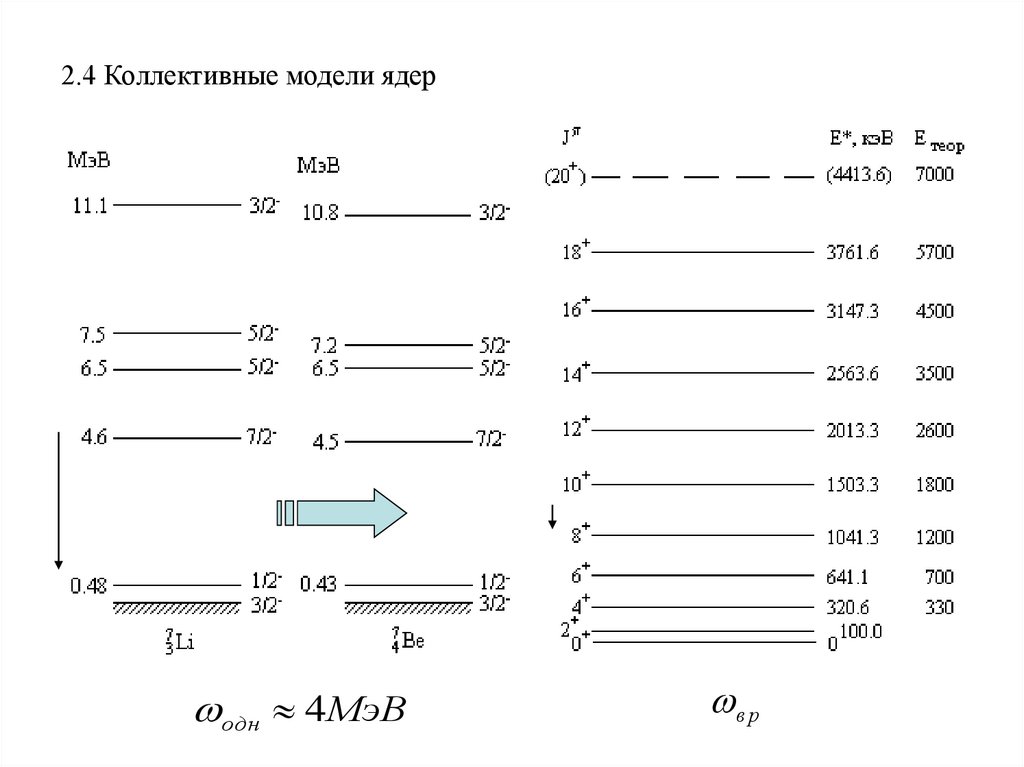
2.4 Коллективные модели ядеродн 4МэВ
в р
11.
12.
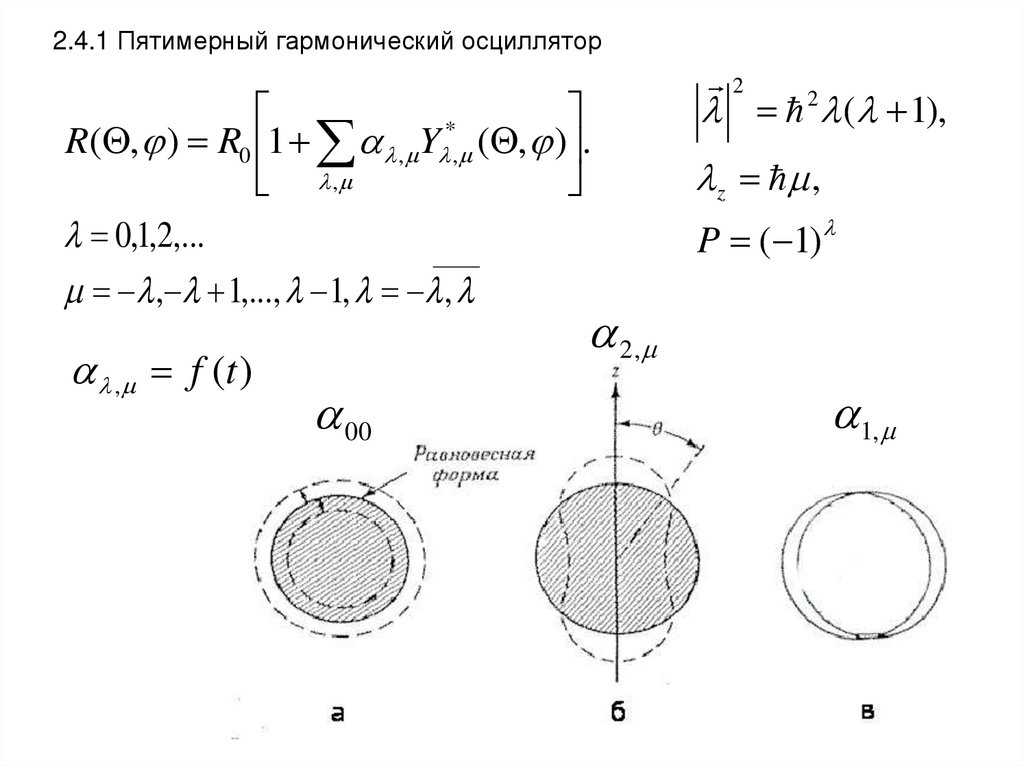
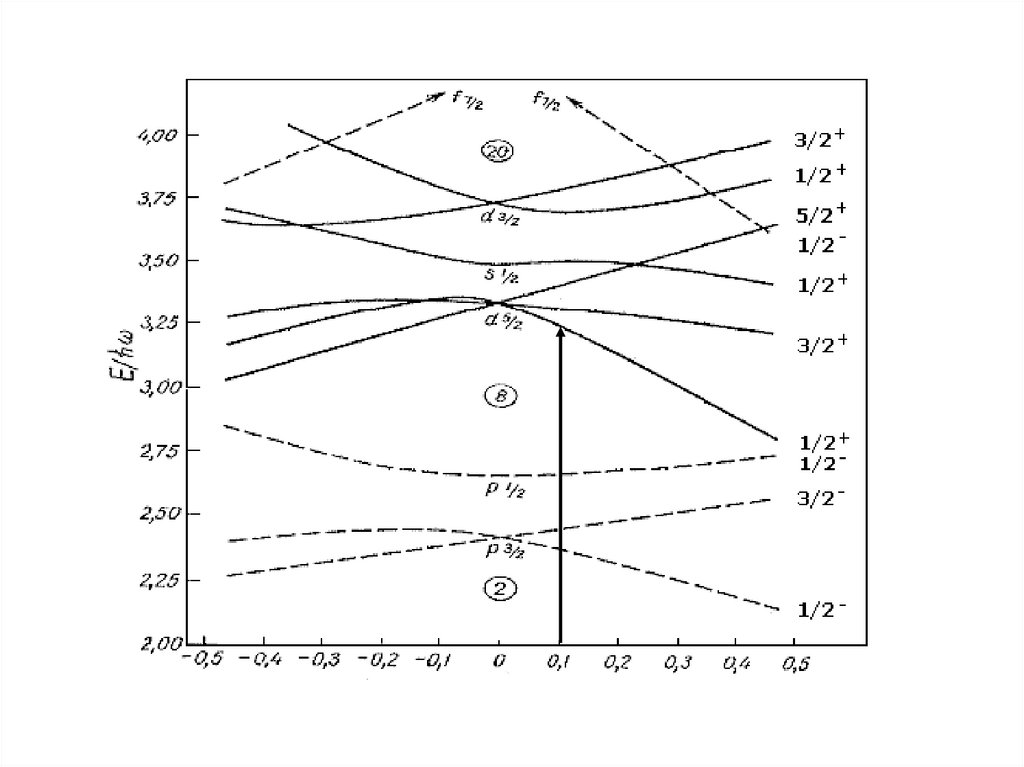
2.4.1 Пятимерный гармонический осциллятор*
R( , ) R0 1 , Y , ( , ) .
,
0,1,2,...
, 1,..., 1, ,
, f (t )
2
2 ( 1),
z ,
P ( 1)
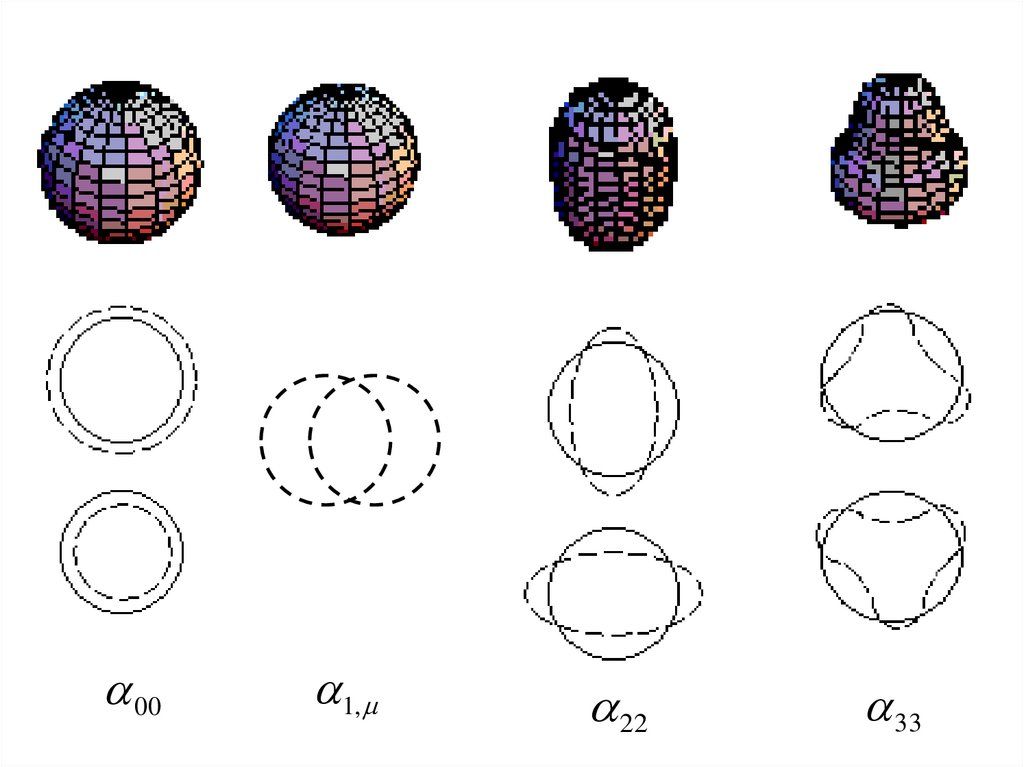
2,
00
1,
13.
001,
22
33
14.
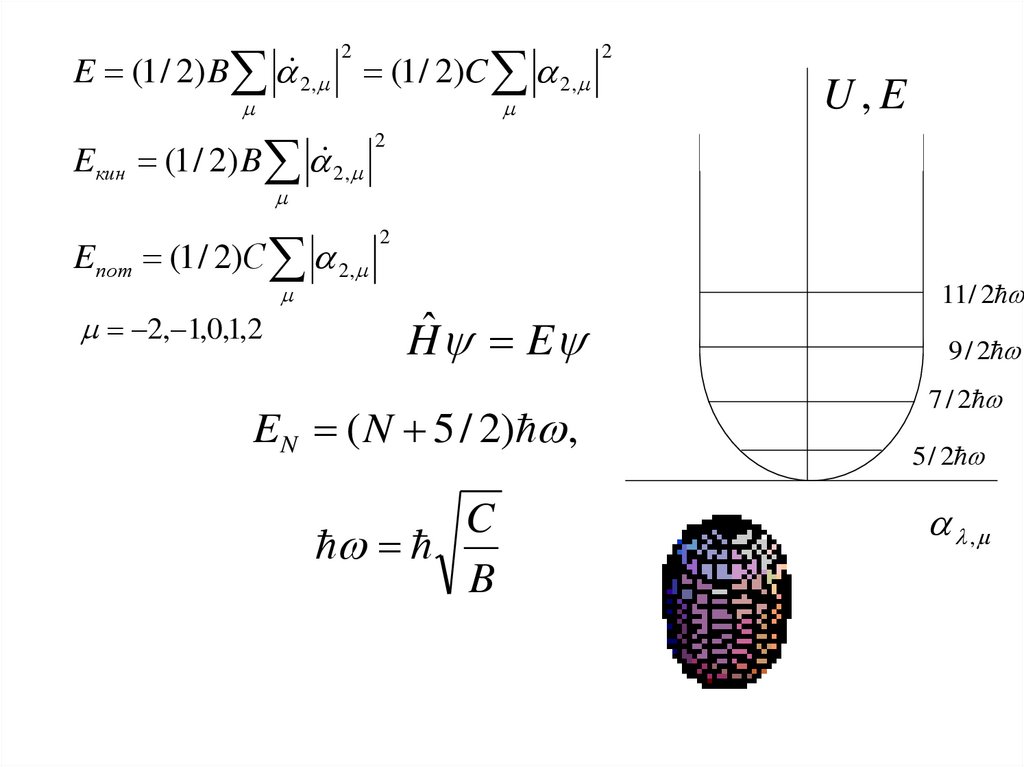
E (1 / 2) B 2, (1 / 2)C 2,2
Eкин (1 / 2) B 2,
2
Eпот (1 / 2)С 2,
2
2
U,E
2, 1,0,1,2
Hˆ E
EN ( N 5 / 2) ,
C
B
11/ 2
9 / 2
7 / 2
5 / 2
,
15.
N 3, E 30 ,2 ,4 ,6
N 2, E 2
0 ,2 ,4
N 1, E
2
N 0, E 0
0
N
j P P
E
16.
N 2N 1
N 0
17.
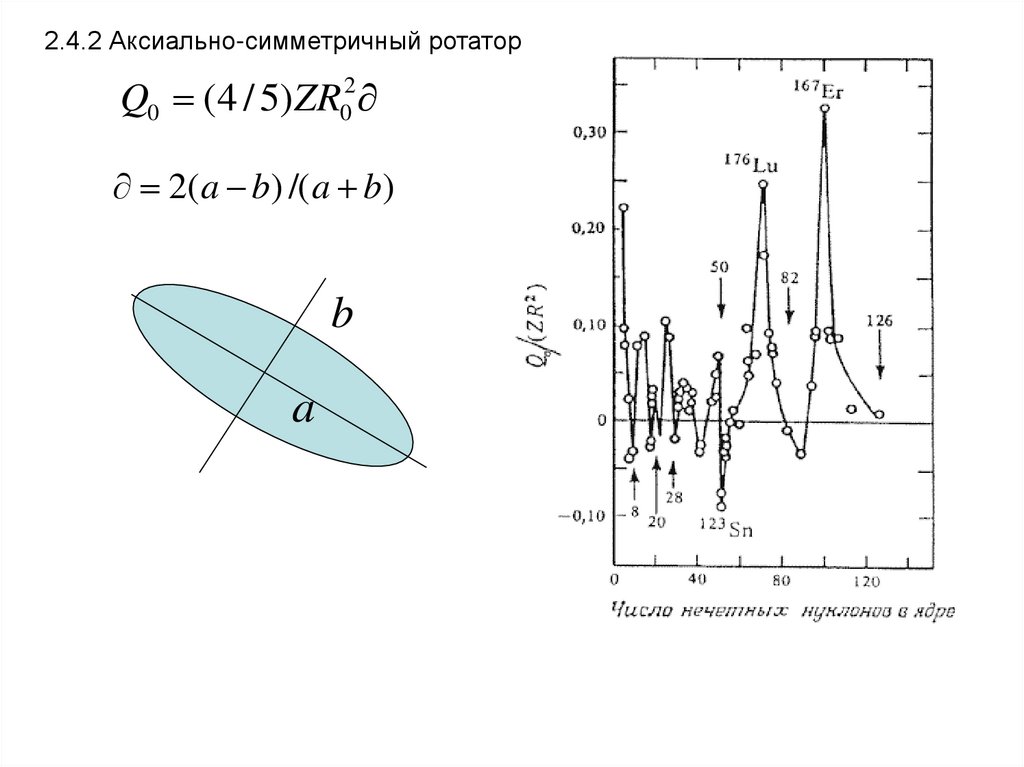
2.4.2 Аксиально-симметричный ротаторQ0 (4 / 5) ZR02
2(a b) /( a b)
b
a
18.
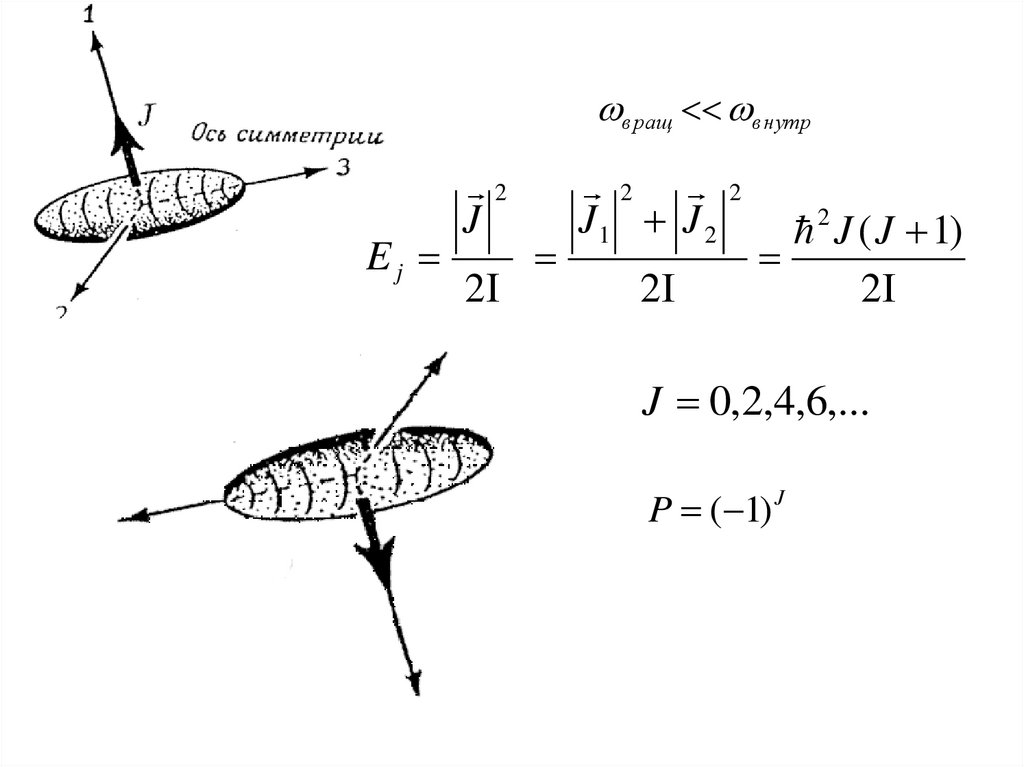
вращ внутрEj
2
J
2
2 2
J1 J 2
2
2 J ( J 1)
2
J 0,2,4,6,...
P ( 1) J
19.
гидр 3Bгидр2
тв AmR02
,
Момент инерции ядра, создаваемый
волной деформации несжимаемой
ядерной жидкости
Момент инерции твердого элипсоида
2
Статическая деформация
Bгидр 3 AmR /(8 )
2
0
Массовый параметр квадрупольной
моды безвихревого течения жидкости
20.
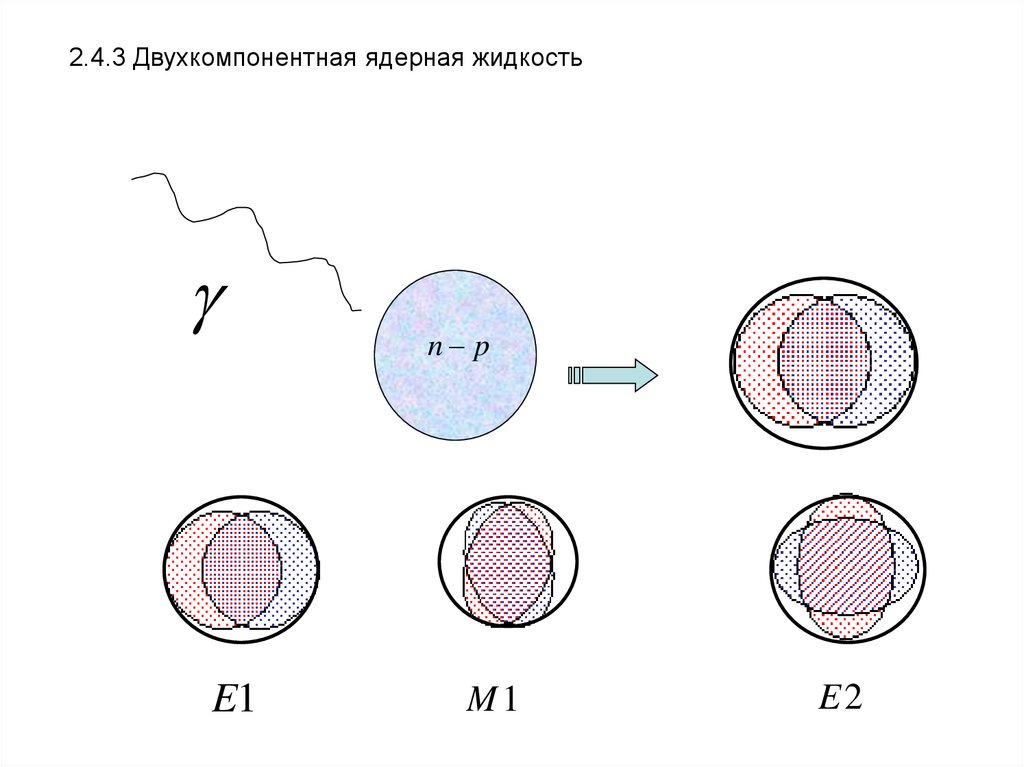
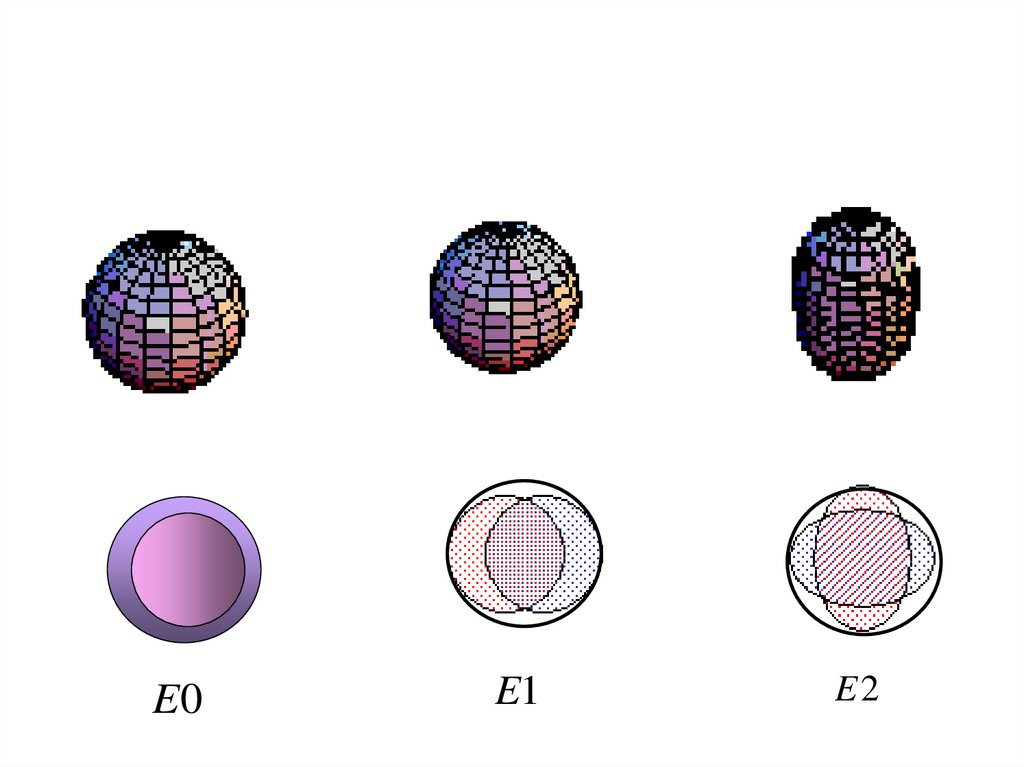
2.4.3 Двухкомпонентная ядерная жидкостьE1
n p
M1
E2
21.
E0E1
E2
22.
(r , t ) p (r , t ) n (r , t ) 0 const1 p (r , t )
p (r , t ) 2
uпол
t 2
2
p (r, t ) p (r ) ei t
Нейтронно-протонные поляризационные
колебания
p (r ) k 2 p (r ) 0
E
k
uпол uпол
2
bпол
u пол
,
m
W A A
2/3
Z2
(2Z A) 2
1/ 3
A 3 / 4
A
A
bпол / 2
23.
p (r )r
r R
0
p (r ) const j (k n, , r ) Y , ( , ),
0,1,2,...
, 1,..., 1, ,
En , uпол хn , / R
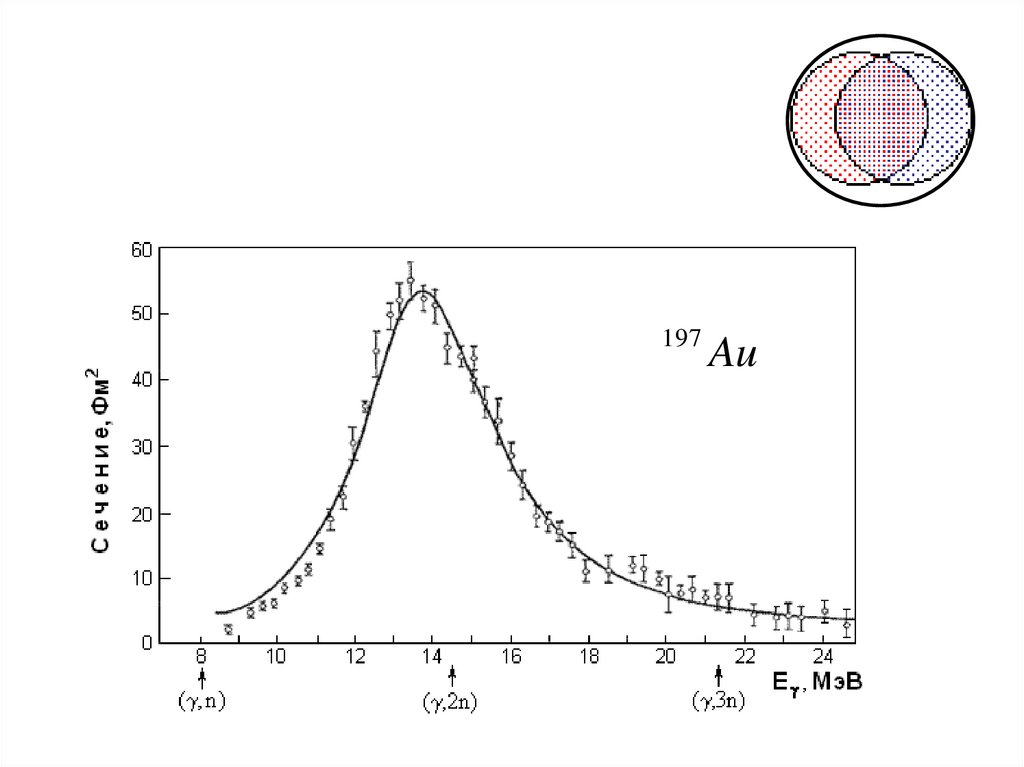
79 A 1/ 3 МэВ.
127 А 1/ 3 МэВ,
170 А 1/ 3 МэВ,
1
2
0
24.
197Au
25.
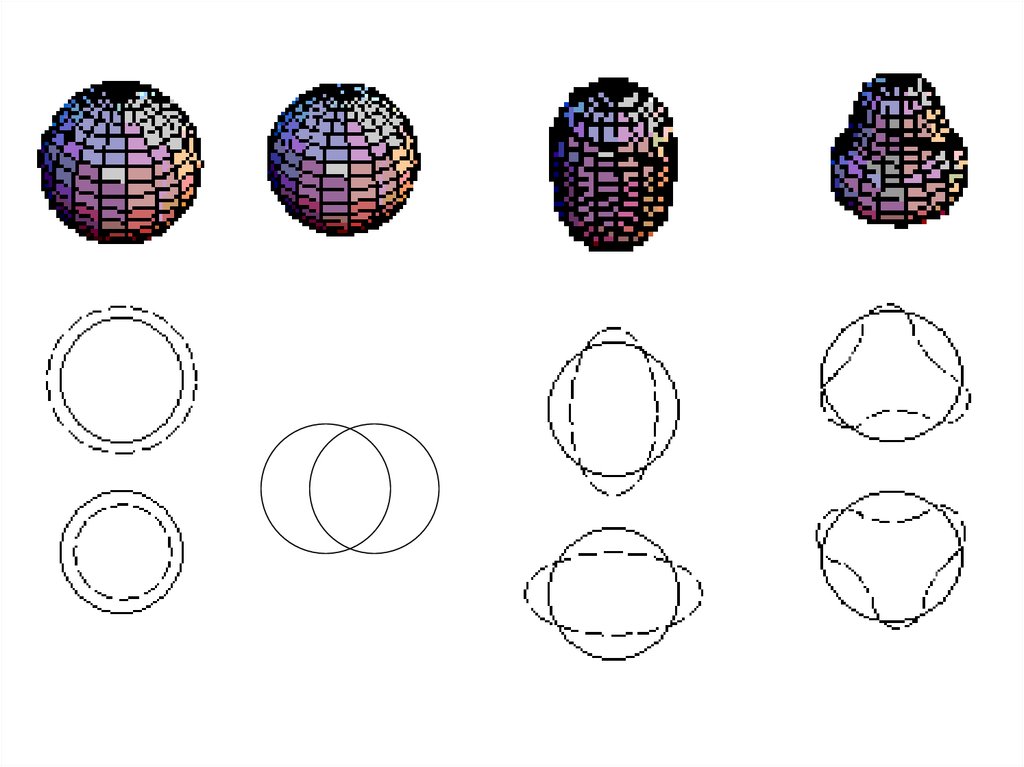
2.5 Обобщенная модель ядраОсновные положения
Сильная связь внешних, по отношению к заполненным оболочкам,
нуклонов с поверхностью остова, в результате чего возникает устойчивая
равновесная деформация ядра. Деформированное ядро имеет форму
эллипсоида вращения.
Выполняется условия адиабатичности (медленности) вращения
деформированного ядра по отношению к характерным скоростям
внутреннего движения: вращ<< внутр.
Возможность приближенного описания движения нуклонов во внутренней,
вращающейся системе координат в рамках одночастичной оболочечной
модели путем введения деформированной потенциальной ямы.
26.
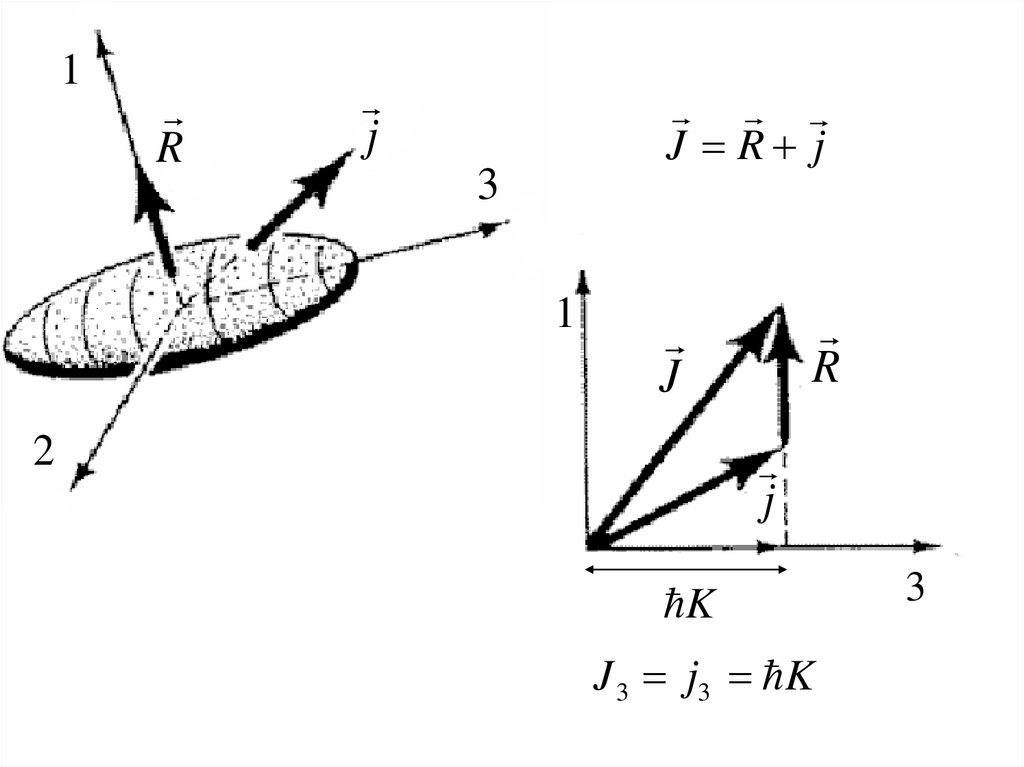
1R
j
J R j
3
1
R
J
2
j
K
J 3 j3 K
3
27.
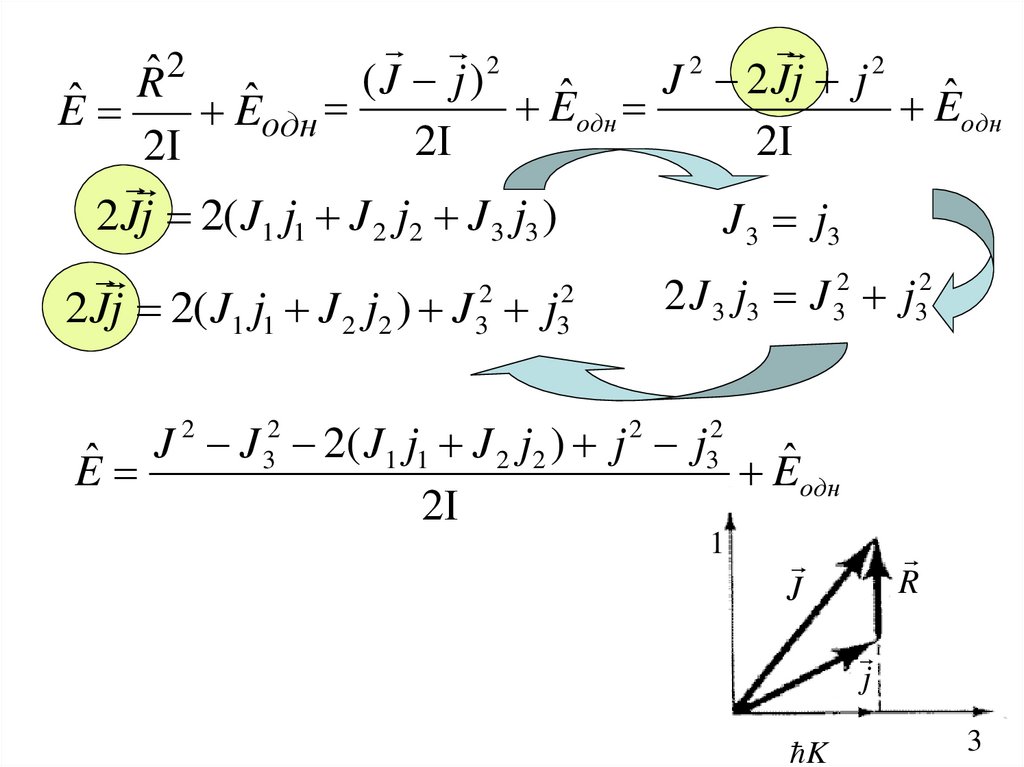
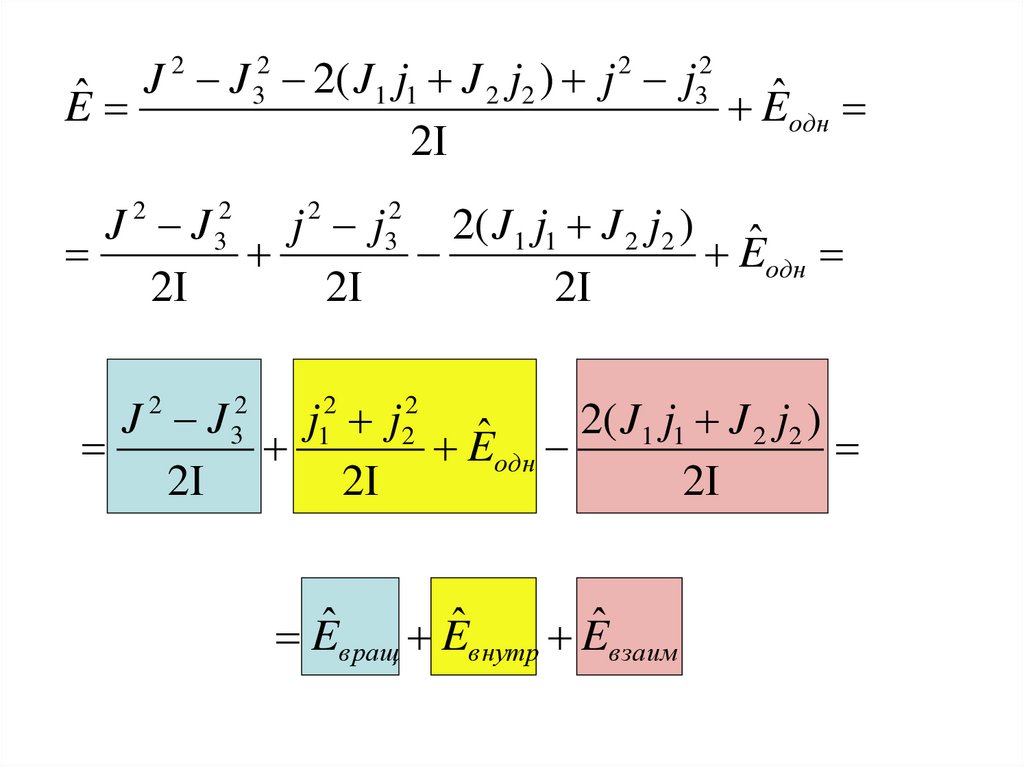
22
2
2
ˆ
(
J
j
)
J
2
J
j
j
R
ˆ
Eодн
Eˆ одн
Eˆ
Eˆ одн
2
2
2
2 Jj 2( J1 j1 J 2 j2 J 3 j3 )
J 3 j3
2
2
2
2
2
J
j
J
j
3 3
3
3
2 Jj 2( J1 j1 J 2 j2 ) J 3 j3
J J 2( J1 j1 J 2 j2 ) j j
ˆ
E
Eˆ одн
2
2
2
3
2
2
3
1
R
J
j
K
3
28.
22
2
2
J
J
2
(
J
j
J
j
)
j
j
3
1 1
2 2
3
Eˆ
Eˆ одн
2
J J
j j
2( J1 j1 J 2 j2 ) ˆ
Eодн
2
2
2
2
2
3
2
2
3
J J
j j
2( J1 j1 J 2 j2 )
ˆ
Eодн
2
2
2
2
2
3
2
1
2
2
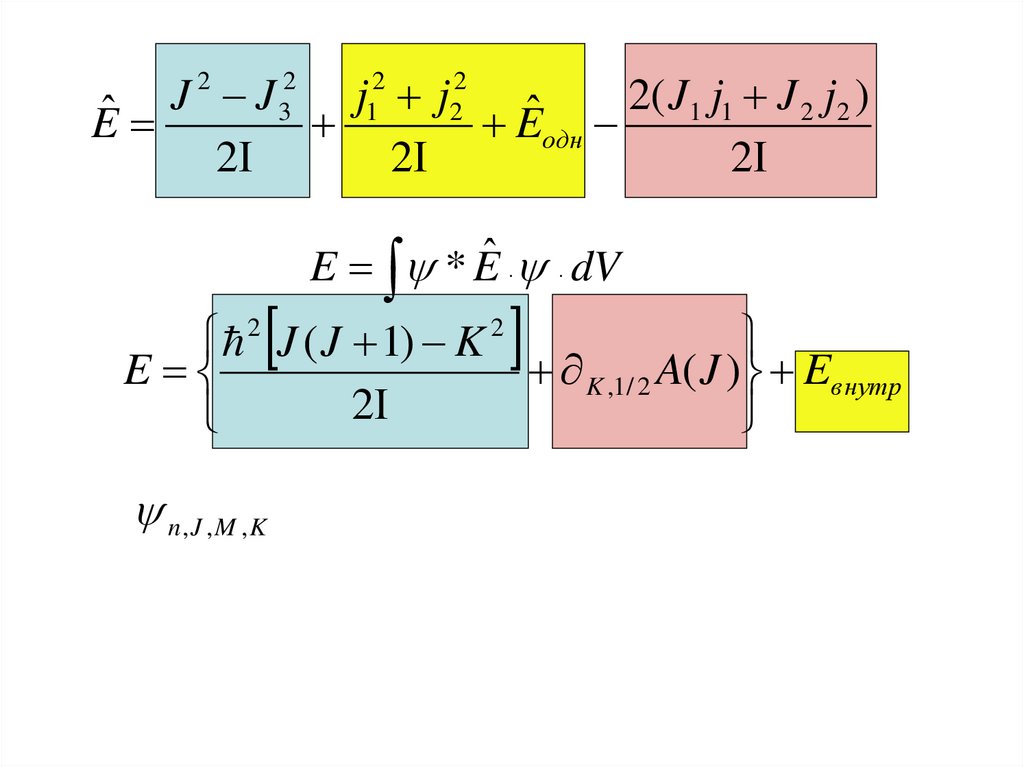
Eˆ вращ Eˆ внутр Eˆ взаим
29.
J Jj j
2( J1 j1 J 2 j2 )
ˆ
ˆ
E
Eодн
2
2
2
2
2
3
2
1
2
2
E * Eˆ dV
2 J ( J 1) K 2
E
K ,1/ 2 A( J ) Eвнутр
2
n, J ,M ,K
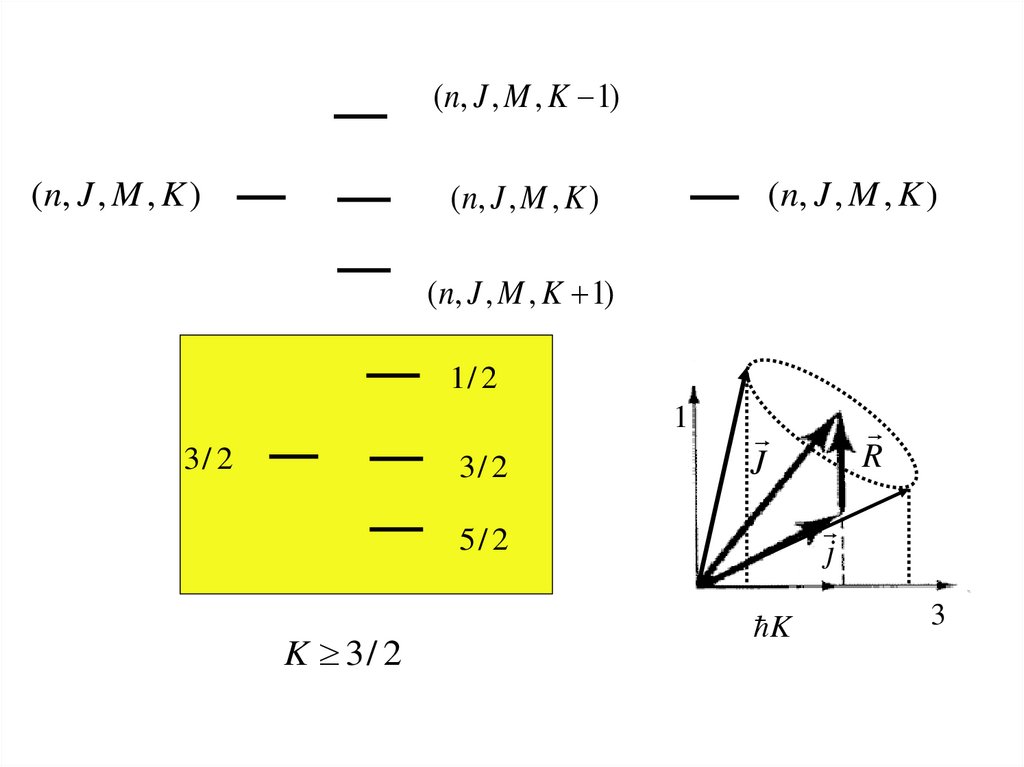
30.
(n, J , M , K 1)(n, J , M , K )
(n, J , M , K )
(n, J , M , K )
(n, J , M , K 1)
1/ 2
1
3/ 2
3/ 2
j
5/ 2
K 3/ 2
R
J
K
3
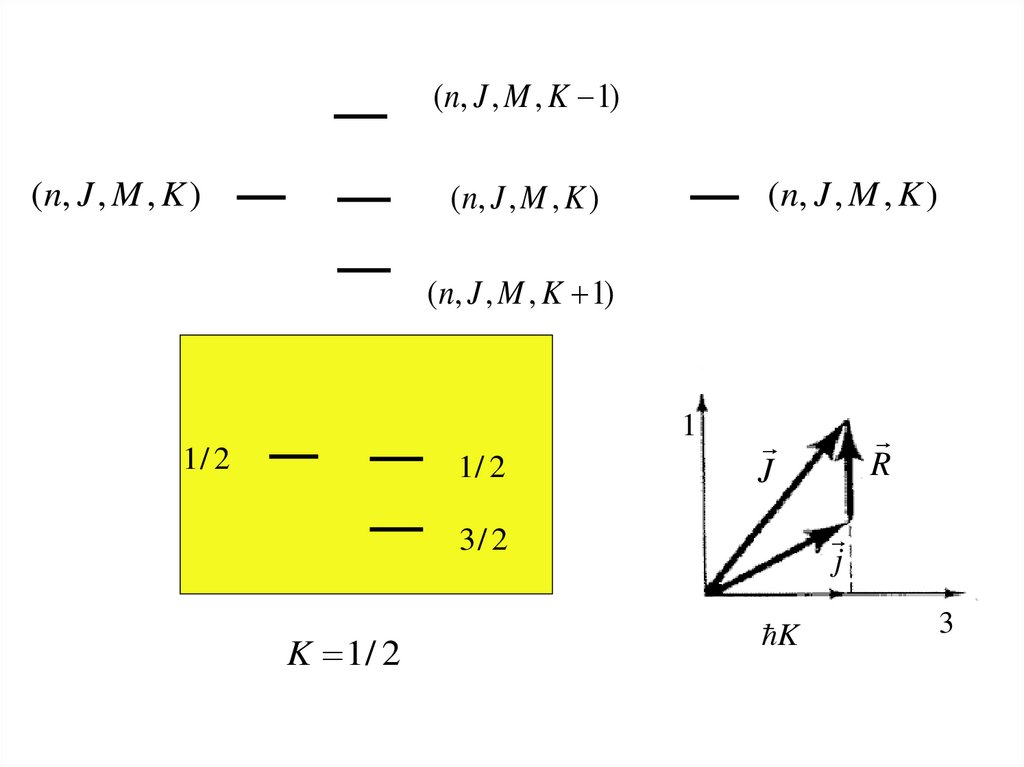
31.
(n, J , M , K 1)(n, J , M , K )
(n, J , M , K )
(n, J , M , K )
(n, J , M , K 1)
1
1/ 2
1/ 2
j
3/ 2
K 1/ 2
R
J
K
3
32.
2 J ( J 1) K 2E
K ,1/ 2 A( J ) Eвнутр
2
249
Bk
33.
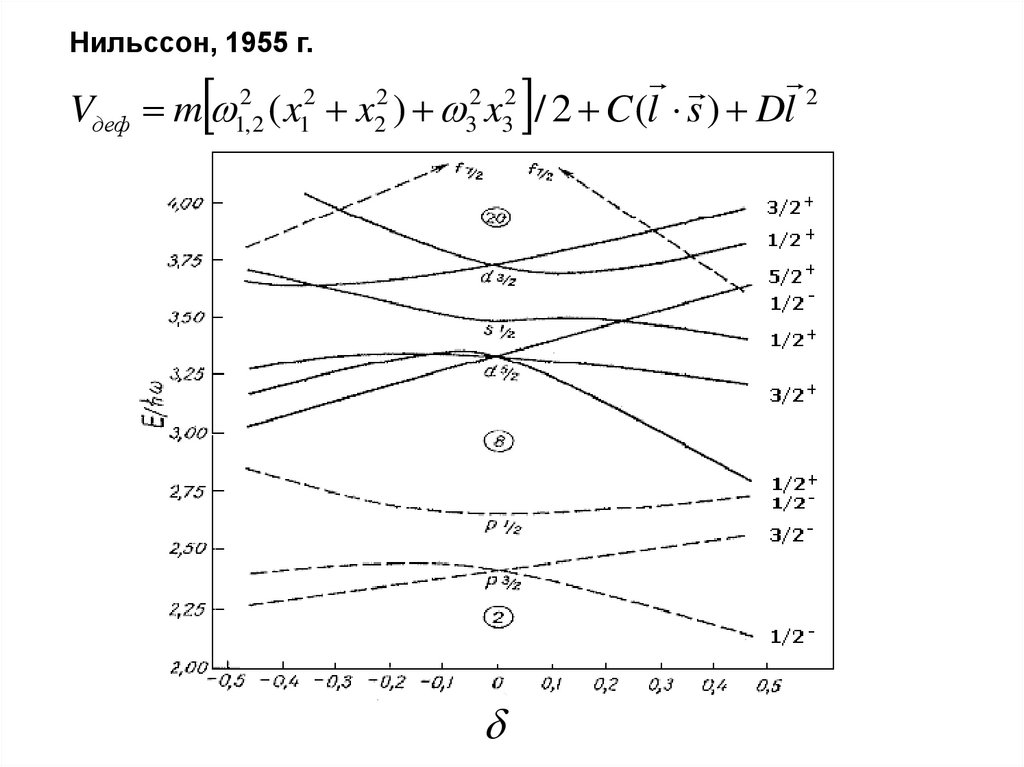
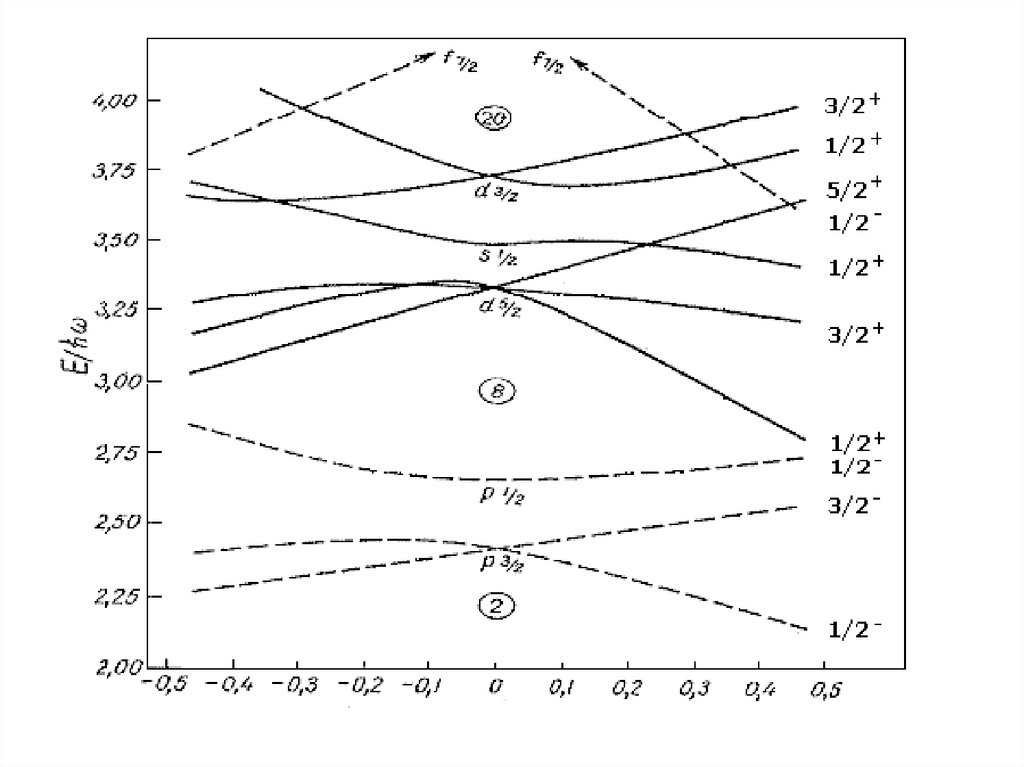
Нильссон, 1955 г.2
Vдеф m ( x x ) x / 2 C (l s ) Dl
2
1, 2
2
1
2
2
2 2
3 3
34.
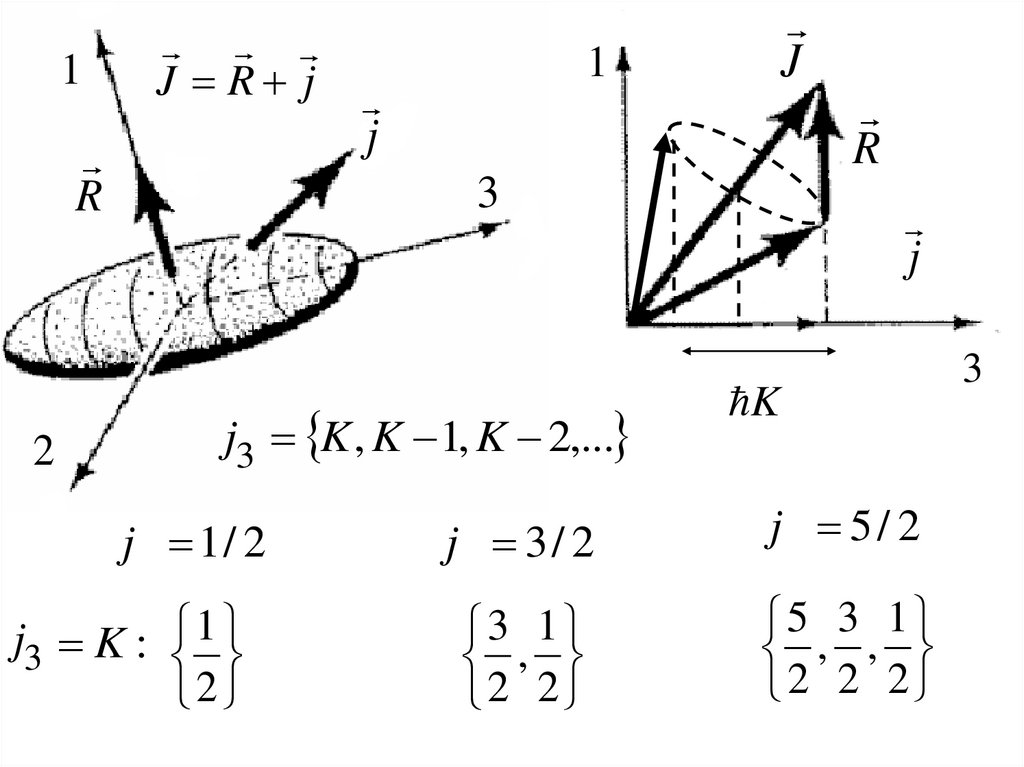
1J R j
R
2
J
1
j
3
j3 K , K 1, K 2,...
R
j
K
j 1/ 2
j 3/ 2
j 5/ 2
j3 K : 1
2
3 1
,
2 2
5 3 1
, ,
2 2 2
3
35.
36.
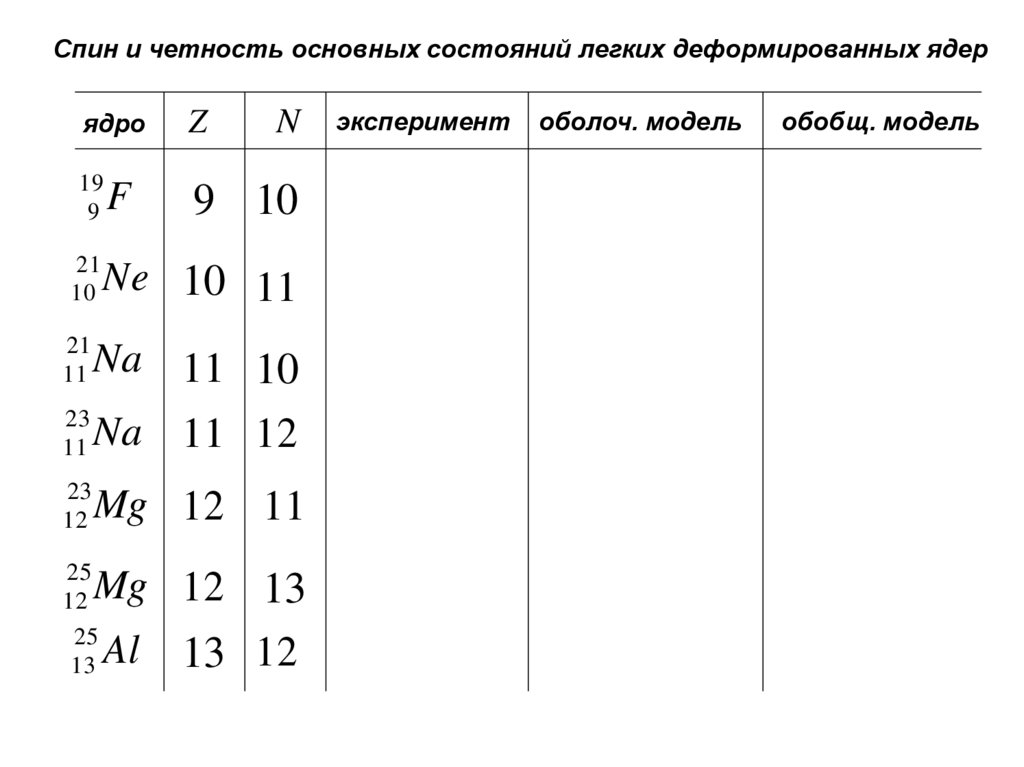
Спин и четность основных состояний легких деформированных ядерN
ядро
Z
19
9
9 10
21
10
F
Ne 10 11
21
11
Na 11 10
23
11 12
11 Na
23
12
Mg 12 11
25
12
25
13
Mg 12 13
Al 13 12
эксперимент
оболоч. модель
обобщ. модель
37.
2s1 / 21d5 / 2
1p1 / 2
1p3 / 2
1s1 / 2
n
19
9
F
p
5
j
2
P
38.
Спин и четность основных состояний легких деформированных ядерядро
19
9
21
10
F
Z
N
9 10
Ne 10 11
21
11
Na 11 10
23
11 12
11 Na
23
12
Mg 12 11
25
12
25
13
Mg 12 13
Al 13 12
эксперимент
(1 / 2)
оболоч. модель
(5 / 2)
обобщ. модель
39.
40.
Спин и четность основных состояний легких деформированных ядерядро
19
9
21
10
F
Z
N
9 10
Ne 10 11
21
11
Na 11 10
23
11 12
11 Na
23
12
Mg 12 11
25
12
25
13
Mg 12 13
Al 13 12
эксперимент
(1 / 2)
оболоч. модель
(5 / 2)
обобщ. модель
(1 / 2)
41.
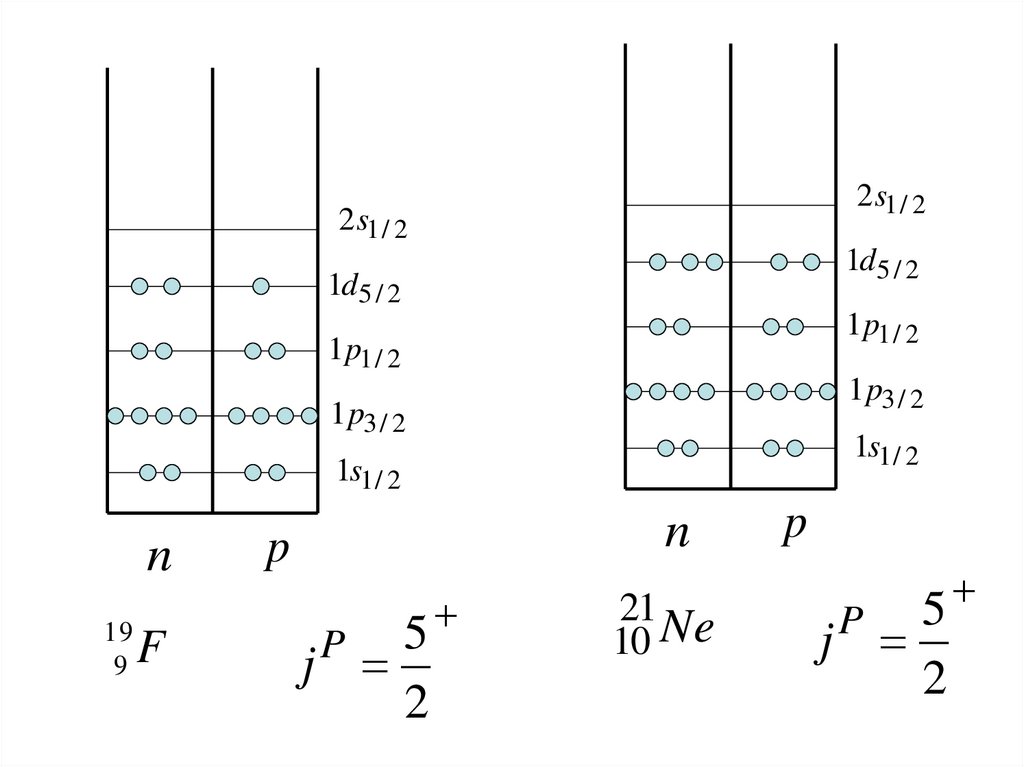
2s1 / 22s1 / 2
1d5 / 2
1d5 / 2
1p1 / 2
1p1 / 2
1p3 / 2
1p3 / 2
1s1 / 2
1s1 / 2
n
19
9
F
n
p
5
j
2
P
21
10 Ne
p
5
j
2
P
42.
43.
Спин и четность основных состояний легких деформированных ядерядро
19
9
21
10
F
Z
N
9 10
Ne 10
11
21
11
Na 11 10
23
11 12
11 Na
23
12
Mg 12 11
25
12
25
13
Mg 12 13
Al 13 12
эксперимент
(1 / 2)
(3 / 2)
оболоч. модель
(5 / 2)
(5 / 2)
обобщ. модель
(1 / 2)
(3 / 2)
44.
Спин и четность основных состояний легких деформированных ядерN
ядро
Z
19
9
9 10
21
10
F
Ne 10 11
эксперимент
оболоч. модель
(1 / 2)
(5 / 2)
(1 / 2)
(3 / 2)
21
11
Na 11 10
23
11 12
11 Na
(5 / 2)
(3 / 2)
(3 / 2)
23
Mg
12 11 (3 / 2)
12
(5 / 2)
(5 / 2)
(5 / 2)
Mg 12 13 (5 / 2)
Al 13 12 (5 / 2)
(5 / 2)
(5 / 2)
25
12
25
13
обобщ. модель
(3 / 2)
(3 / 2)
(3 / 2)
(3 / 2)
(5 / 2)
(5 / 2)



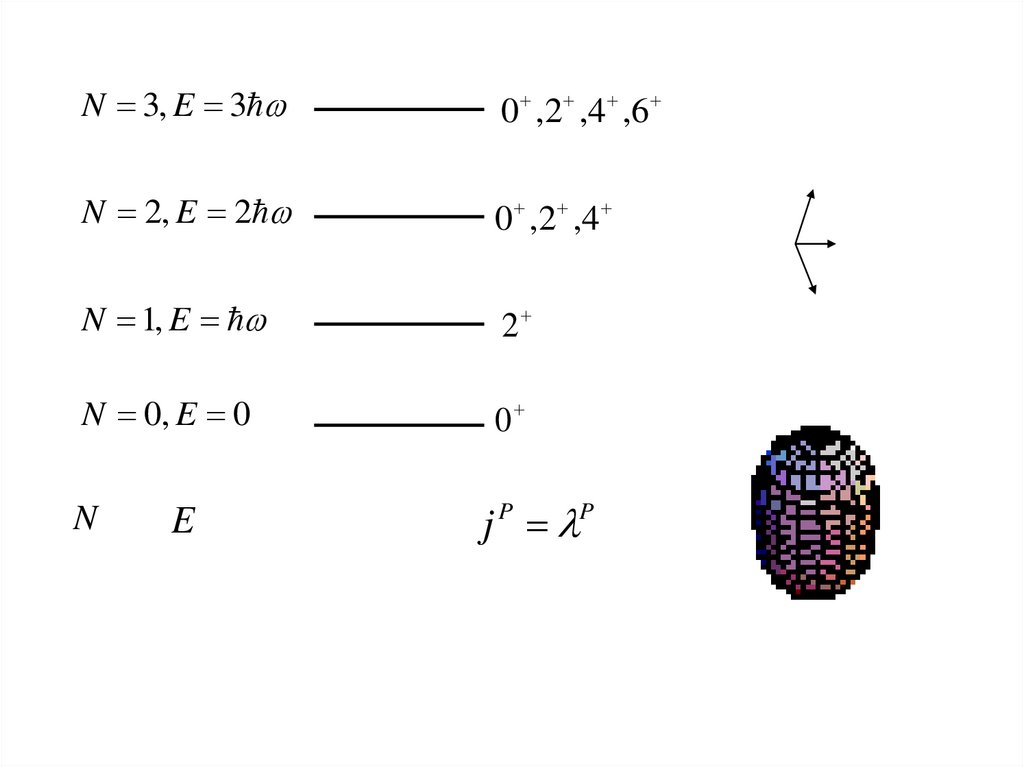
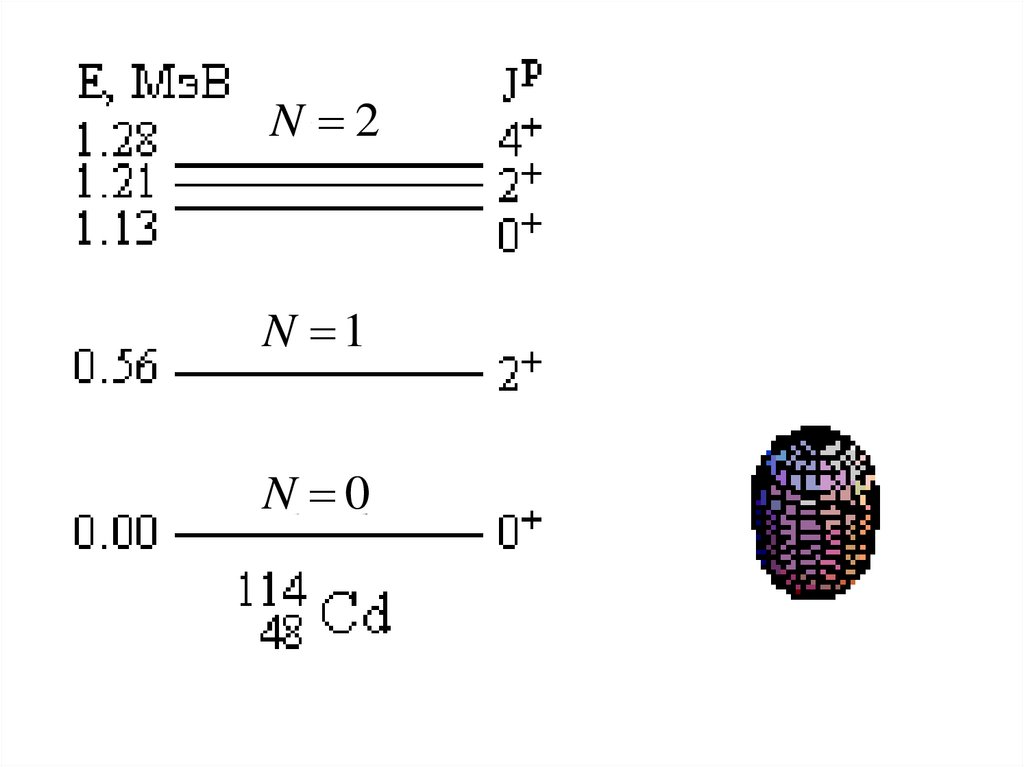





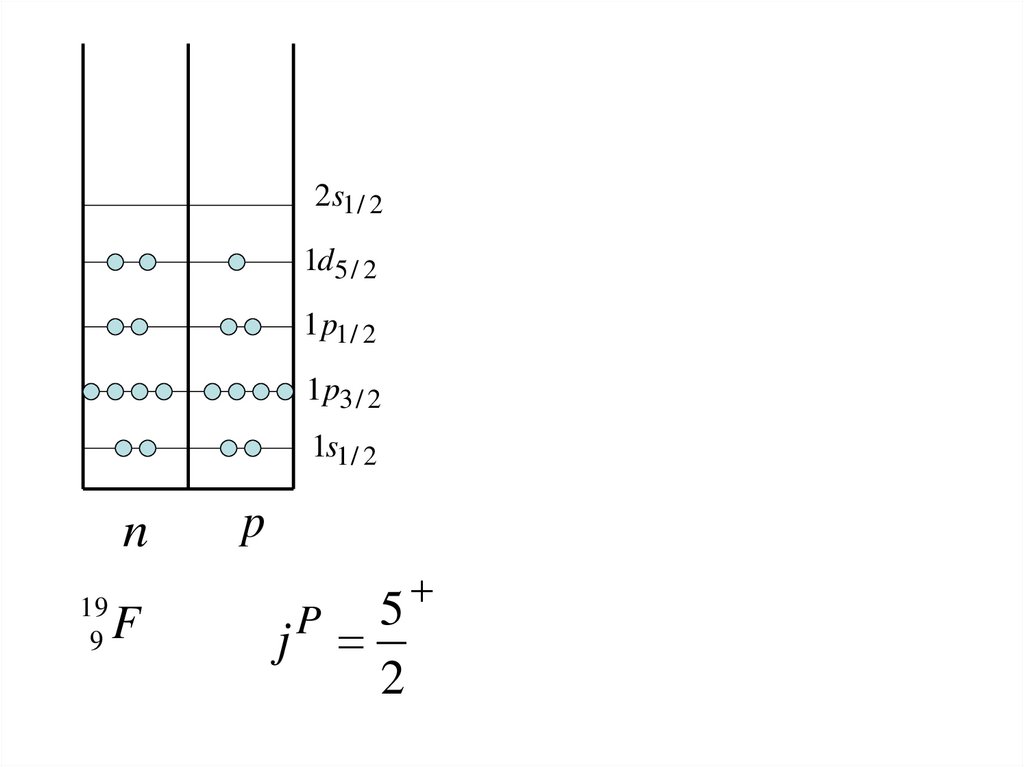




 Физика
Физика








