Похожие презентации:
Молекулярная физика. Основные положения МКТ (тема VI)
1. ТЕМА VI. МОЛЕКУЛЯРНАЯ ФИЗИКА
§1. ОСНОВНЫЕ ПОНЯТИЯ МКТ2. ОСНОВНЫЕ ПОЛОЖЕНИЯ МКТ (I)
1. ОСНОВНЫЕПОЛОЖЕНИЯ МКТ (I)
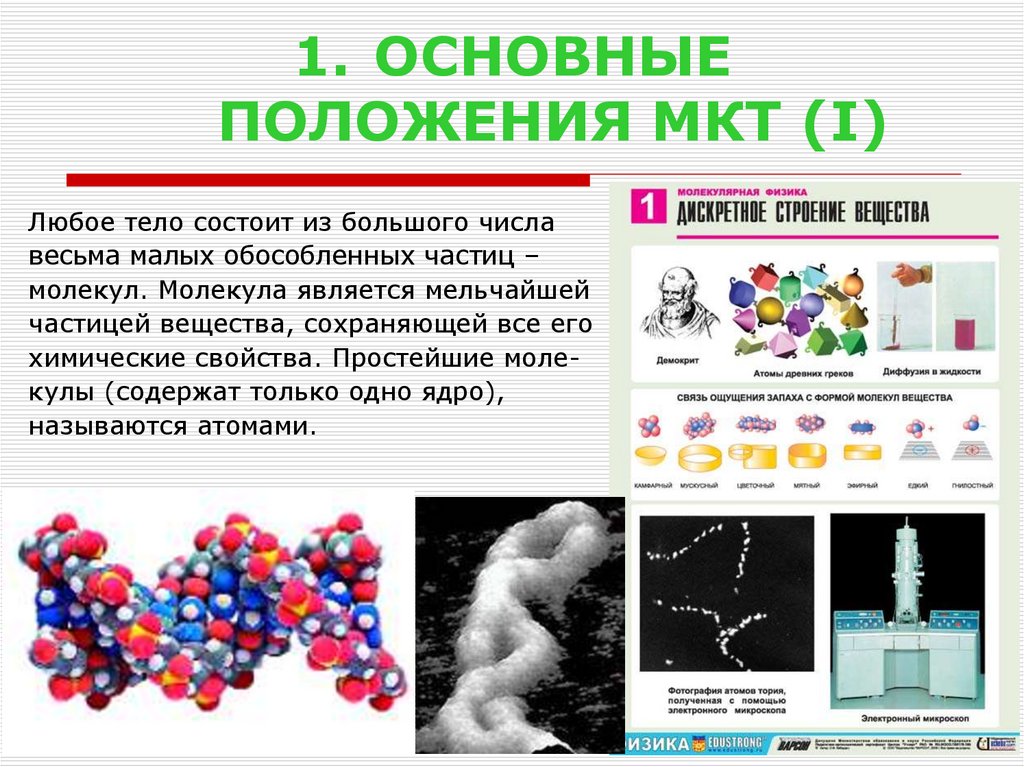
Любое тело состоит из большого числа
весьма малых обособленных частиц –
молекул. Молекула является мельчайшей
частицей вещества, сохраняющей все его
химические свойства. Простейшие молекулы (содержат только одно ядро),
называются атомами.
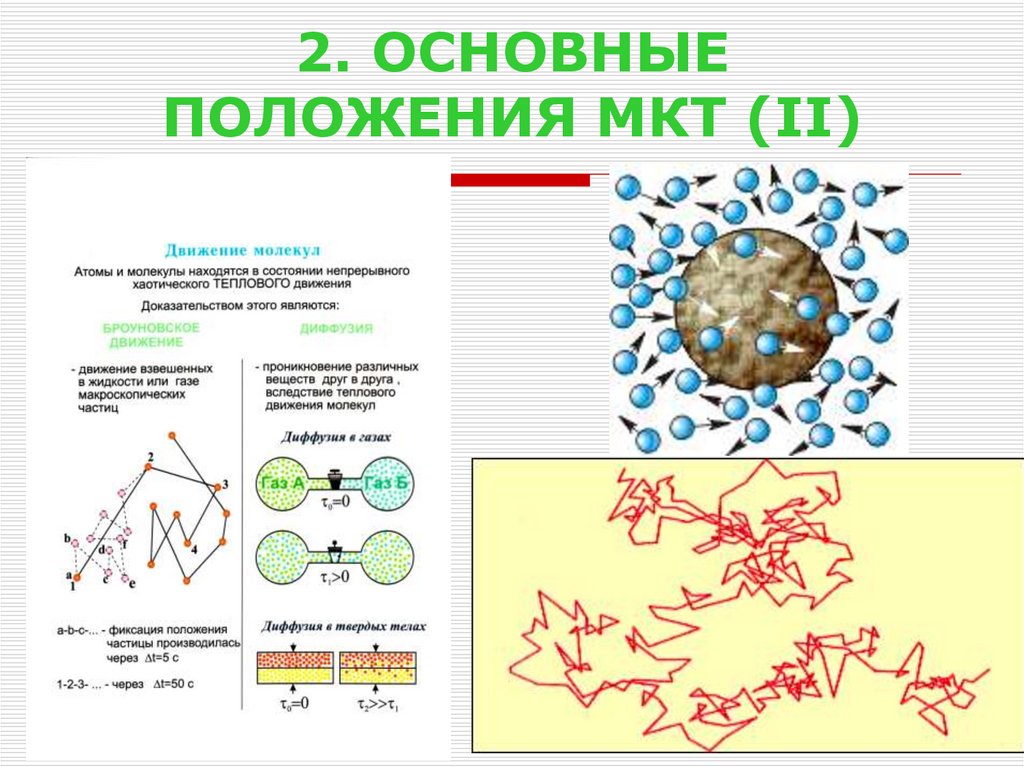
3. 2. ОСНОВНЫЕ ПОЛОЖЕНИЯ МКТ (II)
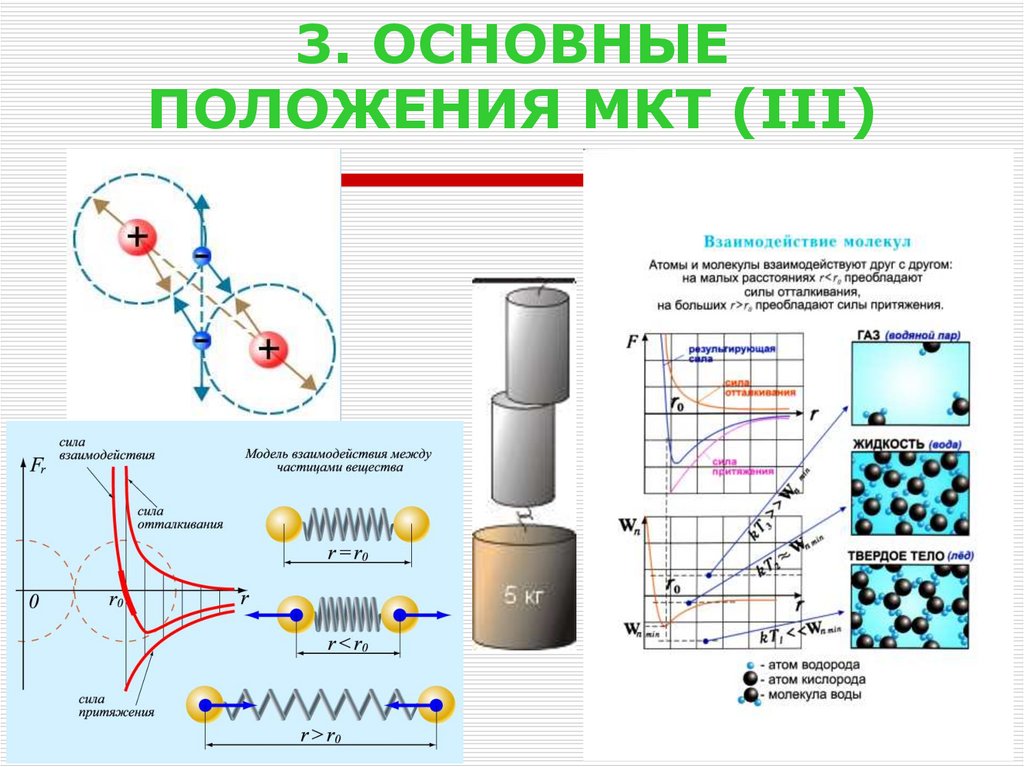
4. 3. ОСНОВНЫЕ ПОЛОЖЕНИЯ МКТ (III)
5. 4. КОЛИЧЕСТВО ВЕЩЕСТВА
Амедео Авогадро1776-1856
Итальянский
физик и химик
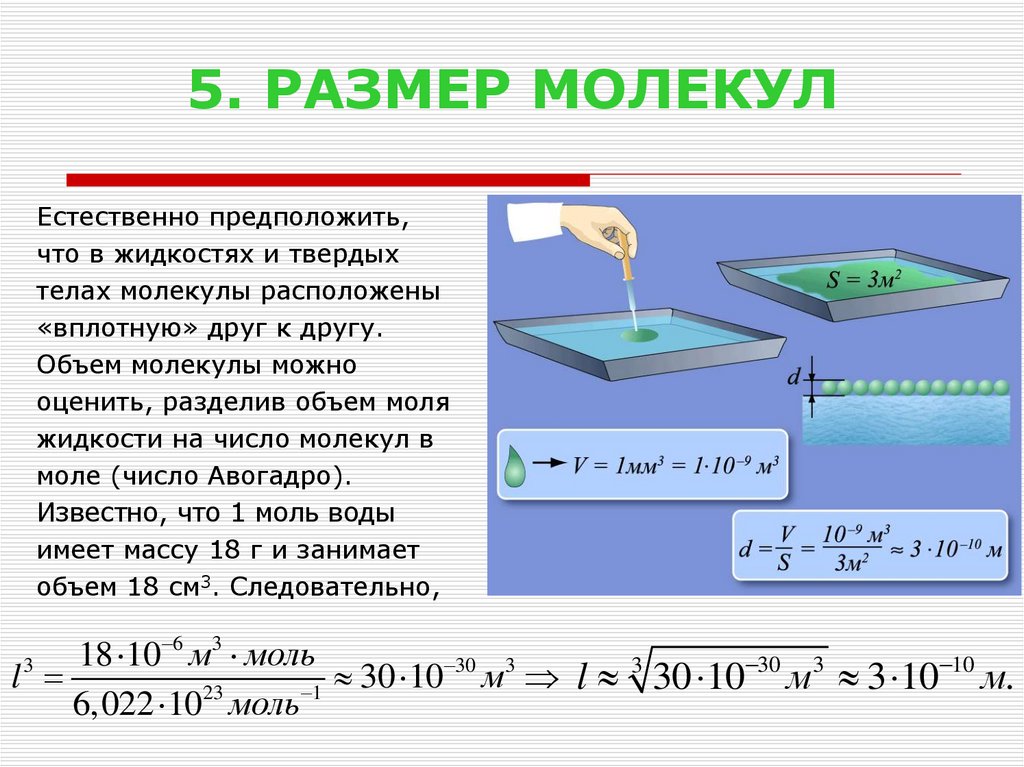
6. 5. РАЗМЕР МОЛЕКУЛ
Естественно предположить,что в жидкостях и твердых
телах молекулы расположены
«вплотную» друг к другу.
Объем молекулы можно
оценить, разделив объем моля
жидкости на число молекул в
моле (число Авогадро).
Известно, что 1 моль воды
имеет массу 18 г и занимает
объем 18 см3. Следовательно,
18 10 6 м3 моль
30 3
10
30 3
3
l
30
10
м
l 30 10 м 3 10 м.
23
1
6,022 10 моль
3
7. 6. СТАТИСТИЧЕСКИЙ И ТЕРМОДИНАМИЧЕСКИЙ МЕТОДЫ
Существуют два способа описания процессов, происходящих в макроскопических телах (телах, состоящих из большого числа частиц) –статистический и термодинамический. Статистический метод изучает
свойства макроскопических тел исходя из свойств образующих тело
частиц и взаимодействий между ними. Свойства тел, наблюдаемые на
опыте, объясняются как усредненный результат действия
отдельных молекул. Термодинамический метод изучает свойства
тел, не вдаваясь в их микроскопическую структуру, а опираясь
на фундаментальные законы
(начала термодинамики), установленные обобщением экспериментальных фактов.
8. 7. ТЕРМОДИНАМИЧЕСКАЯ СИСТЕМА. ПАРАМЕТРЫ СОСТОЯНИЯ
Термодинамической системойназывается совокупность
макроскопических тел, которые
могут обмениваться энергией
между собой и окружающей средой.
Термодинамическая система может
находиться в различных состояниях,
различающихся температурой,
давлением, объемом, плотностью…
Подобные величины, характерезующие состояние системы, называются параметрами состояниями.
Термодинамические системы, которые
не обмениваются с внешней средой
ни энергией, ни веществом называются замкнутыми (изолированными).
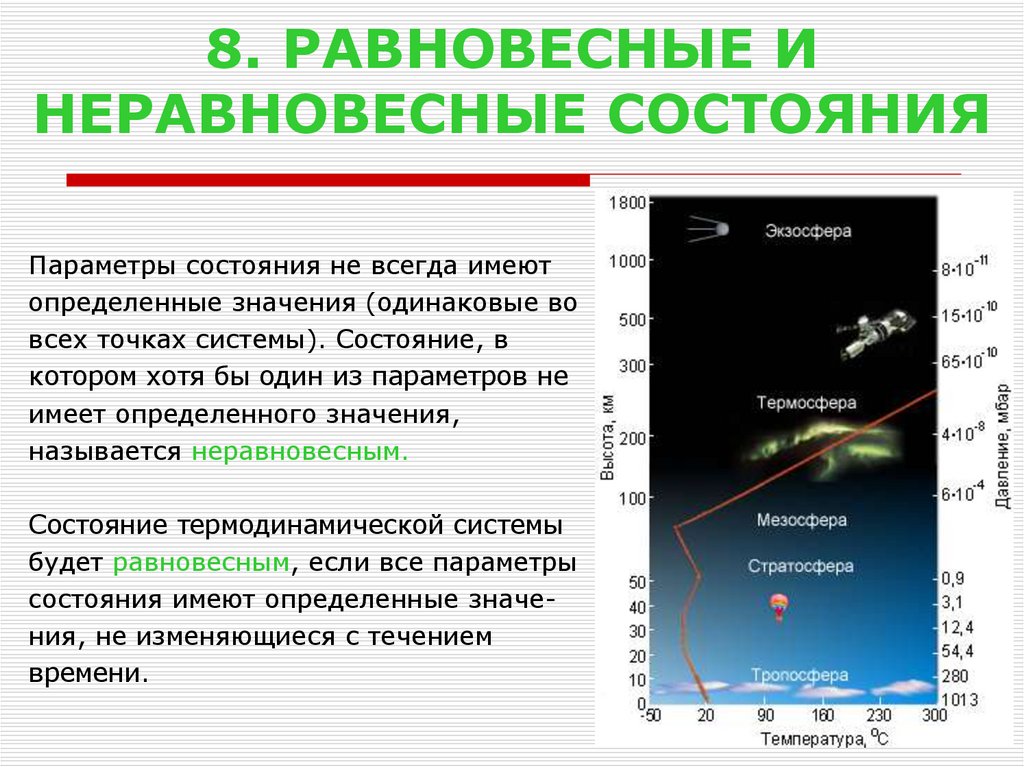
9. 8. РАВНОВЕСНЫЕ И НЕРАВНОВЕСНЫЕ СОСТОЯНИЯ
Параметры состояния не всегда имеютопределенные значения (одинаковые во
всех точках системы). Состояние, в
котором хотя бы один из параметров не
имеет определенного значения,
называется неравновесным.
Состояние термодинамической системы
будет равновесным, если все параметры
cостояния имеют определенные значения, не изменяющиеся с течением
времени.
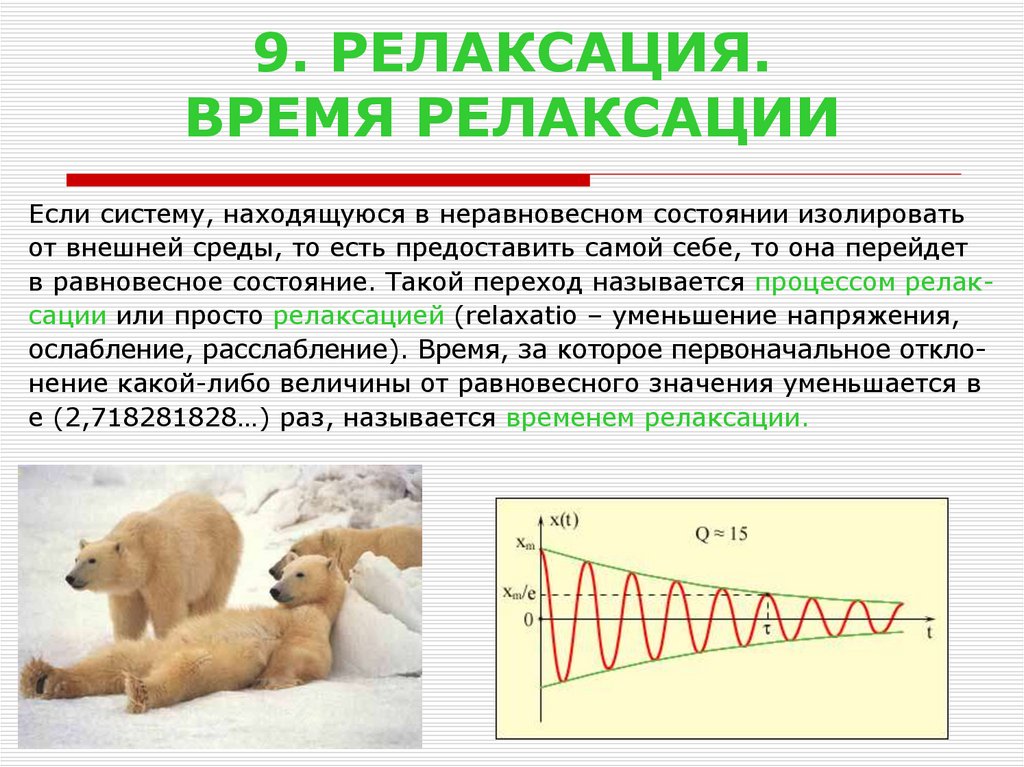
10. 9. РЕЛАКСАЦИЯ. ВРЕМЯ РЕЛАКСАЦИИ
Если систему, находящуюся в неравновесном состоянии изолироватьот внешней среды, то есть предоставить самой себе, то она перейдет
в равновесное состояние. Такой переход называется процессом релаксации или просто релаксацией (relaxatio – уменьшение напряжения,
ослабление, расслабление). Время, за которое первоначальное отклонение какой-либо величины от равновесного значения уменьшается в
e (2,718281828…) раз, называется временем релаксации.
11. 10. РАВНОВЕСНЫЕ ПРОЦЕССЫ
Термодинамическим процессом называетсяпереход системы из одного состояния в другое.
Такой переход всегда связан с нарушением
равновесия системы. Например, при сжатии
газа давление в первую очередь возрастет
вблизи поршня – равновесие нарушится.
Нарушение равновесия будет тем значительнее,
чем быстрее перемещать поршень. Если двигать
поршень очень медленно, то равновесие нарушается незначительно и давление в разных
точках мало отличается от равновесного для
данного объема газа. В пределе, при бесконечно
медленном сжатии процесс окажется состоящим
из последовательности равновесных состояний.
Такой процесс называется равновесным или
квазистатическим.
12. 11. ОБРАТИМЫЕ И НЕОБРАТИМЫЕ ПРОЦЕССЫ
При изменении направления равновесногопроцесса (например, замене сжатия газа
расширением) система будет проходить
через те же равновесные состояния, что и
при прямом ходе, но в обратной последовательности. Поэтому равновесные процессы
называют также обратимыми процессами.
Равновесное состояние можно изобразить
точкой на координатной (фазовой) плоскости, а равновесный процесс – кривой линией.
Неравновесное состояние и процесс не могут
быть изображенными таким способом.
Неравновесные процессы являются
необратимыми процессами.
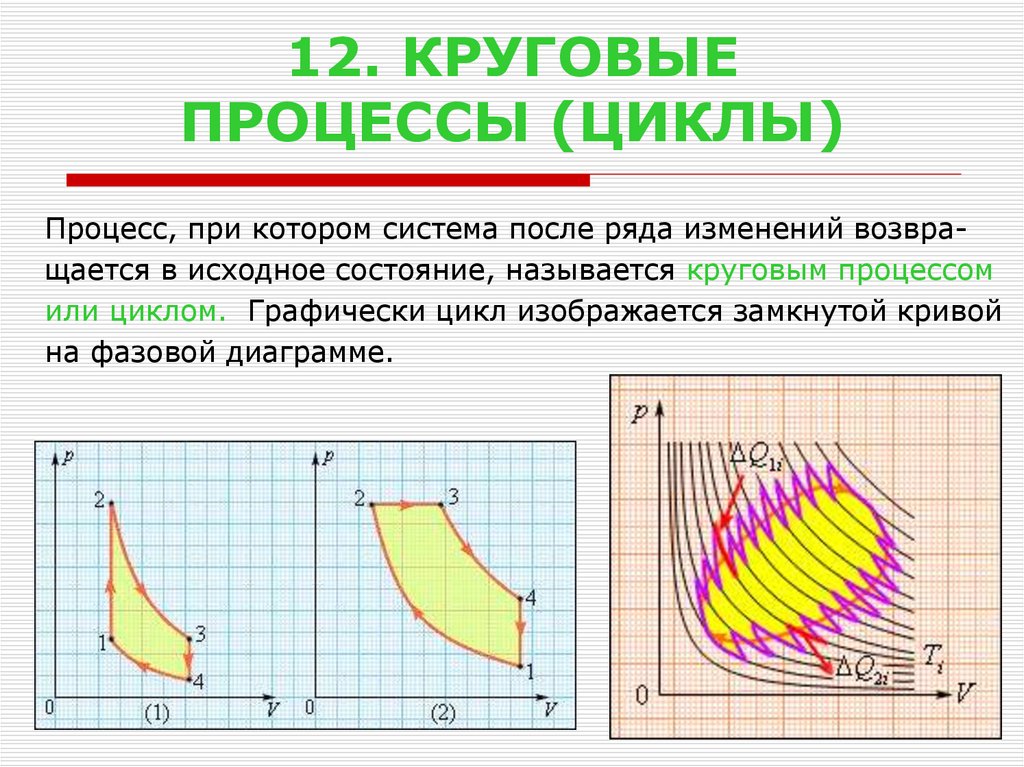
13. 12. КРУГОВЫЕ ПРОЦЕССЫ (ЦИКЛЫ)
Процесс, при котором система после ряда изменений возвращается в исходное состояние, называется круговым процессомили циклом. Графически цикл изображается замкнутой кривой
на фазовой диаграмме.
14. 13. ТЕМПЕРАТУРА
Если два тела находятся в состояниитермодинамического равновесия, то
есть не обмениваются энергией путем
теплопередачи, то этим телам приписывается одинаковая температура.
Если между телами происходит направленный теплообмен, то телу отдающему
энергию приписывают большую температуру по сравнению с телом, получающим тепловую энергию.
Ряд свойств тел – объем, давление,
электрическое сопротивление – зависит
от температуры. Любое из этих свойств
Можно использовать для количественного определения температуры.
15. 14. УРВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
Параметры состояния термодинамическойсистемы закономерно связаны между
собой. Соотношение, определяющее связь
между параметрами состояния системы,
называется уравнением состояния.
Газ, взаимодействием между молекулами
которого можно пренебречь, называется
идеальным газом.
Опытным путем было установлено, что
при обычных условиях (комнатная температура, атмосферное давление) газы
подчиняются уравнению
pV
const
T
N.
16. 15. ЗАКОН ШАРЛЯ
Жан Александр Шарль1746-1823
французский физик и
изобретатель
17. 16. ЗАКОН БОЙЛЯ-МАРИОТТА
Роберт Бойль1627-1691
английский химик,
физик и теолог
Эдм Мариотт
1620-1684
французский
физик
18. 17. ЗАКОН ГЕЙ-ЛЮССАКА
Жозеф Луи Гей-Люссак1778-1850
французский химик и
физик
19. 18. ЗАКОН ДАЛЬТОНА
Джон Дальтон1766-1844
английский физик
20. 19. РЕАЛЬНЫЕ ГАЗЫ
21. §2. СТАТИСТИЧЕСКАЯ ФИЗИКА
22. 1.ЧИСЛО МОЛЕКУЛ, ДВИЖУЩИХСЯ В ЗАДАННОМ НАПРАВЛЕНИИ
Хаотичность движения молекул приводит к тому, что распределениемолекул по направлениям является равномерным. Тогда, количество
молекул, движущихся в пределах бесконечно малого телесного угла
N
dS
dN
d ; d 2 ; dS rd r sin d r 2 sin d d
4
r
N
sin d d .
d sin d d dN
4
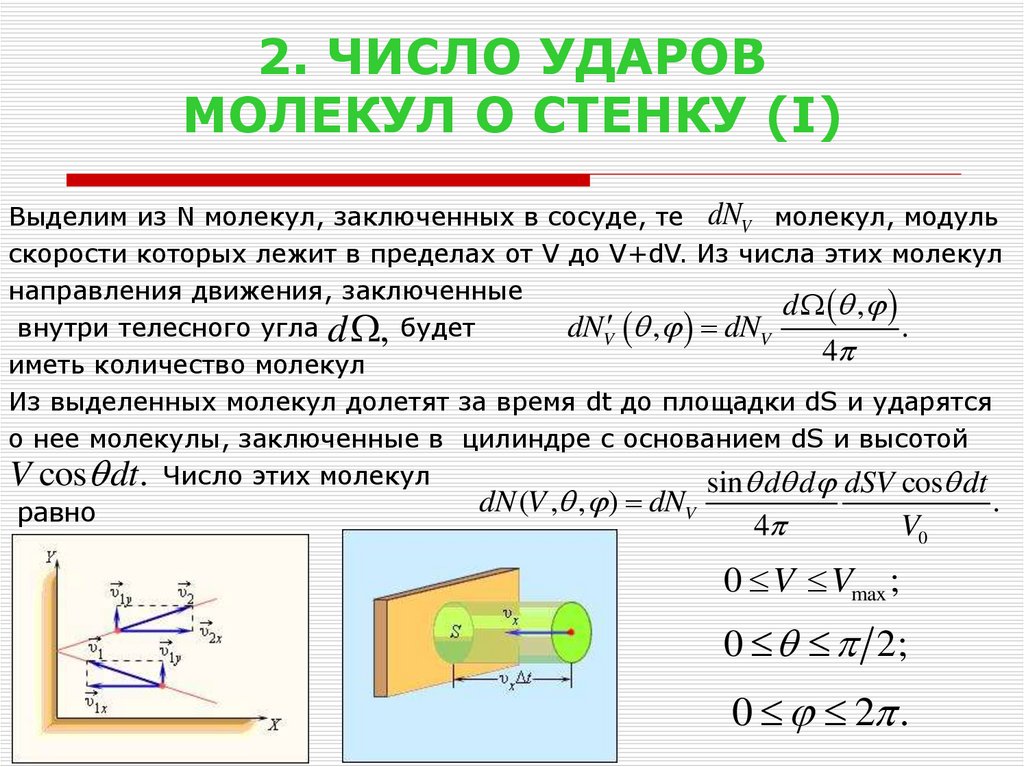
23. 2. ЧИСЛО УДАРОВ МОЛЕКУЛ О СТЕНКУ (I)
Выделим из N молекул, заключенных в сосуде, те dNV молекул, модульскорости которых лежит в пределах от V до V+dV. Из числа этих молекул
направления движения, заключенные
d ,
внутри телесного угла d , будет
dNV , dNV
.
4
иметь количество молекул
Из выделенных молекул долетят за время dt до площадки dS и ударятся
о нее молекулы, заключенные в цилиндре с основанием dS и высотой
V cos dt. Число этих молекул
sin d d dSV cos dt
dN
(
V
,
,
)
dN
.
V
равно
4
V0
0 V Vmax ;
0 2;
0 2 .
24. 3. ЧИСЛО УДАРОВ МОЛЕКУЛ О СТЕНКУ (II)
dN (V , , ) dNVsin d d dSV cos dt
4
V0
2
V
2
dSdt max
dN
VdNV sin cos d d
4 V0 0
0
0
dN
Vmax
2
dSdt N
dNV
V
sin d sin 2
4 V0 0
N 0
2
sin 2
dN
1N
1 N max
VdPV
VdPV .
dSdt 2 V0 0
4 V0 0
2 0
Vmax
dN
;
dSdt
V
V
N
n; VdPV Vср
V0
0
max
1
nVср .
4
25. 4. ДАВЛЕНИЕ ГАЗА НА СТЕНКУ (I)
Стенки сосуда, в котором заключен газ, подвергаются непрерывнойбомбардировке молекулами. Если предположить, что молекулы отскакивают от стенки по закону зеркального отражения и модуль скорости
молекулы не изменяется, то импульс, сообщаемый стенке молекулой
при ударе равен 2m0V cos . Импульс, передаваемый поверхности dS
за время dt, молекулами движущимися в пределах
телесного угла d ( , ) sin d d со скоростью в интервале от V до V+dV, будет равен
sin d d V cos dtdS
dK V , , 2m0V cos dNV
4
V0
dK V , , m0V 2 dNV
cos 2 sin d d ;
dtdS
2 V0
0 V Vm ;
0 2;
0 2 .
26. 5. ДАВЛЕНИЕ ГАЗА НА СТЕНКУ (II)
Проинтегрируем выражение для импульсапо всем возможным скоростям и направлениям движения молекул:
V
2
V
2
2
dK
m0 m 2
2
V
dN
cos
sin d d
V
dtdS 2 V0 0
0
0
dF m0 N m 2 dNV
2
V
cos
d cos 2
dS 2 V0 0
N 0
2
cos
p m0 n V dPV
;
3 0
0
Vm
3
2
Vm
1
2
p
m
n
V
.
V
dP
V
0
0 V ср
ср
3
2
2
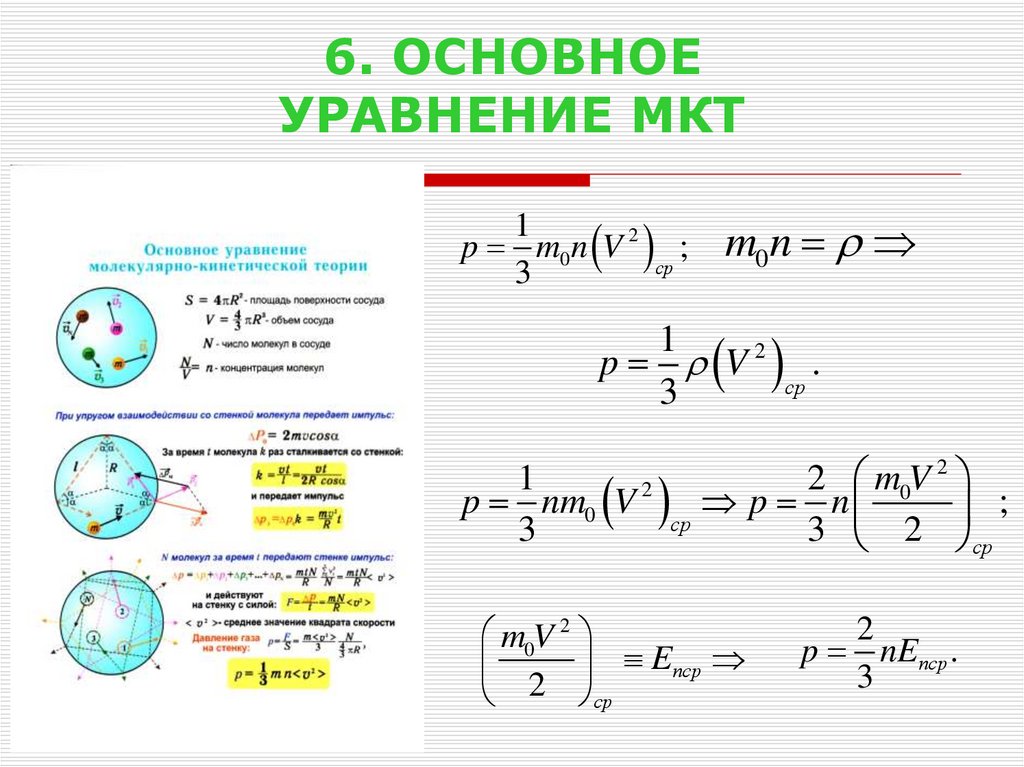
27. 6. ОСНОВНОЕ УРАВНЕНИЕ МКТ
1p m0 n V 2 ;
ср
3
m0 n
1
p V 2 .
ср
3
2
1
2
m
V
2
0
p nm0 V p n
;
ср
3
3 2 ср
m0V 2
2 Eпср
ср
2
p nEпср .
3
28. 7. СРЕДНЯЯ ЭНЕРГИЯ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ
mpV
RT ;
M
NA N
m
M
pV N AkT ;
pV NkT
N
p
kT ;
V
N
n
V
2
p nEпср
3
p nkT .
2
nEпср nkT
3
3
Eпср kT .
2
Температура есть величина, пропорциональная средней
кинетической энергии поступательного движения молекул.
Отметим, что эта энергия не зависит от массы молекул.
29. 8. СРЕДНЯЯ КВАДРАТИЧНАЯ СКОРОСТЬ
3Eпср kT ;
2
k 1,38 10
m0 2
3
V kT
ср
2
2
V V
2
ср
кв
23
Дж
;
К
m0 2
Eпср
V
ср
2
3kT 3kN AT 3RT
V ср m m N M .
0
0 A
2
3kT
3RT
Vкв
.
m0
M
30. 9. ЗАКОН РАВНОРАСПРЕДЕЛЕНИЯ
m0 2Eпср
V ;
ср
2
V 2 Vx2 Vy2 Vz2 V 2 Vx2 Vy2 Vz2 ;
ср
V V V V 2 ср 3 Vx2 ср
2
x ср
2
y ср
3
Eпср kT
2
2
z cр
3
kT 3
2
m0 Vx2
2
ср
ср
ср
ср
3
Eпср m0 Vx2 .
ср
2
m0 Vx2
2
ср
kT
.
2
В классической статистической физике вводится закон равнораспределения энергии по степеням свободы, согласно которому в состоянии
термодинамического равновесия на каждую степень свободы молекулы
приходится в среднем энергия, равная kT/2.
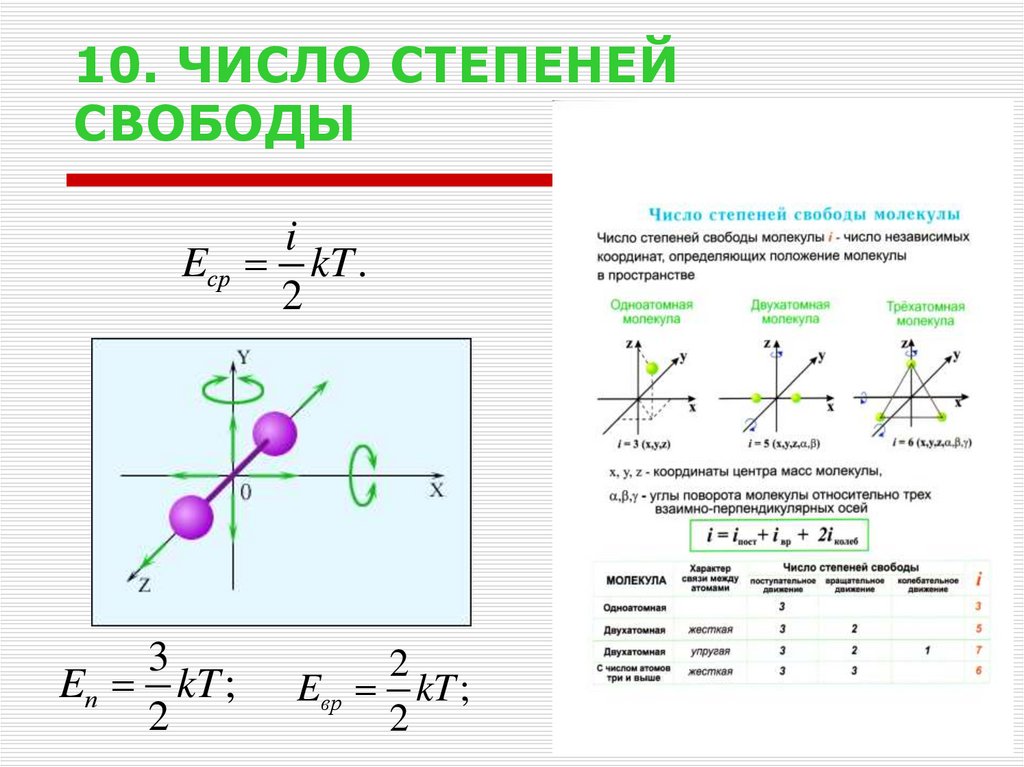
31. 10. ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ
iEср kT .
2
3
Eп kT ;
2
2
Eвр kT ;
2






















 Физика
Физика








