Похожие презентации:
Теорема Пифагора
1.
Древнегреческийфилософ и
математик
(580 - 500 г. до н.э.)
2.
3.
В прямоугольном треугольнике квадрат гипотенузыравен сумме квадратов катетов.
S (a b)
c
b 1
2
c
2
2
1
2
S 4 ab c
2
1
2
2
4 ab c (a b)
2
2ab c 2 (a b) 2
ab
c a b
2
a
2
2
4.
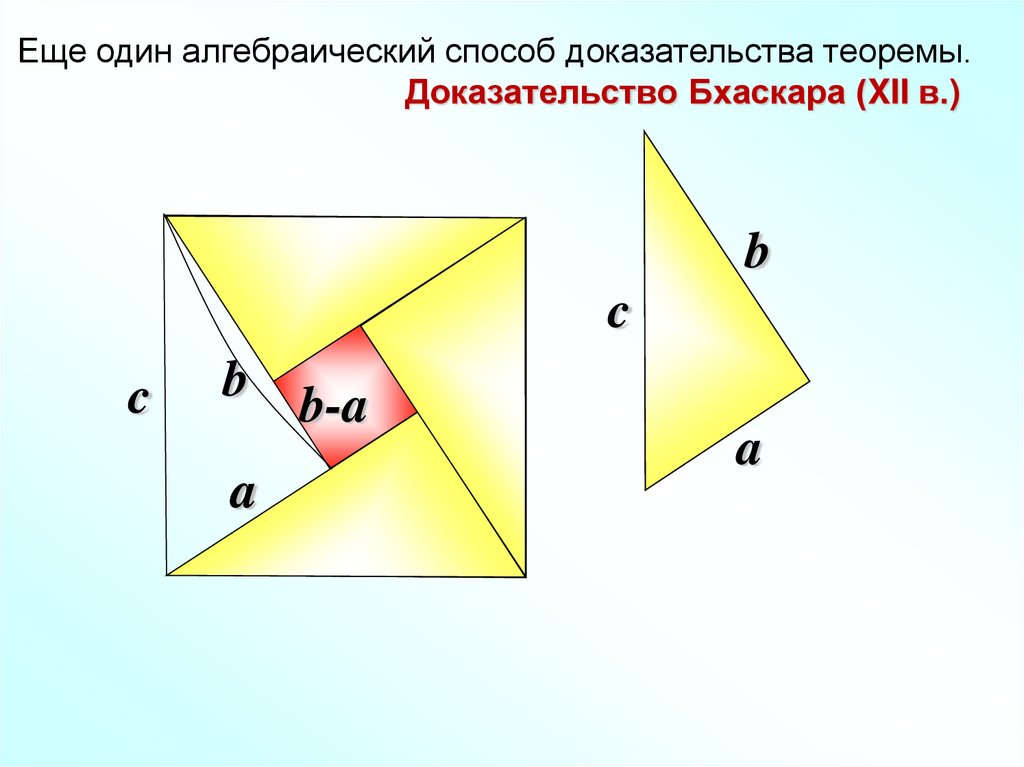
Еще один алгебраический способ доказательства теоремы.Доказательство Бхаскара (XII в.)
b
c
c
b
a
b-a
a
5.
Для прямоугольных треугольников составить равенства,выражающие зависимость между сторонами прямоугольного
треугольника, по теореме Пифагора.
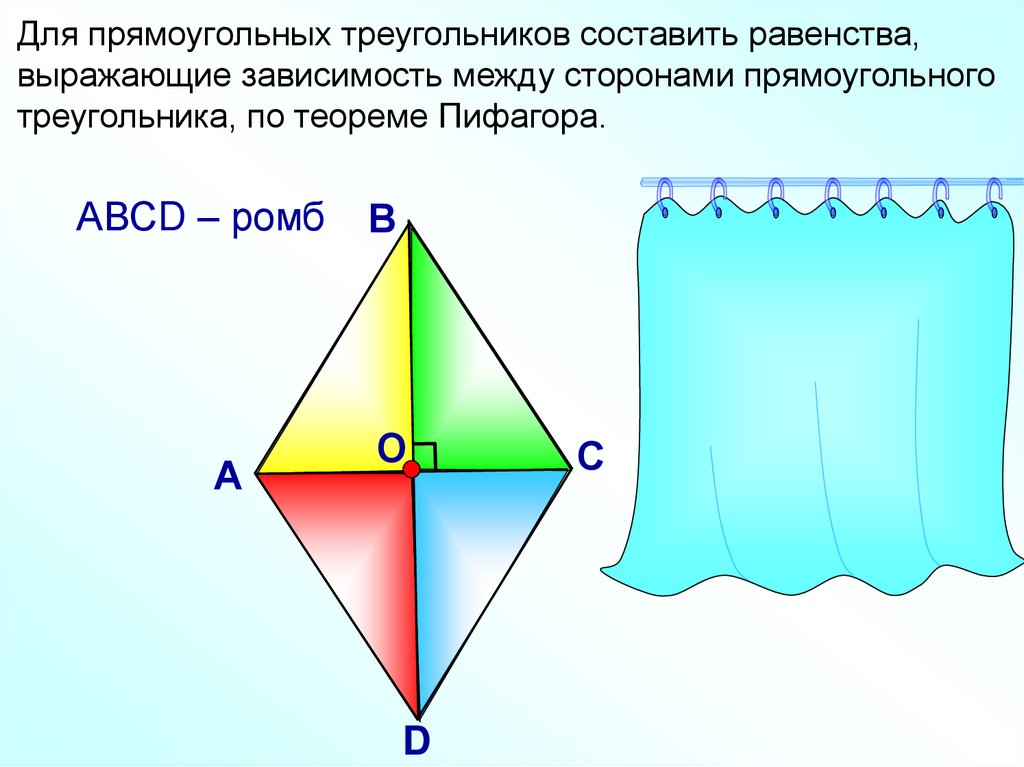
АВСD – ромб
В
АВ2=АО2
+
ВС2 = ВО2 + ОС2
ОВ2
А
О
С
DC2 = DO2 + OC2
АD2 = DO2 + OA2
D
6.
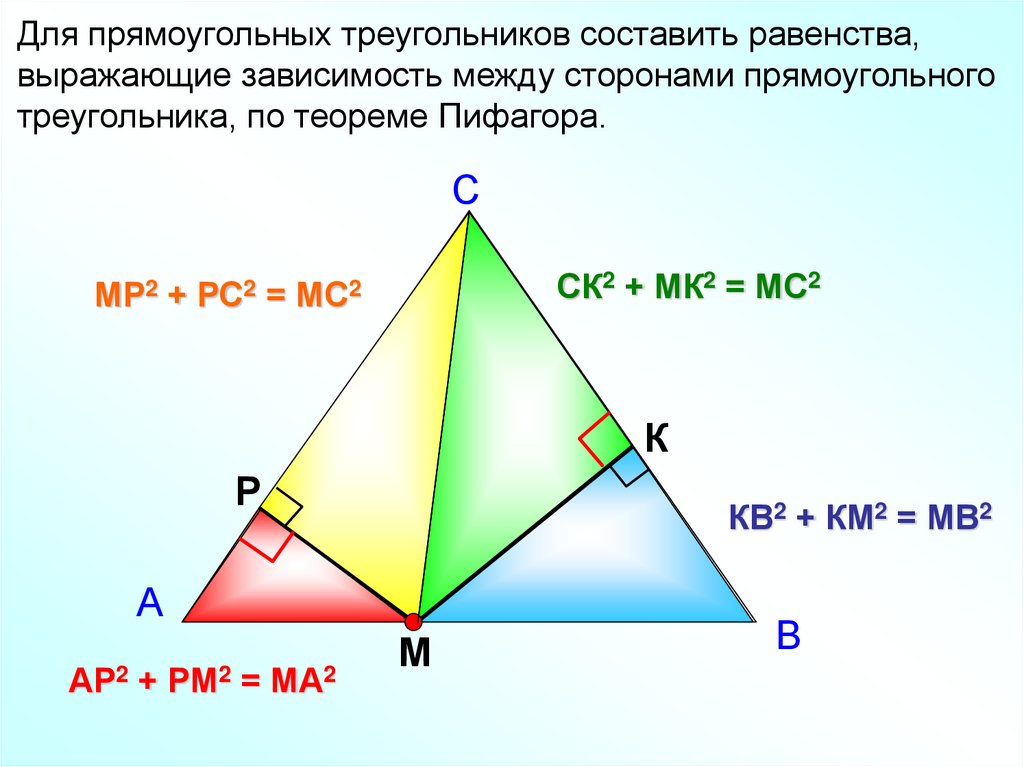
Для прямоугольных треугольников составить равенства,выражающие зависимость между сторонами прямоугольного
треугольника, по теореме Пифагора.
С
МР2
+
РС2
=
СК2 + МК2 = МС2
МС2
К
Р
КВ2 + КМ2 = МВ2
А
АР2 + РМ2 = МА2
М
В
7.
Для прямоугольных треугольников составить равенства,выражающие зависимость между сторонами прямоугольного
треугольника, по теореме Пифагора.
АВСD – ромб
В
АВ2=АО2 + ОВ2
DC2 = DO2 + OC2
А
О
С
АD2 = DO2 + OA2
ВС2 = ВО2 + ОС2
D
8.
Для прямоугольных треугольников составить равенства,выражающие зависимость между сторонами прямоугольного
треугольника, по теореме Пифагора.
С
МР2 + РС2 = МС2
КВ2 + КМ2 = МВ2
АР2 + РМ2 = МА2
К
СК2 + МК2 = МС2
Р
А
М
В
9.
Для прямоугольных треугольников составить равенства,выражающие зависимость между сторонами прямоугольного
треугольника, по теореме Пифагора.
D1
C1 Прямоугольный
параллелепипед
АВСDА1В1С1D1
B1
А1
В1А2 = АВ2 + В1В2
В1С2 = СВ2 + В1В2
D
А
С
В
Заглянем внутрь
параллелепипеда
D1B2 = DВ2 + D1D2






 Математика
Математика








