Векторы

1. Векторы

2. Вектор – направленный отрезок

Примеры векторов в физике:
скорость V;
ускорение a;
перемещение S;
сила F;
импульс тела P;
импульс силы F·∆t;
напряженность электрического
поля E;
вектор магнитной индукции В;
спин.

3.

Вектор имеет:
точку приложения
направление
численное значение
Число, выражающее длину направленного
отрезка, называют модулем вектора и
обозначают той же буквой, что и сам вектор, но
без стрелки наверху, например: модулем вектора
V является число V.
Вектор называется нулевым, если начало и конец
его совпадают.
Векторы называют коллинеарными, если они
лежат либо на одной прямой, либо на
параллельных прямых.

4.

Линейные операции над векторами
Сложение
Вычитание
Умножение на
число

5.

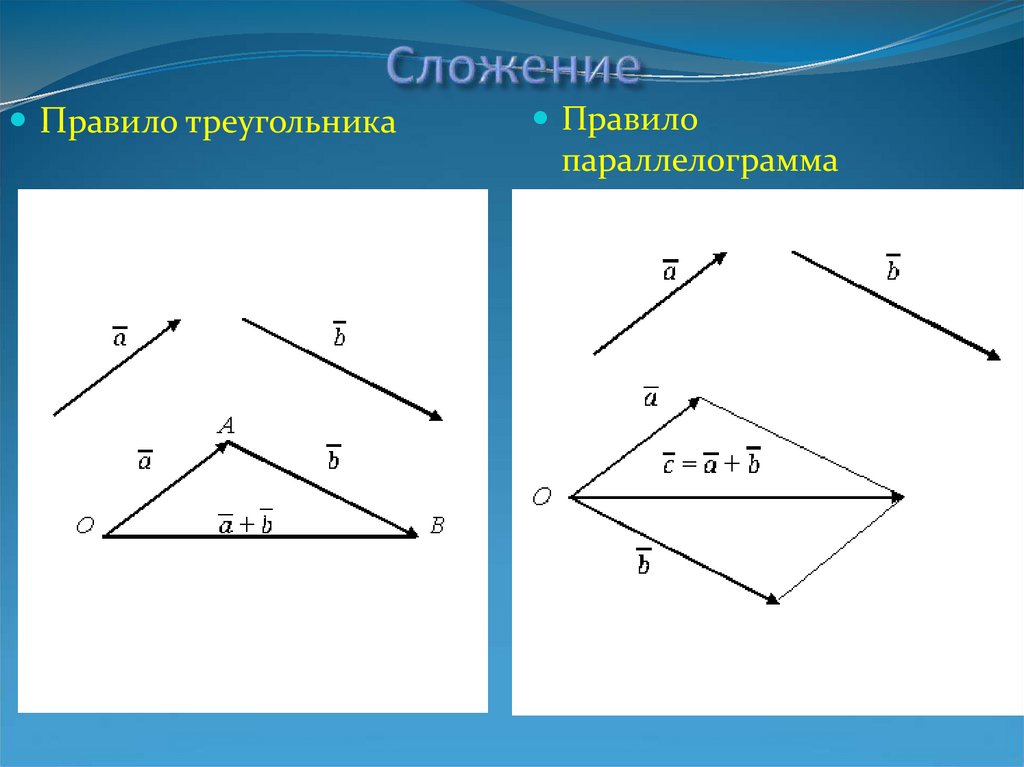
Правило треугольника
Правило
параллелограмма

6.

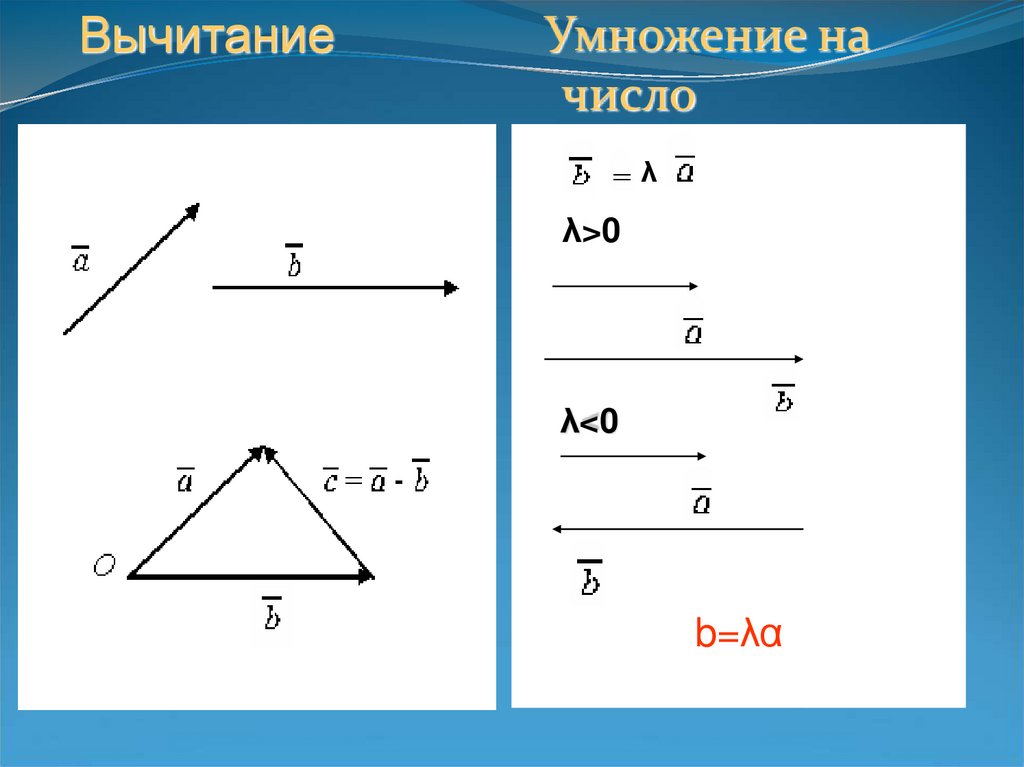
Вычитание
Умножение на
число
λ
λ>0
λ<0
b=λα

7.

Скалярным произведением двух
ненулевых векторов называется число, равное
произведению длин этих векторов на косинус угла
между ними.
а
b

8.

Векторным произведением вектора на вектор называется
вектор , который :
1) перпендикулярен векторам а и b ;
2) имеет длину, численно равную площади
параллелограмма,
построенного на векторах a и b , т.е.
3) векторы a и b образуют правую тройку.

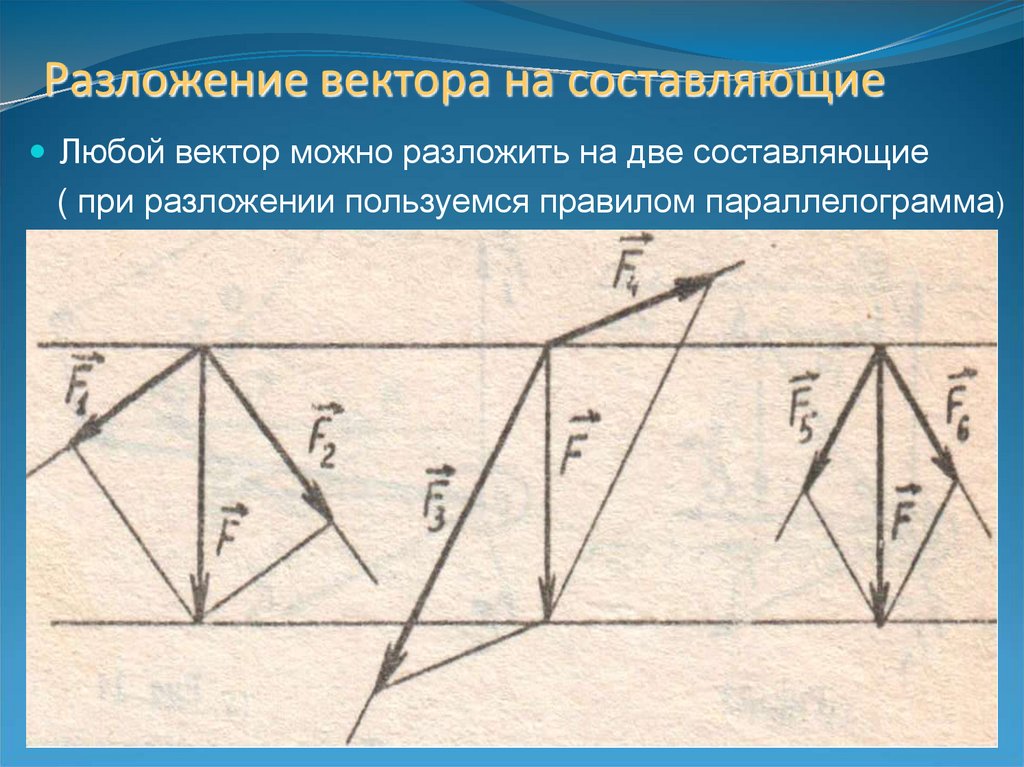
9. Разложение вектора на составляющие

Любой вектор можно разложить на две составляющие
( при разложении пользуемся правилом параллелограмма)

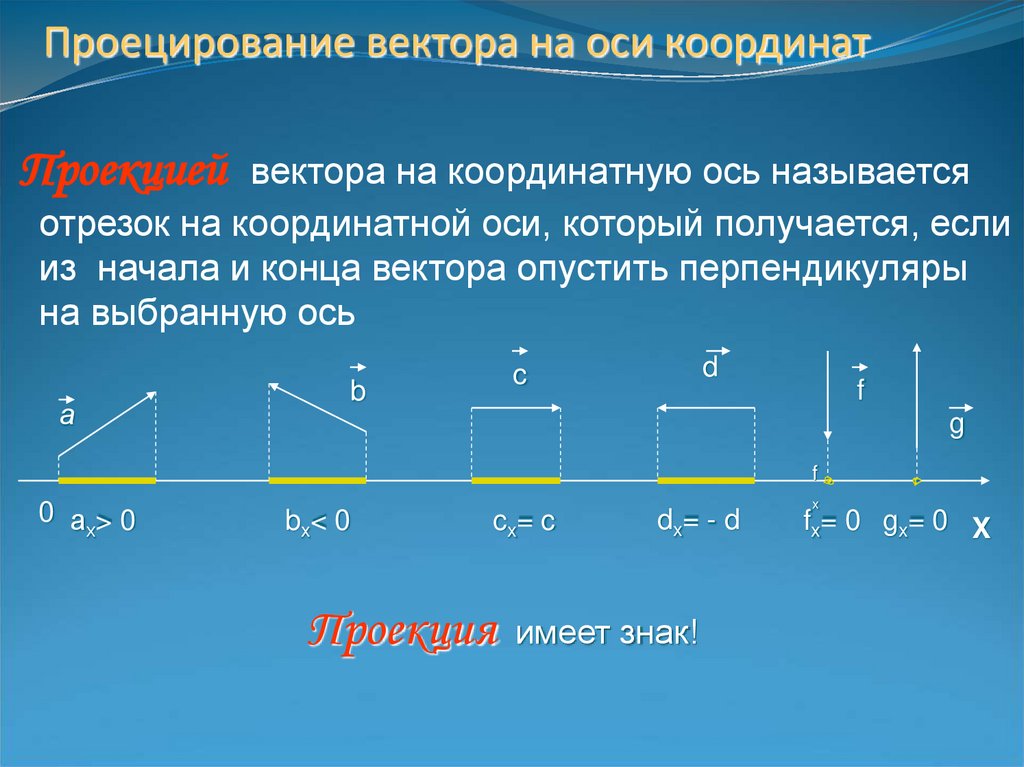
10. Проецирование вектора на оси координат

Проекцией вектора на координатную ось называется
отрезок на координатной оси, который получается, если
из начала и конца вектора опустить перпендикуляры
на выбранную ось
b
а
d
c
f
g
f
0 а>0
х
bx< 0
cx= c
dx= - d
Проекция имеет знак!
x
fx= 0 gx= 0 X

11. Проекция вектора на взаимно перпендикулярные оси

Y
аY
O
а
ax
a=√ax2+ay2
tgφ=ay/ax
ау=a·sinφ
ах=а·cosφ
X

12. Проекция суммы векторов (проекция разности векторов)

a+b=c
cx= ax + bx = a·cosα+ b·cosβ
cy= ay + by = a·sinα + b·sinβ
c = √cx2 + cy2
tgγ =cy/cx