Понятие функции. Функциональная зависимость

1.

§21. Понятие функции
п.1. Функциональная зависимость.
X ,Y R
Соответствие f, которое каждому элементу
x X сопоставляет единственный элемент
y Y , называют функцией.
y f (x )
f :X Y

2.

x
f
y
X
E
Y
X D ( y ) ─ область определения
E ( y ) { y Y : y f ( x ), x X } ─ множество
а значений

3.

Способы задания функции.
1) Аналитический способ.
y x
2
2) Табличный способ.
x
0
1
2
3
y
1
4
9
3) Графический способ.
y
0
O
x

4.

Основные характеристики функций
1) Четность (нечетность).
Функция y f (x ),определенная на множестве
D, называется четной (нечетной),
если x D выполняются условия:
x D,
f ( x) f ( x)
f ( x) f ( x) .

5.

y
y
x
O
четная функция
O
нечетная функция
Самостоятельно: привести по 2 примера
четных, нечетных функций и функций, не
являющихся ни четными, ни нечетными.
x

6.

2) Монотонность.
Функция y f (x ) определенная на множестве
D, называется строго возрастающей
(строго убывающей) на множестве I D ,
если
x1 , x2 I : x1 x2
f ( x1 ) f ( x2 )
f ( x1 ) f ( x2 )
Строго возрастающие
Строго убывающие
Строго монотонные функции

7.

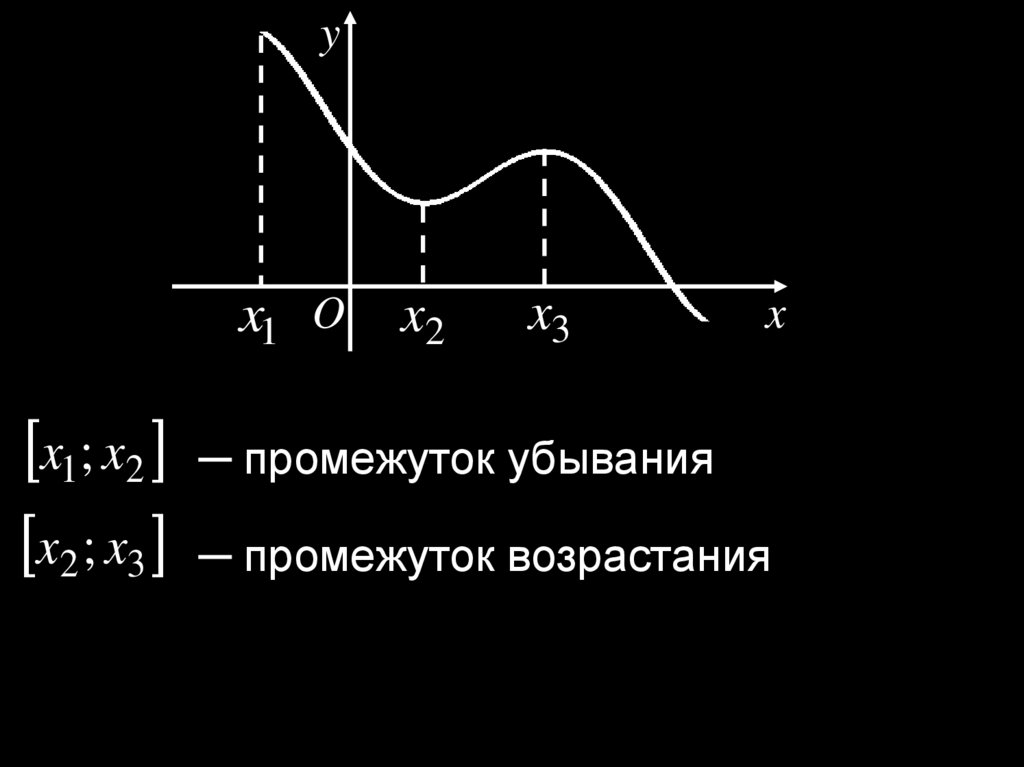
y
x1 O
x2
x3
x
x1; x2 ─ промежуток убывания
x2 ; x3 ─ промежуток возрастания

8.

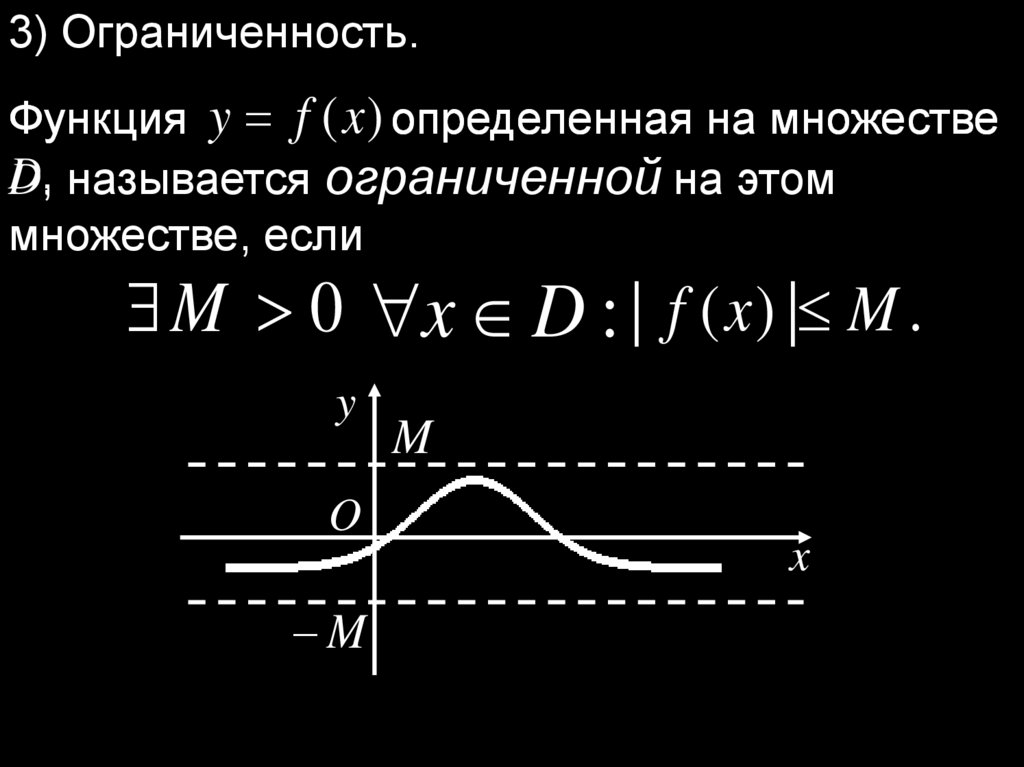
3) Ограниченность.
Функция y f (x ) определенная на множестве
D, называется ограниченной на этом
множестве, если
M 0 x D : | f ( x ) | M .
y
O
M
M
x

9.

4) Периодичность.
Функция y f (x ) определенная на множестве
множестве
D, называется периодической на этом
множестве, если
T 0 x D : ( x T ) D
f ( x T ) f ( x ).
T ─ период

10.

п.2. Понятие обратной и сложной
функции.
x
f
f :D E
1
Соответствие f ,
f 1
y которое каждому
элементу y E ,
E
D
сопоставляет
единственный элемент x D такой, что
f ( x ) y , называют функцией, обратной к
функции f.

11.

y
O
y x
y x , y : [0;3] [0;9]
2
y x , y : [0;9] [0;3]
x
Самостоятельно: привести еще 2 примера с
геометрический интерпретацией.

12.

X
y
f
x
g
z
Z
элемент z Z
f :X Y
y f (x )
Y g :Y Z
z g ( y)
Соответствие , которое
каждому элементу x X
сопоставляет единственный
такой, что
z ((xx ) g ( f ( x )),
называют сложной функцией, или
суперпозицией (композицией) функций f и g.

13.

Пример.
f ( x ) sin x
g ( x) e
x
( x ) g ( f ( x )) e
x
( x ) f ( g ( x )) sin e
sin x
Самостоятельно: привести еще 2 примера.