Похожие презентации:
Преобразование подобия. Свойства преобразования подобия
1.
Преобразованиеподобия.
Свойства
преобразования
подобия.
2.
Повторение.Преобразование одной фигуры в другую
называется движением, если оно сохраняет
расстояние между точками.
F1
X1
Y1
XY = X1Y1
3.
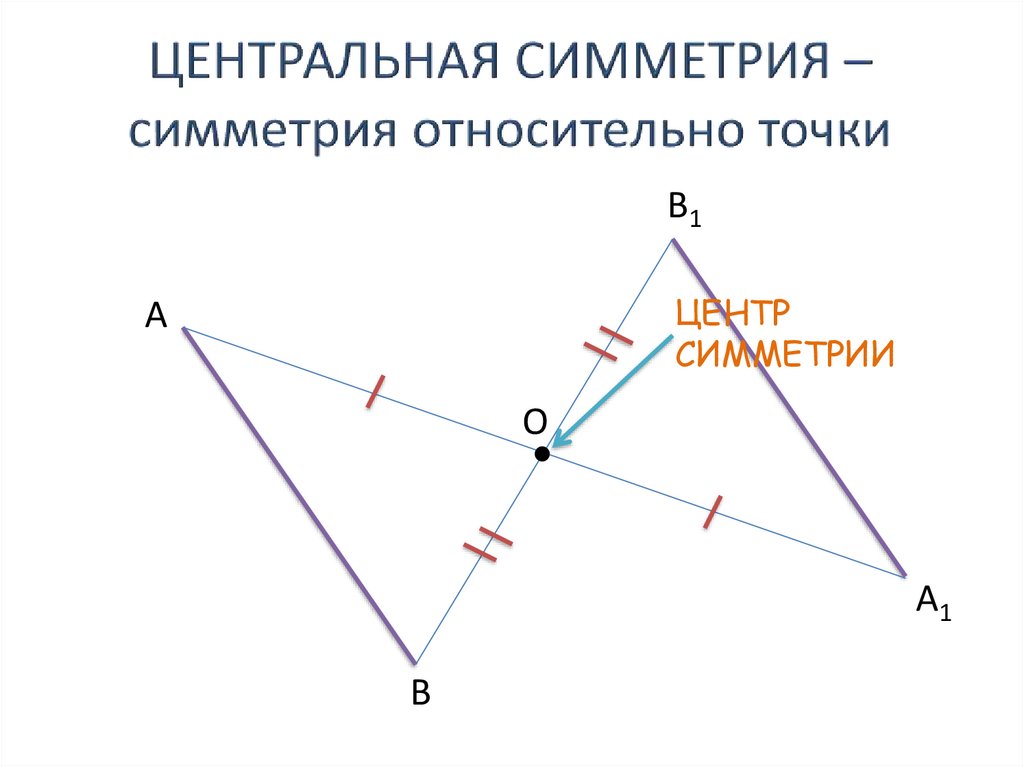
ЦЕНТРАЛЬНАЯСИММЕТРИЯ
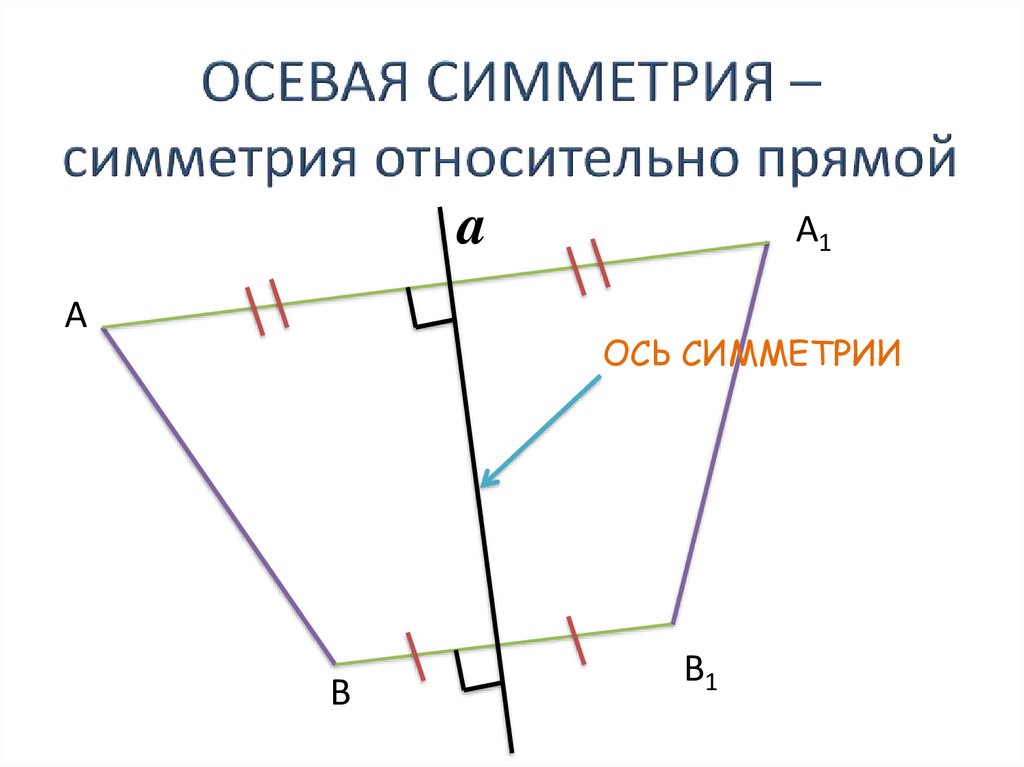
ОСЕВАЯ СИММЕТРИЯ
ПОВОРОТ
ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС
4.
В1ЦЕНТР
СИММЕТРИИ
А
О
А1
В
5.
aА
А1
ОСЬ СИММЕТРИИ
В
В1
6.
УГОЛПОВОРОТА
А
1
А
НАПРАВЛЕНИЕ
ПОВОРОТА:
ИЛИ
В1
В
ЦЕНТР
ПОВОРОТА
О
7.
А1А
ВЕКТОР
ПЕРЕНОСА
В1
В
8.
Все ли представленные здесь преобразованияявляются движениями?
9.
Преобразование подобия и его простейшие свойства.10.
Преобразование подобия и его простейшие свойства.Подобие в природе.
11.
Преобразование подобия и его простейшие свойства.12.
Преобразование подобия и его простейшие свойства.Преобразование фигуры F в фигуру F′
называется преобразованием подобия, если
при этом преобразовании расстояние между
точками изменяется в одно и то же число раз.
F′ = kF
k – коэффициент
подобия.
13.
Преобразование подобия и его простейшие свойства.Определите коэффициент
подобия.
При k = 1
преобразование подобия
является
движением.
14.
F – данная фигура,О – фиксированная точка
Пусть k = 2
коэффициент
гомотЕтии
F′
F
Преобразование фигуры F,
при котором каждая её точка Х
переходит в точку Х′, построенную
указанным способом, называется
гомотЕтией относительно
центра О.
(гомотЕтия (греч.) –
одинаково расположенный)
Фигуры F и F′ называют
гомотетичными.
Т ГомотЕтия есть
преобразование подобия.
O – центр гомотЕтии
15.
Преобразование подобия и его простейшие свойства.• Преобразование подобия переводит
прямые в прямые, полупрямые в
полупрямые, отрезки в отрезки.
• Преобразование подобия сохраняет углы
между полупрямыми.
16.
Задача.• Постройте отрезок (треугольник),
гомотетичный данному относительно
центра О с коэффициентом к = 1,5 (к = 0,5).
17.
Итог урока.1. Что такое преобразование подобия?
2. Что такое гомотетия, центр гомотетии,
коэффициент гомотетии?
3. Чем является гомотетия?
4. Какие свойства преобразования подобия вам
известны?















 Математика
Математика








